Object Detection.
目标检测(Object Detection)任务是指在图像中检测出可能存在的目标;包括定位和分类两个子任务:其中定位是指确定目标在图像中的具体位置,分类是确定目标的具体类别。
本文目录:
1. 传统的目标检测算法
传统的目标检测算法主要有三个步骤,
- 在图像中生成候选区域(proposal region);
- 对每个候选区域提取特征向量,这一步通常是用人工精心设计的特征描述子(feature descriptor)提取图像的特征;
- 对每个候选区域提取的特征进行分类,确定对应的类别。
(1)生成候选区域
常用的候选区域生成方法包括滑动窗口、Felzenszwalb算法、选择搜索算法。
⚪ 滑动窗口 Sliding Window
候选区域通常是由滑动窗口实现的;结合不同尺度的图像以及不同尺度的窗口可生成大量的候选区域。
⚪ Felzenszwalb算法
Felzenszwalb算法通过基于图的方法把图像分割成一些相似的区域。使用无向图$G=(V,E)$表示输入图像,其中的一个节点$v_i \in V$代表一个像素,一条边$e_{ij} = (v_i,v_j) \in V$连接两个节点$i,j$,每条边$e_{ij}$有一个权重$w_{ij}$衡量两个节点$i,j$的不相似程度(可以通过颜色、位置、强度值来衡量)。则一个分割结果$S$是把节点$V$分配到多个内部相互连接的子集\(\{C\}\)中。相似的像素应该属于通过一个子集,不相似的像素被分配到不同的子集。
构造一个图像的图的方法有两种:
- 网格图 (Grid Graph):每个像素只和其邻域内的像素连接(比如周围的$8$个像素),边的连接权重是像素的强度值之差的绝对值。
- 最近邻图 (Nearest Neighbor Graph):把每个像素表示为位置+颜色特征空间中的一个点$(x,y,r,g,b)$,两个像素之间的边权重是像素特征向量的欧氏距离。
首先定义以下几个概念:
- 内部差异 (Internal difference):$Int(C)=\max_{e \in MST(C,E)} w(e)$。其中MST表示最小生成树。当移除所有权重小于$Int(C)$的边时,集合$C$仍然保持连接。
- 两个集合之间的差异 (difference):$Diff(C_1,C_2)=\min_{v_i\in C_1,v_j \in C_2,(v_i,v_j) \in E} w(v_i,v_j)$。若两个集合之间没有边连接,则定义$Diff(C_1,C_2)=\infty$。
- 最小内部差异 (Minimum internal difference):$MInt(C_1,C_2)=\min(Int(C_1)+k/|C_1|,Int(C_2)+k/|C_2|)$。阈值$k$越大则则倾向于选择较大的子集。
给定两个区域$C_1,C_2$,则当下列判据成立时才把这两个区域视为两个独立的子集;否则分割过于细致,应该把两个区域合并。
\[D(C_1,C_2) = \begin{cases} True & Diff(C_1,C_2) > MInt(C_1,C_2) \\ False & Diff(C_1,C_2) \leq MInt(C_1,C_2) \end{cases}\]Felzenszwalb算法采用自底向上的处理流程。给定具有$|V|=n$个节点和$|E|=m$条边的无向图$G=(V,E)$:
- 把边按照权重升序排列$e_1,e_2,…,e_m$;
- 初始化时把每个像素看作一个单独的区域,则一共有$n$个区域;
- 重复以下操作$k=1,…,m$:
- 第$k-1$步的分割结果为$S^{k-1}$;
- 选取排序后的第$k$条边$e_k=(v_i,v_j)$;
- 如果$v_i,v_j$在分割$S^{k-1}$中属于同一个区域,则直接令$S^k=S^{k-1}$;
- 如果$v_i,v_j$在分割$S^{k-1}$中属于不同的区域$C_i^{k-1},C_j^{k-1}$,若$w(v_i,v_j) \leq MInt(C_i^{k-1},C_j^{k-1})$则将两个区域合并;否则不做处理。
import scipy
import skimage.segmentation
img = scipy.misc.imread("image.jpg", mode="L")
segment_mask = skimage.segmentation.felzenszwalb(img, scale=100)
⚪ 选择搜索算法 Selective Search
选择搜索算法是一种常用的提取潜在目标的区域提议算法。该算法建立在图像分割结果上(如Felzenszwalb算法的输出),并使用基于区域的特征执行自底向上的层次划合并。选择搜索算法的工作流程如下:
- 初始化阶段,使用Felzenszwalb算法生成图像的分割区域集合;
- 使用贪心算法迭代地执行区域合并:
- 首先计算所有相邻区域之间的相似度;
- 两个最相似的区域被合并为一组,然后计算新的区域和其邻域区域之间的相似度。
- 重复执行相似区域之间的合并,直至整个图像变成单个区域。
- 上述过程中产生的所有区域都被视为可能存在目标的区域。
在评估两个区域之间的相似性时,采用四种互补的相似性度量:
- 颜色
- 纹理:通过SIFT算子提取特征
- 尺寸:鼓励较小的区域尽早合并
- 形状:理想情况下,一个区域可以填补另一个区域的空白
通过调整Felzenszwalb算法的阈值$k$、改变颜色空间、选择不同的相似性度量组合,可以制定一套多样化的选择搜索策略。能够产生具有最高质量的提议区域的选择搜索策略为:不同初始分割结果的混合+多种颜色空间的混合+所有相似性度量的组合。算法也需要在质量(模型复杂性)和速度之间取得平衡。
(2)设计特征描述子
常用的特征描述子包括图像梯度向量、方向梯度直方图HOG、尺度不变特征变换SIFT、可变形部位模型DPM。
⚪ 图像梯度向量 Image Gradient Vector
图像梯度向量定义为每个像素沿着$x$轴和$y$轴的像素颜色变化度量。若$f(x,y)$表示像素位置$(x,y)$处的颜色,则像素$(x,y)$的梯度向量定义为:
\[\nabla f(x,y) = \begin{bmatrix} g_x \\ g_y \end{bmatrix}= \begin{bmatrix} \frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y} \end{bmatrix}= \begin{bmatrix} f(x+1,y)-f(x-1,y) \\ f(x,y+1)-f(x,y-1) \end{bmatrix}\]梯度向量的幅值(magnitude) $g$定义为向量的L2范数;梯度向量的方向(direction) $\theta$定义为两个偏导数方向之间的夹角。
\[g = \sqrt{g_x^2+g_y^2}, \quad \theta = \arctan(\frac{g_y}{g_x})\]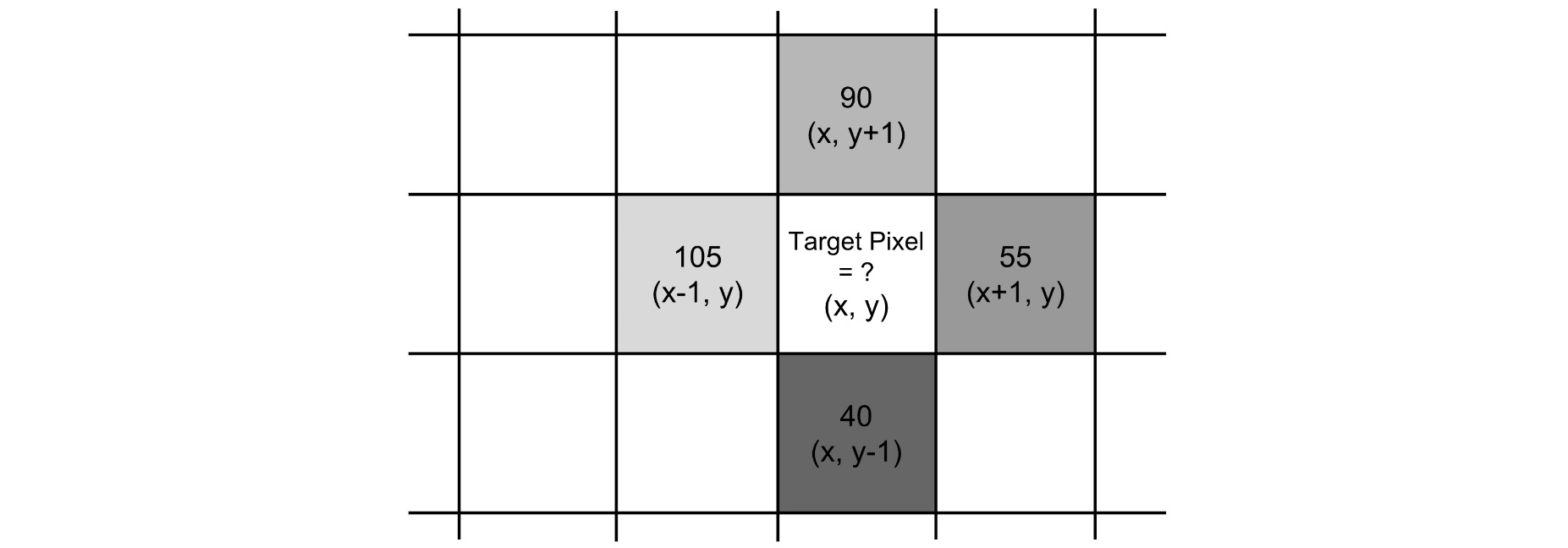
如上图中像素$(x,y)$的梯度向量为:
\[\nabla f = \begin{bmatrix} f(x+1,y)-f(x-1,y) \\ f(x,y+1)-f(x,y-1) \end{bmatrix} = \begin{bmatrix} 55-105 \\ 90-40 \end{bmatrix} = \begin{bmatrix} -50 \\ 50 \end{bmatrix}\]⚪ 方向梯度直方图 Histogram of Oriented Gradients
方向梯度直方图 (HOG) 的构造过程如下:
- 预处理图像,包括尺寸调整和像素值归一化;
- 计算每个像素的梯度向量,并进一步计算其幅值和方向;
- 把图像划分成一系列$8\times 8$的图像块。对于每个图像块,把其中$64$个像素梯度向量的幅值累加到直方图的$9$个桶中,直方图根据梯度向量的方向绝对值($0-180°$)经验性地划分成$9$个均匀的桶;
- 如果一个像素的梯度向量的方向恰好位于两个桶之间,则将其按比例划分到两个桶中;比如大小为$8$的梯度向量方向为$15°$,则分别把$6$和$2$划分到$0°$桶和$20°$桶中;这种分配方式对图像较小的失真具有鲁棒性;
- 在图像上滑动$2\times 2$个图像块(对应$16\times 16$像素)。每个滑动窗口中的$4$个直方图被连接后进行归一化。最终的HOG特征向量是所有滑动窗口向量的级联。
- HOG特征向量可以被输入到分类器中,用于学习目标识别任务。

⚪ 尺度不变特征变换 Scale Invariant Feature Transform
尺度不变特征变换 (SIFT)是一种非常稳定的局部特征,具有旋转不变性、尺度不变性、亮度变化保持不变性。SIFT特征的构造过程如下:
- DoG尺度空间的极值检测:为了使算子具有尺度不变性,先构造高斯差分尺度空间 (Difference of Gaussina, DOG):通过不同$\sigma$值的高斯滤波和降采样构造图像的高斯尺度空间,再通过每组高斯空间中的相邻图像相减得到DoG图像。对于DoG中的每个像素点,将其与所在图像$3×3$邻域$8$个像素点以及同一尺度空间中上下两层图像$3×3$邻域$18$个像素点进行比较。当其值大于(或者小于)所有比较点时,该点为候选极值点;

- 删除不稳定的极值点:对DoG尺度空间函数进行二次泰勒展开求极值点,去掉局部曲率非常不对称的点。剔除的点主要有两种:低对比度的特征点和不稳定的边缘响应点;
- 确定特征点的主方向:计算以特征点为中心的邻域内各个像素点的HOG直方图(以$45°$划分直方图,则共有$8$个桶),直方图中最高峰所对应的方向即为特征点的方向。

- 生成特征点的描述子:为了使算子具有旋转不变性,首先将坐标轴旋转为特征点的方向。以特征点为中心划分$4×4$的图像块,每个图像块包括$4×4$像素。对每个图像块构造HOG直方图(长度为$8$的向量),一个特征点可以产生$128$维的SIFT特征向量。为了使算子具有亮度变化保持不变性,对SIFT特征向量进行归一化处理。
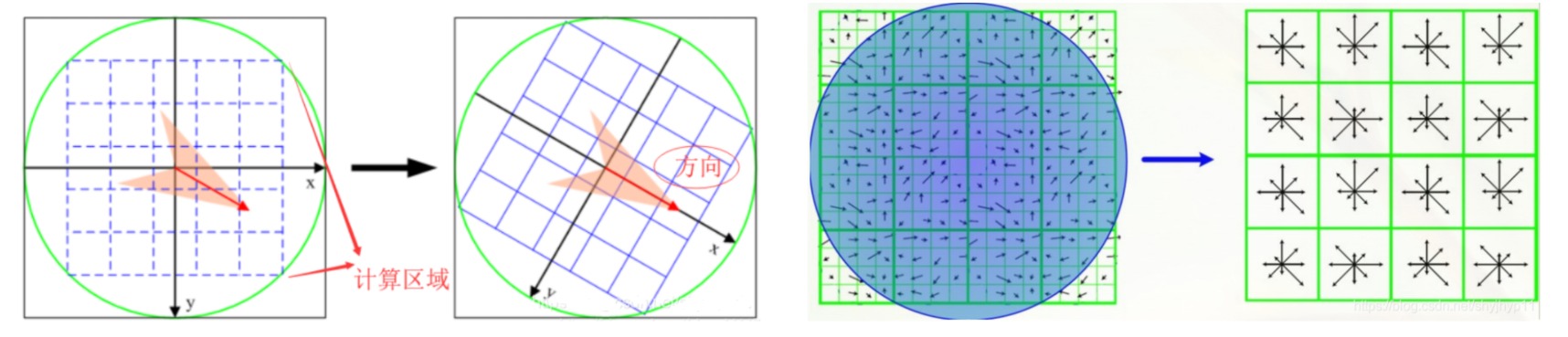
⚪ Deformable Parts Model (DPM)
可变形部位模型(DPM)使用可变形部位的混合图模型(马尔可夫随机场)来识别目标。DPM主要由三个部分组成:
- 一个根滤波器(root filter)近似定义覆盖整个目标的检测窗口,并指定区域特征向量的权重;
- 多个部位滤波器(part filter)覆盖目标的较小部位,其学习分辨率设置为根滤波器的两倍。
- 一个空间模型(spatial model)对部位滤波器相对于根滤波器的位置进行评分。

检测目标的质量是通过滤波器的得分减去变形成本来衡量的。令$x$为输入图像,$y$是$x$的一个子区域,$\beta_{root},\beta_{part}$分别代表根滤波器和部位滤波器,代价函数$cost()$衡量部位偏离其相对于根的理想位置的惩罚。则模型匹配图像$x$的得分$f()$计算为:
\[f(model, x) = f(\beta_{root},x) + \sum_{\beta_{part}} \max_y [f(\beta_{part},y)-cost(\beta_{part},x,y)]\]得分模型$f()$通常设置为滤波器$\beta$与区域特征向量$\Phi(x)$的点积:$f(\beta,x) = \beta\cdot \Phi(x)$。区域特征向量$\Phi(x)$可以由HOG算子构造。根滤波器中得分较高的位置检测出包含目标可能性高的区域,而部位滤波器中得分较高的位置证实了已识别的物体假设。
2. 基于深度学习的目标检测模型
在传统的方法中,经常会使用集成、串联学习、梯度提升等方法来提高目标检测的准确率;但是传统的方法逐渐暴露出很多问题,比如检测准确率有限、需要人工设计特征描述子等。近些年来深度学习的引入使得目标检测的精度和速度有了很大的提升,卷积神经网络能够提取图像的深层语义特征,省去了人工设计和提取特征的步骤。
目前主流的目标检测模型分成两类。
- 两阶段(Two-Stage)的目标检测模型:首先在图像中生成可能存在目标的候选区域,然后对这些候选区域进行预测。这些方法精度高,速度相对慢一些;
- 单阶段(One-Stage)的目标检测模型:把图像中的每一个位置看作潜在的候选区域,直接进行预测。这些方法速度快,精度相对低一些。

上图是目前大部分目标检测模型的主要流程图。一个目标检测系统主要分成三部分,如图中的backbone、neck和regression部分。
- backbone部分通常是一个卷积网络,把图像转化成对应的特征映射(feature map);
- neck部分通常是对特征映射做进一步的增强处理;
- regression部分通常把提取的特征映射转换成边界框(bounding box)和类别(class)信息。
单阶段的目标检测模型直接在最后的特征映射上进行预测;而两阶段的方法先在特征映射上生成若干候选区域,再对候选区域进行预测。由此可以看出单阶段的方法所处理的候选区域是密集的;而两阶段的方法由于预先筛选了候选区域,最终处理的候选区域相对来说是稀疏的。
下面介绍一些常用的目标检测模型:
- 两阶段的目标检测模型:R-CNN, Fast RCNN, Faster RCNN, SPP-Net, FPN, Libra RCNN, Cascade RCNN, Sparse RCNN
- 单阶段的目标检测模型:OverFeat, YOLOv1-3, SSD, RetinaNet, Guided Anchoring, ASFF, EfficientDet, YOLT, Poly-YOLO, YOLOv4, YOLOv5, RTMDet
- Anchor-Free的目标检测模型:(anchor-point方法) FCOS, YOLOX, YOLOv6, YOLOv7, YOLOv8, YOLOv9, YOLOv10; (key-point方法) CornerNet, CenterNet, RepPoints
- 基于Transformer的目标检测模型:DETR, Deformable DETR
⭐ 扩展阅读
- Recent Advances in Deep Learning for Object Detection:(arXiv1908)深度学习中目标检测最近的进展综述。
- MMDetection: Open MMLab Detection Toolbox and Benchmark:商汤科技和香港中文大学开源的基于Pytorch实现的深度学习目标检测工具箱。
(1)两阶段的目标检测模型
⚪ R-CNN
R-CNN首先应用选择搜索算法提取感兴趣区域,对于每个区域进行尺寸调整后通过预训练的卷积神经网络提取特征向量,并通过二元支持向量机对每个预测类别进行二分类。为进一步提高检测框的定位精度,训练一个回归器进行边界框的位置和尺寸修正。

⚪ Fast R-CNN
- paper:Fast R-CNN
Fast R-CNN是对R-CNN的改进:
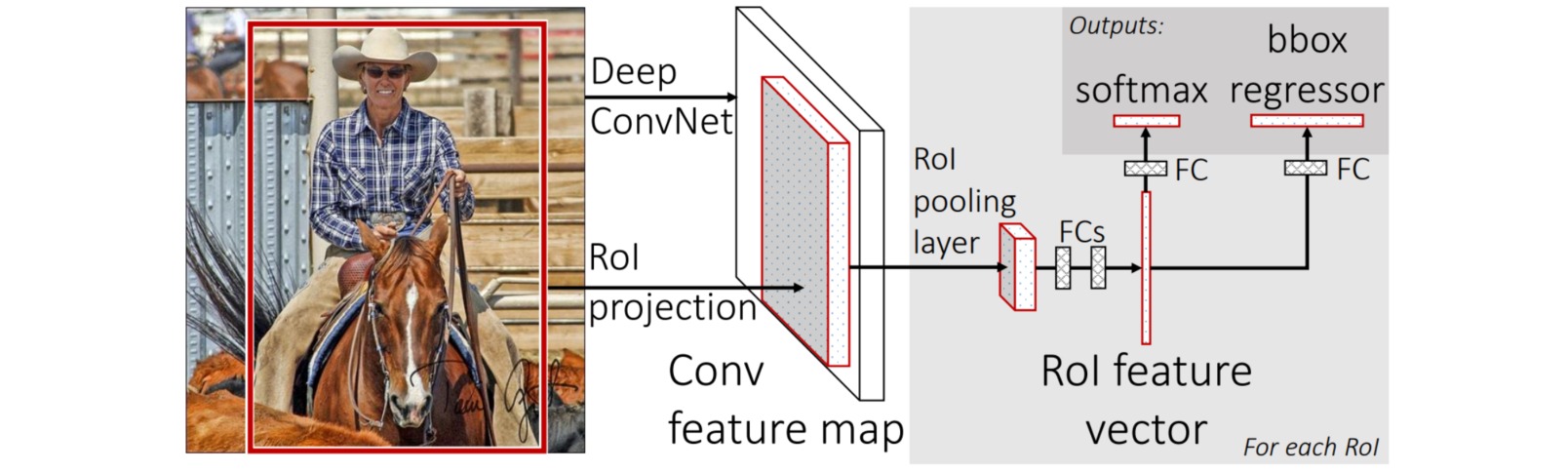
- Fast R-CNN首先将图像通过卷积网络提取特征映射,在原始图像中生成的候选区域被投影到在特征映射的对应位置;
- Fast R-CNN把特征区域的各向异性放缩替换为RoI Pooling层,即通过最大池化把候选区域的特征映射转换成固定尺寸的特征。
- Fast R-CNN把用于目标分类的分类损失和用于目标边界框坐标修正的回归损失结合起来一起训练。
⚪ Faster R-CNN
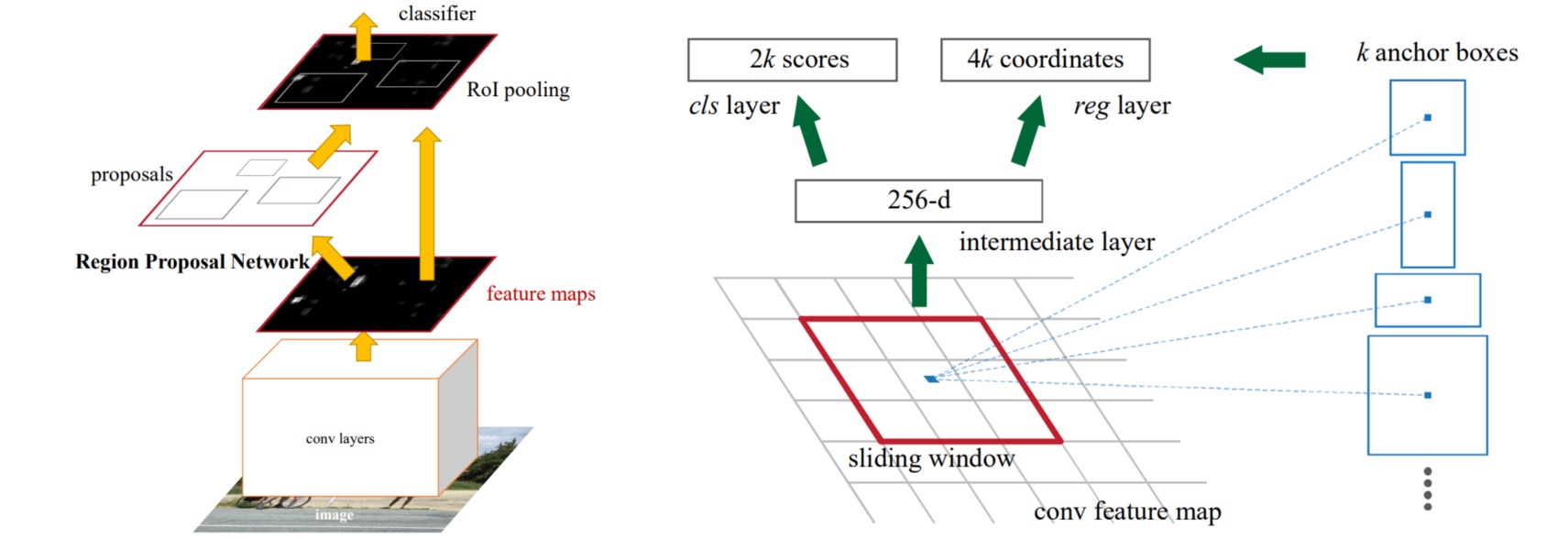
Faster R-CNN改进了R-CNN和Fast RCNN中的候选区域生成方法,使用区域提议网络(Region Proposal Network, RPN)代替了选择搜索算法。RPN在预训练卷积网络输出特征映射每个元素对应的输入像素位置预设一系列具有不同尺寸和长宽比的anchor,并进行anchor分类和边界框回归;只有正类anchor被视为可能存在目标的proposals,并通过RoI Pooling和预测头执行目标分类和目标边界框坐标修正。
⚪ SPP-Net
在目标检测模型中需要把尺寸和形状各异的proposal调整到固定的尺寸以进行后续的分类和边界框回归任务。SPP-Net提出了一种空间金字塔池化(Spatial Pyramid Pooling, SPP)层,能够把任意不同尺寸和不同长宽比的图像特征转换为固定尺寸大小的输出特征向量。在实现时分别把特征划分成$k_i \times k_i$的栅格,然后应用最大池化操作构造长度为$\sum_i k_i^2c$的输出特征。

⚪ FPN
卷积网络不同层输出的特征映射具有不同的感受野和分辨率,适合检测不同尺度的目标:浅层特征具有较高的分辨率,适合检测小目标;深层特征具有范围较大的感受野,适合检测大目标。
特征金字塔网络 (Feature Pyramid Network, FPN)通过转置卷积和特征融合生成不同尺度的特征,并在这些空间信息和语义信息都很丰富的特征映射上同时执行目标检测任务。

⚪ Libra R-CNN
Libra R-CNN出发点为解决目标检测中的一些不均衡现象,如采样不均衡、不同阶段特征分布的不均衡、框回归过程中不均衡。改进包括IoU均衡采样,对FPN结构的均衡以及对L1 loss的均衡:

⚪ Cascade R-CNN
在Faster R-CNN等网络中,在训练时会为RPN网络设置IoU阈值,以区分proposal是否包含目标,进而只对positive proposal进行边界框回归;通常该阈值设置越高,生成的proposal越准确,但是正样本的数量降低,容易过拟合。而在推理时所有proposal都用于边界框回归。这导致这导致了在训练和测试阶段中,proposal的分布不匹配问题。
为了提高检测精度,产生更高质量的proposal,Cascade R-CNN使用不同IoU阈值($0.5$、$0.6$、$0.7$)训练多个级联的检测器,通过串联的学习获得较高的目标检测精度。

⚪ Sparse R-CNN
Sparse RCNN通过嵌入指定的$N$个可学习候选框Proposal Boxes来提供RoI坐标,通过嵌入指定的$N$个可学习实例级别特征Proposal Features来提供更多的物体相关信息;并采用级联思想对输出的bbox进行refine。
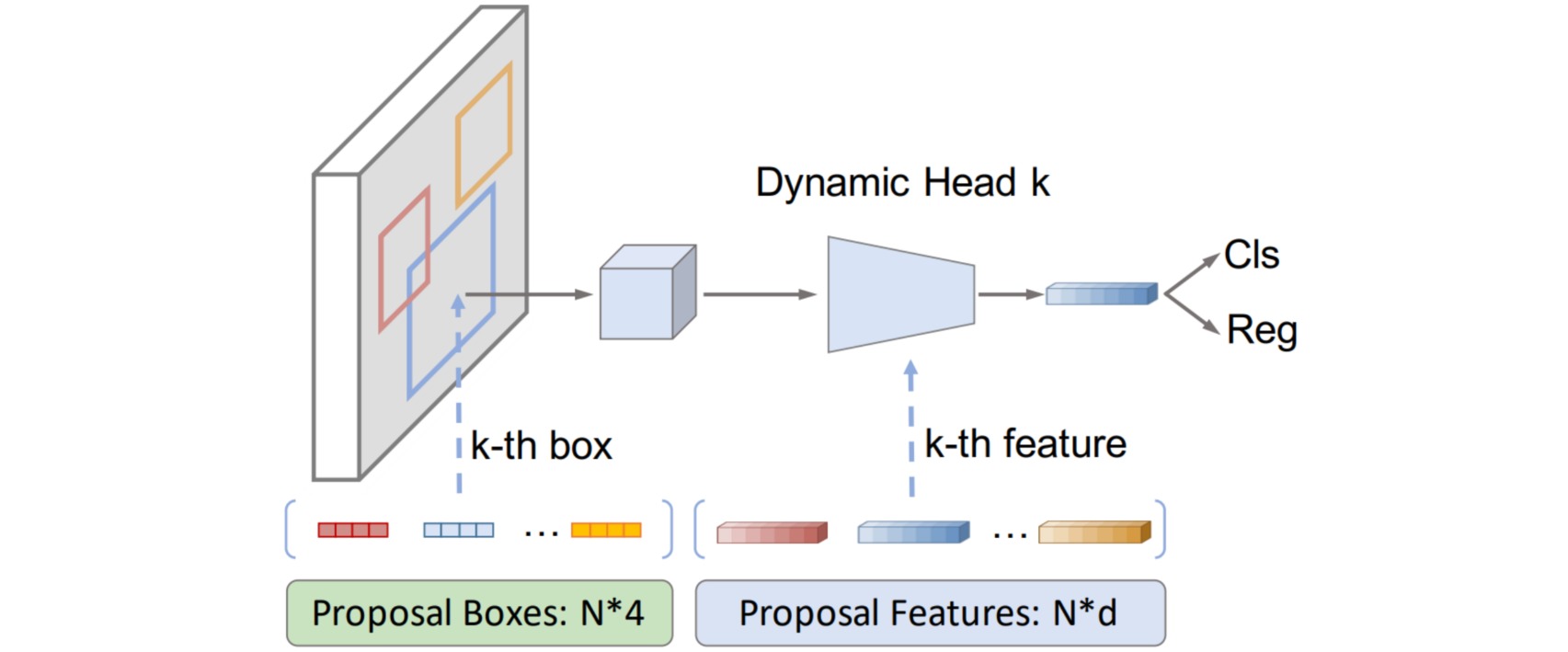
(2)单阶段的目标检测模型
⚪ OverFeat
OverFeat使用同一个卷积神经网络同时执行目标检测、定位和分类任务,其主要思想是:构建一个卷积神经网络(采用AlexNet结构:作为特征提取器的全卷积网络+作为分类器的全连接层),以滑动窗口的方式在不同尺度的图像的不同区域位置上进行图像分类,然后通过把分类器调整为回归器进行边界框位置预测。
OverFeat的训练流程:
- 在图像分类任务上训练卷积神经网络;
- 冻结特征提取器,把分类器替换为回归器,在每个空间位置和尺度上预测每个类别边界框的坐标$(x_{left},x_{right},y_{top},y_{bottom})$。
OverFeat的检测流程:
- 使用预训练的卷积网络在每个位置上执行分类;
- 对于生成的所有已分类区域预测目标边界框;
- 合并重叠的边界框以及可能来自同一个目标的边界框。
注意到全卷积网络可以并行地以滑动窗口的方式提取图像特征。OverFeat采用$5\times 5$卷积核实现滑动窗口,相当于在输入图像上设置$14 \times 14$的窗口。

⚪ YOLO
YOLO模型把图像划分成$S\times S$个网格(对应尺寸为$S\times S$的特征映射),每个网格预测$B$个边界框的坐标和置信度得分,以及当边界框中存在目标时的$K$个类别概率。网络的输出特征尺寸为$S\times S \times (5B+K)$。

⚪ YOLOv2/YOLO9000
YOLOv2相比于YOLO进行以下改进:
- 网络结构的改进:增加BatchNorm、引入跳跃连接、轻量级网络
- 检测方式的改进:引入anchor、通过k-means设置anchor
- 训练过程的改进:增大图像分辨率、多尺度训练
YOLO9000结合小型目标检测数据集(COCO的$80$类)与大型图像分类数据集(ImageNet的前$9000$类)联合训练目标检测模型。如果输入图像来自分类数据集,则只会计算分类损失。
⚪ YOLOv3
YOLOv3相比于YOLOv2进行以下改进:
- 网络结构的改进:特征提取网络为DarkNet53、使用多层映射进行多尺度检测、构造特征金字塔网络增强特征
- 损失函数的改进:边界框回归损失采用GIoU损失、置信度分类与类别分类损失采用二元交叉熵
⚪ SSD
SSD模型提取包含不同尺度的图像的特征金字塔表示,并在每个尺度上执行目标检测。在每一层特征映射上,SSD设置不同尺寸的anchor来检测不同尺度的目标。对于每一个特征位置,模型对$k=6$个anchor分别预测$4$个边界框位置偏移量与$c$个类别概率。则对于$m\times n$的特征图,模型输出特征尺寸为$m\times n\times k(c+4)$。

⚪ RetinaNet
RetinaNet的两个关键组成部分是Focal Loss和特征图像金字塔。Focal Loss用于缓解边界框的正负样本类别不平衡问题;特征图像金字塔通过FPN构造多尺度特征进行预测。

⚪ Guided Anchoring
Guided Anchoring把回归anchor分支替换为两条预测分支,一条分支用于区分前后景,目标是预测哪些区域应该作为中心点来生成 anchor;另一条分支是用于预测anchor的长和宽。
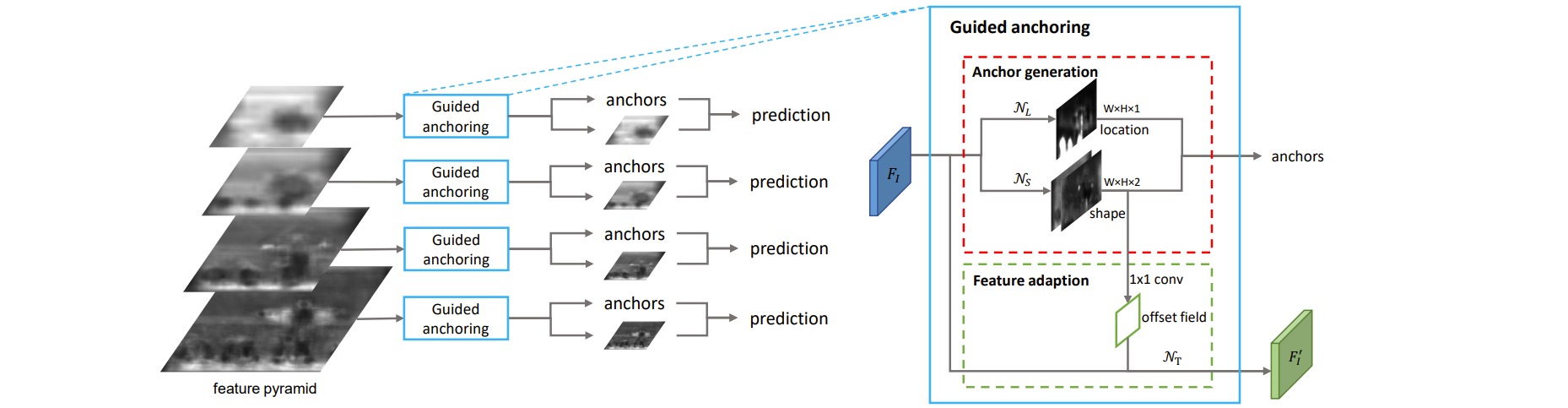
⚪ Adaptively Spatial Feature Fusion (ASFF)
ASFF通过可学习的权重把FPN中具有不同语义信息的特征图进行自适应融合。

⚪ EfficientDet
EfficientDet提出了BiFPN和联合缩放方法(Compound Scaling)。BiFPN在特征融合前为每一个特征设置了一个权重系数 $\phi$,并引入了跨尺度连接;联合缩放方法对目标检测网络的BackBone的输出分辨率、宽度和深度、BiFPN(Neck)的深度和宽度、预测网络(Head)的宽度和深度同时缩放。

⚪ YOLT
对于高分辨率大尺寸图像(如遥感图像)中的目标检测问题,YOLT提出了一种两阶段的检测框架:首先把输入图像划分成重叠的子图像,对每张子图像分别进行检测;再通过全局的非极大值抑制算法获得最终的检测结果。

⚪ Poly-YOLO
YOLOv3由于特殊的网格预测模式,当物体比较密集且大小差不多时,会存在标签重写现象;并且在该场景下基于kmeans计算得到的anchor会出现物体预测尺度和感受野不符的问题。
针对上述问题,Poly-YOLO提出采用单尺度预测,且维持高输出分辨率特征图的策略。为了进一步提高性能,采用了通道注意力单元、hypercolumn + stairstep上采样特征聚合方式来加强特征提取能力。

⚪ YOLOv4
YOLOv4相比于之前YOLO系列的改进包括:
- 网络结构的改进:backbone采用CSPDarkNet53、neck采用SPP+PANet
- 训练过程的改进:回归损失采用CIoU Loss、引入标签平滑、引入Mosaic数据增强
⚪ YOLOv5
YOLOv5相比于之前YOLO系列的改进包括:
- 网络结构的改进:CSPDarknet + PAFPN + 非解耦 Head
- 标签分配策略:采用了 anchor 和 gt_bbox 的形状匹配度作为划分规则,同时引入跨邻域网格策略来增加正样本
- 训练和推理的改进:采用Mosaic + RandomAffine + MixUp数据增强、推理时引入 batch shape 策略
⚪ RTMDet
MMDetection 核心开发者针对当前 YOLO 系列的诸多改进模型进行了经验性的总结,推出了高精度、低延时的单阶段目标检测器 RTMDet。
- 模型结构:整体结构由 CSPNeXt + CSPNeXtPAFPN + 共享卷积权重但分别计算 BN 的 SepBNHead 构成。内部核心模块是 CSPNeXt Block。
- 标签分配策略:Dynamic Soft Label Assigner,该方法主要包括使用位置先验信息损失、样本回归损失、样本分类损失,同时对三个损失进行了 Soft 处理进行参数调优。
- 损失函数:分类损失采用QualityFocalLoss,回归损失采用GIoULoss。
(3) Anchor-Free的目标检测方法
目标检测模型的主流是Anchor-Based的方法。这种方法在特征图的每一个像素点预设几个不同尺度和长宽比的边界框,称之为anchor。网络对每一个 anchor 进行分类,并对正类的 anchor 进行回归(位置及大小调整)。这类方法的主要优点是:
- 很大程度上减少了计算量,并将 proposal 数量放到可控范围内以便后面的计算和筛选;
- 通过调整不同的 anchor 设置可以覆盖尽可能多的物体,也可针对不同任务设置不同的 anchor 尺度范围;
- 由于 anchor 的尺度是人工定义的,物体的定位是通过 anchor 的回归来实现,通过计算偏移量而不是物体的位置大大降低了优化难度。
然而 anchor 的设置也有着它自身的缺点。单纯通过使用更多不同大小和长宽比的 anchor 以及更多的训练技巧就可以达到更好的效果,然而这种通过增加算力而改进网络的方法很难落实到实际的应用中。并且 anchor 的设定需要人为设定大量的参数,且离散的 anchor 尺度设定会导致一些物体无法很好的匹配,从而导致遗漏。
Anchor-Free的目标检测方法没有采用“预设anchor+偏移量回归”的检测流程,而是把目标检测任务视作关键点检测等其它形式的任务,直接对目标的位置进行预测;可分为Anchor-Point检测和Key-Point检测。
- Anchor-Point检测器:根据中心点到检测框边界的距离将目标bboxes编码为anchor point,表现为特征图上的一个像素,关联着当前位置的特征。这类方法能够灵活地选择特征表示金字塔层级,具有更简单的网络结构、更快的检测速度。常用方法包括FCOS。
- Key-Point检测器:预测bbox一些关键点的位置,例如角点、中心或极点,并将这些关键点分组以形成框。这类方法可以使用相对小的输入图像尺寸取得相对更高的检测精度,但依赖于对单个高分辨率特征图的重复推理,因此往往需要更大的内存消耗和更长的检测时间。常用方法包括CornerNet, CenterNet。
a. Anchor-Point检测器
⚪ FCOS
FCOS预测特征图上各点的类别,再预测各点到bbox左侧、右侧、顶端和底部的距离,以及各点的center-ness score。

⚪ YOLOX
YOLOX把YOLOv3模型修改为anchor free结构,对特征图的每一个栅格位置预测$1$个目标,从而可以直接预测目标框的$4$ 个值(左上角xy坐标和box高宽);并做出如下改进:
- 解耦预测分支(分类+回归),回归分支添加IoU分支;
- 使用Mosaic和MixUp数据增强,但在最后15 epochs时关闭;
- 采用simOTA进行正负样本分配。

⚪ YOLOv6
YOLOv6 提出了一系列适用于各种工业场景的模型,包括 N/T/S/M/L,考虑到模型的大小,其架构有所不同,以获得更好的精度-速度权衡。本算法专注于检测的精度和推理效率,并在网络结构、训练策略等算法层面进行了多项改进和优化:
- 网络结构:基于 RepVGG style 设计了可重参数化、更高效的骨干网络 EfficientRep Backbone 和 Rep-PAN Neck;进一步优化设计了简洁有效的 Efficient Decoupled Head。
- 标签分配策略:前 4 个 epoch 采用 ATSS 作为标签匹配策略的 warm-up , 后续使用 TOOD 算法选择正负样本。
- 损失函数:分类损失使用的是VarifocalLoss;回归损失对于l/m/s使用的是 GIoULoss, t/n 用的是 SIoULoss。
⚪ YOLOv7
YOLOv7为实时检测器提出了高效的聚合网络和基于连接的模型缩放方法,可以更加高效地利用参数和计算量;并设计了几种可训练的bag-of-freebies,使实时检测器可以在不提高推理成本的情况下大大提高检测精度。
- 用梯度传播路径的概念分析了适用于不同网络中各层结构重参数化策略,提出了规划的模型结构重参数化,高效替代原始模块。
- 提出了一种新的标签分配方法:由粗到细的引导标签分配策略,为不同输出层分支更好的分配动态目标。
⚪ YOLOv8
- paper:Ultralytics YOLOv8
YOLOv8 是 Ultralytics 公司开源的 YOLOv5 的下一个重大更新版本,目前支持图像分类、物体检测和实例分割任务。YOLOv8 算法的核心特性和改动可以归结为如下:
- 骨干网络和 Neck 部分将 YOLOv5 的 C3 结构换成了梯度流更丰富的 C2f 结构;Head 部分换成了目前主流的解耦头结构,同时也从 Anchor-Based 换成了 Anchor-Free。
- Loss 计算方面采用了 TOOD 正样本分配策略,并引入了 Distribution Focal Loss。
- 训练的数据增强部分引入了 YOLOX 中的最后 10 epoch 关闭 Mosiac 增强的操作,可以有效地提升精度。
⚪ YOLOv9
YOLOv9是在YOLOv7的基础上进行的改进,现有方案进行逐层特征提取时会丢失大量信息,YOLOv9主要有以下2点改进:
- 设计了一种广义高效层聚合网络GELAN。GELAN将ELAN中的卷积组替换成带有RepConv的CSPNet,相当于增加网络的宽度。
- 提出可编程梯度信息PGI。PGI包括主分支、辅助可逆分支、多级辅助信息。辅助可逆分支解决网络深度带来的信息丢失问题;多级辅助信息解决深度监督带来的错误累积问题。

⚪ YOLOv10
YOLOv10模型针对YOLOv8检测流程中的后处理和模型架构进一步推进YOLOs在准确率与推理速度上的发展。
- 为了解决后处理中的冗余预测问题,YOLOv10采用一致的对偶分配策略,该策略允许模型在训练期间同时采用一对多与一对一的标签分配策略;在推理期间仅使用无需NMS的一对一预测结果。
- 通过对YOLO各个组件的全面检查,YOLOv10采用整体效率-准确性驱动的模型设计策略;为了降低计算冗余,采用轻量级分类头、空间-通道解耦下采样和秩引导的模块设计;为了提高准确率,采用大核卷积与部分自注意力模块。

b. Key-Point检测器
⚪ CornerNet
CornerNet检测目标框的左上角和右下角位置,通过Corner Pooling提取角点特征,通过预测角点嵌入进行角点匹配,并进一步预测角点位置的偏移量。

⚪ CenterNet
- paper:Objects as Points
CenterNet直接检测目标的中心点、目标的大小以及中心点的位置偏移。

⚪ RepPoints
RepPoints对特征图上面任何一点都学习出$9$个语义关键点坐标offset,同时将offset解码、refine和转换得到原始bbox。

(4) 基于Transformer的目标检测模型
⚪ DETR
DETR用Transformer架构一次性生成$N$个box预测,基于预测box和GT box的二分图匹配计算损失的大小。DETR的结构主要有三部分:
- 一个卷积神经网络backbone,用于提取紧凑的图像特征表示;
- 一个编码器-解码器结构的Transformer;
- 一个简单的前馈网络FFN,进行最终的检测预测。

⚪ Deformable DETR
Deformable DETR提出了可变形注意力模块(Deformable Attention Module),其中每个查询向量Query的查询对象通过学习一组偏移offset得到,而注意力图通过线性变换得到。

3. 目标检测的评估指标
在目标检测中,所有置信度(Confidence Score)大于阈值的检测框都被视为检测到的目标样本。根据检测框的位置以及其中目标的类别,结果可以被划分到以下几类中的一个:
- 真阳性(True Positive, TP):被正确检测的目标样本。需要满足两个条件:目标边界框与Ground Truth的交并比大于阈值;目标预测类别与标签类别匹配。
- 假阳性(False Positive, FP):被错误检测为目标样本的非目标样本。通常为边界框与Ground Truth的交并比小于阈值的样本(定位错误),或目标预测类别与标签类别不匹配的样本(分类错误)。
- 假阴性(False Negative, FN):没有被检测出的目标样本。通常为没有检测出的Ground Truth区域。
- 真阴性(True Negative, TN):检测出的非目标样本,在目标检测中通常不关心。
在划分检测框的类别时需要计算两者的交并比 (Intersection over Union, IoU),即计算检测区域与Ground Truth区域的交集与并集之比:

def IoU(pred, tar, epsilon=1e-12): # [n, 4] (x1,y1,x2,y2)
pred_area = (pred[:, 2] - pred[:, 0]) * (pred[:, 3] - pred[:, 1])
tar_area = (tar[:, 2] - tar[:, 0]) * (tar[:, 3] - tar[:, 1])
inter_lt = np.maximum(pred[:, :2], tar[:, :2])
inter_rb = np.minimum(pred[:, 2:], tar[:, 2:])
inter_wh = np.maximum(inter_rb - inter_lt, 0)
inter_area = inter_wh[:, 0] * inter_wh[:, 1]
return inter_area / (pred_area + tar_area - inter_area + epsilon)
目标检测的常用评估指标包括准确率、召回率、F-score、P-R曲线、平均准确率AP、类别平均准确率mAP。
⚪ 准确率 Precision
准确率也叫查准率,是指在所有识别出的物体中TP样本所占的比例:
\[Precision = \frac{TP}{TP+NP} = \frac{TP}{n_{pred}}\]⚪ 召回率 Recall
召回率是指在所有Ground Truth物体中TP样本所占的比例:
\[Precision = \frac{TP}{TP+FN} = \frac{TP}{n_{gt}}\]⚪ F-Score
准确率和召回率随着交并比的阈值而变化。当逐渐减小阈值时,倾向于把更多检测到的样本视为TP样本,则准确率逐渐下降,召回率逐渐增加。
F-Score是准确率和召回率的的调和平均数 (harmonic mean):
\[F_{score} = \frac{(B^2+1)PR}{B^2P+R}\]其中权重$B$调整准确率和召回率的比重关系。$B$越大则越重视召回率,$B$越小则越重视准确率。特别地,当$B=1$时称为F1-Score。
⚪ P-R曲线
对于某个指定的预测类别,可以根据给定的交并比阈值$a$把该类别下的所有预测区域划分到TP样本和FP样本。按照置信度对这些样本倒序排列后,依次计算前$i$个样本的准确率和召回率。例如:
\[\begin{array}{l|llll} \text{编号} & \text{置信度} & \text{类别}& \text{准确率}& \text{召回率} \\ \hline 1 & 88.9 & \text{TP} & 1 & 0.2 \\ 2 & 88.0 & \text{TP} & 1 & 0.4 \\ 3 & 86.5 & \text{TP} & 1 & 0.6 \\ 4 & 82.3 & \text{FP} & 0.75 & 0.6 \\ 5 & 77.2 & \text{FP} & 0.6 & 0.6 \\ 6 & 75.3 & \text{TP} & 0.667 & 0.8 \\ 7 & 67.3 & \text{FP} & 0.571 & 0.8 \\ 8 & 64.4 & \text{TP} & 0.625 & 1 \\ \end{array}\]此时召回率按照非单调递减的规律变化,而准确率大致按照递减规律变化(有时也会增加)。则可以绘制准确率-召回率曲线 (P-R plot),召回率为横轴,准确率为纵轴:

⚪ 平均准确率 Average Precision (AP)
某个类别的平均准确率 (AP)定义为该类别对应的P-R曲线之下的面积:
\[AP = \int_0^1P(r)dr\]Precision与Recall的值域在 $0$ 到 $1$ 之间,所以 AP 的值域也是在 $[0, 1]$ 范围。由于P-R曲线是由离散点构成的曲线,直接计算积分是不可行的。因此对P-R曲线进行平滑处理:给定任意一个 Recall 值,它对应的 Precision 值就等于它右侧的 Precision 中最大的值。
\[p_{interp}(r) = \mathop{\max}_{\overline{r}\geq r}P(\overline{r})\]
在Pascal VOC 2009之前计算AP值时采用差值方法:在平滑处理的P-R曲线上,取横轴 $0.2-1$ 的 $9$ 等分点的 Precision 的值,计算其平均值为最终 AP 的值。如上图中的AP值为:
\[AP = \frac{1}{9}(1\times 5 + 0.667\times 2 + 0.625\times 2) = 0.843\]上述计算方法使用的采样点较少,会有精度损失;并且在比较较小的AP值时显著性较差。在Pascal VOC 2010之后采用精度更高的方式:绘制出平滑后的P-R曲线后,用积分的方式计算平滑曲线下方的面积作为最终的 AP 值。

如上图中的AP值为:
\[AP = 1\times(0.6-0.2) + 0.667\times(0.8-0.6) + 0.625\times(1-0.8) = 0.658\]⚪ 类别平均准确率 mean Average Precision (mAP)
类别平均准确率是指计算所有类别的AP值的平均值。
4. 非极大值抑制算法
非极大值抑制 (non-maximum suppression,NMS)算法是目标检测等任务中常用的后处理方法,能够过滤掉多余的检测边界框。
NMS算法的流程如下:
- 输入边界框集合\(\mathcal{B}=\{(B_n,c_n)\}_{n=1,...,N}\),其中$c_n$是边界框$B_n$的置信度;
- 选中集合\(\mathcal{B}\)中置信度最大的边界框$B_i$,将其从集合\(\mathcal{B}\)移动至输出边界框集合\(\mathcal{O}\)中;
- 遍历集合\(\mathcal{B}\)中的其余所有边界框$B_j$,计算边界框$B_i$和边界框$B_j$的交并比$\text{IoU}(B_i,B_j)$。若$\text{IoU}(B_i,B_j)≥\text{threshold}$,则删除边界框$B_j$;
- 重复上述步骤,直至集合\(\mathcal{B}\)为空集。
# NMS from scratch
def NMS(dets, thresh):
x1, y1, x2, y2 = dets[:, 0], dets[:, 1], dets[:, 2], dets[:, 3]
scores = dets[:, 4]
areas = (x2-x1+1) * (y2-y1+1) # +1是把像素数量转换为长宽
order = scores.argsort()[::-1] # 置信度降序排列
keep = []
while order.size > 0:
i = order[0]
keep.append(i)
xx1 = np.maximum(x1[i], x1[order[1:]])
yy1 = np.maximum(y1[i], y1[order[1:]])
xx2 = np.minimum(x2[i], x2[order[1:]])
yy2 = np.minimum(y2[i], y2[order[1:]])
w = np.maximum(0., xx2 - xx1 + 1)
h = np.maximum(0., yy2 - yy1 + 1)
inter = w * h
iou = inter / (areas[i] + areas[order[1:]] - inter)
idxs = np.where(iou <= thresh)[0]
order = order[idxs + 1] # +1是修正order[1:]的偏移
return keep
# NMS via torchvision
from torchvision.ops import nms
keep = nms(
boxes, # Tensor[N, 4], (x1, y1, x2, y2) format
scores, # Tensor[N]
iou_threshold # float
) # 返回按置信度降序排列的候选框索引
boxes = boxes[keep]
NMS算法的处理精度有限、计算效率较低,主要原因包括:
- 算法采用顺序处理的模式,运算效率低;
- 根据阈值删除边界框的机制缺乏灵活性;
- 阈值通常是人工根据经验选定的;
- 评价标准是交并比IoU,只考虑两框的重叠面积。
(1)提高NMS算法的精度
提高NMS算法精度的方法包括Soft-NMS, IoU-Guided NMS, Weighted NMS, Softer-NMS, Adaptive NMS, DIoU-NMS。
⚪ Soft-NMS
对于IoU≥NMS阈值的检测框,NMS算法直接剔除这些检测框(将其置信度置零),这种严格的剔除机制对于存在遮挡的目标检测情况不友好。Soft-NMS引入得分惩罚机制,对于IoU≥阈值的检测框,使用一个与IoU正相关的惩罚函数$f(\cdot)$降低它们的置信度(而不是直接置零)。
\[s_i = \begin{cases} s_if\left( \text{IoU}(M,B_i) \right), & \text{IoU}(M,B_i) \geq \text{thresh} \\ s_i, & \text{IoU}(M,B_i) < \text{thresh} \end{cases}\]惩罚函数可以设置为线性惩罚或高斯惩罚:
\[f\left( \text{IoU}(M,B_i) \right) = 1-\text{IoU}(M,B_i) \quad \text{or} \quad e^{-\frac{\text{IoU}(M,B_i) ^2}{\sigma}}\]在对所有边界框的迭代终止之后,Soft-NMS依据预先设定的得分阈值(如$0.0001$)来保留最终的检测框。
Soft-NMS的主要缺点是处理边界框时存在定位与得分不一致的情况,即在存在遮挡目标的情况下,定位较好而得分低的框相比于定位较差而得分高的框具有更低的最终得分。
⚪ IoU-Guided NMS
考虑到边界框的定位与得分可能出现不一致的情况,IoU-Guided NMS在网络中额外引入了IoU预测分支来学习定位的置信度,进而使用定位置信度来引导NMS。

在实现时,IoU-Guided NMS使用定位置信度作为NMS的筛选依据,每次迭代挑选出具有最大定位置信度的候选框,然后将IoU≥NMS阈值的冗余框剔除,并把候选框的分类得分更新为所有冗余框及其自身的得分最大值。最终输出的框必定是同时具有最大分类得分与最大定位置信度的框。
IoU-Guided NMS有助于提高严格指标下的精度,如AP75, AP90;但需要额外添加IoU预测分支,造成计算开销。
⚪ Weighted NMS
NMS每次迭代所选出得分最大的框未必是精确定位的,而冗余框有可能是定位良好的。Weighted NMS是对边界框的坐标进行加权平均,加权平均的对象包括每次选出的候选框$M$以及IoU≥NMS阈值的冗余框。
\[M \leftarrow \frac{\sum_i w_i B_i}{\sum_i w_i}, B_i \in \{B\mid \text{IoU}(M,B)\geq \text{thresh}\} ∪ \{M\}\]其中加权权重通过对应框的得分与IoU乘积计算:\(w_i=s_i\text{IoU}(M,B_i)\)。
Weighted NMS通常能够获得更高的Precision和Recall;但其加权权重通过得分与IoU计算,前者存在得分与定位不一致问题,后者只考虑两框重叠部分,位置关系描述不够全面。
⚪ Softer-NMS
Softer-NMS也是对边界框的坐标进行加权平均,其加权平均形式为:
\[M \leftarrow \frac{\sum_i w_i B_i/\sigma_i^2}{\sum_i w_i/\sigma_i^2}, B_i \in \{B\mid \text{IoU}(M,B)\geq \text{thresh}\} ∪ \{M\}\]其中权重$w_i$计算只与IoU相关:
\[w_i = e^{-\frac{(1-\text{IoU}(M,B_i) )^2}{\sigma_t}}\]而$\sigma_i$是为每个边界框引入的定位不确定度,通过网络学习得到:

Softer-NMS可以与标准的NMS或Soft-NMS结合使用,以稳定提升检测性能。但是需要修改模型来预测方差。
⚪ Adaptive NMS
NMS算法认为与当前候选框IoU越大的框越可能是冗余框,然而当目标之间存在严重遮挡时可能存在IoU大的独立框。通常期望当目标分布稀疏时,NMS可选用小阈值以剔除更多冗余框;而当目标分布密集时,NMS选用大阈值以获得更高的召回。Adaptive NMS为网络引入了一个密度预测模块,用于学习每一个检测框的密度。

对于一个Ground Truth边界框$B_i$,其密度标签定义为:
\[d_i = \max_j \text{IoU}(B_i,B_j)\]此时预测边界框的标签修改为$(x,y,w,h,s,d)$。密度$d$越大,代表该框所处位置的目标分布越密集,越有可能是遮挡严重的地方;反之密度越小,代表该框所处位置的目标分布越稀疏,不太可能有遮挡。
Adaptive NMS将每次迭代的NMS阈值更改为:
\[thresh = \max(min\_thresh, d_M)\]Adaptive NMS可以灵活地结合到各种NMS算法中,对存在目标遮挡的检测任务更加友好;但是需要额外添加密度预测模块,造成计算开销。
⚪ DIoU-NMS
考虑到在IoU相同的情况下,一个框的中心点越靠近当前候选框$M$的中心点,则前者更有可能是冗余框。

因此使用DIoU替代IoU作为NMS的评判准则:
\[\text{DIoU} = \text{IoU} - \frac{d^2}{c^2}\]
进一步引入参数$\beta$控制中心点偏移的惩罚幅度:
\[\text{DIoU} = \text{IoU} - \left(\frac{d^2}{c^2}\right)^\beta\]当$\beta \to +\infty$时,DIoU退化为IoU;当$\beta \to 0$时,几乎所有中心点不重合的框都会被保留。
在保持NMS阈值不变的情况下,DIoU计算得到的结果会小一些,因此会保留更多的框,从而实现更大的召回率,有助于缓解遮挡案例;然而每次迭代剩余更多的框会增加迭代轮数,进一步降低运算效率。
(2)提高NMS算法的效率
NMS中的IoU计算是顺序处理的。假设图像中一共有$N$个检测框,每一个框都需要和其余所有框计算一次IoU,则计算复杂度是$O(\frac{N(N-1)}{2})=O(N^2)$。
提高NMS算法效率的方法包括CUDA NMS, Fast NMS, Cluster NMS, Matrix NMS。
⚪ CUDA NMS
CUDA NMS是NMS的GPU版本,旨在将IoU的计算并行化,并通过矩阵运算加速。
若将边界框集合\(\mathcal{B}\)按照置信度得分从高到低排序,即$B_1$是得分最高的框,$B_N$是得分最低的框;则可以计算IoU矩阵:
\[X=\text{IoU}(B,B)= \begin{pmatrix} x_{11} & x_{12} & ... & x_{1N} \\ x_{21} & x_{22} & ... & x_{2N} \\ ... & ... & ... & ... \\ x_{N1} & x_{N2} & ... & x_{NN} \\ \end{pmatrix} , \quad x_{ij}=\text{IoU}(B_i,B_j)\]通过GPU的并行加速能力,可以一次性得到IoU矩阵的全部计算结果。
许多深度学习框架已将CUDA NMS作为基本函数使用,如Pytorch在torchvision 0.3版本中正式集成了CUDA NMS。下面是CUDA NMS计算IoU矩阵的一种简单实现。
def box_iou(boxes1, boxes2): # input: [M, 4], [N, 4]
def box_area(box): # (x1, y1, x2, y2)
return (box[2] - box[0]) * (box[3] - box[1])
area1 = box_area(boxes1.t()) # [M,]
area2 = box_area(boxes2.t()) # [N,]
lt = torch.max(boxes1[:, None, :2], boxes2[:, :2]) # [M,N,2]
rb = torch.min(boxes1[:, None, 2:], boxes2[:, 2:]) # [M,N,2]
inter = (rb - lt).clamp(min=0).prod(2) # [M, N]
return inter / (area1[:, None] + area2 - inter) # [M, N]
计算得到IoU矩阵后,需要利用它抑制冗余框。可以采用矩阵查询的方法(仍然需要顺序处理,但计算IoU本身已经被并行加速);也可以使用下面提出的一些算法。
⚪ Fast NMS
根据IoU矩阵的计算规则可以得出$\text{IoU}(B_i,B_j)=\text{IoU}(B_j,B_i)$,且计算$\text{IoU}(B_i,B_i)$是没有意义的。因此IoU矩阵$X$是对称矩阵。
Fast NMS算法首先对矩阵$X$使用pytorch提供的triu函数进行上三角化,得到上三角矩阵:
若按照NMS的规则,应该按行依次遍历矩阵$X$,如果某行$i$中元素$x_{ij}=\text{IoU}(B_i,B_j),j>i$超过阈值,则应剔除边界框$B_j$,且不再考虑$j$所对应的行与列。
Fast NMS则对上述规则进行了化简,其思路是只要边界框$B_j$与任意边界框$B_i$重合度较大(超过阈值),则认为其是冗余框,将其剔除。对矩阵$X$执行按列取最大值的操作,得到一维向量$b=[b_1,b_2,…,b_N]$,$b_n$代表矩阵$X$的第$n$列中元素的最大值(即边界框$B_j$与其余边界框的最大IoU)。然后进行阈值二值化:$b$中元素小于阈值对应保留的边界框,$b$中元素大于阈值对应冗余框。
Fast NMS容易删除更多边界框,因为假如边界框$B_j$与边界框$B_i$重合度较大,但边界框$B_i$已经被剔除,则边界框$B_j$还是有可能会被保留的。一个简单的例子如下,注意到边界框$B_4$被错误地剔除了。
\[\begin{aligned} X&= \begin{pmatrix} 0 & 0.6 & 0.1 & 0.3 & 0.8 \\ & 0 & 0.2 & 0.72 & 0.1 \\ & & 0 & 0.45 & 0.12 \\ & & & 0 & 0.28 \\ & & & & 0 \\ \end{pmatrix} \\ & \downarrow (\text{按列取最大值}) \\ b &= [0, 0.6,0.2,0.72,0.8] \\ & \downarrow (\text{选定阈值为0.5}) \\ b &= [1,0,1,0,0] \\ &(\text{保留边界框1和边界框3}) \end{aligned}\]使用pytorch实现Fast NMS算法如下:
def fast_nms(boxes, scores, NMS_threshold:float=0.5):
scores, idx = scores.sort(0, descending=True)
boxes = boxes[idx] # 对框按得分降序排列
iou = box_iou(boxes, boxes) # IoU矩阵
iou.triu_(diagonal=1) # 上三角化
keep = iou.max(dim=0)[0] < NMS_threshold # 列最大值向量,二值化
return boxes[keep], scores[keep]
Fast NMS算法比NMS算法运算速度更快,但由于其会抑制更多边界框,会导致性能略微下降。
⚪ Cluster NMS
Cluster NMS算法旨在弥补Fast NMS算法性能下降的问题,同时保持较快的运算速度。
定义边界框的cluster,若边界框$B_i$属于该cluster,则边界框$B_i$与集合内任意边界框$B_j$的交并比$\text{IoU}(B_i,B_j)$均超过阈值,且边界框$B_i$与不属于该集合的任意边界框$B_k$的交并比$\text{IoU}(B_i,B_k)$均低于阈值。通过定义cluster将边界框分成不同的簇,如下图可以把边界框分成三组cluster:

Cluster NMS算法本质上是Fast NMS算法的迭代式。算法前半部分与Fast NMS算法相同,都是按降序排列边界框、计算IoU矩阵、矩阵上三角化、按列取最大值、阈值二值化得到一维向量$b$。
不同于Fast NMS算法直接根据向量$b$输出结果,Cluster NMS算法将向量$b$按列复制后将其右乘到IoU矩阵中。然后再对新的矩阵按列取最大值、阈值二值化,得到新的向量$b$,再将其扩展后右乘IoU矩阵,直至相邻迭代中向量$b$不再变化。

矩阵右乘相当于进行行变换。向量$b$扩展后右乘到IoU矩阵,若$b$的第$n$项为$0$,代表对应的边界框$B_n$是冗余框,则不应考虑该框对其他框产生的影响,因此将IoU矩阵的第$n$行置零;反之若$b$的第$n$项为$1$,代表对应的边界框$B_n$不是冗余框,因此保留IoU矩阵的第$n$行。由数学归纳法可证,Cluster NMS算法的收敛结果与NMS算法相同。
使用pytorch实现Cluster NMS算法如下:
def cluster_nms(boxes, scores, NMS_threshold:float=0.5, epochs:int=200):
scores, idx = scores.sort(0, descending=True)
boxes = boxes[idx].view_as(boxes) # 对框按得分降序排列
iou = box_iou(boxes, boxes).triu_(diagonal=1) # IoU矩阵,上三角化
C = iou
for i in range(epochs):
A = C
maxA = A.max(dim=0)[0] # 列最大值向量
E = (maxA < NMS_threshold).float() # 二值化
E = E.unsqueeze(1).expand_as(A) # 对角矩阵E的替代
C = iou.mul(E) # 按元素相乘
if A.equal(C)==True: # 终止条件
break
keep = maxA < NMS_threshold
return boxes[keep], scores[keep]
NMS算法顺序处理每一个边界框,会在所有cluster上迭代,在计算时重复计算了不同cluster之间的边界框。Cluster NMS算法通过行变换使得迭代进行在拥有框数量最多的cluster上,其迭代次数不超过图像中最大cluster所拥有的边界框个数。因此Cluster NMS算法适合图像中有很多cluster的场合。
实践中又提出了一些Cluster NMS的变体:
⭐ Cluster NMS + Soft-NMS:引入得分惩罚机制
得分惩罚机制(score penalty mechanism, SPM)是指每次迭代后根据计算得到的IoU矩阵对边界框的置信度得分进行惩罚,即与该边界框重合度高的框越多,该边界框的置信度越低:
\[s_j = s_j \cdot \prod_{i}^{} e^{-\frac{c_{ij}^2}{\sigma}}\]def SPM_cluster_nms(boxes, scores, NMS_threshold:float=0.5, epochs:int=200):
scores, idx = scores.sort(0, descending=True)
boxes = boxes[idx].view_as(boxes) # 对框按得分降序排列
iou = box_iou(boxes, boxes).triu_(diagonal=1) # IoU矩阵,上三角化
C = iou
for i in range(epochs):
A = C
maxA = A.max(dim=0)[0] # 列最大值向量
E = (maxA < NMS_threshold).float() # 二值化
E = E.unsqueeze(1).expand_as(A) # 对角矩阵E的替代
C = iou.mul(E) # 按元素相乘
if A.equal(C)==True: # 终止条件
break
scores = torch.prod(torch.exp(-C**2/0.2),0)*scores #惩罚得分
keep = scores > 0.1 #得分阈值筛选
return boxes[keep], scores[keep]
⭐ Cluster NMS + DIoU-NMS:引入中心点距离修正
将IoU替换成DIoU,即在IoU的基础上加上中心点的归一化距离,能够更好的表达两框的距离;并对得分惩罚机制进行修改:
\[s_j = s_j \cdot \prod_{i}^{} \mathop{\min} \{ e^{-\frac{c_{ij}^2}{\sigma}} + (1-\text{DIoU})^{\beta}, 1 \}\]上式中$\beta$用于控制中心点距离惩罚的程度,$\min$避免惩罚因子超过$1$。
⭐ Cluster NMS + Weighted NMS:引入加权平均法
在计算IoU矩阵时考虑边界框置信度得分的影响,即每次迭代时将IoU矩阵与边界框的置信度得分向量按列相乘。
def Weighted_cluster_nms(boxes, scores, NMS_threshold:float=0.5, epochs:int=200):
scores, idx = scores.sort(0, descending=True)
boxes = boxes[idx].view_as(boxes) # 对框按得分降序排列
iou = box_iou(boxes, boxes).triu_(diagonal=1) # IoU矩阵,上三角化
C = iou
for i in range(epochs):
A = C
maxA = A.max(dim=0)[0] # 列最大值向量
E = (maxA < NMS_threshold).float() # 二值化
E = E.unsqueeze(1).expand_as(A) # 对角矩阵E的替代
C = iou.mul(E) # 按元素相乘
if A.equal(C)==True: # 终止条件
break
keep = maxA < NMS_threshold # 列最大值向量,二值化
weights = C*(C>NMS_threshold).float() + torch.eye(C.shape[0])
weights = weights * scores.reshape((1,-1))
xx1 = boxes[:,0].unsqueeze(1)
yy1 = boxes[:,1].unsqueeze(1)
xx2 = boxes[:,2].unsqueeze(1)
yy2 = boxes[:,3].unsqueeze(1)
weightsum = weights.sum(dim=1) # 坐标加权平均
xx1 = (xx1*weights).sum(dim=1)/(weightsum)
yy1 = (yy1*weights).sum(dim=1)/(weightsum)
xx2 = (xx2*weights).sum(dim=1)/(weightsum)
yy2 = (yy2*weights).sum(dim=1)/(weightsum)
boxes = torch.stack([xx1, yy1, xx2, yy2], 1)
return boxes[keep], scores[keep]
⚪ Matrix NMS
Matrix NMS算法是对Soft-NMS算法的并行实现。在Soft-NMS算法中,对于每个边界框$B_j$,如果存在与其IoU超过阈值的边界框$B_i$,则说明$B_j$可能是潜在的冗余框,对其置信度得分$s_j$施加一定的惩罚:
\[s_j \leftarrow s_j f\left(\text{IoU}(B_i,B_j)\right)\]Soft-NMS算法在计算惩罚系数时是串行实现的。为了并行地计算惩罚系数,Matrix NMS考虑以下两点:
- 计算每个满足$s_i>s_j$的边界框$B_i$对边界框$B_j$的惩罚;
- 计算边界框$B_i$被其余边界框抑制的概率。
Matrix NMS对边界框$B_j$的惩罚系数计算为:
\[w_j = \mathop{\min}_{\forall s_i > s_j} \frac{f\left(\text{IoU}(B_i,B_j)\right)}{\mathop{\min}_{\forall s_k > s_i}f\left(\text{IoU}(B_i,B_k)\right)}\]其中惩罚函数的设置与Soft-NMS相同,可以设置为线性惩罚或高斯惩罚:
\[f\left( \text{IoU}(M,B_i) \right) = 1-\text{IoU}(M,B_i) \quad \text{or} \quad e^{-\frac{\text{IoU}(M,B_i) ^2}{\sigma}}\]def matrix_nms(boxes, scores, method='gauss', sigma=0.5):
iou = box_iou(boxes, boxes).triu_(diagonal=1) # IoU矩阵,上三角化
iou_cmax = iou.max(dim=0)[0] # 计算Bj的最大IoU
iou_cmax = iou_cmax.expand(iou.shape[0], iou.shape[0]).T
if method == 'gauss':
decay = torch.exp(-(iou**2-iou_cmax**2)/sigma)
else:
decay = (1 - iou) / (1 - iou_cmax)
decay = decay.min(dim=0)[0]
return scores * decay
5. 目标检测中的损失函数
目标检测中的损失函数包括边界框的分类损失和回归损失。其中分类损失用于区分边界框的类别,即边界框内目标的类别,对于两阶段的检测方法还包含边界框的正负类别;常用的分类损失函数包括Cross-Entropy loss, Focal loss, Generalized Focal Loss, Varifocal Loss, GHM, Poly loss。
而回归损失衡量预测边界框坐标$x_{pred}$和GT边界框坐标$x_{gt}$之间的差异,常用的回归损失函数包括L1 / L2 loss, Smooth L1 loss, Dynamic SmoothL1 Loss, Balanced L1 loss, IoU loss, GIoU loss, DIoU loss, CIoU loss, EIoU loss, SIoU loss, MPDIoU loss。
(1)常用的分类损失
⚪ Cross-Entropy loss
通用的分类损失采用交叉熵损失(Cross-Entropy loss)。给定网络输出边界框的预测类别概率分布$p=(p_0,…,p_K)$和标签类别$c$ ($0$表示背景类),则可以构造多元交叉熵损失:
\[\begin{aligned} \mathcal{L}_{cls}(p,c) &= -\log p_c \\ \end{aligned}\]对于一些两阶段的目标检测算法(如Faster RCNN),需要对RPN提取的proposal边界框进行二分类(区分是否为包含目标的边界框),此时需要构造二元交叉熵损失:
\[\begin{aligned} \mathcal{L}_{cls}(\hat{p},p) &= -p \log \hat{p} - (1-p) \log (1-\hat{p}) \\ \end{aligned}\]⚪ Focal Loss
目标检测中的边界框分类问题是一种类别不平衡分类,即大部分边界框都是无目标的背景框。
Focal loss显式地引入了权重因子$(1-p_t)^{\gamma},\gamma \geq 0$,使得$p_t$(目标类别的预测置信度)越大时权重越小,即对容易分类的样本减少权重。此外为了更好地控制损失函数的形状,额外引入一个权重系数$\alpha$。
\[\mathcal{L}_{\text{focal}}(p,t) = -\alpha(1-p_t)^\gamma \log p_t\]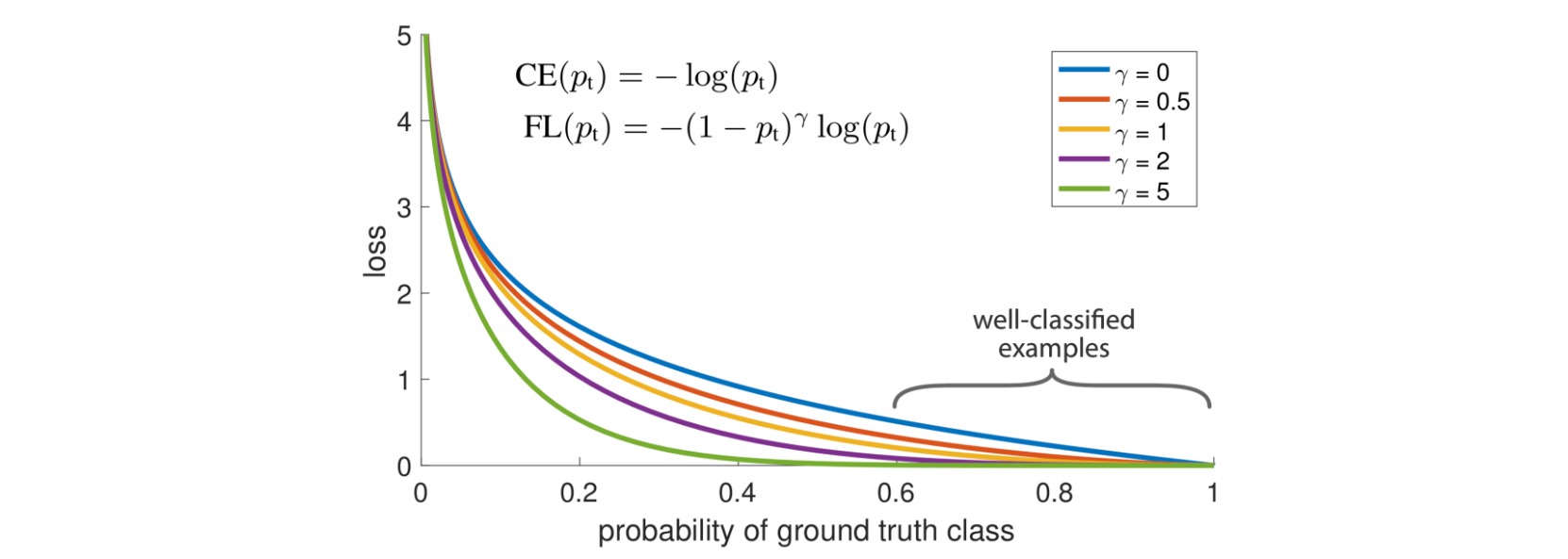
⚪ Generalized Focal Loss (GFL)

Quality Focal Loss (QFL) 将离散标签的 Focal Loss 泛化到连续标签上,将预测框与 GT 的 IoU 软化作为分类分数的标签,使得分类分数关联回归质量。
\[QFL(p) = -|y-p|^\beta \left( y\log p + (1-y) \log(1-p) \right)\]Distribution Focal Loss (DFL) 把边界框位置建模为离散分布$S$,以类似交叉熵的形式去优化浮点值标签$y$的左右整数值$y_i$和$y_{i+1}$两个位置的概率。
\[DFL(S_i, S_{i+1}) = -\left( (y_{i+1}-y)\log S_i + (y-y_i) \log S_{i+1} \right)\]QFL和DFL可以统一地表示为GFL:
\[GFL\left(p_{y_l}, p_{y_r}\right)=-\left|y-\left(y_l p_{y_l}+y_r p_{y_r}\right)\right|^\beta\left(\left(y_r-y\right) \log \left(p_{y_l}\right)+\left(y-y_l\right) \log \left(p_{y_r}\right)\right)\]GFLV2则进一步用DFL分布形状的统计量去指导最终定位质量的估计。直接取学习到分布的Topk数值concat在一起形成一个维度非常低的输入特征向量,用这个向量再接一个非常小的全连接层,最后再变成一个Sigmoid之后的scalar乘到原来的分类表征中。
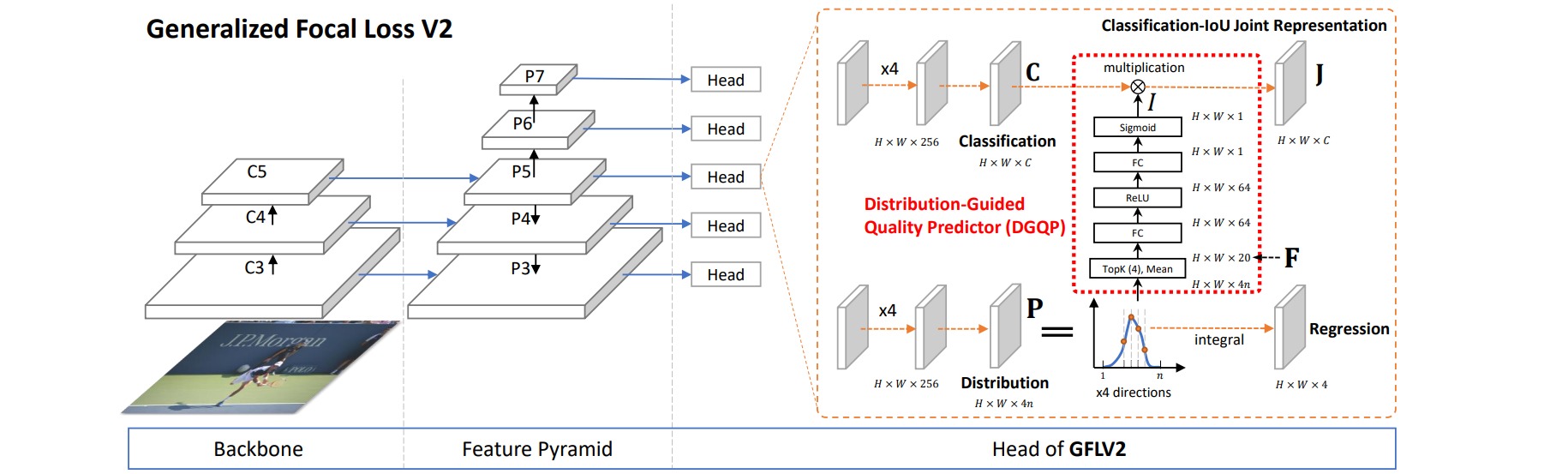
⚪ Varifocal Loss
Varifocal Loss针对正负样本提出了非对称的加权操作:
\[VFL(p) = \begin{cases} -y \left( y\log p + (1-y) \log(1-p) \right) & y > 0 \\ -\alpha p^\gamma \log(1-p) & y = 0 \end{cases}\]其中 $y$ 是预测 bboxes 与 GT 的 IoU,使用软标签的形式作为分类的标签。 $p\in[0,1]$ 表示分类分数。
- 对于负样本,即当 $y = 0$ 时,使用 $\alpha p^\gamma$ 作为 focal weight 使样本聚焦于困难样本上,这与 Focal Loss 基本一致。
- 对于正样本,即当 $y > 0$ 时,首先计算标准二值交叉熵部分,正样本的权重设置使用分类的标签 $y$, 即 IoU 作为 focal weight, 使得聚焦到具有高质量的样本上。
⚪ Gradient Harmonized Mechanism (GHM)
对于一个已经收敛的目标检测模型,依然有部分样本梯度范数接近$1$,这些样本极可能是外点数据即标注有错误的数据,如果训练时候强行拟合,对最终性能反而有影响。
GHM对loss两端的梯度进行降低权重,具备了易学习样本降低损失权重并且外点数据梯度不会过大的效果。在实现时计算梯度密度函数,并把密度分布的倒数设置为样本的权值。
\[\begin{gathered} \hat{L}_{G H M-C}=\frac{1}{N} \sum_{i=1}^N \hat{\beta}_i L_{C E}\left(p_i, p_i^*\right) \\ =\sum_{i=1}^N \frac{L_{C E}\left(p_i, p_i^*\right)}{G D\left(g_i\right)} \\ \end{gathered}\]⚪ Poly Loss
交叉熵损失可以被泰勒展开为一系列多项式函数的线性组合:
\[\begin{aligned} \mathcal{L}_{CE}(p,t) &= -\log p_t = \sum_{j=1}^\infty \frac{1}{j} (1-p_t)^j \\ &= (1-p_t)+ \frac{1}{2} (1-p_t)^2 +\frac{1}{3} (1-p_t)^3 + \cdots \\ \end{aligned}\]其中低阶部分倾向于得到正确的预测结果,高阶部分倾向于防止预测结果出错(如缓解类别不平衡问题)。Poly Loss为前$N$个多项式项引入扰动$\epsilon_1,…,\epsilon_N$,用于对更精确的任务目标进行更精确的调整。
\[\begin{aligned} \mathcal{L}_{\text{Poly-N}}(p,t) &= (\epsilon_1+1)(1-p_t)+ \cdots +\left(\epsilon_N+\frac{1}{N}\right) (1-p_t)^N + \sum_{j=N+1}^\infty \frac{1}{j} (1-p_t)^j \\ &= -\log p_t + \sum_{j=1}^N \epsilon_j (1-p_t)^j \end{aligned}\](2)常用的回归损失
⚪ L1 / L2 Loss
通用的回归损失采用L1 / L2 loss,计算如下:
\[L1 = |x| \qquad L2 = x^2\]这两种损失函数存在缺点:
- L1 Loss的导数为常数,在训练后期,真实值与预测值的差值$x=x_{gt}-x_{pred}$很小时,如果学习率不变,损失函数会在稳定值附近波动,难以收敛到更高精度;
- L2 Loss在差值很大时,其导数非常大,故在训练初期不稳定。
⚪ smooth L1 loss
- paper:Fast R-CNN
针对L1 / L2 loss存在的问题,修正后得到smooth L1 loss:
\[\text{smooth-L1}(x) = \begin{cases} |x|-0.5, & |x| ≥ 1 \\ 0.5x^2, &|x| < 1 \end{cases}\]该损失函数在差值$x$较大时是L1 Loss,在其较小时是L2 Loss。也可以引入一个方差系数:
\[\text{smooth-L1}(x, \sigma) = \begin{cases} |x|-0.5/\sigma^2, & |x| ≥ 1/\sigma^2 \\ 0.5\sigma^2x^2, &|x| < 1/\sigma^2 \end{cases}\]def smoothL1Loss(pred_loc, gt_loc, sigma):
sigma_squared = sigma ** 2
regression_diff = (gt_loc - pred_loc)
regression_diff = regression_diff.abs().float()
regression_loss = torch.where(
regression_diff < (1. / sigma_squared),
0.5 * sigma_squared * regression_diff ** 2,
regression_diff - 0.5 / sigma_squared
)
return regression_loss.mean()
⚪ Dynamic SmoothL1 Loss
\[\text{DSL}(x, \beta_{now}) = \begin{cases} |x|-0.5\beta_{now}, & |x| ≥ \beta_{now} \\ 0.5x^2/\beta_{now}, &|x| < \beta_{now} \end{cases}\]$\beta_{now}$是需要动态确定的。其确定规则是先计算预测值和GT的回归误差,然后选择第$K_{\beta-th}$个最小值,然后在达到迭代次数后,采用中位数作为设置值。
随着训练进行,高质量样本越来越多,回归误差会越来越小,并且高质量的预测框其误差会更小。引入动态$\beta_{now}$减少来修正,来增加高质量部分样本的梯度,可以不断突出高质量预测框的回归误差。
⚪ balances L1 loss
Balanced L1 Loss首先设计梯度的函数,增加梯度绝对值小于$1$的样本(inlier)的梯度值,以帮助网络更好地定位,也使得分类和回归过程更加均衡。梯度形式为:
\[\frac{\partial L_b}{\partial x} = \begin{cases} \alpha \ln (b|x|+1), & |x| < 1 \\ \gamma, & |x| ≥ 1 \end{cases}\]在梯度表达式的基础上,积分得到Balanced L1 Loss的表达式:
\[L_b(x)= \begin{cases}\frac{\alpha}{b}(b|x|+1) \ln (b|x|+1)-\alpha|x| & \text { if }|x|<1 \\ \gamma|x|+C & \text { otherwise }\end{cases}\]上述介绍的损失函数存在共通的缺点:
- 这些损失函数独立地计算每一个坐标分量(如$x$,$y$,$h$,$w$)的差异,然后相加得到最终的损失。这样做忽略了不同坐标分量之间的联系(如$x$,$y$靠近图像边缘时,$h$,$w$会受到限制);
- 目标检测中,评估边界框定位质量的指标是交并比 IoU,与上述损失函数的计算是不匹配的(具有相同损失值的不同坐标组合可能具有不同的IoU)。
⚪ IoU loss
为使得边界框的定位与其评估指标IoU相匹配,不妨直接把IoU设置为损失函数(IoU loss):
\[\text{IoU loss} = -\log\frac{\text{intersection}(x_{gt},x_{pred})}{\text{union}(x_{gt},x_{pred})}\]实际计算中也简化为:
\[\text{IoU loss} = 1-\frac{\text{intersection}(x_{gt},x_{pred})}{\text{union}(x_{gt},x_{pred})}\]该损失将边界框的不同坐标分量(如$x$,$y$,$h$,$w$)联系起来,具有尺度不变性。
def IoULoss(b1, b2): # [n, 4] format: xywh
# 求出预测框左上角右下角
b1_xy = b1[..., :2]
b1_wh = b1[..., 2:4]
b1_wh_half = b1_wh/2.
b1_mins = b1_xy - b1_wh_half
b1_maxes = b1_xy + b1_wh_half
# 求出真实框左上角右下角
b2_xy = b2[..., :2]
b2_wh = b2[..., 2:4]
b2_wh_half = b2_wh/2.
b2_mins = b2_xy - b2_wh_half
b2_maxes = b2_xy + b2_wh_half
# 求真实框和预测框所有的iou
intersect_mins = torch.max(b1_mins, b2_mins)
intersect_maxes = torch.min(b1_maxes, b2_maxes)
intersect_wh = torch.max(intersect_maxes - intersect_mins, torch.zeros_like(intersect_maxes))
intersect_area = intersect_wh[..., 0] * intersect_wh[..., 1]
b1_area = b1_wh[..., 0] * b1_wh[..., 1]
b2_area = b2_wh[..., 0] * b2_wh[..., 1]
union_area = b1_area + b2_area - intersect_area
iou = intersect_area / union_area
return 1-iou
IoU loss的缺点:
- 当预测边界框和实际边界框不相交时,IoU为$0$。此时IoU loss是不可导的,不能反映两个边界框的远近程度,无法优化;
- 假设预测框和目标框的大小都确定,只要两个框的相交值是确定的,其IoU值是相同时,不能反映两个框是如何相交的。如下图所示,通常认为右边的边界框更好,但两者IoU值相同:

⚪ GIoU loss
IoU不能区分一些边界框的相交情况。作者提出了评估指标GIoU (Generalized IoU),不仅关注重叠区域,还关注非重叠区域,能更好的反映两者的重合度。计算如下:
\[\text{GIoU} = \text{IoU} - \frac{|C-(A∪B)|}{|C|}\]其中$A$、$B$表示两个边界框区域,$C$表示$A$和$B$的外接矩形。GIoU的取值范围是$-1 \sim 1$,当两框重合时取$1$,当两框未相交时取$-1$。
通过GIoU可以定义GIoU loss:
\[\text{GIoU loss} = 1-\text{GIoU}\]def GIoULoss(b1, b2): # [n, 4] format: xywh
# 求出预测框左上角右下角
b1_xy = b1[..., :2]
b1_wh = b1[..., 2:4]
b1_wh_half = b1_wh/2.
b1_mins = b1_xy - b1_wh_half
b1_maxes = b1_xy + b1_wh_half
# 求出真实框左上角右下角
b2_xy = b2[..., :2]
b2_wh = b2[..., 2:4]
b2_wh_half = b2_wh/2.
b2_mins = b2_xy - b2_wh_half
b2_maxes = b2_xy + b2_wh_half
# 求真实框和预测框所有的iou
intersect_mins = torch.max(b1_mins, b2_mins)
intersect_maxes = torch.min(b1_maxes, b2_maxes)
intersect_wh = torch.max(intersect_maxes - intersect_mins, torch.zeros_like(intersect_maxes))
intersect_area = intersect_wh[..., 0] * intersect_wh[..., 1]
b1_area = b1_wh[..., 0] * b1_wh[..., 1]
b2_area = b2_wh[..., 0] * b2_wh[..., 1]
union_area = b1_area + b2_area - intersect_area
iou = intersect_area / union_area
# 找到真实框和预测框的外接矩形
enclose_mins = torch.min(b1_mins, b2_mins)
enclose_maxes = torch.max(b1_maxes, b2_maxes)
enclose_wh = torch.max(enclose_maxes - enclose_mins, torch.zeros_like(intersect_maxes))
# 计算GIoU
enclose_area = enclose_wh[..., 0] * enclose_wh[..., 1]
giou = iou - (enclose_area - union_area) / enclose_area
return 1-giou
GIoU loss的缺点:
- 当一个边界框完全包含另一个边界框时,GIoU退化为IoU,无法区分两者的相对位置关系。如下图三者的GIoU相同,但我们认为右边的结果更好:

⚪ DIoU loss
作者分析边界框回归的三个重要因素:中心点距离、重叠面积和长宽比。笔者的理解如下,对于给定的GT边界框,中心点距离能够对预测框进行粗定位,重叠面积能够进一步筛选预测框,长宽比能够最终确定预测框。
IoU只衡量重叠面积,需要进一步考虑预测框和GT框的惩罚项,损失函数的通用范式如下:
\[L = 1-IoU+R(B_{pred},B_{gt})\]作者提出了评估指标DIoU (Distance IoU),将惩罚项设置为:
\[R_{DIoU} = \frac{ρ^2(b_{pred},b_{gt})}{c^2}\]其中$b_{pred}$,$b_{gt}$表示边界框的中心点,$ρ$是欧式距离,$c$表示最小外接矩形的对角线距离,如下图所示:

DIoU是在IoU的基础上加上中心点的归一化距离惩罚,能够更好的表达两框之间的距离,计算如下:
\[\text{DIoU} = \text{IoU} - R_{DIoU}\]通过DIoU可以定义DIoU loss:
\[\text{DIoU loss} = 1-\text{DIoU}\]def DIoULoss(b1, b2): # [n, 4] format: xywh
# 求出预测框左上角右下角
b1_xy = b1[..., :2]
b1_wh = b1[..., 2:4]
b1_wh_half = b1_wh/2.
b1_mins = b1_xy - b1_wh_half
b1_maxes = b1_xy + b1_wh_half
# 求出真实框左上角右下角
b2_xy = b2[..., :2]
b2_wh = b2[..., 2:4]
b2_wh_half = b2_wh/2.
b2_mins = b2_xy - b2_wh_half
b2_maxes = b2_xy + b2_wh_half
# 求真实框和预测框所有的iou
intersect_mins = torch.max(b1_mins, b2_mins)
intersect_maxes = torch.min(b1_maxes, b2_maxes)
intersect_wh = torch.max(intersect_maxes - intersect_mins, torch.zeros_like(intersect_maxes))
intersect_area = intersect_wh[..., 0] * intersect_wh[..., 1]
b1_area = b1_wh[..., 0] * b1_wh[..., 1]
b2_area = b2_wh[..., 0] * b2_wh[..., 1]
union_area = b1_area + b2_area - intersect_area
iou = intersect_area / union_area
# 找到真实框和预测框的外接矩形
enclose_mins = torch.min(b1_mins, b2_mins)
enclose_maxes = torch.max(b1_maxes, b2_maxes)
enclose_wh = torch.max(enclose_maxes - enclose_mins, torch.zeros_like(intersect_maxes))
# 计算中心的距离
center_wh = b1_xy - b2_xy
center_distance = torch.sum(torch.pow(center_wh, 2), axis=-1)
# 计算对角线距离
enclose_diagonal = torch.sum(torch.pow(enclose_wh, 2), axis=-1)
# 计算DIoU
diou = iou - 1.0 * (center_distance) / torch.clamp(enclose_diagonal, min = 1e-6)
return 1-diou
DIoU loss的缺点是没有考虑边界框的长宽比的影响。
⚪ CIoU loss
DIoU的作者又进一步提出了CIoU (Complete IoU),在惩罚项上增加长宽比影响因子$\alpha v$:
\[R_{CIoU} = \frac{ρ^2(b_{pred},b_{gt})}{c^2} + \alpha v\]其中$v$衡量边界框长宽比的一致性,$\alpha$用于平衡$v$的值,计算如下:
\[\begin{aligned} v &= \frac{4}{\pi^2} (\arctan\frac{w^{gt}}{h^{gt}}-\arctan\frac{w}{h})^2 \\ \alpha &= \frac{v}{(1-\text{IoU})+v} \end{aligned}\]通过CIoU可以定义CIoU loss:
\[\text{CIoU loss} = 1-\text{CIoU}\]def CIoULoss(b1, b2): # [n, 4] format: xywh
# 求出预测框左上角右下角
b1_xy = b1[..., :2]
b1_wh = b1[..., 2:4]
b1_wh_half = b1_wh/2.
b1_mins = b1_xy - b1_wh_half
b1_maxes = b1_xy + b1_wh_half
# 求出真实框左上角右下角
b2_xy = b2[..., :2]
b2_wh = b2[..., 2:4]
b2_wh_half = b2_wh/2.
b2_mins = b2_xy - b2_wh_half
b2_maxes = b2_xy + b2_wh_half
# 求真实框和预测框所有的iou
intersect_mins = torch.max(b1_mins, b2_mins)
intersect_maxes = torch.min(b1_maxes, b2_maxes)
intersect_wh = torch.max(intersect_maxes - intersect_mins, torch.zeros_like(intersect_maxes))
intersect_area = intersect_wh[..., 0] * intersect_wh[..., 1]
b1_area = b1_wh[..., 0] * b1_wh[..., 1]
b2_area = b2_wh[..., 0] * b2_wh[..., 1]
union_area = b1_area + b2_area - intersect_area
iou = intersect_area / union_area
# 找到真实框和预测框的外接矩形
enclose_mins = torch.min(b1_mins, b2_mins)
enclose_maxes = torch.max(b1_maxes, b2_maxes)
enclose_wh = torch.max(enclose_maxes - enclose_mins, torch.zeros_like(intersect_maxes))
# 计算中心的距离
center_wh = b1_xy - b2_xy
center_distance = torch.sum(torch.pow(center_wh, 2), axis=-1)
# 计算对角线距离
enclose_diagonal = torch.sum(torch.pow(enclose_wh, 2), axis=-1)
diou = iou - 1.0 * (center_distance) / torch.clamp(enclose_diagonal, min = 1e-6)
v = (4 / (math.pi ** 2)) * torch.pow((torch.atan(b1_wh[..., 0] / torch.clamp(b1_wh[..., 1],min = 1e-6)) - torch.atan(b2_wh[..., 0] / torch.clamp(b2_wh[..., 1], min = 1e-6))), 2)
alpha = v / torch.clamp((1.0 - iou + v), min = 1e-6)
ciou = diou - alpha * v
return 1-ciou
CIoU loss的主要缺点如下:
- 衡量长宽比的$v$计算过于复杂,减缓了收敛速度;
- 推导可得$\frac{\partial v}{\partial w}=-\frac{h}{w}\frac{\partial v}{\partial h}$,$w$和$h$的优化是相反的。
⚪ EIoU loss
为简化CIoU中长宽比影响因子$\alpha v$的计算,作者提出EIoU (Efficient IoU),用下式代替长宽比的影响因子$\alpha v$:
\[\frac{ρ^2(w_{pred},w_{gt})}{c_w^2} + \frac{ρ^2(h_{pred},h_{gt})}{c_h^2}\]EIoU的定义如下:
\[\text{EIoU} = \text{IoU} - \frac{ρ^2(b_{pred},b_{gt})}{c^2}-\frac{ρ^2(w_{pred},w_{gt})}{c_w^2} - \frac{ρ^2(h_{pred},h_{gt})}{c_h^2}\]通过EIoU可以定义EIoU loss:
\[\text{EIoU loss} = 1-\text{EIoU}\]def EIoULoss(b1, b2): # [n, 4] format: xywh
# 求出预测框左上角右下角
b1_xy = b1[..., :2]
b1_wh = b1[..., 2:4]
b1_wh_half = b1_wh/2.
b1_mins = b1_xy - b1_wh_half
b1_maxes = b1_xy + b1_wh_half
# 求出真实框左上角右下角
b2_xy = b2[..., :2]
b2_wh = b2[..., 2:4]
b2_wh_half = b2_wh/2.
b2_mins = b2_xy - b2_wh_half
b2_maxes = b2_xy + b2_wh_half
# 求真实框和预测框所有的iou
intersect_mins = torch.max(b1_mins, b2_mins)
intersect_maxes = torch.min(b1_maxes, b2_maxes)
intersect_wh = torch.max(intersect_maxes - intersect_mins, torch.zeros_like(intersect_maxes))
intersect_area = intersect_wh[..., 0] * intersect_wh[..., 1]
b1_area = b1_wh[..., 0] * b1_wh[..., 1]
b2_area = b2_wh[..., 0] * b2_wh[..., 1]
union_area = b1_area + b2_area - intersect_area
iou = intersect_area / union_area
# 找到真实框和预测框的外接矩形
enclose_mins = torch.min(b1_mins, b2_mins)
enclose_maxes = torch.max(b1_maxes, b2_maxes)
enclose_wh = torch.max(enclose_maxes - enclose_mins, torch.zeros_like(intersect_maxes))
# 计算EIoU
enclose_squared_w = enclose_wh[..., 0] ** 2
enclose_squared_h = enclose_wh[..., 1] ** 2
enclose_squared_diag = enclose_squared_w + enclose_squared_h
center_squared_w = (b1_xy[..., 0] - b2_xy[..., 0]) ** 2
center_squared_h = (b1_xy[..., 1] - b2_xy[..., 1]) ** 2
center_squared_diag = center_squared_w + center_squared_h
eiou = iou - center_squared_w / enclose_squared_w - center_squared_h / enclose_squared_h - center_squared_diag / enclose_squared_diag
return 1-eiou
⚪ SIoU Loss
SIoU包括交并比、角度损失、距离损失和形状损失。角度损失衡量两个边界框的水平或垂直夹角,距离损失衡量两个边界框的中心距离,形状损失衡量两个边界框长宽之间的差异。
\[\begin{aligned} \text{SIoU} &= IoU - \frac{\Delta + \Omega}{2} \\ \Lambda &= 1-2 \cdot \sin^2 \left( \arcsin(x) - \frac{\pi}{4} \right) \\ \Delta &= \sum_{t=x,y} (1-e^{-\gamma \rho_t}) \\ \Omega &= \sum_{t=w,h} (1-e^{-\omega_t})^{\theta} \\ \end{aligned}\]
通过SIoU可以定义SIoU loss:
\[L = 1 - \text{SIoU}\]⚪ MPDIoU loss
MPDIoU直接最小化预测边界框与实际标注边界框之间的左上角和右下角点距离。
\[\text{MPDIoU} = \text{IoU} - \frac{d_1^2}{w^2+h^2}- \frac{d_2^2}{w^2+h^2}\]
通过MPDIoU可以定义MPDIoU loss:
\[\text{MPDIoU loss} = 1-\text{MPDIoU}\]6. 目标检测中的标签分配策略
标签分配(label assignment, LA)策略是指在训练目标检测器时,为特征图不同位置的预测样本分配合适的标签(即区分anchor是正样本还是负样本),用于计算损失。标签分配根据非负即正划分为硬标签分配(hard LA)和软标签分配(soft LA)。
- 硬标签分配策略是指根据阈值把样本划分为正样本或者负样本。依据在训练阶段是否动态调整阈值,硬标签分配策略又可以细分为静态和动态两种:
- 静态分配策略主要依据于模型的先验知识(例如距离阈值和iou阈值等)来选取不同的正负样本;
- 动态分配策略依据在训练阶段采用不同的统计量来动态地设置阈值,并划分正负样本;如DLA, MCA, HAMBox, ATSS, SimOTA, DSLA。
- 软标签分配策略则会根据预测结果与GT计算正负权重,在候选正样本(中心点落在GT框内)的基础上依据正负样本权重分配正负样本,且在训练的过程中动态调整分配权重。常见的软标签分配策略包括Noisy Anchor, AutoAssign, SAPD, TOOD。
(1)静态分配策略
⚪ Anchor-based的静态分配策略
Anchor-based的静态分配策略是基于IoU阈值来实现的,通过计算预测框和GT之间的交并比来划分正负样本;常应用在Faster RCNN、YOLO等网络中。流程如下:
- 初始化时假设每个anchor的mask都是$-1$,表示都是忽略anchor
- 计算每个anchor和所有GT的IoU,把最大IoU小于neg_iou_thr的anchor的mask设置为$0$,表示负样本(背景样本)
- 把最大IoU大于pos_iou_thr的anchor的mask设置为$1$,表示该anchor负责预测该gt bbox,是正样本
- 可能会出现某些GT没有分配到对应的anchor,因此对于每个GT还需要找出最大IoU的anchor位置,如果其IoU大于min_pos_iou,将该anchor的mask设置为$1$,表示该anchor负责预测该GT
在该分配策略中,每个anchor最多只能预测一个GT,而每个GT可能由多个anchor负责预测;IoU介于neg_iou_thr和pos_iou_thr之间的anchor可能被忽略。
# overlaps 表示anchor与gt的交并比矩阵
# 1. 所有index全部设置为-1,表示忽略anchor
assigned_gt_inds = overlaps.new_full((num_bboxes),
-1,
dtype = torch.long)
# 计算每个anchor和哪个gt的iou最大
max_overlaps, argmax_overlaps = overlaps.max(dim=0)
# 计算每个gt和哪个anchor的iou最大
gt_max_overlaps, gt_argmax_overlaps = overlaps.max(dim=1)
# 2. 对于每个anchor,如果其和gt的最大iou小于阈值neg_iou_thr,则分配负样本
assigned_gt_inds[(max_overlaps >= 0)
& (max_overlaps < neg_iou_thr)] = 0
# 3. 对于每个anchor,如果其和gt的最大iou大于阈值pos_iou_thr,则分配负样本
pos_inds = max_overlaps >= pos_iou_thr
assigned_gt_inds[pos_inds] = argmax_overlaps[pos_inds] + 1
# 4. 对于每个gt,如果其和anchor的最大iou大于阈值min_pos_iou,则分配正样本
for i in range(num_gts):
if gt_max_overlaps[i] >= min_pos_iou:
assigned_gt_inds[gt_argmax_overlaps[i]] = i + 1
⚪ Anchor-free的静态分配策略
Anchor-free的静态分配策略是基于距离阈值来实现的。以FCOS模型为例,将输入图像上的位置作为anchor point的中心点,并且对这些anchor point进行回归。
- 由于Anchor-free方法通常是多尺度预测输出,因此需要首先考虑GT由哪一个输出层具体负责。首先设计min_size和max_size来确定某个GT到底由哪一层负责,比如设置$0, 64, 128, 256, 512$和无穷大,则第1层负责预测尺度在0~64范围内的GT,第2层负责预测尺度在64~128范围内的GT,其余类推。通过该分配策略就可以将不同大小的GT分配到最合适的预测层进行学习。
- 然后需要确定在每个输出层上面,哪些空间位置是正样本区域,哪些是负样本区域。采用center sampling来确定正负样本,具体是:引入了center_sample_radius(基于当前stride参数)的参数用于确定在半径范围内的样本都属于正样本区域,其余区域作为负样本。默认配置center_sample_radius=1.5,以第1层为例,其stride=8,在该输出层上基于gt bbox中心点为起点,在半径为1.5*8=12个像素范围内都属于正样本区域。
(2)动态分配策略
⚪ Dynamic Label Assignment (DLA)
IoU阈值$T_{now}$动态调整,做法是首先计算每个ROI和所有GT的最大IoU值,在每张图片上选取第$K_{I-th}$个最大值,遍历所有图片求均值作为$T_{now}$,并且每隔$C$个迭代更新一次该参数。
⚪ Minimum Cost Assignment (MCA)
在进行标签匹配时,同时考虑分类损失和位置损失,对每个GT只有一个具有最小分类损失和定位损失的样本被分配为正样本。
⚪ Online High-quality Anchors Mining (HAMBox)
HAMBox在保证IoU质量的前提下,尽可能保证每个GT都有指定数目的$K$个anchor进行匹配(并没有保证一定要$K$个)。
- 将每个GT匹配到IoU大于阈值的anchor,如果匹配到$K$个正样本,则不需要补充;否则假设只匹配到$M$个正样本;
- 在每次前向传播之后,每个anchor通过回归得到回归框$B_{reg}$;对每个未匹配完成的GT计算它与$B_{reg}$的IoU值,然后补偿$K-M$个unmatched anchor:
- IoU要大于阈值$T$
- 对上一步得到的anchor进行排序,选择IoU最大的top-(K-M)个anchor做补偿。
⚪ Adaptive Training Sample Selection (ATSS)
ATSS根据检测框中心的L2距离和IoU阈值自适应地选择正负样本:
- 针对每个GT,在每个尺度的特征图上计算预测框与GT的$l_{2}$距离,选取其中最小的前$k$(默认为$9$)个作为候选正样本;
- 计算每个GT和候选正样本的IoU值,并统计这些IoU值的均值和方差;
- 对均值和方差求和,并将该值作为划分正负样本的阈值:大于该值的候选正样本为最终正样本,反之就是负样本。
⚪ SimOTA
SimOTA基于代价矩阵和IoU,在训练的过程中动态选择正负样本:
- 将落在GT框内的特征点作为候选正样本;
- 计算候选正样本与GT的分类交叉熵和回归损失,两值相加即为代价矩阵的元素值;
- 计算GT和候选正样本的IoU值,并对计算出的IoU值进行排序,选取前$k$个值(默认为$16$)进行相加,该值作为最终划分正样本的个数值$k_{2}$;
- 针对每个GT,选择代价矩阵最小的$k_{2}$个候选正样本作为最终的正样本,其余的为负样本。分配到多个GT的预测框取选取最小代价的进行匹配。
⚪ Dynamic Soft Label Assigner (DSLA)
Dynamic Soft Label Assigner主要包括使用位置先验信息损失、样本回归损失、样本分类损失,同时对三个损失进行了 Soft 处理进行参数调优, 以达到最佳的动态匹配效果。
位置先验信息损失:
\[C_{center} = \alpha^{|x_{pred}-x_{gt}|-\beta}\]样本回归损失:
\[C_{reg} = -\log(IOU)\]样本分类损失:
\[C_{cls} = CE(P,Y_{soft}) *(Y_{soft}-P)^2\]通过计算上述三个损失的和得到最终的 cost_matrix 后, 再使用 SimOTA 决定每一个 GT 匹配的样本的个数并决定最终的样本。具体操作如下所示:
- 首先通过自适应计算每一个 GT 要选取的样本数量: 取每一个 GT 与所有 bboxes 前 13 大的 IoU, 得到它们的和取整后作为这个 GT 的 样本数目 , 最少为 1 个, 记为 dynamic_ks。
- 对于每一个 GT , 将其 cost_matrix 矩阵前 dynamic_ks 小的位置作为该 GT 的正样本。
- 对于某一个 bbox, 如果被匹配到多个 GT 就将与这些 GTs 的 cost_marix 中最小的那个作为其 label。
(3)软标签分配策略
⚪ Noisy Anchor
Noisy Anchor对每个GT根据IoU分别选出TOP-N样本分别作为候选正样本$A_{pos}$和候选负样本$A_{neg}$,并为其设置软标签:
\[c = \begin{cases} \alpha\cdot \text{loc_a} + (1-\alpha)\cdot \text{cls_c}, & b \in A_{pos} \\ 0, & b \in A_{neg} \end{cases}\]loc_a表示定位置信度,采用预测box和对应的GT之间的IOU衡量;cls_c表示分类置信度,通过网络head直接预测。对于候选正样本$A_{pos}$,进一步引入了损失函数的软权重:
\[r = \left( \alpha\cdot f(\text{loc_a}) + (1-\alpha)\cdot f(\text{cls_c}) \right)^\gamma\]⚪ AutoAssign
AutoAssign基于预测框的分类得分、框回归得分、中心先验得分计算正负权重,实现对GT框内物体的形状自适应,以及不同FPN层物体正负样本的自动划分:
- 所有FPN特征点落在GT框内的作为候选正样本,其余的作为负样本;
- 针对负样本,其负样本属性权重为$1$,正样本属性权重为$0$;而针对候选正样本,其负样本属性权重计算方式为分类得分乘以前背景得分,而正样本属性权重来自于分类得分、前背景得分和IoU得分,以及综合考虑中心先验得分;
- 计算损失时考虑所有样本的负权重和候选正样本的正权重

⚪ Soft Anchor-Point Detection (SAPD)
SAPD首先设计了一个和检测器联合训练的元选择(meta-selection)网络,它为每个GT预测各个特征金字塔level的软选择权重。然后对于正样本anchor point,会根据anchor point到对应目标中心点的距离以及它所属的特征金字塔level的软选择权重两个因素来调整该anchor point对整个网络损失的影响权重。

⚪ Task-aligned One-stage Object Detection (TOOD)
针对分类回归任务解耦所带来的空间不一致问题(即要求正样本高置信度高定位,负样本低置信度低定位),TOOD设计出一种预测框的度量方式,对预测框进行正负样本的划分:
- 所有候选点落在GT框内即为候选正样本;
- 针对每个GT,计算其与候选正样本的IoU值$u$,并与其置信度得分$s$相乘后作为度量值$t=s^\alpha\times u^\beta$;
- 根据$t$排序选择前$k$个候选正样本作为最终的正样本;
- 如果一个预测框和多个GT进行匹配,则选择IoU最大的GT。


