AutoAssign:密集目标检测中的可微标签分配.
标签分配(Label Assignment) 主要是指检测器在训练阶段区分正负样本并给特征图的每个位置赋予合适的学习目标的过程。它是目标检测所必须的一个步骤,标签分配的结果直接决定了模型的学习目标,进而决定了模型性能的好坏。
在早期的 YOLO 中,只需要考虑单个 scale 的 空间维度的 assign 问题,但是随着 FPN 被广泛采用,标签分配开始需要额外解决不同大小的 gt 如何选择合适的 scale 的问题。常见的标签分配方法存在如下特点:
- 在 prior 层面:现有标签分配方法都利用了中心先验,也就是说都依赖于 “物体在 bounding box 中的分布大致是围绕框的中心的”。如果存在一个不符合中心先验的数据集, 现有标签分配方法会失效。
- 在 Instance 层面:现有的标签分配方法在遵循中心先验的前提下,通过各自的方式解决了物体在 scale 维度和 spatial 维度的分配。
- 存在的问题:
- 现有的标签分配方法,在给定一个边界框$(x, y, w, h)$后,无论框内是什么物体,其标签分配的结果已经基本确定了(某些动态方法可以缓解这一点)。
- 有海量的超参数需要调整:例如 anchor 的数量、尺寸、长宽比;或者半径,top-k,IoU 阈值等等。
- 现有的标签分配方法对 spatial 和 scale 的 assign 是分别采用不同的方式解决的。
为了更好的理清标签分配的问题,本文首先尝试去掉了所有的标签分配规则,得到了一个(可能是)最简单的标签分配策略VanillaDet。VanillaDet 是指对于一个 gt box,所有在这个 gt box 内的位置(所有 FPN 层都包含在内)都是这个 gt 的正样本;反之所有不落在 gt 框内部的位置都是负样本。
虽然 VanillaDet 的性能很差(主要是因为不同大小的物体的正样本数量极不均衡导致),但VanillaDet解决了海量超参数和spatial 与 scale不同步的问题。因此 VanillaDet 可能是一个后续研究标签分配问题的一个具有潜力的起点。
VanillaDet仍然存在两个问题:
- 无法保证中心先验
- 由于 gt 框内所有位置都会被当作正样本,这导致了大物体的正样本个数会变得特别多,进一步导致了大小物体、FPN 层间正样本个数不均衡的问题;除此之外,也会出现正负样本的比例失调的问题
在 AutoAssign 中,分别通过 Center Weighting 和 Confidence Weighting 解决了上面这两个问题。
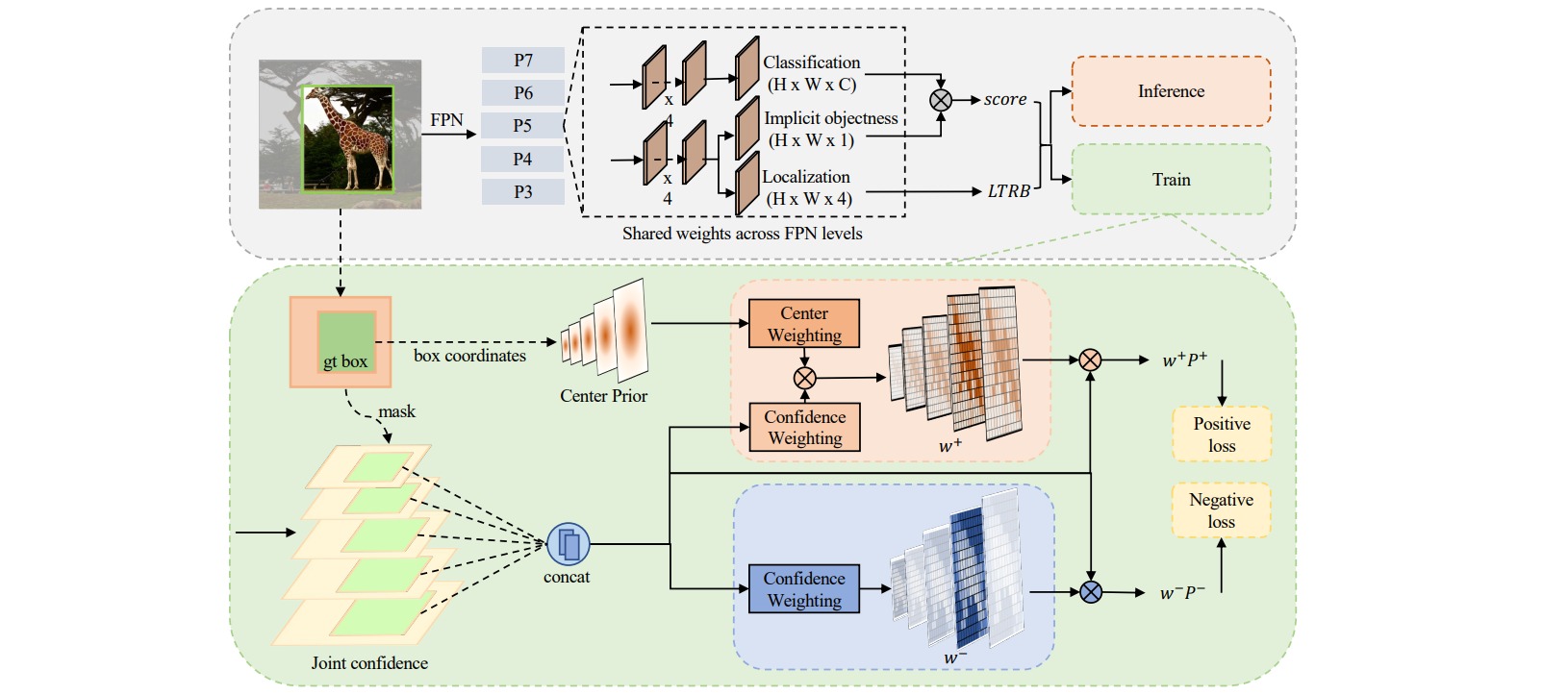
1. Center Weighting
虽然中心先验是标签分配能够 work 的前提,但现实世界的物体 instance 分布是多种多样的,可能不满足中心区域包含物体这一条件。如果对于这些有特定形状的物体,能够自适应的调整中心先验的分布可能会更好,因此引入了高斯中心先验 Gaussian Center Prior 如下:
\[G(d\mid \mu,\sigma) = e^{\frac{-(d-\mu)^2}{2\sigma^2}}\]高斯中心先验是一个关于 location offset $d$ 的函数,直观上说,一个位置距离 gt box 的中心点越远,它的重要性就越低。除此之外,对于每个类别,赋予了一个 $\mu$ 和 $\sigma$ 参数,通过其与 confidence 的相互作用,逐渐自适应到类别特定的 pattern。
2. Confidence Weighting
正样本中,不仅涵盖了所有可能的前景点,同时引入了大量的背景。为了缓解 VanillaDet 引入的大量背景位置,重新 refine 了 classification 的定义,AutoAssign 引入了一个 Implicit-objectness 的分支:
\[P_i(cls\mid \theta) = P_i(cls \mid obj,\theta)P_i(obj\mid \theta)\]Implicit-objectness 分支的作用如下:
- ImpObj 结合 localization 分支,可以看作是一个 RPN 网络。localization 分支可以通过 ImpObj 来调整 classification 分支的预测结果。
- 手动 sample 正样本的过程,可以看作是手动定义 $P(obj\mid \theta)$ 的过程,是一个非 $0$ 即 $1$ 的 hard mask。而在 AutoAssign 中,$P(obj\mid \theta)$ 变成了一个 soft mask。

直观上判断前背景,不仅仅需要考虑分类,回归也是很重要的衡量标准。因此,在 AutoAssign 中,首先将 cls 和 loc 通过简单的变换结合到了一起:
\[\begin{aligned} \mathcal{L}_i(\theta) & =\mathcal{L}_i^{c l s}(\theta)+\lambda \mathcal{L}_i^{l o c}(\theta) \\ & =-\log \left(\mathcal{P}_i(\operatorname{cls} \mid \theta)\right)+\lambda \mathcal{L}_i^{l o c}(\theta) \\ & =-\log \left(\mathcal{P}_i(\operatorname{cls} \mid \theta) e^{-\lambda \mathcal{L}_i^{l o c}(\theta)}\right) \\ & =-\log \left(\mathcal{P}_i(\operatorname{cls} \mid \theta) \mathcal{P}_i(\operatorname{loc} \mid \theta)\right) \\ & =-\log \left(\mathcal{P}_i(\theta)\right) \end{aligned}\]得到能够综合衡量 cls 和 loc 的 $P$ 之后,引入 Confidence Weighting:
\[C(P_i) = e^{\frac{P_i(\theta)}{\tau}}\]3. AutoAssign
AutoAssign 通过 Center Weighting $G$ 和 Confidence Weighting $C$ 构造正负样本权重:
\[\begin{aligned} w_i^+ &= \frac{C(P_i)G(d_i)}{\sum_{j \in S_n}C(P_j)G(d_j)} \\ w_i^- &= 1-f\left( \frac{1}{1-iou_i} \right) \end{aligned}\]对于前景和背景的 weighting function,有一个共同的特点是 “单调递增”;也就是说,一个位置预测 pos / neg 的置信度越高,那么他们当多前景 / 背景的权重就越大。
对于一个前景位置,需要满足 center prior,所以在计算 positive weight 时,需要结合 Guassian Center Weighting;而背景的分布不做任何假设。
另一方面,由于前景点和背景点需要执行的 task 不同(前景需要 cls、obj 和 localization;背景只需要 cls 和 obj),而一个框内的 location 更倾向于相信它是前景,因此对于负样本区域只采用了基于 IoU 的加权。
有了对于正负样本的权重之后,对于一个 gt box,其 loss 如下:
\[\mathcal{L}_n(\theta) = -\log \left(\sum_{i \in S_n}w_i^+P_i^+\right) - \sum_{i \in S_n}\log \left(w_i^-P_i^-\right)\]


