Convolutional Neural Networks.

卷积神经网络(Convolutional Neural Networks, CNN)是一种为计算机视觉任务设计的深度网络，其结构设计灵感来自Hubel和Wiesel的工作，因此在很大程度上遵循了灵长类动物视觉皮层的基本结构。

卷积神经网络的学习过程与灵长类动物的视觉皮层腹侧通路(V1-V2-V4-IT/VTC)非常相似。灵长类动物的视觉皮层首先从视网膜位区域接收输入，在该区域通过外侧膝状核执行多尺度高通滤波和对比度归一化。然后通过分类为V1,V2,V3和V4的视觉皮层的不同区域执行检测。实际上视觉皮层的V1和V2部分类似于卷积层和下采样层，而颞下区类似于更深的层，最终对图像进行推断。

典型的卷积神经网络结构如图所示，通常是由卷积层、激活函数和池化层堆叠构成，用于从图像中自适应地提取特征图(feature map)，并进一步用于下游任务中。其中激活函数用于增强网络的非线性表示能力，池化层用于特征的空间尺寸下采样。本文主要介绍卷积神经网络中的卷积层。

1. 卷积神经网络中的卷积层

卷积层(convolutional layer)的目的是从输入图像中提取对下游任务有用的特征。卷积层的基本单位是卷积核(kernel)，也叫滤波器(filter)。

在传统图像处理方法中，图像滤波器算子通常是人工设计的，比如通过高斯滤波器可以进行噪声过滤，通过Sobel算子进行轮廓提取等等。而卷积层中的滤波器参数是从数据集中学习得到的，可以根据下游任务自适应地学习到最合适的参数。

卷积神经网络中的卷积层实际上是一种局部的互相关(Cross-Correlation)操作，相对于数学定义的卷积缺少对卷积核进行翻转的步骤。而翻转是为了使卷积运算满足可交换性，由于卷积层的参数是自动学习的，(如果需要)也可以学习到翻转的参数，因此没有必要显式地进行翻转。

(1) 卷积层的计算

卷积层是一种局部操作，下面以二维卷积为例。假设输入图像(或特征图) $X\in \Bbb{R}^{H \times W \times C}$，其中$H,W$是图像的高度和宽度，$C$是图像的通道(channel)数（对于输入图像指代颜色通道，对于特征图指代深度）。

对于一个卷积核$K \in \Bbb{R}^{f \times f \times C}$，在图像上按照光栅扫描顺序(raster scanning order)滑动。当滑动到空间点$p_0$时，该点的输出值通过局部仿射变换计算：

\[y(p_0) = \sum_{p_n \in \mathcal{R}} w(p_n) \cdot x(p_0+p_n) + b\]

其中$\mathcal{R} = [-\lfloor\frac{f}{2}\rfloor,…,\lfloor\frac{f}{2}\rfloor] \times [-\lfloor\frac{f}{2}\rfloor,…,\lfloor\frac{f}{2}\rfloor]$。因此一个卷积核共有$f \times f \times C+1$个参数(权重+偏置)。

卷积层还具有步长(stride)参数和填充(padding)参数。步长是指卷积核在图像上进行一次滑动时所移动的像素数量，步长$s>1$会导致特征图的空间尺寸变小；填充参数是指在图像的四周填充像素，具有三种模式：

若输入图像尺寸为$n\times n\times c$，使用卷积核的尺寸为$f\times f\times c$，步长为$s$，填充为$p$，则单个卷积核对应的输出特征的尺寸是：

\[\lfloor \frac{n+2p-f}{s}\rfloor +1 \times \lfloor\frac{n+2p-f}{s}\rfloor +1\]

通常认为一个卷积核只捕捉输入图像中的一种特定的局部特征。因此通过使用多个卷积核提取包含不同语义信息的特征，其中每个卷积核对应输出特征的一个通道。

下图给出了一个步长为$2$、填充为$1$的$3 \times 3$卷积核的示意图：

可以通过torch.nn.Conv2d在Pytorch中定义二维卷积层：

conv_layer = torch.nn.Conv2d(
    in_channels,  # 输入图像/特征的通道数量
    out_channels, # 输出特征的通道数量(所使用的卷积核数量)
    kernel_size,  # 卷积核的空间尺寸
    stride=1, padding=0, # 步长和填充参数
    dilation=1, groups=1, # 实现空洞卷积和组卷积
    bias=True, # 是否使用偏置项
    padding_mode='zeros', # 填充模式，可选'zeros', 'reflect', 'replicate', 'circular'
    device=None, dtype=None)

(2) 卷积层的特点

⚪ 局部连接 (local connection)

全连接神经网络中的神经元与上一层的所有神经元连接，参数量较大；而卷积层的输出特征中的每一个元素都只和上一层特征对应位置的局部邻域内的元素相连，构成一个局部连接网络。

⚪ 参数共享 (parameter sharing)

参数共享是指卷积层的每一个卷积核在特征的不同位置上是共享参数的。参数共享能够进一步减少卷积层的参数量，此时每一个卷积核可以提取具有某种固定模式的特征(比如水平线段或竖直线段)，通过使用复数个卷积核能够提取不同语义信息的特征。

⚪ 平移等变性 (translation equivariance)

平移变换是指把一幅图像或一个空间中的每一个点沿相同方向移动相同的距离。平移等变性是指对输入进行平移变换时，系统在不同位置的工作原理相同，但它的响应随着目标位置的变化而变化。对于卷积层，输入图像经过平移后，输出特征图上的对应特征表达也是平移的。

进一步地，如果卷积层之后应用池化层、全连接层等结构，则整个网络具有平移不变性(translation invariance)。此时无论目标出现在图像中的哪个位置，它都会检测到相同的特征，输出同样的响应。

(3) 卷积层的感受野

卷积层的特征提取能力可以用感受野(receptive field)衡量。感受野定义为每一层输出特征上的像素点对应输入图像上的区域大小。第$n$层卷积层的感受野计算为第$n$层输出特征图中的一个像素对应输入图像的像素数。

令网络第$n$层卷积层的卷积核大小为$f_n$，步长参数为$s_n$。则第$n$层卷积层的感受野$RF_n$可以递归地计算为：

\[RF_n = RF_{n-1} + (f_{n}-1)*\prod_{i=1}^{n-1} {s_i}\]

第$n$层特征的每个像素对应第$n-1$层特征的$f_n$个像素，其中中间像素具有相对于输入图像的感受野$RF_{n-1}$，而最边缘的像素使得第$n-1$层感受野相对于第$n-2$层增大了$(f_{n}-1)s_{n-1}$，递归地等价于相对于输入图像增大了$(f_{n}-1)\prod_{i=1}^{n-1} {s_i}$。

下面给出了一个应用步长为$2$的$3 \times 3$卷积层堆叠两层的感受野情况。则第一层卷积层具有$3 \times 3$的感受野；第二层卷积层相对于第一层卷积层具有$3 \times 3$的感受野，相对于输入图像扩展了$(3-1)*2$个像素。

在构建卷积神经网络时，通常采用更小的卷积核堆叠更多层数来实现较大的感受野，以减少网络参数量。比如两层$3\times 3$的卷积层和一层$5\times 5$的卷积层具有相同的感受野，但前者的参数量更小（$2*3^2<5^2$）：

⭐扩展阅读：

2. 不同类型的卷积层

卷积神经网络中的卷积层包括标准卷积, 转置卷积, 扩张卷积(Dilated Conv, IC-Conv), 可分离卷积(空间可分离卷积, 深度可分离卷积, 平展卷积), 组卷积, 可变形卷积, 差分卷积(中心差分卷积, 交叉中心差分卷积, 像素差分卷积), 动态卷积(CondConv, DynamicConv, DyNet, ODConv, DRConv), Involution, 圆形卷积, 八度卷积, 稀疏卷积(空间稀疏卷积, 子流形稀疏卷积), CoordConv。

(1) 转置卷积 Transposed Convolution

转置卷积 (Transposed Convolution)也叫解卷积(Deconvolution)，能够对特征图的空间尺寸进行上采样，把低维特征映射到高维特征。

转置卷积是通过自动地对输入特征进行full填充实现的。若输入图像的空间尺寸为$n\times n$，设置$f\times f$的转置卷积核，则会自动对输入特征填充$f-1$层零像素，从而使得卷积核滑动的初始位置恰好与原图像的一个像素点相交，保证特征提取过程是有意义的。此时输出特征的空间尺寸为：

\[n' = n+(f-1)\]

下图给出了通过一个$3\times 3$转置卷积把$2\times 2$特征转换成$4\times 4$特征的过程。

在转置卷积中，也可以人为地设置填充参数$p$。当设置填充参数$p>0$时，相当于指定输入特征的最外$p$层为填充像素，此时特征的有效尺寸为$n-2p$，$f\times f$的转置卷积核所产生的输出特征的空间尺寸为：

\[n' = n+(f-1)-2p\]

填充参数$p$相当于转置卷积核自动对输入特征填充的零像素层数减少$p$层。下图给出了通过一个填充为$p=1$的$3\times 3$转置卷积把$5\times 5$特征转换成$5\times 5$特征的过程。

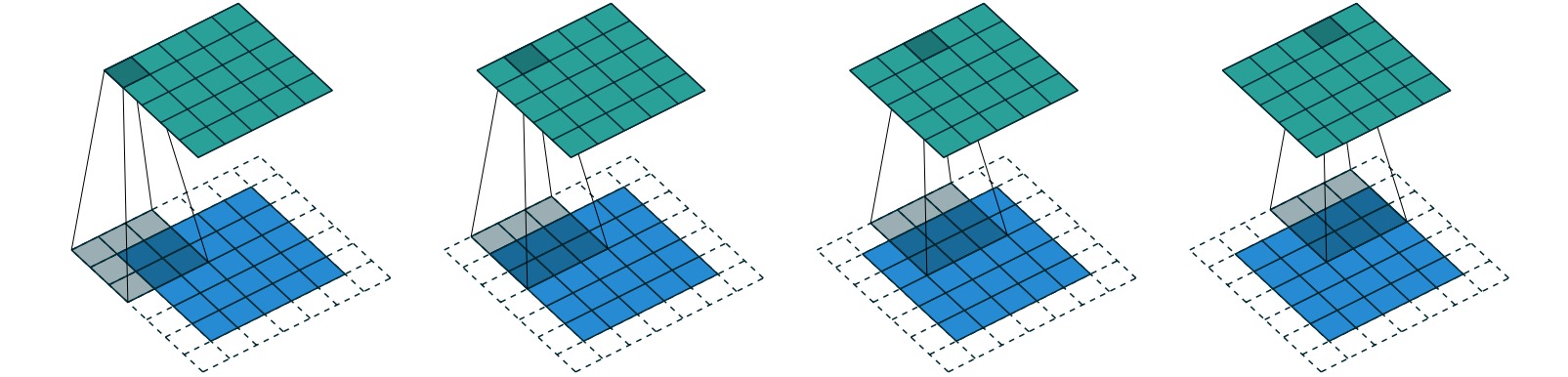
转置卷积也可以设置步长参数$s$ (实现上采样的主要参数)。步长参数$s>1$相当于对输入特征的相邻像素之间插入$s-1$个空洞，对应的卷积也叫做微步长卷积 (Fractionally-Strided Convolution)，此时输入特征的空间尺寸等效为$s(n-1)+1$，$f\times f$的转置卷积核对应的输出特征的空间尺寸为：

\[n' = s(n-1)+1+(f-1) = s(n-1) + f\]

下图给出了通过一个步长为$s=2$的$3\times 3$转置卷积把$2\times 2$特征转换成$5\times 5$特征的过程。

综上所述，若输入图像尺寸为$n\times n\times c$，使用$c’$个尺寸为$f\times f\times c$的卷积核，步长为$s$，填充为$p$，输出图像尺寸为$n’\times n’\times c’$，则存在如下关系：

\[n' = s(n-1) + f -2p\]

可以通过torch.nn.ConvTranspose2d在Pytorch中定义二维转置卷积层：

deconv_layer = torch.nn.ConvTranspose2d(
    in_channels,  # 输入图像/特征的通道数量
    out_channels, # 输出特征的通道数量(所使用的卷积核数量)
    kernel_size,  # 卷积核的空间尺寸
    stride=1, padding=0, # 步长和填充参数
    bias=True, # 是否使用偏置项
    )

⚪ 转置卷积的由来

在计算机内的卷积操作是通过矩阵运算实现的(im2col)。把输入特征展平为列向量，把卷积核转换为一个稀疏矩阵。通过稀疏矩阵和列向量的矩阵乘法可以得到输出列向量，再调整为输出尺寸即可：

若对卷积核对应的稀疏矩阵进行转置，再与输出列向量做矩阵乘法，则可以得到与原始输入相同形状的向量。值得一提的是，由于稀疏矩阵并不是正交矩阵，因此转置之后的矩阵乘法并不能恢复到原始的数值，而是仅仅保留原始的形状，即上述的两次操作并不具备可逆关系。这也是转置矩阵的由来。

⚪ 棋盘效应

使用转置卷积时会出现棋盘效应(Checkboard Artifact)，即图像中会出现棋盘格状的伪影。这是因为转置卷积中通常设置步长$s>1$，当卷积核大小$f$不能被步长$s$整除时，转置卷积的计算会不均匀重叠，使图像中某个部位的颜色比其他部位更深。

下面以一维转置卷积为例说明棋盘效应。对于卷积核尺寸为$2 \times 2$、步长为$2$的转置卷积，输入特征中的一个像素会映射到输出特征上连续的两个像素并且之间没有重叠。当卷积核尺寸调整为$3 \times 3$时，每一个输入像素映射到输出特征的三个像素区域，且之间会有重叠。这会导致输出特征上的每个像素接收的信息量与相邻像素不同，从而产生棋盘效应。

一些避免棋盘效应的做法：

(2) 扩张卷积 Dilated Convolution

扩张卷积 (Dilated Convolution)也称为膨胀卷积、空洞卷积 (Atrous Convolution)，能够在不增加参数数量的前提下增大网络的感受野。

扩张卷积引入了膨胀/扩张率(Dilation Rate) $d$。扩展率$d$是指在卷积核的相邻元素之间插入$d-1$个空洞；当$d=1$时扩张卷积退化为标准的卷积。

对于尺寸为$f\times f$的扩张卷积核，若扩张率为$d$，则等效为$f’=d(f-1)+1$的标准卷积核，对应的输出特征的空间尺寸是(步长为$s$，填充为$p$)：

\[n' = \lfloor \frac{n+2p-f'}{s}\rfloor +1\]

下图给出了一个使用扩张率$d=2$的$3 \times 3$扩张卷积处理空间尺寸为$7 \times 7$的输入特征的例子，得到$3 \times 3$的输出特征。

扩张卷积通过等效地增大卷积核尺寸，使网络具有更大的感受野，但没有额外增加卷积核的参数量。

扩张卷积存在的问题包括：

可以通过torch.nn.Conv2d中的dilation参数构建扩张卷积：

conv_layer = torch.nn.Conv2d(
    in_channels,  # 输入图像/特征的通道数量
    out_channels, # 输出特征的通道数量(所使用的卷积核数量)
    kernel_size,  # 卷积核的空间尺寸
    stride=1, padding=0, # 步长和填充参数
    dilation=1,   # 扩张卷积的扩张率
    bias=True, # 是否使用偏置项
    padding_mode='zeros', # 填充模式，可选'zeros', 'reflect', 'replicate', 'circular'
    device=None, dtype=None)

⚪ Inception Convolution (IC-Conv)

IC-Conv独立定义每个轴、每个通道和每个卷积层的扩张率，提供了一个密集的有效感受野范围。

\[d = \{ d_x^i,d_y^i \mid d_x^i,d_y^i \in 1,2,...,d_{\max},i=1,2,...,C^{out} \}\]

通过高效的扩张搜索算法，在预训练超网络时每一层卷积核核覆盖了所有可能的扩张率，并通过最小化原始卷积层的输出与裁剪出来的扩张卷积的L1误差来选择扩张率。

(3) 可分离卷积 Separable Convolution

⚪ 空间可分离卷积 Spatially Separable Convolution

空间可分离卷积 (Spatially Separable Convolution)是指把$f \times f$的卷积核分解成两个独立的卷积核$f \times 1$和$1 \times f$，然后分别对图像的高度方向和宽度方向进行操作。

空间可分离卷积能够有效地降低卷积的计算成本。对于$f \times f$的卷积核，若特征的空间尺寸为$n \times n$且在计算过程中没有改变，并且不考虑偏置项，则标准卷积和空间可分离卷积的参数量和计算量分别为：

  标准卷积 空间可分离卷积 比值
参数量(Params) $f \times f$ $f \times 1 + 1 \times f$ $\frac{2}{f}$
乘加运算量(Mult-Adds) $(n \times n) \times (f \times f)$ $(n \times n) \times (f \times 1) + (n \times n) \times (1 \times f)$ $\frac{2}{f}$

深度学习中通常很少使用空间可分离卷积，这是因为并非所有卷积核都可以拆分成两个较小的卷积核，强制拆分则会阻碍在训练期间搜索所有可能的卷积核。

⚪ 深度可分离卷积 Depthwise Separable Convolution

深度可分离卷积 (Depthwise Separable Convolution)是由深度(Depthwise)卷积和逐点(Pointwise)卷积构成的。

深度卷积是指对输入特征图的每一个通道使用一个单通道卷积核进行处理，从而实现通道独立、空间交互的卷积操作。逐点卷积是指对输入特征图的每一个空间位置使用一个1×1卷积核进行处理，从而实现空间独立、通道交互的卷积操作。

深度可分离卷积是深度学习中常用的降低计算成本的卷积层。对于$f \times f\times c$的卷积核，若特征的空间尺寸为$n \times n$且在计算过程中没有改变，并且不考虑偏置项，共采用$c’$个卷积核，则标准卷积和深度可分离卷积的参数量和计算量分别为：

  标准卷积 深度卷积 逐点卷积 比值
参数量(Params) $c’ \times (f \times f\times c)$ $c \times (f \times f \times 1)$ $c’ \times (1 \times 1\times c)$ $\frac{1}{c’}+\frac{1}{f^2}$
乘加运算量(Mult-Adds) $(n \times n\times c’) \times (f \times f\times c)$ $(n \times n\times c) \times (f \times f\times 1)$ $(n \times n\times c’) \times (1 \times 1\times c)$ $\frac{1}{c’}+\frac{1}{f^2}$

深度可分离卷积大幅度减少卷积的参数，其主要缺点是对于规模较小的模型，模型容量可能会显著降低，拟合能力变弱，训练得到的模型可能是次优的。

深度可分离卷积可以通过torch.nn.Conv2d实现：

class DSConv(nn.Module):
    def __init__(self, in_channels, out_channels):
        super().__init__()
        self.depthwise_separable_conv = nn.Sequential(
            torch.nn.Conv2d(in_channels, in_channels, kernel_size=3, padding=1, groups=in_channels),
            torch.nn.Conv2d(in_channels, out_channels, kernel_size=1, padding=0),
        )

    def forward(self, x):
        return self.depthwise_separable_conv(x)

⚪ 平展卷积 Flattened Convolution

平展卷积 (Flattened Convolution)通过把卷积核分别沿着通道维度和两个空间维度分离，显著地减少了卷积的计算成本。这种分离假设是卷积核为rank-1张量，从而可以分解为三个一维向量。

(4) 组卷积 Grouped Convolution

组卷积 (Grouped Convolution)把输入特征沿通道维度分成$g$个组，对每个组分别应用标准的卷积操作。

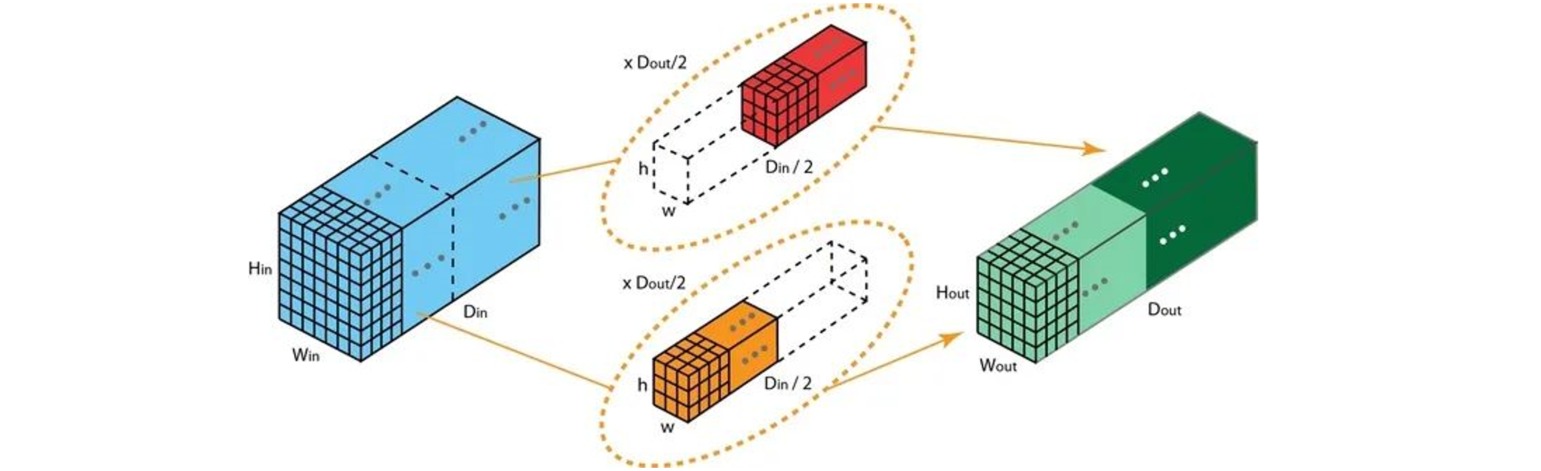
组卷积的主要优点包括：

可以通过torch.nn.Conv2d中的groups参数构建组卷积：

conv_layer = torch.nn.Conv2d(
    in_channels,  # 输入图像/特征的通道数量
    out_channels, # 输出特征的通道数量(所使用的卷积核数量)
    kernel_size,  # 卷积核的空间尺寸
    stride=1, padding=0, # 步长和填充参数
    groups=1,   # 组卷积的分组数
    bias=True, # 是否使用偏置项
    padding_mode='zeros', # 填充模式，可选'zeros', 'reflect', 'replicate', 'circular'
    device=None, dtype=None)

(5) 可变形卷积 Deformable Convolution

可变形卷积(Deformable Convolution)是指在使用卷积核对输入特征图上的局部区域进行加权平均时，对输入特征的每个空间位置增加偏移项$\Delta p_n$：

\[y(p_0) = \sum_{p_n \in \mathcal{R}} w(p_n) \cdot x(p_0+p_n+\Delta p_n)\]

可变形卷积具有任意形状的感受野。当尺寸为$k \times k$的可变形卷积核作用于中心位置$p_0$的局部特征时，通过标准卷积学习$2k^2$个偏移项(分别控制水平和垂直方向的偏移)。偏移项的学习结果为浮点数，因此通过双线性插值计算其对应的像素值。

Deformable Convolution v2进一步对每个偏移位置$\Delta p_n$额外学习一个偏移权重$\Delta m_n \in [0,1]$，用于评估该特征位置的重要性程度。$\Delta m_n$是由数据学习得到的，因此不能与卷积核权重$w(p_n)$合并。

\[y(p_0) = \sum_{p_n \in \mathcal{R}} w(p_n) \cdot x(p_0+p_n+\Delta p_n) \cdot \Delta m_n\]

(6) 差分卷积 Difference Convolution

差分卷积 (Difference Convolution)起源于局部二值模式 (Local Binary Pattern, LBP)。LBP定义在图像的3×3邻域内，以中心像素为阈值，将相邻$8$个像素的灰度值与其进行差分比较：若大于中心像素值被标记为$1$，否则为$0$；可产生$8$位二进制数（通常转换为十进制数即LBP码，共$256$种），即得到该中心像素点的LBP值，并用这个值来聚合邻域内的差分信息。

差分卷积则是用卷积处理输入图像或特征的差分信息，能较好地描述细粒度的纹理信息，经常应用在纹理识别、人脸识别、边缘检测等领域。

中心差分卷积 (Central difference convolution, CDC)是指对邻域特征进行中心差分，计算过程可以分解为标准卷积和中心差分项：

\[\begin{aligned} y(p_0) &= \sum_{p_n \in \mathcal{R}} w(p_n) \cdot [x(p_0+p_n)-x(p_0)] \\ &= \sum_{p_n \in \mathcal{R}} w(p_n) \cdot x(p_0+p_n)-x(p_0) \cdot \sum_{p_n \in \mathcal{R}} w(p_n) \end{aligned}\]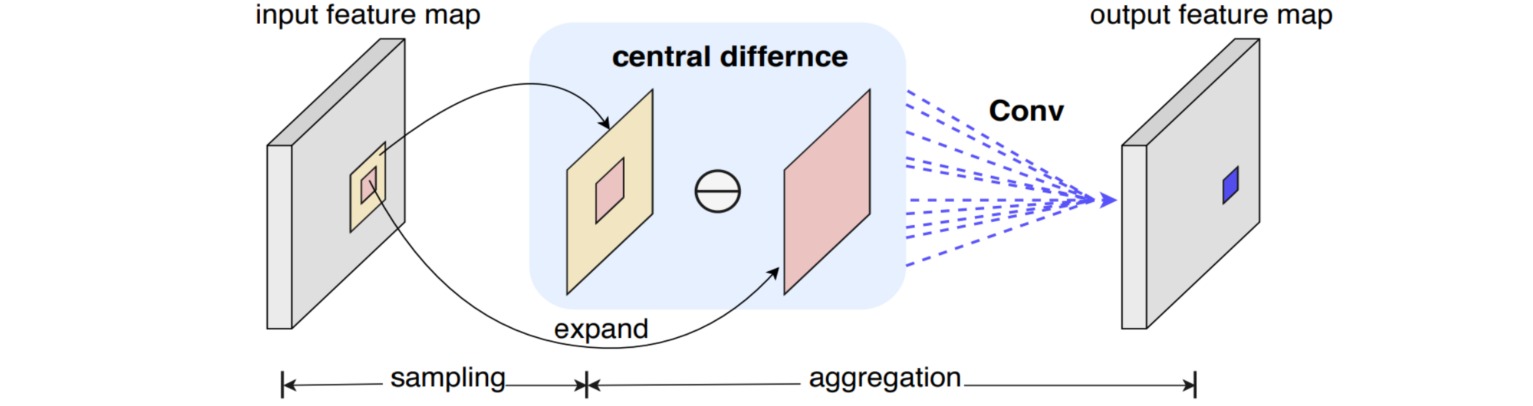

交叉中心差分卷积 (Cross-CDC)把CDC解耦成水平垂直和对角线两个对称交叉的子算子，以减少对所有邻域特征都进行差分操作带来的较大的冗余。

像素差分卷积 (Pixel difference convolution, PDC)则聚合了对邻域特征进行中心差分、对邻域进行顺时针方向的两两差分、以及对更大感受野的5x5邻域进行外环与内环差分。

7. 动态卷积 Dynamic Convolution

动态卷积是指把多个卷积核线性加权为一个动态核$w(\cdot)=\sum_{k=1}^K \pi_k(x)w_k(\cdot)$，而权重$\pi_k$则与输入$x$有关，因此动态卷积核具有数据依赖性。

\[\begin{aligned} y(p_0) &= \sum_{p_n \in \mathcal{R}} (\sum_{k=1}^K \pi_k(x)w_k(p_n)) \cdot x(p_0+p_n) \end{aligned}\]

⚪ 条件参数化卷积 (Conditionally Parameterized Convolution, CondConv)

CondConv通过通道注意力机制(全局平均池化+全连接层+Sigmoid函数)构造卷积核的权重 $0\leq \pi_k(x) \leq 1$。

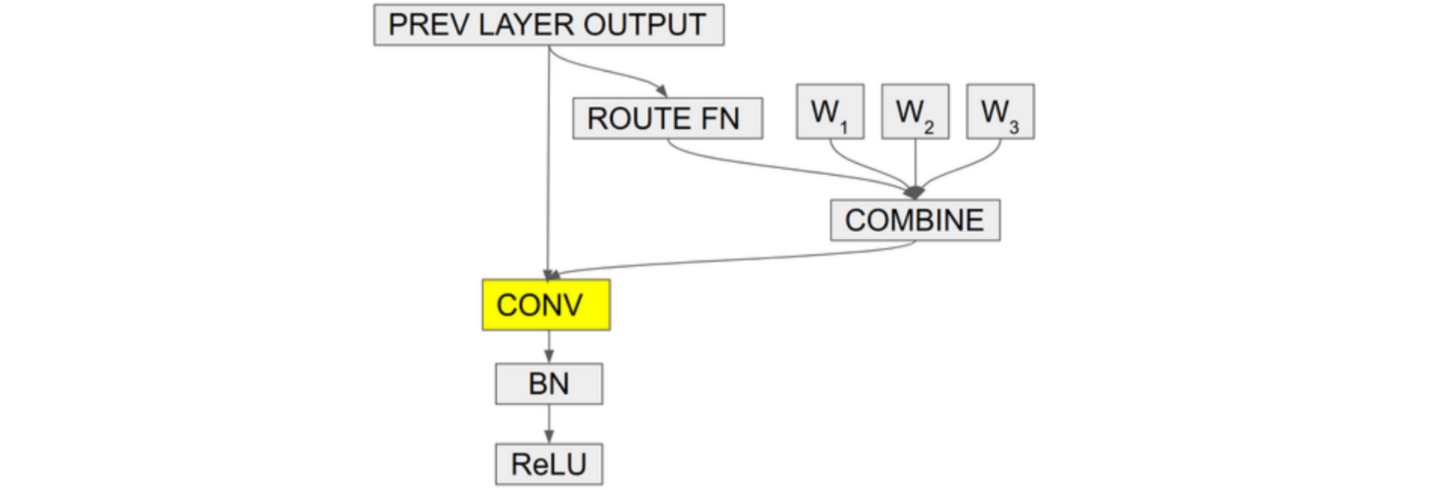
⚪ DynamicConv

DynamicConv采用平滑注意力的方式生成卷积核权重。

\[\pi_k=\frac{\exp(z_k/\tau)}{\sum_j \exp(z_j/\tau)} \quad \text{s.t. } 0\leq \pi_k(x) \leq 1,\sum_{k=1}^K \pi_k(x)=1\]

⚪ DyNet

DyNet的实现过程与CondConv类似，主要区别在于核融合过程是分别在每个输出通道上进行的。若特征的输出通道数为$C_{out}$，对每个输出通道应用$K$个卷积核，则权重向量$\pi$的长度为$KC_{out}$。

⚪ 全维动态卷积 (Omni-Dimensional Dynamic Convolution, ODConv)

ODConv把融合卷积核的注意力机制扩展为多维形式：标量注意力$\alpha_w \in \Bbb{R}^{K}$对$K$个整体卷积核赋予不同的注意力值；空间注意力$\alpha_s \in \Bbb{R}^{f \times f}$对每个卷积核的不同空间位置赋予不同的注意力值；输入通道注意力$\alpha_c \in \Bbb{R}^{c_{in}}$对每个卷积核的不同输入通道赋予不同的注意力值；输出通道注意力$\alpha_f \in \Bbb{R}^{c_{out}}$对不同输出通道的卷积核赋予不同的注意力值。

⚪ 动态区域感知卷积 (Dynamic Region-Aware Convolution, DRConv)

DRConv通过卷积核生成模块根据输入图片动态生成每个区域对应的卷积核，通过可学习的引导掩码模块把不同卷积核分配到不同的特征区域。

8. Involution

标准的卷积操作具有两个特点：空间参数共享和通道参数独立。空间参数共享是指在不同的空间位置共享卷积核，有助于捕捉与空间位置无关的视觉特征；通道参数独立是指是指卷积在不同通道具有不同的值，用于收集不同的语义信息。

Involution则是一种空间参数独立、通道参数共享的卷积核；空间参数独立使得卷积核能在不同空间位置适应不同的视觉模式，通道参数共享能够减少通道间冗余的影响。对于输入像素$p_0$，Involution通过非线性函数$\phi(\cdot)$ (全局平均池化+带瓶颈层的全连接层)构造卷积核$w(p_0)=\phi(p_0)\in \Bbb{R}^{f \times f\times 1}$，然后对局部特征加权求和。

9. 圆形卷积 Circle Convolution

圆形卷积的设计受生物视觉系统的感受野启发，通过各向同性的感受野适应全局或者局部输入特征在不同方向上的信息变化。圆形卷积可以看作是一种特殊的可变形卷积，而可变形卷积引入额外的参数和计算量，增加了计算复杂度；圆形卷积则通过对特征的双线性插值构造，由于双线性插值是一种线性变换，因此可以通过重参数技巧与卷积的权值矩阵合并；在推理时直接使用新的卷积核进行常规卷积操作。

10. 八度卷积 Octave Convolution (OctConv)

卷积层的特征图中存在高、低频分量。其中低频分量支撑的是图像的整体特征，是存在冗余的，在编码过程中可以节省。Octave Convolution首先构造图像特征图的线性尺度表示：把原始特征的$1-\alpha$通道看作高频分量，剩余$\alpha \in [0,1]$通道经过$t=2$的高斯滤波后作为低频分量。由于低频分量是冗余的，因此把低频分量的空间尺寸设置为高频分量空间尺寸的一半。

由于高/低频特征的空间尺寸不一致，把标准卷积的卷积核$W \in \Bbb{R}^{c_{in}\times c_{out} \times f \times f}$拆分成四部分：$W^{H→H},W^{L→L},W^{L→H},W^{H→L}$实现不同频率分量内部的更新和相互交互。$W^{H→H},W^{L→L}$处理的特征尺寸不变，因此采用标准卷积操作；$W^{H→L}$先对特征进行平均池化，再执行标准卷积；$W^{L→H}$则是先执行标准卷积，再对特征进行空间上采样。

\[\begin{aligned} y^H(p_0)& = \sum_{p_n \in \mathcal{R}} w^{H→H}(p_n) \cdot x^H(p_0+p_n) \\&+ \sum_{p_n \in \mathcal{R}} w^{L→H}(p_n) \cdot x^L(\lfloor \frac{p_0}{2} \rfloor +p_n) \\ y^L(p_0)& = \sum_{p_n \in \mathcal{R}} w^{L→L}(p_n) \cdot x^L(p_0+p_n) \\&+ \sum_{p_n \in \mathcal{R}} w^{H→L}(p_n) \cdot x^H(2 p_0+0.5 +p_n) \end{aligned}\]

11. 稀疏卷积 (Sparse Convolution)

对于稀疏的输入图像，如三维点云体素，其中存在大量的空白区域(像素为$0$)，此时使用卷积操作滑动扫描所有像素将会产生大量的无效计算量。

稀疏卷积 (Sparse Convolution)只对输入图像/特征中的非零像素进行卷积操作，从而实现了稀疏数据的高效计算。把输入图像中的非零像素称为active input site，则稀疏卷积具有两种形式：

稀疏卷积的实现过程如下，首先根据输入和输出特征构建哈希表(Hash Table)。对于输入图像中的每一个非零像素$P_{in}$，根据其对应输入图像中的坐标位置$key_{in}$和顺序编号$v_{in}$构建输入哈希$Hash_{in}$；然后对每一个非零的输入像素$P_{in}$计算其所有能影响到的输出特征像素$P_{out}$，根据对应输出特征中的坐标位置$key_{out}$和顺序编号$v_{out}$构建输出哈希$Hash_{out}$。

然后根据输入和输出哈希建立规则手册(Rule Book)，把稀疏卷积中所有的原子计算(atomic operation)关联到对应的卷积核元素上，从而把卷积转换为有效的可编程形式。

对于任意输入像素$P_{in}$，对应的每一个输出像素$P_{out}$是通过卷积核中某个元素与输入相乘得到的，因此记录卷积核中对应的偏置坐标$(i,j)$。根据偏置坐标$(i,j)$建立规则手册，分别记录每个坐标元素使用的次数$count$，对应的输入像素编号$v_{in}$和输出像素编号$v_{out}$。

根据输入和输出哈希表以及规则手册可以实现稀疏卷积计算。首先根据规则手册查询卷积核的每个元素$(i,j)$作用的输入像素编号$v_{in}$以及对应的输出像素编号$v_{out}$，根据输入像素编号$v_{in}$对应的输入像素坐标$key_{in}$上的像素值构建稀疏的输入张量，并与卷积核元素对应相乘后把结果累积到输出像素编号$v_{out}$对应的输出像素坐标$key_{out}$上。

12. CoordConv

卷积层具有平移等变性，在进行坐标变换时存在缺陷，比如无法将笛卡尔空间中的坐标表示转换为one-hot像素空间中的坐标。CoordConv通过显式地为特征图添加位置编码后再送入卷积，从而提升卷积层进行数值回归能力。