Generative Adversarial Networks.

本文目录：

  1. 理解生成对抗网络：博弈论视角、优化视角、能量模型视角、动力学视角
  2. 使用Pytorch实现生成对抗网络：MMGAN、NSGAN、合并交替优化
  3. 生成对抗网络的评估指标：KDE、IS、FID、KID
  4. 生成对抗网络的训练困难：纳什均衡、低维流形、梯度消失、模式崩溃
  5. 生成对抗网络的各种变体：改进目标函数、改进网络结构、改进优化过程、其他应用

1. 理解生成对抗网络

生成对抗网络(Generative Adversarial Network, GAN)是一种生成模型，可以用来生成图像、文本、语音等结构化数据(structured data)。

假设真实数据具有概率分布\(P_{data}(x)\)，GAN使用一个生成器generator构造真实分布的一个近似分布\(P_G(x)\)，并使用一个判别器discriminator衡量生成分布和真实分布之间的差异。

对于判别器$D$，希望其能正确地区分真实数据与生成数据。若输入数据来自真实分布\(P_{data}\)，则希望其输出结果接近$1$；反之若数据来自生成分布$P_G$，则希望其输出结果接近$0$。优化目标采用二元交叉熵：

\[D^* = \mathop{\arg \max}_{D} \Bbb{E}_{x \text{~} P_{data}(x)}[\log D(x)] + \Bbb{E}_{z \text{~} P_{Z}(z)}[\log(1-D(G(z)))]\]

对于生成器$G$，希望其能够成功地欺骗判别器，使其将生成样本误分类成真实样本：

\[G^* = \mathop{\arg \min}_{G} \Bbb{E}_{z \text{~} P_{Z}(z)}[\log(1-D(G(z)))]\]

⚪ 从博弈论视角理解生成对抗网络

若将判别器$D$和生成器$G$的目标函数合并，记为：

\[\begin{aligned} \mathop{ \min}_{G} \mathop{\max}_{D} L(G,D) & = \Bbb{E}_{x \text{~} P_{data}(x)}[\log D(x)] + \Bbb{E}_{z \text{~} P_{Z}(z)}[\log(1-D(G(z)))] \\ & = \Bbb{E}_{x \text{~} P_{data}(x)}[\log D(x)] + \Bbb{E}_{x \text{~} P_{G}(x)}[\log(1-D(x))] \end{aligned}\]

上式表示判别器$D$和生成器$G$在进行极小极大博弈(minimax game)：这也是一个零和博弈(zero-sum game)，参与博弈的双方，在严格竞争下，一方的收益必然意味着另一方的损失，博弈各方的收益和损失相加总和永远为“零”。 在交替迭代的过程中，双方都极力优化自己的网络，从而形成竞争对抗，直到双方达到纳什均衡 (Nash equilibrium)。

观察目标可知博弈过程旨在寻找使得判别器$D$造成的损失$L(G,D)$最大值最小的生成器$G$。

⚪ 从优化视角理解生成对抗网络

将目标函数写成积分形式：

\[\begin{aligned} L(G,D) & = \Bbb{E}_{x \text{~} P_{data}(x)}[\log D(x)] + \Bbb{E}_{x \text{~} P_{G}(x)}[\log(1-D(x))] \\ & =\int_x (P_{data}(x)\log D(x) + P_{G}(x)\log(1-D(x))) dx \end{aligned}\]

下面先求判别器$D$的最优值$D^{*}$，注意到积分不影响最优值的取得，因此计算被积表达式的极值\(\frac{\partial L(G,D)}{\partial D} = 0\)，得：

\[D^*(x) = \frac{P_{data}(x)}{P_{data}(x)+P_{G}(x)} \in [0,1]\]

若生成器$G$也训练到最优值，此时有\(P_{data}(x)≈P_{G}(x)\)，则判别器退化为常数 $D^{*}(x)=\frac{1}{2}$，失去判别能力。

当判别器$D$取得最优值$D^{*}$时，目标函数为：

\[\begin{aligned} L(G,D^*) & =\int_x (P_{data}(x)\log D^*(x) + P_{G}(x)\log(1-D^*(x))) dx \\ & =\int_x (P_{data}(x)\log \frac{P_{data}(x)}{P_{data}(x)+P_{G}(x)} + P_{G}(x)\log\frac{P_{G}(x)}{P_{data}(x)+P_{G}(x)}) dx \\ & =\int_x (P_{data}(x)\log \frac{P_{data}(x)}{\frac{P_{data}(x)+P_{G}(x)}{2}} + P_{G}(x)\log\frac{P_{G}(x)}{\frac{P_{data}(x)+P_{G}(x)}{2}}-2\log 2) dx \\ & = 2D_{JS}[P_{data}(x) || P_G(x)]-2\log 2 \end{aligned}\]

其中$D_{JS}$表示JS散度。因此当判别器$D$取得最优时，GAN的损失函数衡量了真实分布\(P_{data}(x)\)与生成分布\(P_G(x)\)之间的JS散度。若生成器$G$也取得最优值，则损失函数取得最小值 $-2\log 2$。

另一方面，传统的基于极大似然估计(maximum likelihood estimation)的生成模型本质上是在最小化真实分布\(P_{data}(x)\)与生成分布\(P_G(x)\)之间的KL散度：

\[\begin{aligned} \mathop{ \max}_{G} L(G) & = \Bbb{E}_{x \text{~} P_{data}(x)}[\log P_G(x)] = \int_x P_{data}(x)\log P_G(x) dx \\ & = \int_x P_{data}(x)\log \frac{P_G(x)}{P_{data}(x)} dx + \int_x P_{data}(x)\log P_{data}(x) dx \\ & = -D_{KL}[P_{data}(x) || P_G(x)] + Const. \end{aligned}\]

由于JS散度相比于KL散度具有对称性、平滑性等优点，因此通常认为GAN相比于传统的生成模型能够取得更好的表现。

值得一提的是，GAN的目标函数只有先精确完成\(\mathop{\max}_{D}\)，然后再进行\(\mathop{ \min}_{G}\)，才相当于优化两个分布的JS散度；在实际训练时常采用交替优化步骤，即先优化判别器再优化生成器，并且判别器的更新次数通常更多一些(或使用的学习率更大一些)；这样做的目的也是为了让判别器先取得局部最优，从而让生成器的优化过程趋近于JS散度的最小化过程(但理论上不可能精确逼近分布度量)。

⚪ 从能量模型视角理解生成对抗网络

能量模型是指使用如下能量分布拟合一批真实数据$x_1,x_2,\cdots,x_n$~\(P_{data}(x)\)：

\[q_{\theta}(x) = \frac{e^{-U_{\theta}(x)}}{Z_{\theta}},Z_{\theta} = \int e^{-U_{\theta}(x)}dx\]

其中$U_{\theta}(x)$是带参数的能量函数；$Z_{\theta}$是配分函数(归一化因子)。直观地，真实数据分布在能量函数中势最小的位置。我们希望通过对抗学习使得生成数据$\hat{x}_1,\hat{x}_2,\cdots \hat{x}_n$的势也尽可能小。

使用判别器$D(x)$拟合能量函数$U_{\theta}(x)$，使用生成器构造生成分布$P_G(x)$。根据能量模型的正相-负相分解构造目标函数：

\[D^* \leftarrow \mathop{ \min}_{D} \Bbb{E}_{x \text{~} P_{data}(x)} [ D(x)]- \Bbb{E}_{x \text{~} P_G(x)}[D(x) ]\]

上式表示判别器的目标为最小化真实数据分布的能量，最大化生成数据分布的能量。

与此同时，生成分布$P_G(x)$与能量分布$q_{\theta}(x)$应该足够接近，使用KL散度衡量两者差异：

\[\begin{aligned} D_{KL}[P_G(x) || q_{\theta}(x)] &= \int P_G(x) \log \frac{P_G(x)}{q_{\theta}(x)} dx \\ &= \int P_G(x) \log P_G(x) dx - \int P_G(x) \log q_{\theta}(x) dx \\ &= -H(G(z))+\Bbb{E}_{x \text{~} P_G(x)}[D(x) ] + \log Z_{\theta} \end{aligned}\]

上式第一项$H(G(z))$表示生成样本的熵，希望熵越大越好(对应样本多样性越大)；第二项表示生成样本的势能，希望势越小越好(接近真实样本)；第三项是一个常数。通过上式可以构造生成器的目标函数：

\[G^* \leftarrow \mathop{ \min}_{G} -H(G(z))+\Bbb{E}_{x \text{~} P_G(x)}[D(x) ]\]

上式表示生成器的目标为最小化生成数据分布的能量，并最大化生成数据分布的熵。

⚪ 从动力学视角理解生成对抗网络

GAN的学习过程为交替优化以下目标函数：

\[\begin{aligned} \mathop{ \min}_{\theta_G} \mathop{\max}_{\theta_D} L(\theta_G,\theta_D) & = \Bbb{E}_{x \text{~} P_{data}(x)}[\log D(x;\theta_D)] + \Bbb{E}_{z \text{~} P_{Z}(z)}[\log(1-D(G(z;\theta_G);\theta_D))] \end{aligned}\]

若学习算法采用梯度下降算法，则上式对应一个由常微分方程组ODEs表示的动力学系统：

\[\begin{pmatrix} \dot{\theta}_D \\ \dot{\theta}_G \end{pmatrix}= \begin{pmatrix} \nabla_{\theta_D} L(\theta_G,\theta_D) \\ -\nabla_{\theta_G} L(\theta_G,\theta_D) \end{pmatrix}\]

通过对上述ODEs的分析，可以了解GAN的以下性态：

2. 使用Pytorch实现生成对抗网络

⚪ GAN的算法流程

初始化生成器$G(z;\theta_G)$和判别器$D(x;\theta_D)$，在训练的每一次迭代中，先更新判别器$D$，再更新生成器$G$：

\[θ_D \leftarrow \mathop{\arg \max}_{\theta_D} \frac{1}{n} \sum_{i=1}^{n} {\log D(x^i)} + \frac{1}{n} \sum_{i=1}^{n} {\log (1-D(\tilde{x}^i))}\] \[\theta_G \leftarrow \mathop{\arg \min}_{\theta_G} \frac{1}{n} \sum_{i=1}^{n} {\log (1-D(\tilde{x}^i))}\]

上述即为GAN的标准训练流程，采用该流程的GAN也被称作Minimax GAN (MMGAN)。

⚪ 从MMGAN到NSGAN

由于上式在计算$θ_G$时，函数$\log (1-D(x))$在$D(x)$接近$0$（即训练的初始阶段）时梯度较小，在$D(x)$接近$1$（即优化后期）时梯度较大，会造成优化困难；因此在实践中采用下式代替：

\[\theta_G \leftarrow \mathop{\arg \max}_{\theta_G} \frac{1}{n} \sum_{i=1}^{n} {\log D(\tilde{x}^i)}\]

使用上式的GAN被称作Non-saturating GAN (NSGAN)。

⚪ GAN的Pytorch实现

import torch

# 定义生成器和判别器
generator = Generator()
discriminator = Discriminator()

# 定义损失函数
adversarial_loss = torch.nn.BCELoss()

# 定义优化器
optimizer_G = torch.optim.Adam(generator.parameters(), lr=0.0002, betas=(0.5, 0.999))
optimizer_D = torch.optim.Adam(discriminator.parameters(), lr=0.0002, betas=(0.5, 0.999))

for epoch in range(n_epochs):
    for i, real_imgs in enumerate(dataloader):
        # 构造对抗标签
        valid = torch.ones(real_imgs.shape[0], 1).requires_grad_.(False)
        fake = torch.zeros(real_imgs.shape[0], 1).requires_grad_.(False)

        # 从噪声中采样生成图像
        z = torch.randn(real_imgs.shape[0], latent_dim)
        gen_imgs = generator(z)

        # 训练判别器
        optimizer_D.zero_grad()
        # 计算判别器的损失
        real_loss = adversarial_loss(discriminator(real_imgs), valid)
        fake_loss = adversarial_loss(discriminator(gen_imgs.detach()), fake) # 此处不计算生成器的梯度
        d_loss = (real_loss + fake_loss) / 2
        # 更新判别器参数
        d_loss.backward()
        optimizer_D.step()

        # 训练生成器
        optimizer_G.zero_grad()
        g_loss = adversarial_loss(discriminator(gen_imgs), valid)
        g_loss.backward()
        optimizer_G.step()

⚪ 技巧：合并交替优化

GAN的训练过程采用交替优化的形式：

\[\begin{aligned} D^* &\leftarrow \mathop{ \max}_{D} \Bbb{E}_{x \text{~} P_{data}(x)}[\log D(x)] + \Bbb{E}_{z \text{~} P_z}[\log(1-D(G(z)))] \\ G^* & \leftarrow \mathop{ \max}_{G} \Bbb{E}_{z \text{~} P_z}[\log D(G(z))] \end{aligned}\]

如果能把交替优化步骤合并为一个步骤，则可以节省优化所需的时间（代价是增大优化过程占用的显存）。

合并交替优化的关键是引入stop gradient操作（对应pytorch中的.detach()方法）。

对于判别器，目标是优化判别器的参数，因此把生成器的梯度置零：

\[\begin{aligned} D^* \leftarrow \mathop{ \max}_{D} \Bbb{E}_{x \text{~} P_{data}(x)}[\log D(x)] + \Bbb{E}_{z \text{~} P_z}[\log(1-D(\text{StopGrad}(G(z))))] \end{aligned}\]

对于生成器，目标时优化生成器的参数。注意到反向传播中$D(G(z))$会产生生成器和判别器的联合梯度$(\nabla_G L,\nabla_D L)$，而生成器梯度置零后\(\text{StopGrad}(D(G(z)))\)会产生判别器的梯度$(0,\nabla_D L)$；两者作差即为生成器的梯度：

\[\begin{aligned} G^* & \leftarrow \mathop{ \max}_{G} \Bbb{E}_{z \text{~} P_z}[\log D(G(z))-\log D(\text{StopGrad}(G(z)))] \end{aligned}\]

值得一提的是，上述形式的生成器目标数值将恒为零，然而梯度不为零；此时生成器损失不宜再作为指示训练过程的指标，但是参数更新过程仍然在正常进行。

因此GAN的目标函数可以合并写作：

\[\begin{aligned} (D^*, G^*) \leftarrow \mathop{ \max}_{D,G} & \Bbb{E}_{x \text{~} P_{data}(x)}[\log D(x)] + \Bbb{E}_{z \text{~} P_z}[\log(1-D(\text{StopGrad}(G(z))))] \\ &+ \lambda \Bbb{E}_{z \text{~} P_z}[\log D(G(z))-\log D(\text{StopGrad}(G(z)))] \end{aligned}\]

其中$\lambda$控制判别器和生成器的学习率之比为$1:\lambda$。至此GAN的更新过程可以被合并为一步：

# 定义优化器
optimizer = torch.optim.Adam(
    itertools.chain(generator.parameters(), discriminator.parameters()), 
    lr=0.0002, betas=(0.5, 0.999)
)

for epoch in range(n_epochs):
    for i, real_imgs in enumerate(dataloader):
        # 构造对抗标签
        valid = torch.ones(real_imgs.shape[0], 1).requires_grad_.(False)
        fake = torch.zeros(real_imgs.shape[0], 1).requires_grad_.(False)

        # 从噪声中采样生成图像
        z = torch.randn(real_imgs.shape[0], latent_dim)
        gen_imgs = generator(z)

        # 构造损失函数
        d_real_loss = adversarial_loss(discriminator(real_imgs), valid)
        d_fake_loss = adversarial_loss(discriminator(gen_imgs.detach()), fake) # 此处不计算生成器的梯度
        d_loss = (d_real_loss + d_fake_loss) / 2
        g_fake_loss = adversarial_loss(discriminator(gen_imgs), valid)
        g_fake_loss_sg = adversarial_loss(discriminator(gen_imgs.detach()), valid) # 此处不计算生成器的梯度
        g_loss = (g_fake_loss - g_fake_loss_sg) / 2
        loss = d_loss + lambda * g_loss

        # 更新网络参数
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

3. 生成对抗网络的评估指标

GAN的训练过程是交替迭代的，其目标函数值无法直观地给出生成器和判别器的训练程度，使得GAN的训练过程不知何时停止，也不方便对不同模型的性能进行比较。

由于无法直接建立真实数据和生成数据之间的一一对应关系，因此需要为GAN设计有效的评估指标，用于评估真实数据分布和生成数据分布之间的“距离”。 本节介绍几种GAN的评估指标：

⚪ Kernel Density Estimation (KDE)

从生成器$G$中随机采样一些样本，使用高斯混合模型拟合这些样本，得到生成样本分布的估计$P_G$；选择一些真实样本$x^i$，计算其在估计分布中的极大似然概率：

\[L = \frac{1}{N} \sum_{i=1}^{N} {\log (P_G(x^i))}\]

将这个似然值作为GAN模型质量的评估指标。这种评估方法存在一些问题，比如模型可能产生不同于已知样本集的高质量样本；也可能存在一些低质量样本的似然值较高。

⚪ Inception Score (IS)

Inception Score借助图像分类任务评估生成图像的质量。具体地，使用Inception模型对生成图像$x$进行分类，得到类别标签$y$；则IS定义如下：

\[\begin{aligned} \text{IS}(G) &= e^{\Bbb{E}_{x \text{~} P_G(x)}[D_{KL}(p(y|x)||p(y))]} \\ & ≈ e^{\Bbb{E}_{x \text{~} P_G(x)}[-H[p(y|x)] + H[p(y)]]} \end{aligned}\]

直观地，对于任意一张图像$x$，若其分类标签$p(y|x)$的熵较大，则说明其包含的的主要物体容易被分类，对应图像生成的质量较高；对于所有生成的图像，若平均标签$p(y)$的熵较小，则说明图像类别比较平均，对应图像生成具有多样性。

Inception Score的缺点是没有使用真实世界样本的统计数据；并且依赖于分类任务，比如使用ImageNet数据集训练的Inception评估生成其他数据集的GAN模型是不合适的。

⚪ Fréchet Inception Distance (FID)

FID使用Inception模型的编码层提取数据特征$x$，并假设编码特征服从多维高斯分布，通过Fréchet距离 (也称为Wasserstein-2距离) 衡量真实数据特征和生成数据特征的差异。

记真实特征分布$P_{data}(x)$为$N(\mu,\Sigma)$，生成特征分布$P_G(x)$为$N(\mu_G,\Sigma_G)$，则两个分布之间的FID定义为：

\[\text{FID}(P_{data}(x),P_G(x))= ||\mu-\mu_G||_2^2+\text{Tr}(\Sigma+\Sigma_G-2(\Sigma\Sigma_G)^{1/2})\]

⚪ Kernel Inception Distance (KID)

KID定义为在Inception模型提取的特征空间中的最大平均差异：

\[\begin{aligned} \text{KID}(P_{data}(x),P_G(x))=& \Bbb{E}_{x,x' \text{~} P_{data}(x)} [\kappa(x,x')] + \Bbb{E}_{x,x' \text{~} P_G(x)} [\kappa(x,x')] \\& -2\Bbb{E}_{x \text{~} P_{data}(x),x' \text{~} P_G(x)} [\kappa(x,x')] \end{aligned}\]

相比于FID仅考虑了均值和方差，KID通过核技巧考虑到任意阶数的特征矩。

4. 生成对抗网络的训练困难

众所周知，GAN模型的训练比较困难，训练速度较慢且训练过程不稳定。主要体现在以下几点：

（1）难以实现纳什均衡 Hard to achieve Nash equilibrium

GAN使用梯度下降算法优化两人非合作博弈(non-cooperative)，通常梯度下降算法只有在目标函数为凸函数时才能保证实现纳什均衡。而判别器和生成器独立地优化各自的损失，在博弈中没有考虑到另一方。因此同时更新两个模型的梯度不能保证收敛。

（2）低维流形 Low dimensional manifold

许多真实世界的数据集分布\(P_{data}(x)\)通常集中在高维空间中的一个低维流形上，这是因为真实图像要遵循主题或目标的限制；生成分布\(P_G(x)\)通常也位于一个低维流形上，因为它是由一个低维噪声变量$z$定义的。高维空间中的两个低维流形几乎不可能重叠；即使两个流形有重合的部分，对概率分布采样时也很难采集到重合的样本，从而导致GAN训练的不稳定性。

（3）梯度消失 Vanishing gradient

GAN的训练过程进退两难：如果判别器表现较差，则生成器没有准确的反馈，损失函数不能代表真实情况；如果判别器表现较好，则损失函数及其梯度趋近于$0$，训练过程变得非常慢甚至卡住。

通常GAN的训练过程被视为最优化真实分布与生成分布的f散度(如JS散度)。这类散度在两个概率分布不重叠时始终为常数(或无穷大)，导致更新梯度为$0$。

（4）模式崩溃 Mode collapse

Mode Collapse是指在训练过程中生成器可能会崩溃到一种始终产生相同输出的设置。由于生成器无法学习表示复杂的真实世界数据分布，所学习到的生成分布会陷入一个缺乏多样性的局部空间中，只能集中在真实数据分布的一小部分。

与之类似的一个问题是Mode Dropping，是指真实数据分布通常有多个簇，而生成器的每次迭代过程中只能生成其中某一个簇。

从能量的角度，真实数据分布在能量函数所有可能的极小值点附近。在生成数据时通常只需要找到附近的极小值点；若采用带动量的优化器，则有可能使其跳出附近的极小值点，集中在一些更小的极小值点附近，从而丧失了数据生成的多样性。因此在GAN的优化过程中，尽量使用不带动量的优化器，或者设置较小的动量和学习率。

解决措施①：生成数据的熵约束

Mode Collapse体现在生成数据太集中，因此可以向生成器的目标中加入约束项，使得生成数据更加分散。一种常用的约束是生成数据的熵$H(G(z))$：

\[\begin{aligned} G^* & \leftarrow \mathop{ \max}_{G} \Bbb{E}_{z \text{~} P_z}[\log D(G(z))] + H(G(z)) \end{aligned}\]

解决措施②：GAN的集成

在GAN的训练过程中同时训练多个生成器，每次随机选择一个生成器来生成样本。

5. 生成对抗网络的各种变体

生成对抗网络的设计是集目标函数、网络结构、优化过程于一体的。本节分别从这三个方面介绍GAN的各种变体：

（1）改进目标函数

根据前述分析可知，GAN的判别器$D$定义了真实数据分布\(P_{data}(x)\)与生成数据分布\(P_G(x)\)之间的分布“距离”，生成器$G$的目标函数为最小化两个分布的距离。

对于标准的GAN模型，当判别器$D$取得最优时，其目标函数衡量了两个分布之间的JS散度。对于JS散度，当两个概率分布没有重合时，散度取值通常是固定值，从而导致优化梯度为0。

在实践中可以选择具有更平滑的值空间的分布距离度量指标。常用的距离度量包括分布散度和积分概率度量。

⚪ 基于分布散度的GAN模型

分布散度 $D[p,q]$是关于概率分布$p(x)$和$q(x)$的标量函数，并且满足：

分布散度可以用于衡量两个概率分布的距离，可以通过构造真实数据分布\(P_{data}(x)\)和生成分布\(P_G(x)\)之间的分布散度来设计目标函数。

然而由于分布的形式通常是未知的，因此散度无法直接求解，此时可通过凸函数的共轭函数将散度转化为对偶形式（带$\max$的形式）；进而最小化该散度的对偶形式，从而得到一个$\min$-$\max$过程。

方法 目标函数
Minimax GAN
(MMGAN)		 \(\begin{aligned} \mathop{\min}_{G}\mathop{\max}_{D} \Bbb{E}_{x \text{~} P_{data}(x)}[\log D(x)] + \Bbb{E}_{x \text{~} P_{G}(x)}[\log(1-D(x))] \end{aligned}\)
Non-Saturating GAN
(NSGAN)		 \(\begin{aligned} & \mathop{ \max}_{D} \Bbb{E}_{x \text{~} P_{data}(x)}[\log D(x)] + \Bbb{E}_{x \text{~} P_{G}(x)}[\log(1-D(x))] \\ & \mathop{ \max}_{G} \Bbb{E}_{x \text{~} P_{G}(x)}[\log D(x)] \end{aligned}\)
f-GAN
使用f散度构造目标函数		 \(\begin{aligned} \mathop{\min}_{G} \mathop{\max}_{D \in f'(\Bbb{D})} \Bbb{E}_{x \text{~} P_{data}(x)}[D(x)]- \Bbb{E}_{x \text{~} P_{G}(x)}[f^*(D(x))] \end{aligned}\)
Boundary-Seeking GAN
(BGAN)
边界搜索		 \(\begin{aligned} & \mathop{ \max}_{D} \Bbb{E}_{x \text{~} P_{data}(x)}[\log D(x)] + \Bbb{E}_{x \text{~} P_{G}(x)}[\log(1-D(x))] \\ & \mathop{ \min}_{G} \Bbb{E}_{x \text{~} P_G(x)}[ \frac{1}{2}(\log D(x) - \log (1-D(x)))^2 ] \end{aligned}\)
Softmax GAN
使用Softmax函数构造目标函数		 \(\begin{aligned} & \mathop{ \min}_{D} \frac{1}{|P_{data}|}\Bbb{E}_{x \text{~} P_{data}(x)} [ D(x)] + \log Z_P \\ & \mathop{ \min}_{G} \frac{1}{|P_{data}|+|P_{G}|}(\Bbb{E}_{x \text{~} P_{data}(x)} [ D(x)]+\Bbb{E}_{x \text{~} P_G(x)} [ D(x)] )+ \log Z_P \end{aligned}\)
Relativistic GAN
(RGAN)
相对判别器		 \(\begin{aligned} & \mathop{ \min}_{D} -\Bbb{E}_{x_r \text{~} P_{data}(x), x_f \text{~} P_{G}(x)}[\log \sigma(D(x_r)-D(x_f))] \\ & \mathop{ \min}_{G}- \Bbb{E}_{x_r \text{~} P_{data}(x), x_f \text{~} P_{G}(x)}[\log \sigma(D(x_f)-D(x_r))] \end{aligned}\)
Least Squares GAN
(LSGAN)
使用均方误差构造目标函数		 \(\begin{aligned} & \mathop{ \max}_{D} \Bbb{E}_{x \text{~} P_{data}(x)}[(D(x)-b)^2] + \Bbb{E}_{x \text{~} P_{G}(x)}[(D(x)-a)^2] \\ & \mathop{ \max}_{G} \Bbb{E}_{x \text{~} P_{G}(x)}[(D(x)-c)^2] \end{aligned}\)
Wasserstein Divergence GAN
(WGAN-div)
使用W散度构造目标函数		 \(\begin{aligned} \mathop{ \min}_{G} \mathop{ \max}_{D} \Bbb{E}_{x \text{~} P_{data}(x)}[D(x)]-\Bbb{E}_{x \text{~} P_{G}(x)}[D(x)] - k\Bbb{E}_{x \text{~} r(x)}[ || \nabla_xD(x) ||^p ] \end{aligned}\)
GAN-QP
使用平方势散度构造目标函数		 \(\begin{aligned} & \mathop{ \max}_{D} \Bbb{E}_{x_r \text{~} P_{data}(x), x_f \text{~} P_{G}(x)}[D(x_r,x_f)-D(x_f,x_r) -\frac{(D(x_r,x_f)-D(x_f,x_r))^2}{2 \lambda d(x_r,x_f)} ] \\ & \mathop{ \min}_{G}\Bbb{E}_{x_r \text{~} P_{data}(x), x_f \text{~} P_{G}(x)}[D(x_r,x_f)-D(x_f,x_r)] \end{aligned}\)
Designing GAN
在对偶空间构造目标函数		 \(\begin{aligned} \mathop{ \min}_{G} \mathop{ \max}_{D \in \Omega} \Bbb{E}_{x\text{~}P_{data}(x)}[ \phi(D(x))]+ \Bbb{E}_{x\text{~}P_{G}(x)}[\psi(D(x))] \end{aligned}\)

⚪ 基于积分概率度量的GAN模型

积分概率度量寻找满足某种限制条件的函数集合\(\mathcal{F}\)中的连续函数$f(\cdot)$，然后寻找一个最优的\(f(x)\in \mathcal{F}\)使得两个概率分布$p(x)$和$q(x)$之间的期望差异最大，该最大差异定义为两个分布之间的距离：

\[d_{\mathcal{F}}(p(x),q(x)) = \mathop{\sup}_{f(x)\in \mathcal{F}} \Bbb{E}_{x \text{~} p(x)}[f(x)]-\Bbb{E}_{x \text{~} q(x)}[f(x)]\]
方法 目标函数
Wasserstein GAN
(WGAN)
使用W距离构造目标函数		 \(\begin{aligned} \mathop{ \min}_{G} \mathop{ \max}_{D,|D|_L \leq K} \Bbb{E}_{x \text{~} P_{data}(x)}[D(x)]-\Bbb{E}_{x \text{~} P_{G}(x)}[D(x)] \end{aligned}\)
Wasserstein GAN
gradient penalty
(WGAN-GP)
使用梯度惩罚约束Lipschitz连续性		 \(\begin{aligned} \mathop{ \max}_{D} & \Bbb{E}_{x \text{~} P_{data}(x)}[D(x)]-\Bbb{E}_{x \text{~} P_{G}(x)}[D(x)] \\ & - λ \Bbb{E}_{x \text{~} \epsilon P_{data}(x) + (1-\epsilon)P_{G}(x) }[(|| \nabla_xD(x) || -1)^2] \\ \mathop{ \min}_{G}& -\Bbb{E}_{x \text{~} P_{G}(x)}[D(x)] \end{aligned}\)
DRAGAN
调整梯度惩罚的插值空间		 \(\begin{aligned} \mathop{ \max}_{D} & \Bbb{E}_{x \text{~} P_{data}(x)}[D(x)]-\Bbb{E}_{x \text{~} P_{G}(x)}[D(x)] \\ & - λ \Bbb{E}_{x \text{~} P_{data}(x), \delta \text{~} N(0,cI) }[(|| \nabla_xD(x+\delta) || -k)^2] \\ \mathop{ \min}_{G}& -\Bbb{E}_{x \text{~} P_{G}(x)}[D(x)] \end{aligned}\)
Spectral Normalized GAN
(SN-GAN)
使用谱归一化约束Lipschitz连续性		 \(\begin{aligned} & \mathop{ \max}_{D} \Bbb{E}_{x \text{~} P_{data}(x)}[\max(0,1-D(x))]-\Bbb{E}_{x \text{~} P_{G}(x)}[\max(0,1+D(x))] \\ & \mathop{ \min}_{G} -\Bbb{E}_{x \text{~} P_{G}(x)}[D(x)] \end{aligned}\)
Gradient Normalized GAN
(GN-GAN)
使用梯度归一化约束Lipschitz连续性		 \(\begin{aligned} & \mathop{ \max}_{D} \Bbb{E}_{x \text{~} P_{data}(x)}[D(x)]-\Bbb{E}_{x \text{~} P_{G}(x)}[D(x)] \\ & D^* \leftarrow \frac{D(x)}{||\nabla_x D(x)||+|D(x)|} \\ & \mathop{ \min}_{G} -\Bbb{E}_{x \text{~} P_{G}(x)}[D(x)] \end{aligned}\)
Gradient Normalized GAN v2
(GraN-GAN)
使用梯度归一化约束Lipschitz连续性		 \(\begin{aligned} & \mathop{ \max}_{D} \Bbb{E}_{x \text{~} P_{data}(x)}[D(x)]-\Bbb{E}_{x \text{~} P_{G}(x)}[D(x)] \\ & D^* \leftarrow \frac{D(x) \cdot ||\nabla_x D(x)||}{||\nabla_x D(x)||^2+\epsilon} \\ & \mathop{ \min}_{G} -\Bbb{E}_{x \text{~} P_{G}(x)}[D(x)] \end{aligned}\)
c-transform WGAN
更精确的W距离近似		 \(\begin{aligned} \mathop{ \min}_{G} \mathop{ \max}_{D,|D|_L \leq K} \Bbb{E}_{x \text{~} P_{data}(x)}[D(x)] +\Bbb{E}_{x \text{~} P_{G}(x)}[\mathop{\min}_{\tilde{x} \text{~} P_{data}(x)} \{ c(\tilde{x}-x)- D(\tilde{x})\}] \end{aligned}\)
Mean and Covariance Feature Matching GAN
(McGAN)
均值和协方差特征匹配		 \(\begin{aligned} \mathop{ \min}_{G} \mathop{ \max}_{D} &||\Bbb{E}_{x \text{~} P_{data}(x)}[D(x)]-\Bbb{E}_{x \text{~} P_{G}(x)}[D(x)] ||_p \\ &+ ||\Bbb{E}_{x \text{~} P_{data}(x)}[D(x)D^T(x)]-\Bbb{E}_{x \text{~} P_{G}(x)}[D(x)D^T(x)] ||_{*} \end{aligned}\)
Maximum Mean Discrepancy
(MMD GAN)
最大平均差异		 \(\begin{aligned} & \mathop{ \min}_{G} \mathop{ \max}_{D} \Bbb{E}_{x,x' \text{~} P_{data}(x)} [\kappa(x,x')] + \Bbb{E}_{x,x' \text{~} P_G(x)} [\kappa(x,x')] -2\Bbb{E}_{x \text{~} P_{data}(x),x' \text{~} P_G(x)} [\kappa(x,x')] \\ &\kappa(x,x') = \exp(-||D(x)-D(x')||) \end{aligned}\)
Fisher GAN
Fisher差异		 \(\begin{aligned} \mathop{ \min}_{G} \mathop{ \max}_{D} \frac{\Bbb{E}_{x \text{~} P_{data}(x)}[D(x)]-\Bbb{E}_{x \text{~} P_G(x)}[D(x)]}{\sqrt{\frac{1}{2}(\Bbb{E}_{x \text{~} P_{data}(x)}[D^2(x)]+\Bbb{E}_{x \text{~} P_G(x)}[D^2(x)])}} \end{aligned}\)

（2）改进网络结构

a. 调整神经网络

⚪ Deep Convolutional GAN (DCGAN)

DCGAN使用卷积神经网络构造生成对抗网络，为了稳定卷积网络的训练过程，作者提出了以下几点设计思路：

  1. 去掉网络中的pooling层，在判别器中使用Strided convolution (步幅卷积)进行下采样，在生成器中使用transposed convolution（转置卷积）进行上采样；
  2. 在判别器和生成器中使用batch norm；
  3. 移除网络中的所有全连接层；
  4. 生成器的输出层使用Tanh激活函数，其他层使用ReLU激活函数；
  5. 判别器的所有层使用LeakyReLU激活函数。

⚪ ResNet

为进一步增强卷积网络的非线性表示能力，将ResNet引入了GAN的模型构建。这类网络的主要特点如下：

  1. 由于stride $>1$的卷积操作存在棋盘效应，因此移除了步幅卷积和转置卷积；在下采样时采用平均池化，在上采样时采用线性插值；
  2. 通过增加残差模块的数量，能够同时增加网络的非线性表示能力和深度；
  3. 卷积核设置为$3\times 3$；激活函数统一使用ReLU；BatchNorm可以替换为InstanceNorm等；
  4. 由于GAN的模型初始化通常比较小，将残差形式调整为$x + \alpha f(x); \alpha < 1$具有更好的稳定性。

⚪ Self-Attention GAN (SAGAN)

SAGAN把自注意力机制引入模型结构中，有助于对图像区域中长距离、多层次的依赖关系进行建模。自注意力机制在计算输入位置$i$的特征$y_i$时，考虑所有位置$j$的加权：

\[y_i = \sum_{j}^{} \frac{e^{f(x_i)^Tg(x_j)}}{\sum_j e^{f(x_i)^Tg(x_j)}} h(x_j)\]

SAGAN的输出为$γy + x$，其中$γ$是一个可学习的参数，并且初始化为$0$。网络开始训练时，首先学习局部信息，不采用自注意力模块；随着训练的进行，网络逐渐采用注意力模块学习更多长距离的特征。

⚪ BigGAN

BigGAN整体结构与SAGAN相同，在此基础上采用了更大的数据批量、截断策略和模型稳定性的控制。BigGAN把batch size调整到SAGAN的$8$倍($2048$)；从先验分布$z$采样时，通过设置阈值的方式来截断采样，其中超出范围的采样值被丢弃并重新采样；通过约束权重矩阵的最大奇异值来提高训练稳定性。

⚪ Self-Modulation

自调制模块用于增强训练过程中的稳定性，把生成网络中的BN替换为条件BN，其中仿射参数$\gamma,\beta$是由生成器的输入噪声$z$构造的。

⚪ StyleGAN

StyleGAN采用PGGAN的渐进式学习过程。通过映射网络对隐空间$z$进行特征解耦；通过AdaIN控制不同层级的视觉特征生成；调整常数输入降低生成图像异常；增加噪声输入补充图像细节；通过混合正则化实现视觉特征组合。

⚪ StyleGAN2

StyleGAN2在StyleGAN的基础上通过权重解调制消除了生成图像中的伪影；使用残差网络替换了渐进式学习结构，并增大了高分辨率层中的特征通道数。

⚪ StyleGAN3

StyleGAN3从StyleGAN2的结构出发，从频域角度改进网络结构以实现特征的平移与旋转等变性，消除了生成图像的高频混叠现象。

⚪ Transformer GAN (TransGAN)

TransGAN使用Transformer构造了生成对抗网络。生成器使用分段式设计迭代地增加输入序列长度，进而提升图像分辨率。判别器接收输入图像划分的图像块序列，用于在语义上判断输入图像是否真实。

b. 引入编码器

⚪ VAE-GAN

VAE-GAN是一种用GAN训练VAE（或用VAE训练GAN）的方法。该模型包括编码器、解码器（生成器）、判别器三部分。编码器把真实图像编码成正态分布$z$；解码器从$z$中采样生成重构图像；判别器区分真实图像和重构图像。

⚪ Bidirectional GAN (BiGAN)

BiGAN既可以将隐空间的噪声分布映射到任意复杂的数据分布，又可以将数据映射回隐空间，以此学习有价值的特征表示。该模型包括编码器、解码器（生成器）、判别器三部分。编码器把真实图像$x$编码成$z$；生成器把$z$解码成重构图像；判别器区分图像$x$和编码$z$是编码器还是解码器提供的。

⚪ VQGAN

VQGAN的生成器采用VQ-VAE模型，对图像块进行编码，学习隐空间中离散的编码表；判别器采用PatchGAN结构，用于提高生成图像的感知质量。

c. 使用能量模型

根据前面的讨论，能量模型角度下GAN的目标函数写作：

\[\begin{aligned} D^* &\leftarrow \mathop{ \min}_{D} \Bbb{E}_{x \text{~} P_{data}(x)} [ D(x)]- \Bbb{E}_{x \text{~} P_G(x)}[D(x) ] \\ G^* &\leftarrow \mathop{ \min}_{G} -H(G(z))+\Bbb{E}_{x \text{~} P_G(x)}[D(x) ] \end{aligned}\]

其中判别器$D(x)$用于近似能量函数$U(x)$，不同方法中能量函数的实现形式不同。

若直接优化上述目标，判别器倾向于对真实样本的能量$U(x)$~$D(x) \to -\infty$，对生成样本的能量$U(x)$~$D(x) \to +\infty$，从而导致训练不稳定。因此不同方法会对能量的上下限进行不同的约束。

此外，不同方法对生成图像的熵$H(G(z))$的实现形式也不同。

⚪ Energy-based GAN (EBGAN)

判别器采用自编码器形式，能量函数为自编码器的L2重构误差：

\[U(x) = ||D(x)-x||_2 = ||Dec(Enc(x))-x||_2\]

能量的最小值是$0$，最大值设置为$m$。生成图像的熵$H(G(z))$采用判别器的编码器提取的编码特征的余弦相似度衡量：

\[\begin{aligned} D^* &\leftarrow \mathop{ \min}_{D} \Bbb{E}_{x \text{~} P_{data}(x)} [ U(x)]+ \Bbb{E}_{x \text{~} P_G(x)}[\max(0, m-U(x)) ] \\ G^* &\leftarrow \mathop{ \min}_{G} \Bbb{E}_{(x_i,x_j) \text{~} P_G(x)}[(\frac{Enc(x_i)^TEnc(x_j)}{||Enc(x_i)|| \cdot ||Enc(x_j)||})^2]+\Bbb{E}_{x \text{~} P_G(x)}[U(x) ] \end{aligned}\]

⚪ Loss-Sensitive GAN (LSGAN)

能量函数为判别器$U(x)=D(x)$。

如果生成图像与真实图像差异较大，则把生成图像的能量调整得大一些。

\[\begin{aligned} D^* \leftarrow \mathop{ \min}_{D} &\Bbb{E}_{x \text{~} P_{data}(x)} [ D(x)] \\ &+ \Bbb{E}_{(x,z) \text{~}(P_{data}(x),P_z(z))}[\max \{ 0, \Delta(x,G(z))+D(x)-D(G(z)) ] \\ G^* \leftarrow \mathop{ \min}_{G} &\Bbb{E}_{x \text{~} P_G(x)}[D(x) ] \end{aligned}\]

⚪ Boundary Equilibrium GAN (BEGAN)

判别器采用自编码器形式，能量函数为自编码器的L1重构误差：

\[U(x) = ||D(x)-x||_1 = ||Dec(Enc(x))-x||_1\]

当生成图像的能量小于$\gamma$倍真实图像的能量时，判别器才会考虑增大生成图像的能量：

\[\begin{aligned} D^* &\leftarrow \mathop{ \min}_{D} \Bbb{E}_{x \text{~} P_{data}(x)} [ U(x)]- k_t \Bbb{E}_{x \text{~} P_G(x)}[U(x) ] \\ k_{t+1} &\leftarrow k_t + \lambda (\gamma U(x)-U(G(z))) \\ G^* &\leftarrow \mathop{ \min}_{G} \Bbb{E}_{x \text{~} P_G(x)}[U(x) ] \end{aligned}\]

⚪ Margin Adaptation GAN (MAGAN)

判别器采用自编码器形式，能量函数为自编码器的L2重构误差：

\[U(x) = ||D(x)-x||_2 = ||Dec(Enc(x))-x||_2\]

能量的最小值是$0$，最大值设置为$m_t$；$m_t$随训练轮数增大而减小。

\[\begin{aligned} D^* &\leftarrow \mathop{ \min}_{D} \Bbb{E}_{x \text{~} P_{data}(x)} [ U(x)]+ \Bbb{E}_{x \text{~} P_G(x)}[\max(0, m_t-U(x)) ] \\ G^* &\leftarrow \mathop{ \min}_{G} \Bbb{E}_{x \text{~} P_G(x)}[U(x) ] \end{aligned}\]

⚪ Maximum Entropy Generator (MEG)

能量函数为判别器$U(x)=D(x)$。

对于判别器，真实样本应该落在能量函数的极小值点附近，因此引入以$0$为中心的梯度惩罚，形式上等价于WGAN-GP的目标函数。

对于生成器，生成图像的熵$H(G(z))$用互信息的下界近似(引入一个编码器$E(x)$估计互信息)。

\[\begin{aligned} D^* &\leftarrow \mathop{ \min}_{D} \Bbb{E}_{x \text{~} P_{data}(x)} [ D(x)]- \Bbb{E}_{x \text{~} P_G(x)}[D(x) ] + \lambda \Bbb{E}_{x \text{~} P_{data}(x)} [ || \nabla_x D(x) ||^2 ] \\G^*,E^* &\leftarrow \mathop{ \min}_{G,E} \Bbb{E}_{z \text{~} q(z)}[||z-E(G(z))||^2]+\Bbb{E}_{x \text{~} P_G(x)}[D(x) ] \end{aligned}\]

d. 由粗到细的生成 (Coarse-to-Fine)

⚪ Laplacian Pyramid GAN (LAPGAN)

LAPGAN通过拉普拉斯金字塔生成图像。拉普拉斯金字塔存储不同尺寸的插值图像：先通过下采样操作构造低分辨率图像，然后上采样后与上一层图像作差。在生成图像时，从噪声样本出发，使用生成器构造低分辨率图像，对其进行上采样；然后将噪声和低分辨率图像通过条件生成器构造插值图像，相加后恢复为高分辨率图像。

⚪ Stacked GAN (StackGAN)

StackGAN解决了文本到图像生成分辨率不高的问题。StackGAN堆叠了两阶段的GAN，第一阶段根据给定的文本描述，生成低分辨率的图像；第二阶段根据生成的低分辨率图像以及原始文本描述，生成具有更多细节的高分辨率图像。

⚪ Progressive Growing GAN (PGGAN)

PGGAN通过在训练时逐渐地增大生成图像的分辨率获得更高质量的生成图像。渐进式的学习过程是从低分辨率图像开始生成，通过向网络中添加新的层逐步增加生成图像的分辨率。该种方法主观上允许模型首先学习图像分布的整体结构特征(低分辨率)，然后逐步学习图像的细节部分(高分辨率)。

⚪ Single Natural Image GAN (SinGAN)

SinGAN通过使用单张图像来训练GAN，使用多个GAN结构分别学习了不同尺度下图像块的分布，并从低分辨率到高分辨率逐步生成真实图像。判别器采用PatchGAN结构，输出的每个元素对应输入图像的一个子区域，用来评估该子区域的真实性。生成器接收输入噪声和上一层的低分辨率输出图像，生成高分辨率图像。

（3）改进优化过程

⚪ Improved Techniques for Training GANs

本文提出了几点使得GAN训练更快收敛的方法：

⚪ Towards Principled Methods for Training Generative Adversarial Networks

本文提出了几点解决低维流形中分布不匹配的方法：

⚪ Wasserstein GANs Work Because They Fail (to Approximate the Wasserstein Distance)

本文提出效果比较好的WGAN在训练过程中并没有精确地近似Wasserstein距离；相反如果对Wasserstein距离做更好的近似，效果反而会变差。主要原因如下：

⚪ Two Time-Scale Update Rule (TTUR)

在设置优化函数时，应设法保证判别器的判别能力比生成器的生成能力要好。通常的做法是先更新判别器的参数多次，再更新一次生成器的参数。

TTUR是指判别器和生成器的更新次数相同，将判别器的学习率设置得比生成器的学习率更大，此时网络收敛于局部纳什均衡：

\[\begin{aligned} θ_D & \leftarrow θ_D + \alpha \nabla_{θ_D}L(D,G) \\ \theta_G & \leftarrow θ_G - \beta \nabla_{θ_G}L(D,G) \end{aligned}\]

⚪ Dirac GAN

Dirac GAN把GAN的交替优化过程建模为一个由常微分方程组ODEs表示的动力系统：

\[\begin{pmatrix} \dot{\theta}_D \\ \dot{\theta}_G \end{pmatrix}= \begin{pmatrix} \nabla_{\theta_D} L(\theta_G,\theta_D) \\ -\nabla_{\theta_G} L(\theta_G,\theta_D) \end{pmatrix}\]

Dirac GAN的出发点是考虑真实样本分布只有一个样本点（记为零向量$0$）的情况。直接用向量$\theta_G$表示生成样本（也即生成器的参数），而(激活函数前的)判别器设置为线性模型$D(x)=x \cdot \theta_D$，$\theta_D$是判别器的参数。在该极简假设下，分析生成分布能否收敛到真实分布，即$\theta_G$能否最终收敛到$0$。

⚪ Variational Discriminator Bottleneck (VDB)

为防止判别器的表现能力远超生成器，变分判别瓶颈 (VDB)向判别器中引入信息瓶颈。把判别器进一步拆分成编码网络和判别网络，编码网络把$x$编码为一个隐变量$z$，判别网络把隐变量$z$预测为真假标签$y$。

VDB希望能尽可能地减少隐变量$z$包含的信息量，在实现时为损失函数引入互信息$I(x,z)$的变分上界。此时判别器的损失函数表示为：

\[\begin{aligned}\mathop{ \min}_{D,E} \mathop{ \max}_{\beta \geq 0} & \Bbb{E}_{x \text{~} P_{data}(x)}[ \Bbb{E}_{z \text{~} E(z|x)}[-\log D(z)]] + \Bbb{E}_{x \text{~} G(x)}[\Bbb{E}_{z \text{~} E(z|x)}[-\log(1-D(z))]] \\ & + \beta \left( \mathbb{E}_{x \text{~} P_{data}(x)} \left[ KL\left[ E(z|x) \mid\mid q(z)\right] \right] - I_c \right) \end{aligned}\]

⚪ Orthogonal GAN (O-GAN)

O-GAN通过对判别器的正交分解操作，把判别器变成一个编码器，从而让GAN同时具备生成能力和编码能力。实现过程为把判别器$D$写成复合函数\(D(x) = T(E(x)) = \text{avg}(E(x))\)，并在损失函数中引入Pearson相关系数：

\[\begin{aligned} \mathop{\max}_{E}& \Bbb{E}_{x \text{~} P_{data}(x)}[\log \text{avg}(E(x))] + \Bbb{E}_{z \text{~} P_{Z}(z)}[\log(1-\text{avg}(E(G(z))))] \\ & + \lambda \Bbb{E}_{z \text{~} P_{Z}(z)}[\rho(z,E(G(z)))] \\ \mathop{ \max}_{G}& \Bbb{E}_{z \text{~} P_{Z}(z)}[\log \text{avg}(E(G(z)))] + \lambda \Bbb{E}_{z \text{~} P_{Z}(z)}[\rho(z,E(G(z)))] \end{aligned}\]

⚪ Cascading Rejection

级联抑制(cascading rejection)方法是指在判别器中使用内积对特征向量$v$进行分类后，对特征向量$v$的垂直分量再做一次分类；并且再次分类也会导致一个新的垂直分量，从而实现迭代地分类：

⚪ Adaptive Discriminator Augmentation (ADA)

在小样本训练时，可以通过引入数据增强缓解判别器的过拟合现象。为了防止增强操作渗透到生成分布中，采用自适应判别器增强方法，即在训练的初始阶段设置增强概率$p=0$，当判别器出现过拟合现象时自适应地增大$p$。

⚪ Hubness Prior

枢纽度先验(Hubness Prior)是指在GAN的采样过程中，hub值越大的采样点对应的生成质量就越好。

hub值统计每个样本点出现在其余点的$k$邻域的次数；hub值越大，则越接近样本的密度中心，则该样本不太可能是没有经过充分训练的离群点，因此采样质量相对更高。

从\(\mathcal{N}(0,1)\)中采样$N$个样本点后，计算每个样本点的hub值，只保留hub值超过阈值$t$的样本点用来生成新的样本。

（4）其他应用

a. 条件生成 (Conditional Generation)

⚪ Conditional GAN (CGAN)

CGAN的生成器接收随机噪声$z$和随机标签$c$，生成给定标签$c$时的图像$x=G(z,c)$；判别器接收图像$x$和对应的标签$c$，判断图像$x$是否为给定标签$c$时的真实图像$D(x|c)$。 目标函数如下：

\[\begin{aligned} \mathop{ \min}_{G} \mathop{\max}_{D} \Bbb{E}_{x \text{~} P_{data}(x)}[\log D(x|c)] + \Bbb{E}_{z \text{~} P_{Z}(z)}[\log(1-D(G(z,c)))] \end{aligned}\]

⚪ Information Maximizing GAN (InfoGAN)

InfoGAN的生成器接收随机噪声$z$和条件编码$c$，生成给定条件$c$时的图像$x=G(z,c)$；判别器$D(x)$接收图像$x$，判断图像$x$是否为真实图像。与判别器共享参数的编码器预测生成图像$x$对应的条件编码$\hat{c}=E(G(c))$。损失函数额外引入条件编码的重构误差（实际上是条件编码$c$和生成图像$G(z,c)$的互信息$I(c;G(z,c))$的一个下界）：

\[\begin{aligned} \mathop{ \min}_{G,E} \mathop{\max}_{D} & \Bbb{E}_{x \text{~} P_{data}(x)}[\log D(x)] + \Bbb{E}_{z \text{~} P_{Z}(z)}[\log(1-D(G(z,c)))] \\ & +\lambda \Bbb{E}_{z \text{~} P_{Z}(z)}[||c-E(G(z,c))||^2] \end{aligned}\]

⚪ Auxiliary Classifier GAN (ACGAN)

ACGAN的生成器接收随机噪声$z$和随机标签$c$，生成给定标签$c$时的图像$G(z,c)$；判别器$D(x)$接收图像$x$，判断图像$x$是否为真实图像(二分类)以及是否属于对应的标签$c$(多分类)。目标函数如下：

\[\begin{aligned} \mathop{\max}_{D} & \Bbb{E}_{x \text{~} P_{data}(x)}[\log D(x)] + \Bbb{E}_{z \text{~} P_{Z}(z)}[\log(1-D(G(z,c)))] \\ & + \Bbb{E}_{c,x \text{~} P_{data}(x)}[\log D_c(x)]+ \Bbb{E}_{z \text{~} P_{Z}(z)}[\log D_c(G(z,c))] \\ \mathop{ \min}_{G} & \Bbb{E}_{z \text{~} P_{Z}(z)}[\log(D(G(z,c))] - \Bbb{E}_{z \text{~} P_{Z}(z)}[\log D_c(G(z,c))] \end{aligned}\]

⚪ Projection Discriminator

投影判别器是一种为条件生成设计的判别器结构，输入数据首先经过网络$\phi$提取特征，然后把特征分成两路：一路与编码后的类别标签$y$做点乘；另一路通过网络$\psi$映射成向量。最后两路相加作为判别器最终的输出。

\[D(x,y=c) = v_c^T\phi(x) + \psi(\phi(x))\]

b. 图像到图像翻译 (Image-to-Image Translation)

图像到图像翻译(Image-to-Image Translation)旨在学习一个映射使得图像可以从源图像域(source domain)变换到目标图像域(target domain)，同时保留图像内容(context)。

根据是否提供了一对一的学习样本对，将图像到图像翻译任务划分为有配对数据(paired data)和无配对数据(unpaired data)两种情况。

c. 超分辨率 (Super Resolution)

⚪ Super Resolution GAN (SRGAN)

SRGAN通过生成对抗网络进行图像超分辨率任务。除对抗损失外，还利用VGGNet的网络特征构造内容损失函数(content loss)。

⚪ Enhanced Super Resolution GAN (ESRGAN)

ESRGAN在SRGAN的基础上进行改进。对于网络结构，引入没有批量归一化的残差密集块作为基本单元；对于对抗损失，采用相对平均判别器的思想，让判别器预测相对真实概率；对于感知损失，采用激活前的特征来构造损失。

d. 图像修补 (Image Completion / Inpainting)

⚪ Context Encoder

上下文编码器能够根据周围像素生成任意图像区域，采用一种编码器-解码器结构，编码器接收masked输入图像，提取图像特征；解码器将图像特征解码为缺失的图像区域。

⚪ Context-Conditional GAN (CCGAN)

上下文条件GAN结合了Context Encoder和ACGAN。生成器采用一种自编码器结构，接收masked输入图像$x$，生成图像修补的结果；判别器接收图像$x$和图像标签$y$，判断图像$x$是否为真实图像(二分类)以及是否属于对应的标签$y$(多分类)。

⚪ Spatially-Adaptive Denormalization (SPADE)

SPADE能够将语义分割mask图像转换为真实图像，它通过空间自适应地学习和转换输入语义mask图像的信息。SPADE生成器将随机噪声作为输入，通过带有条件归一化SPADE层的残差块生成图像。由于每个残差块包含上采样层，因此对语义mask进行下采样以匹配空间分辨率。通过多尺度判别器构造对抗损失。

e. 机器学习应用

⚪ Semi-Supervised GAN

Semi-Supervised GAN使用GAN进行半监督学习。将原有的监督学习任务融合到GAN的判别器中，判别器同时实现数据真伪的判断和数据的分类；由生成器生成数据的标签是未知的，在原有类别的基础上多加一类作为生成数据的类别标签。

\[\begin{aligned} \mathop{ \min}_{G} \mathop{\max}_{D} & \Bbb{E}_{x \text{~} P_{data}(x)}[\log D_r(x) + D_c(\hat{y}=y |x)] \\ & + \Bbb{E}_{z \text{~} P(z)} [\log(1-D_r(G(z)))+D_c(\hat{y}=y' |G(z))] \end{aligned}\]

⚪ Anomaly Detection GAN (AnoGAN)

AnoGAN使用GAN进行图像异常检测。首先使用预处理后的正常图像训练一个常规的GAN，使其能够从隐空间中采样得到正常图像；在检测新图像时，先在隐空间中找到与该新图像匹配度最高的隐变量，将其通过GAN的生成器获得生成图像，通过对比新图像与其对应的生成图像之间的差异判断其是否为异常图像。

⚪ Clustering GAN (ClusterGAN)

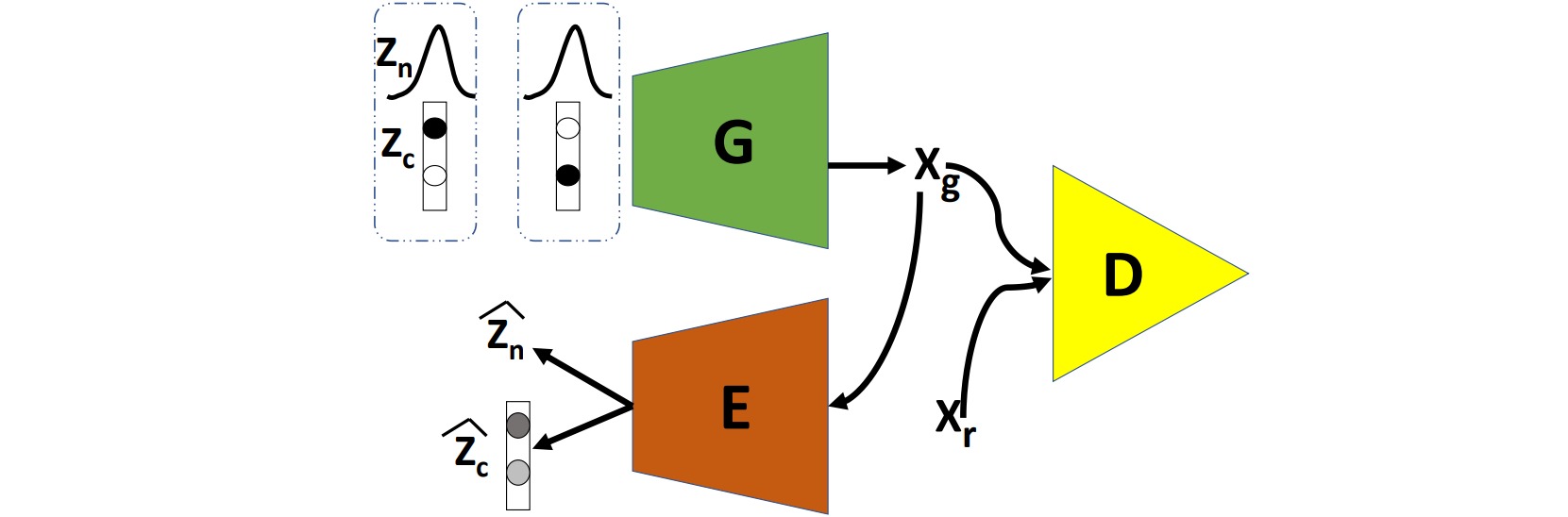
ClusterGAN通过从一个one-hot编码变量和连续隐变量的混合分布中对隐变量进行采样，实现在隐空间的聚类。网络由生成器、判别器和编码器构成。生成器$G$从一个离散分布$z_c$和连续分布$z_n$共同组成的分布中采样生成图像$x_g$；判别器$D$用于区分生成图像$x_g$和真实图像$x_r$；编码器把生成图像$x_g$编码为重构的离散编码$\hat{z}_c$和连续编码$\hat{z}_n$。

⚪ 参考文献