使用Dirac GAN分析GAN的收敛性态.
GAN的学习过程为交替优化以下目标函数:
\[\begin{aligned} \mathop{ \min}_{\theta_G} \mathop{\max}_{\theta_D} L(\theta_G,\theta_D) & = \Bbb{E}_{x \text{~} P_{data}(x)}[\log D(x;\theta_D)] + \Bbb{E}_{z \text{~} P_{Z}(z)}[\log(1-D(G(z;\theta_G);\theta_D))] \end{aligned}\]若学习算法采用梯度下降算法,则上式对应一个由常微分方程组ODEs表示的动力系统:
\[\begin{pmatrix} \dot{\theta}_D \\ \dot{\theta}_G \end{pmatrix}= \begin{pmatrix} \nabla_{\theta_D} L(\theta_G,\theta_D) \\ -\nabla_{\theta_G} L(\theta_G,\theta_D) \end{pmatrix}\]本文作者提出了Dirac GAN,用于快速地对GAN的性态进行分析:
- 收敛性态:系统的理论均衡点是否存在;令上式右端为$0$得$P_{data}(x)=P_{G}(x)$,因此GAN的均衡点通常存在。
- 局部渐近收敛性态:从任意一个初值(模型初始化)出发,经过迭代后最终能否到达理论均衡点;可以在在均衡点附近做线性展开分析。
Dirac GAN的出发点是考虑真实样本分布只有一个样本点(记为零向量$0$)的情况下,分析GAN模型的表现。
此时直接用向量$\theta_G$表示生成样本(也即生成器的参数),而(激活函数前的)判别器设置为线性模型$D(x)=x \cdot \theta_D$,$\theta_D$是判别器的参数。
Dirac GAN在该极简假设下,分析生成分布能否收敛到真实分布,即$\theta_G$能否最终收敛到$0$。
⚪ 分析non-saturating GAN
non-saturating GAN是GAN的标准形式,其目标函数如下:
\[\begin{aligned} & \mathop{ \max}_{D} \Bbb{E}_{x \text{~} P_{data}(x)}[\log D(x)] + \Bbb{E}_{z \text{~} P_z}[\log(1-D(G(z)))] \\ & \mathop{ \max}_{G} \Bbb{E}_{z \text{~} P_z}[\log D(G(z))] \end{aligned}\]在Dirac GAN假设下,目标函数简化为:
\[\begin{aligned} & \mathop{ \max}_{\theta_D} \log(1-\sigma(\theta_G \cdot \theta_D)) \\ & \mathop{ \max}_{\theta_G} \log \sigma(\theta_G \cdot \theta_D) \end{aligned}\]其中判别器的激活函数采用Sigmoid函数。上式对应的动力系统为:
\[\begin{pmatrix} \dot{\theta}_D \\ \dot{\theta}_G \end{pmatrix}= \begin{pmatrix} \nabla_{\theta_D} \log(1-\sigma(\theta_G \cdot \theta_D)) \\ \nabla_{\theta_G} \log \sigma(\theta_G \cdot \theta_D) \end{pmatrix}= \begin{pmatrix} -\sigma(\theta_G \cdot \theta_D) \cdot \theta_G \\ (1-\sigma(\theta_G \cdot \theta_D)) \cdot \theta_D \end{pmatrix}\]令上式为$0$,可得到该动力系统的均衡点为$\theta_G = \theta_D=0$下面讨论从一个初始点出发,最终能否收敛到均衡点。
假设系统已经在均衡点附近,即$\theta_G ≈ \theta_D≈0$,近似地作线性展开:
\[\begin{pmatrix} \dot{\theta}_D \\ \dot{\theta}_G \end{pmatrix}= \begin{pmatrix} -\sigma(\theta_G \cdot \theta_D) \cdot \theta_G \\ (1-\sigma(\theta_G \cdot \theta_D)) \cdot \theta_D \end{pmatrix} ≈ \begin{pmatrix} -\theta_G /2 \\ \theta_D /2 \end{pmatrix}\]因此有:
\[\ddot{\theta}_G≈-\theta_G /4\]上述常微分方程的解是周期解,并不能满足$\theta_G \to 0$。因此对于non-saturating GAN,即使模型已经相当接近均衡点,但它始终不会收敛到均衡点,而是在均衡点附近振荡。
事实上上述结果可以推广到任意以f散度为目标函数的GAN模型中,这类模型会慢慢地收敛到均衡点附近,但最终在均衡点附近振荡,无法完全收敛到均衡点。
⚪ 分析WGAN
WGAN的目标函数如下:
\[\begin{aligned} \mathop{ \min}_{G} \mathop{ \max}_{D,||D||_L \leq 1} \Bbb{E}_{x \text{~} P_{data}(x)}[D(x)]-\Bbb{E}_{x \text{~} P_{G}(x)}[D(x)] \end{aligned}\]在Dirac GAN假设下,目标函数简化为:
\[\begin{aligned} \mathop{ \min}_{\theta_G} \mathop{ \max}_{\theta_D,||\theta_D||_L \leq 1} -\theta_G \cdot \theta_D \end{aligned}\]其中Lipschitz约束通过模长归一化实现:
\[\begin{aligned} \mathop{ \min}_{\theta_G} \mathop{ \max}_{\theta_D} \frac{-\theta_G \cdot \theta_D}{||\theta_D||} \end{aligned}\]上式对应的动力系统为:
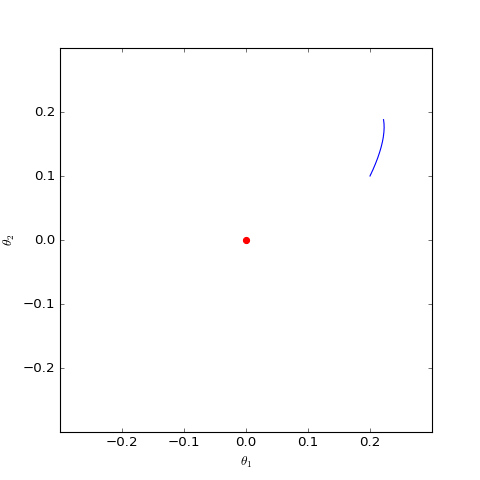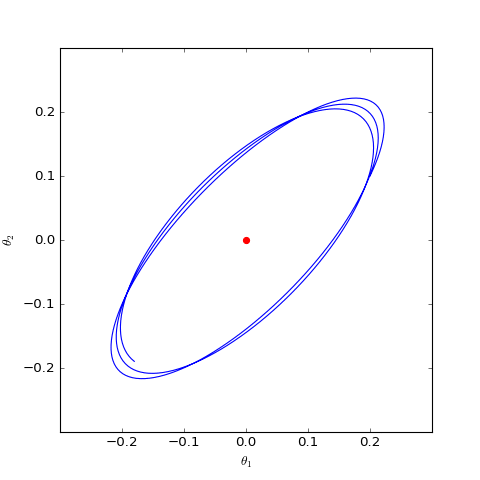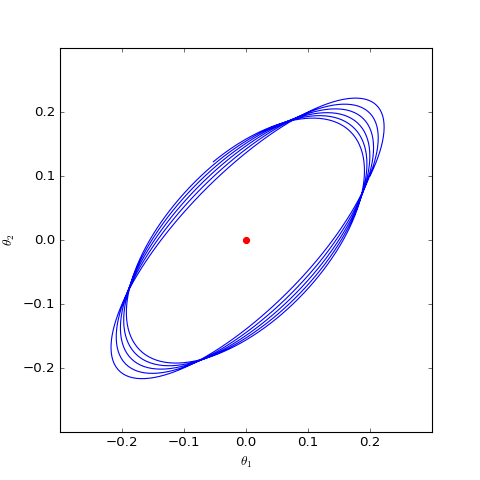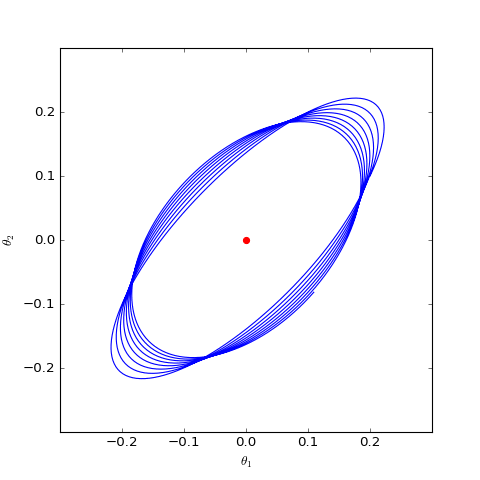
\[\begin{pmatrix} \dot{\theta}_D \\ \dot{\theta}_G \end{pmatrix}= \begin{pmatrix} \nabla_{\theta_D} \frac{-\theta_G \cdot \theta_D}{||\theta_D||} \\ -\nabla_{\theta_G}\frac{-\theta_G \cdot \theta_D}{||\theta_D||} \end{pmatrix}= \begin{pmatrix} -\theta_G/ ||\theta_D|| + (\theta_G \cdot \theta_D) \cdot \theta_D / ||\theta_D||^3 \\ \theta_D / ||\theta_D|| \end{pmatrix}\]通过数值求解,可以得到$\theta_G$在均衡点附近的优化轨迹(二维情形):
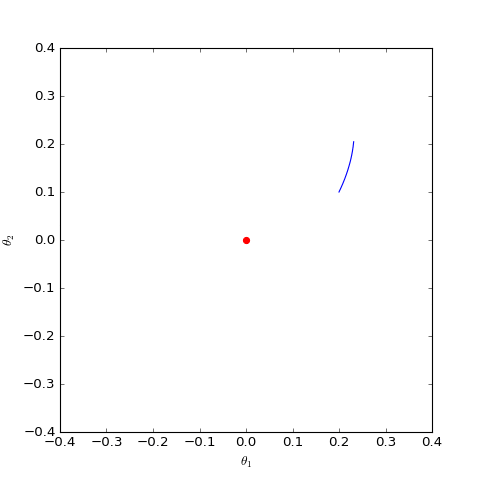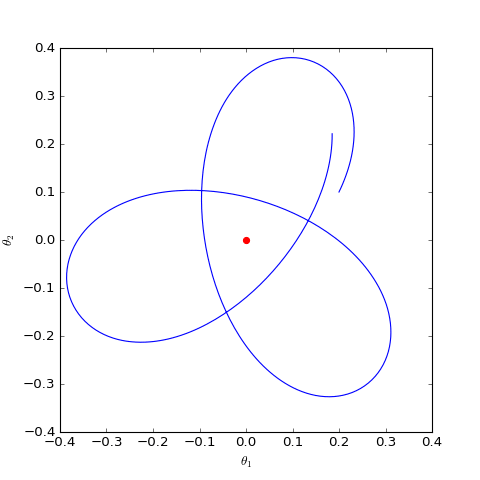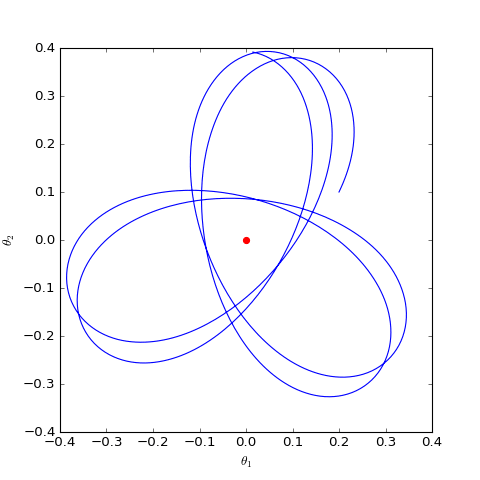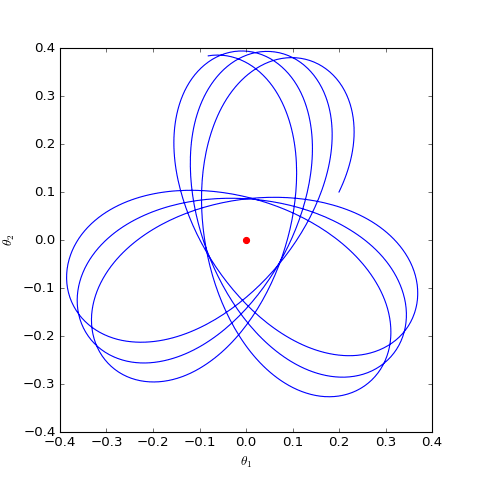
结果表明WGAN的优化过程仍然在均衡点附近振荡,并没有达到均衡点。
⚪ 分析WGAN-GP和WGAN-div
WGAN-GP通过引入梯度惩罚项来迫使判别器满足Lipschitz约束,其目标函数的形式如下:
\[\begin{aligned} \mathop{ \max}_{D} & \Bbb{E}_{x \text{~} P_{data}(x)}[D(x)]-\Bbb{E}_{x \text{~} P_{G}(x)}[D(x)] \\ & - λ \Bbb{E}_{x \text{~} \epsilon P_{data}(x) + (1-\epsilon)P_{G}(x) }[(|| \nabla_xD(x) || -c)^2] \\ \mathop{ \min}_{G}& -\Bbb{E}_{x \text{~} P_{G}(x)}[D(x)] \end{aligned}\]梯度惩罚既可以以$1$为中心,也可以以$0$为中心(对应WGAN-div)。
在Dirac GAN假设下,目标函数简化为:
\[\begin{aligned} \mathop{ \max}_{\theta_D} & -\theta_G \cdot \theta_D - λ (|| \theta_D || -c)^2 \\ \mathop{ \min}_{\theta_G}& -\theta_G \cdot \theta_D \end{aligned}\]上式对应的动力系统为:
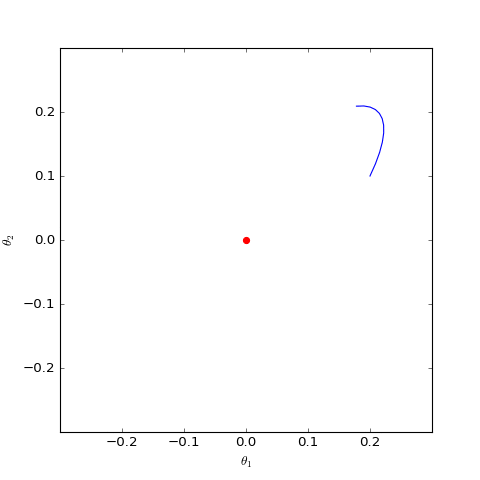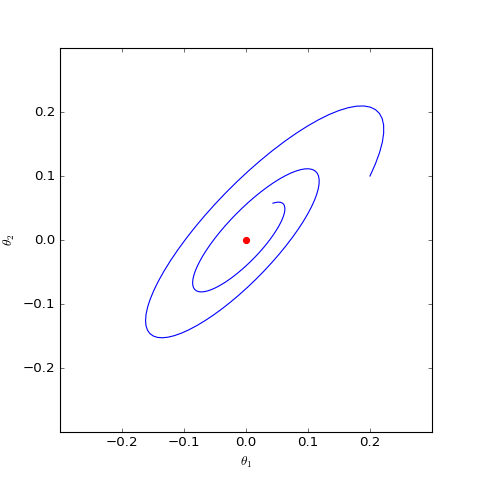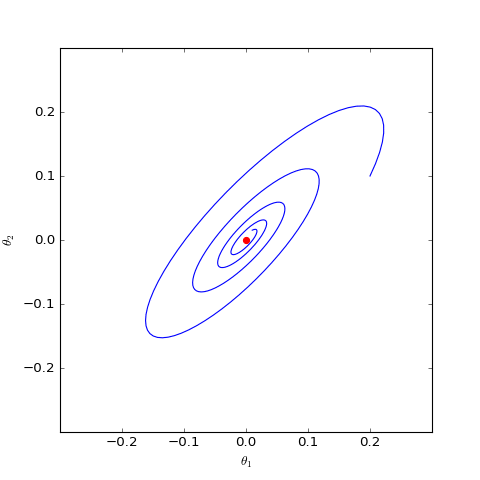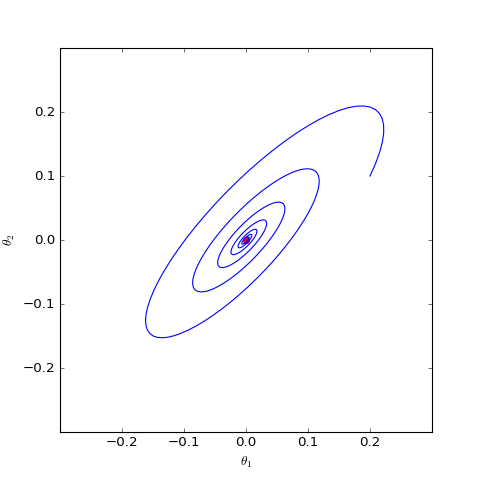
\[\begin{pmatrix} \dot{\theta}_D \\ \dot{\theta}_G \end{pmatrix}= \begin{pmatrix} \nabla_{\theta_D} (-\theta_G \cdot \theta_D - λ (|| \theta_D || -c)^2) \\ -\nabla_{\theta_G}( -\theta_G \cdot \theta_D) \end{pmatrix}= \begin{pmatrix} -\theta_G - 2λ (1 -c/|| \theta_D ||)\cdot \theta_D \\ \theta_D \end{pmatrix}\]通过数值求解,可以分别得到$c=0$和$c=1$时对应的二维情形下$\theta_G$在均衡点附近的优化轨迹:
| WGAN-div $c=0$ |
WGAN-GP $c=1$ |
|---|---|
 |
 |
结果表明,加入以$1$为中心的梯度惩罚后,模型并没有收敛到均衡点,反而只收敛到一个圆上;而加入以$0$为中心的梯度惩罚后模型收敛到均衡点。
⚪ 促进收敛的方法
根据上述分析,多数GAN模型都具有振荡性,无法渐进收敛到均衡点。下面讨论几个促进收敛的方法:
- L2正则项:向损失函数中加入判别器权重的L2正则项,会迫使判别器权重向零移动,从而打破振荡(振荡对应具有周期解的动态平衡)。
- 权重滑动平均:多数GAN模型在均衡点附近周期性振荡,振荡中心即为均衡点;因此通过平均振荡的轨迹点,可以得到近似的振荡中心。

权重滑动平均的衰减率越大,生成图像越平滑,但会丧失一些细节;衰减率越小,保留的细节越多,但也会保留额外的噪声。实验中通常设置衰减率为$0.999$。


