WGAN-div:通过Wasserstein散度构造GAN.
本文作者提出了WGAN-div,使用Wasserstein散度构造GAN的目标函数,既具有Wasserstein GAN (WGAN)的良好性质,又避免了Lipschitz约束的引入。
WGAN-div的目标函数的基本形式为:
\[\mathop{ \min}_{G} \mathop{ \max}_{D} \Bbb{E}_{x \text{~} P_{data}(x)}[D(x)]-\Bbb{E}_{x \text{~} P_{G}(x)}[D(x)] - \frac{1}{2} \Bbb{E}_{x \text{~} r(x) }[|| \nabla_xD(x) ||^2]\]其中$r(x)$是一个非常宽松的分布。
⚪ Wasserstein散度
$p(x)$和$q(x)$之间的Wasserstein散度定义为:
\[D_{W_{k,p}}[p || q] = \mathop{ \max}_{f} \int_x p(x)f(x)dx - \int_x q(x)f(x)dx - k\int_x r(x) || \nabla_xf(x) ||^p dx\]或写作采样形式:
\[D_{W_{k,p}}[p || q] = \mathop{ \max}_{f} \Bbb{E}_{x \text{~} p(x)}[f(x)] - \Bbb{E}_{x \text{~} q(x)}[f(x)] - k\Bbb{E}_{x \text{~} r(x)}[ || \nabla_xf(x) ||^p ]\]其中$f(x)$是任意函数,$r(x)$是一个样本空间跟$p(x)$和$q(x)$一样的分布,$k>0, p > 1$。
Wasserstein散度具有以下性质:
- Wasserstein散度是一个对称的散度,即$D_{W_{k,p}}[p | q]=D_{W_{k,p}}[q | p]$。
- Wasserstein散度的最优解跟Wasserstein距离具有类似的性质。
⚪ WGAN-div的目标函数
WGAN-div的训练过程为:
\[\begin{aligned} D^* &\leftarrow\mathop{ \max}_{D} \Bbb{E}_{x \text{~} P_{data}(x)}[D(x)]-\Bbb{E}_{x \text{~} P_{G}(x)}[D(x)] - k\Bbb{E}_{x \text{~} r(x)}[ || \nabla_xD(x) ||^p ] \\ G^* &\leftarrow \mathop{ \min}_{G} -\Bbb{E}_{x \text{~} P_{G}(x)}[D(x)] \end{aligned}\]⚪ WGAN-div与WGAN-GP的对比
WGAN-GP的目标函数为:
\[\mathop{ \max}_{f} \Bbb{E}_{x \text{~} p(x)}[f(x)] - \Bbb{E}_{x \text{~} q(x)}[f(x)] - k\Bbb{E}_{x \text{~} r(x)}[ (|| \nabla_xf(x) ||-n)^p ]\]取$n=1,p=2$时即为梯度惩罚项。然而上式不总是一个散度,这意味着WGAN-GP在训练判别器时并非总是在拉大两个分布的距离。
尽管WGAN-div和WGAN-GP的目标函数非常类似,但前者具有理论保证,而后者只是一种经验方案。
⚪ 实验分析
作者通过超参数搜索确定了$k=2, p =6$时效果最好:

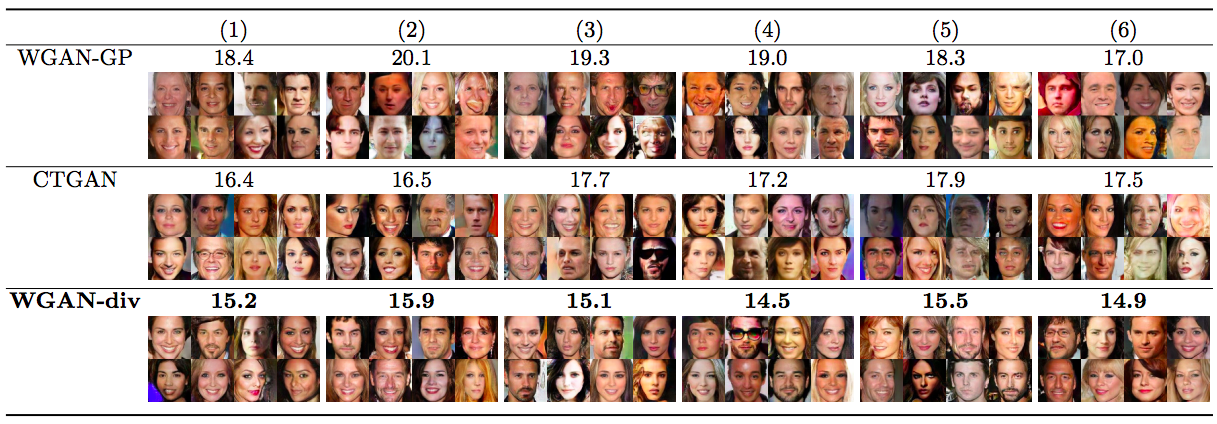
$r(x)$的选择非常宽松,作者进行了如下对比实验:
- 真假样本随机插值;
- 真样本之间随机插值,假样本之间随机插值;
- 真假样本混合后,随机选两个样本插值;
- 直接选原始的真假样本混合;
- 直接只选原始的假样本;
- 直接只选原始的真样本。
实验结果表明这几种情况下WGAN-div的表现都差不多,而WGAN-GP受到了明显的影响。
⚪ WGAN-div的pytorch实现
WGAN-div的完整pytorch实现可参考PyTorch-GAN。
下面给出损失函数计算和参数更新过程。可以使用torch.autograd.grad()方法实现网络对输入变量的求导。其中$r(x)$选择原始的真假样本混合。
k, p = 2, 6
for epoch in range(opt.n_epochs):
for i, real_imgs in enumerate(dataloader):
# 注意真实图像和生成图像都需要梯度计算
real_imgs.requires_grad_(True)
z = torch.randn(real_imgs.shape[0], opt.latent_dim)
fake_imgs = generator(z)
# 训练判别器
optimizer_D.zero_grad()
# 真实图像得分
real_validity = discriminator(real_imgs)
# 生成图像得分
fake_validity = discriminator(fake_imgs)
# 计算真实样本的梯度范数
real_grad_out = torch.ones_like(real_validity).requires_grad_(False)
real_grad = autograd.grad(
outputs=real_validity,inputs=real_imgs, grad_outputs=real_grad_out,
create_graph=True, retain_graph=True, only_inputs=True
)[0]
real_grad_norm = real_grad.view(real_grad.size(0), -1).pow(2).sum(1) ** (p/2)
# 计算生成样本的梯度范数
fake_grad_out = torch.ones_like(fake_validity).requires_grad_(False)
fake_grad = autograd.grad(
outputs=fake_validity,inputs=fake_imgs, grad_outputs=fake_grad_out,
create_graph=True, retain_graph=True, only_inputs=True
)[0]
fake_grad_norm = fake_grad.view(fake_grad.size(0), -1).pow(2).sum(1) ** (p/2)
# W散度惩罚项
w_div = torch.mean(real_grad_norm+fake_grad_norm) * k / 2
d_loss = -torch.mean(real_validity) + torch.mean(fake_validity) + w_div
d_loss.backward(retain_graph=True)
optimizer_D.step()
# 训练生成器
if i % opt.d_iter == 0:
optimizer_G.zero_grad()
g_loss = -torch.mean(discriminator(fake_imgs))
g_loss.backward()
optimizer_G.step()


