ClusterGAN:生成对抗网络的隐空间聚类.
ClusterGAN通过从一个one-hot编码变量和连续隐变量的混合分布中对隐变量进行采样,结合GAN模型和一个编码器(将数据投影到隐空间)共同训练,能够实现在隐空间的聚类。
1. 网络结构
ClusterGAN由生成器、判别器和编码器构成。
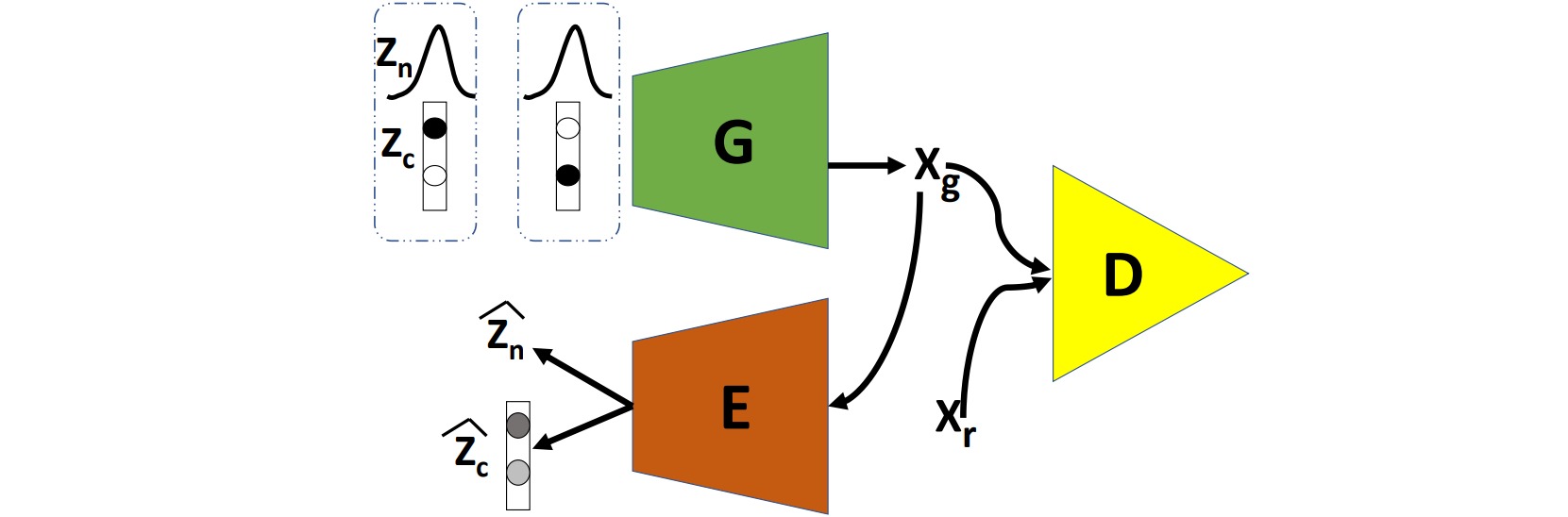
生成器$G$从一个离散分布$z_c$和连续分布$z_n$共同组成的分布中采样生成图像$x_g$;判别器$D$用于区分生成图像$x_g$和真实图像$x_r$;编码器把生成图像$x_g$编码为重构的离散编码$\hat{z}_c$和连续编码$\hat{z}_n$。
从混合分布中采样的流程如下:

def sample_z(shape=64, latent_dim=10, n_c=10, fix_class=-1, req_grad=False):
assert (fix_class == -1 or (fix_class >= 0 and fix_class < n_c) ), "Requested class %i outside bounds."%fix_class
# Sample noise as generator input, zn
zn = torch.randn((shape, latent_dim)).requires_grad_(req_grad)
######### zc, zc_idx variables with grads, and zc to one-hot vector
# Pure one-hot vector generation
zc_FT = torch.zeros((shape, n_c))
zc_idx = torch.empty(shape, dtype=torch.long)
if (fix_class == -1):
zc_idx = zc_idx.random_(n_c)
zc_FT = zc_FT.scatter_(1, zc_idx.unsqueeze(1), 1.)
else:
zc_idx[:] = fix_class
zc_FT[:, fix_class] = 1
zc = zc_FT.requires_grad_(req_grad)
# Return components of latent space variable
return zn, zc, zc_idx
训练完成后,从隐空间中采样的隐变量具有聚类特性:

2. 损失函数
ClusterGAN的目标函数可以拆分成三部分,即对抗损失、连续编码$\hat{z}_n$的L2重构损失和离散编码$\hat{z}_c$的交叉熵损失。
\[\begin{aligned} \mathop{ \min}_{G,E} \mathop{\max}_{D} & \Bbb{E}_{x \text{~} P_{data}(x)}[\log D(x)] + \Bbb{E}_{(z_n,z_c) \text{~} P(z)} [\log(1-D(G(z_n,z_c)))] \\ & + \beta_n \Bbb{E}_{(z_n,z_c) \text{~} P(z)} [||z_n-E^{n}(G(z_n,z_c))||_2^2] \\ & + \beta_c \Bbb{E}_{(z_n,z_c) \text{~} P(z)} [z_c \log E^{c}(G(z_n,z_c))] \end{aligned}\]ClusterGAN的完整pytorch实现可参考PyTorch-GAN,下面给出其损失函数的计算和参数更新过程:
# Loss function
bce_loss = torch.nn.BCELoss()
xe_loss = torch.nn.CrossEntropyLoss()
mse_loss = torch.nn.MSELoss()
# Optimizers
optimizer_G = torch.optim.Adam(
itertools.chain(E.parameters(), G.parameters()),
lr=opt.lr, betas=(opt.b1, opt.b2),
)
optimizer_D = torch.optim.Adam(D1.parameters(), lr=opt.lr, betas=(opt.b1, opt.b2))
for epoch in range(opt.n_epochs):
for i, real_imgs in enumerate(dataloader):
# Adversarial ground truths
valid = torch.ones(real_imgs.shape[0]).requires_grad_(False)
fake = torch.zeros(real_imgs.shape[0]).requires_grad_(False)
# ----------------------------------
# forward propogation
# ----------------------------------
# Sample random latent variables
zn, zc, zc_idx = sample_z(shape=real_imgs.shape[0],
latent_dim=latent_dim,
n_c=n_c)
# Generate a batch of images
gen_imgs = generator(zn, zc)
# -----------------------
# Train Discriminator
# -----------------------
optimizer_D.zero_grad()
# Discriminator output from real and generated samples
D_gen = discriminator(gen_imgs.detach())
D_real = discriminator(real_imgs)
real_loss = bce_loss(D_real, valid)
fake_loss = bce_loss(D_gen, fake)
d_loss = (real_loss + fake_loss) / 2
d_loss.backward()
optimizer_D.step()
# -------------------------------
# Train Generator and Encoder
# -------------------------------
optimizer_G.zero_grad()
enc_gen_zn, enc_gen_zc, enc_gen_zc_logits = encoder(gen_imgs)
# Calculate losses for z_n, z_c
zn_loss = mse_loss(enc_gen_zn, zn)
zc_loss = xe_loss(enc_gen_zc_logits, zc_idx)
D_gen = discriminator(gen_imgs)
gan_loss = bce_loss(D_gen, valid)
g_loss = gan_loss + betan * zn_loss + betac * zc_loss
g_loss.backward()
optimizer_G.step()


