StyleGAN3:无混叠生成对抗网络.
GAN生成的图像容易发生混叠现象,细微特征的位置不容易被控制,比如人脸已经转动,而鼻子仍然停留在原来的位置。混叠通常是由网络中的双线性插值、非线性激活等结构引入的。本文作者分析了网络不同组件实现特征的平移和旋转等变性的条件,并从StyleGAN2结构出发,从频域角度改进网络结构,实现合理的平移与旋转等变性。
1. 平移与旋转等变性分析
卷积神经网络的输入与输出均是离散变量,作者认为离散变量其实是连续变量的编码表示,连续变量与离散变量之间可以相互转化:
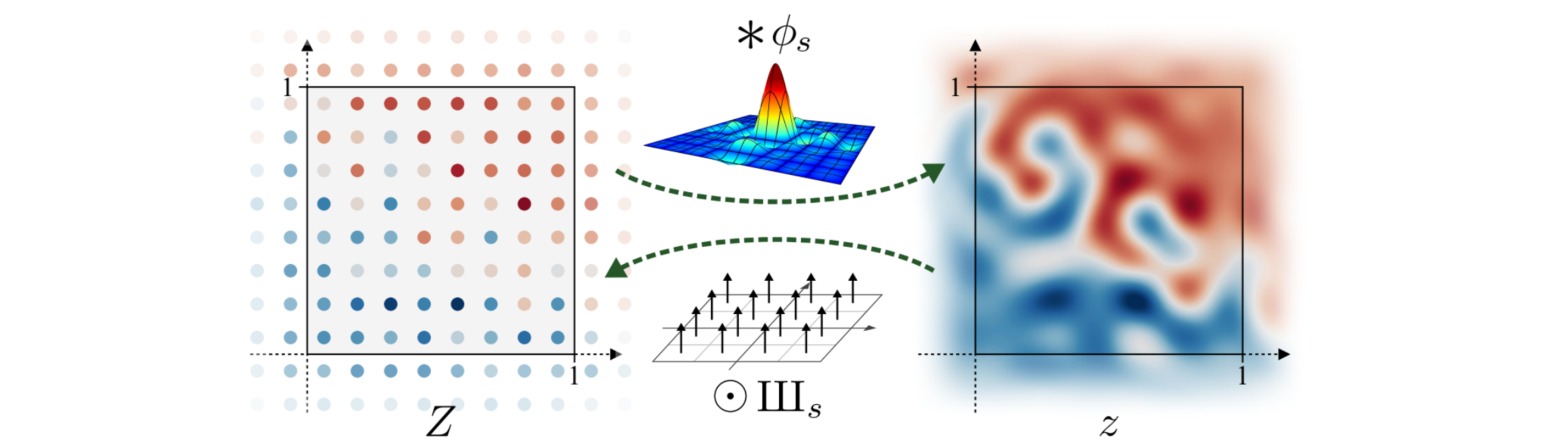
离散变量$Z$是连续变量$z$经过狄拉克梳状函数$III_s$采样得到的编码表示,而连续变量$z$则是离散变量$Z$经理想插值滤波器$\phi_s$进行卷积之后的结果。对于卷积神经网络处理离散变量的映射函数$F$和处理连续变量的映射函数$f$,具有如下关系:
\[\begin{aligned} f(z) &= \phi_{s'} * F(III_s \odot z) \\ F(Z) &= III_{s'} \odot f(\phi_s * Z) \end{aligned}\]其中$s$表示采样频率。在连续域中,假如映射$f$与某一种变换$t$存在$f \circ t = t \circ f$关系,则认为$f$对变换$t$是等变的。对于等变变换,$f$在变换后不应该导致连续变量产生混叠,即变换后的截止频率也不应该高于$s’$。
⚪ 卷积层
离散变量的卷积操作为:
\[F_{conv}(Z) = K * Z\]根据卷积的可交换性和相同的采样频率$s=s’$,连续变量的卷积操作为:
\[f_{conv}(z) = \phi_{s'} * (K *(III_s \odot z)) = K * z\]在进行平移与旋转变换时,卷积操作不会引入新的频率分量。卷积操作原本就具有平移等变性,但不具有旋转等变性,因此需要对卷积操作进行改进。
为卷积增加旋转等变性,只需要卷积核是径向对称即可。在实际使用时,直接使用简单的1×1卷积来满足这个条件。
⚪ 上采样
离散变量的上采样操作可以认为是对连续变量使用更高的截止频率$s’$进行离散化:
\[\begin{aligned} F_{up}(Z) &= III_{s'} \odot (\phi_s * Z) \end{aligned}\]这一操作理论上不会造成原始的连续变量发生变化:
\[\begin{aligned} f_{up}(z) &= \phi_{s'} * (III_{s'} \odot (\phi_s * (III_s \odot z))) = z \end{aligned}\]因此上采样操作实际上不改变连续变量,具有平移和旋转等变性。实际操作时可以将上采样过程视为先对$Z$补零,以扩大离散变量的尺寸,再对其使用离散卷积$III_{s’} \odot \phi_s$实现值的填充。
⚪ 下采样
下采样相当于对原始的连续变量进行理想低通滤波操作,剔除连续变量中的高频分量:
\[f_{down}(z) = \psi_{s'} * z\]低通滤波器是对原来的插值滤波器进行单位归一化处理得到的:$\psi_{s}=s^2 \cdot \phi_s$。
下采样后的特征图的离散表示相比于原来降低了采样率:
\[\begin{aligned} F_{down}(Z) &= III_{s'} \odot (\psi_{s'} * (\phi_s * Z)) \\ &= 1/s^2 \cdot III_{s'} \odot (\psi_{s'} * \psi_{s} * Z) \\ &\text{according to: } \psi_{s'} * \psi_{s} = \psi_{\min(s',s)} \\ &= (s'/s)^2 \cdot III_{s'} \odot (\phi_{s'} * Z) \end{aligned}\]下采样操作可以视为使用离散卷积$III_{s’} \odot \phi_{s’}$进行处理获得,因此自然满足平移等变性。将下采样的卷积操作设置为具有圆盘形频率响应的径向对称滤波器,径向对称是为了满足旋转等变性,圆盘形频率响应是为了避免二维滤波器在旋转以后难以滤除不同维度的高频分量。
⚪ 非线性激活
非线性激活函数在离散域对平移和旋转是不相容的,应用非线性激活会导致插值后的连续变量不具有等变性:
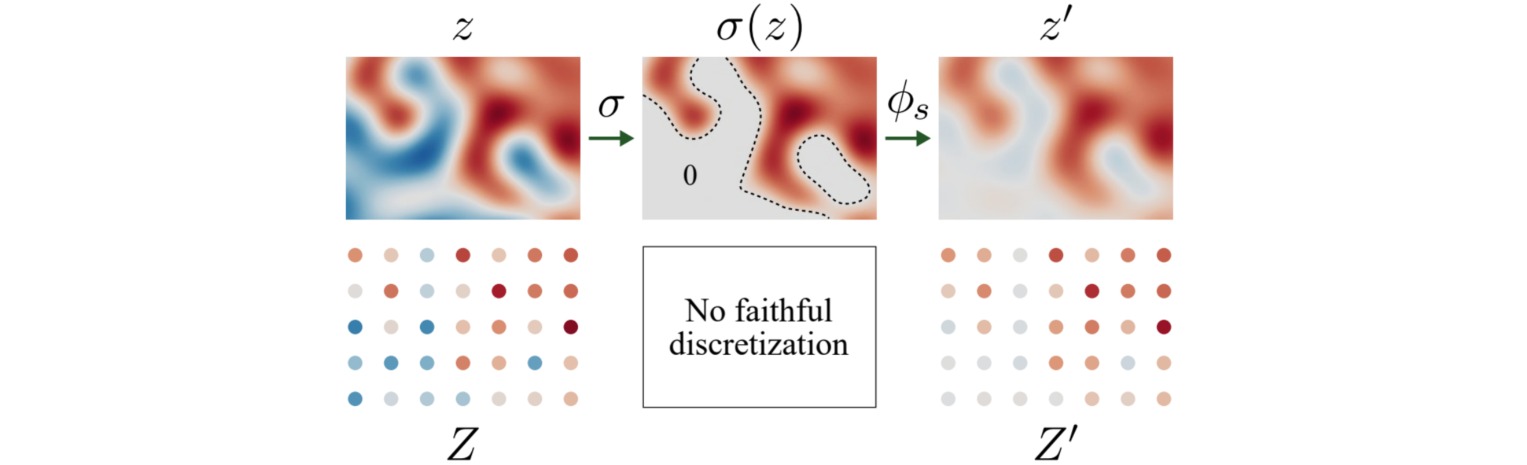
非线性激活会导致图像出现陡峭的边缘,产生新的高频分量,从而发生混叠现象。在实际应用时,通过先对离散图像进行上采样,产生一个更高分辨率的图像,再进行非线性激活,最后再下采样回原来分辨率。通过这种操作,可以在应用非线性激活之后,对图像进行下采样滤波,删除高频分量。此时可以不需要对非线性激活设计新的方法和准则,只需要满足在上采样和下采样中使用的条件即可。
2. StyleGAN3
基于不产生混叠的具有平移与旋转等变性的网络结构设计思路,作者设计了StyleGAN3网络。


⚪ 傅里叶特征 Fourier features
StyleGAN3把生成器的常量输入替换成傅里叶特征,傅里叶特征是一种从圆形频带内采样并通过一定变换生成的特征,很容易施加平移和旋转操作。这一个改进点主要是为了更好地度量模型的等变性,实际上并不能改善模型的等变性。
⚪ 变换傅里叶特征 Transformed Fourier features
可以通过输入的隐编码$A$对傅里叶特征进行仿射变换,使傅里叶特征被旋转或平移。作者认为第一层的输入对于最终的图像输出至关重要,它会起着引导图像生成结果的作用,通过仿射变换可以改善平移等变性和图像生成质量。
⚪ 不添加噪声输入 No noise input
StyleGAN3删除了逐层添加微小噪声的操作。在完整实验中发现这个操作会严重损害等变性。
⚪ 简化生成器 Simplified generator
StyleGAN3减少了神经网络的深度、去除了一些正则化和归一化操作,同时对每一层的输入施加EMA操作,这些改进可以略微提升等变性。
⚪ 像素边界扩充和上采样 Boundaries and Upsampling
平移与旋转等变性的分析过程中假设输入图像是无界的,因此在实际训练时,把图像边界扩充$10$个像素点进行输入,经过映射后再将这些扩充边界裁掉,因为边界会泄露图像的位置信息。
上采样的设计准则是尽可能接近理想插值滤波器,因此把上采样用的插值滤波器替换为带Kaiser窗的Sinc滤波器,Kaiser窗的大小为$6$,即每一个输出像素点会受到$6$个输入像素点的影响。

Kaiser窗的大小可以理解为滤波器的尺寸,实验发现Sinc滤波器会导致图像质量下降;此外对滤波器尺寸进行消融研究发现,较小的滤波器尺寸会导致平移等变性变差,但是较大的滤波器尺寸又会增加训练时间。
⚪ 滤波非线性 Filtered nonlinearity
根据旋转等变性的分析,非线性激活需要进行滤波,采用上采样-非线性激活-下采样的顺序进行处理。StyleGAN3把模块之间的上采样操作与对非线性激活的上采样操作集成在一起处理,并且自定义了一个CUDA内核完成整个运算,这样做可以节省内存,而且使训练提速$10$倍,并有效提升平移等变性。
⚪ 非临界采样 Non-critical sampling
对于图像而言,高频信息可以使图像具有更丰富的纹理特征,对图像质量至关重要,但是高频信息很容易产生混叠。通常的图像处理方法使用临界采样,以实现图像质量和抗混叠的平衡。
作者认为对于GAN模型而言,在浅层的高频信息可能没有什么意义,可以剔除掉,以进一步提升抗混叠能力。因此在实际训练时,可以考虑对除执行最高分辨率生成的网络层之外的其他网络结构设计一个更低的截止频率,提升抗混叠能力。
同时作者观察到,如果只是简单地给每个网络层施加相同的截止频率,效果可能也不会非常好,因为对于更浅的层而言,其频率分量将更集中于截止频率附近。因此使用可调截止频率策略,随着层的加深,逐渐加大截止频率。这种操作最终不仅提升了平移不变性,还提升了图像质量。

⚪ 旋转等变性 Rotation equivariant
为了实现旋转等变性,主要是把卷积操作和下采样操作的卷积核设计为径向对称的。对于卷积核,直接把3×3的卷积核换成1×1的来实现,但是这样会造成网络容量下降,因此在改变卷积核的同时把每个卷积层输出的特征数目进行加倍。对于下采样操作,使用径向对称的第一类一阶贝塞尔函数作为滤波器满足下采样的条件。旋转等变性的改进没有应用于最高分辨率生成的网络层中。


