LAPGAN:使用拉普拉斯金字塔对抗网络生成高分辨率图像.
在原始GAN中,只能生成$16×16$,$32×32$这种低像素小尺寸的图片。而LAPGAN首次实现$64×64$的图像生成。
LAPGAN采用coarse-to-fine的生成思路,与其一下子生成这么大的(包含信息量这么多),不如一步步由小到大,这样每一步生成的时候,可以基于上一步的结果,而且还只需要“填充”和“补全”新图片所需要的那些信息。
1. 拉普拉斯金字塔
拉普拉斯金字塔是一种图像存储方式,它存储不同尺寸的插值图像$L_i=G_i-rescale(G_{i+1})$;即先通过高斯模糊、下采样操作等构造低分辨率图像$G_{i+1}$,然后进行上采样后与上一层的图像$G_i$作差。

相比于存储原始图像$G_0$,存储插值图像$L_0,L_1,…$和顶部的高斯图像$G_N$需要更少的内存。这是因为插值图像的数值范围小,因此可以通过更少的比特数来存储像素;而且顶层高斯图像尺寸小。
拉普拉斯金字塔是可逆的,因此可以通过顶层高斯图像和每一层的插值图像无损地恢复原始图像。因此拉普拉斯金字塔是一种无损的图像压缩方法。

2. LAPGAN
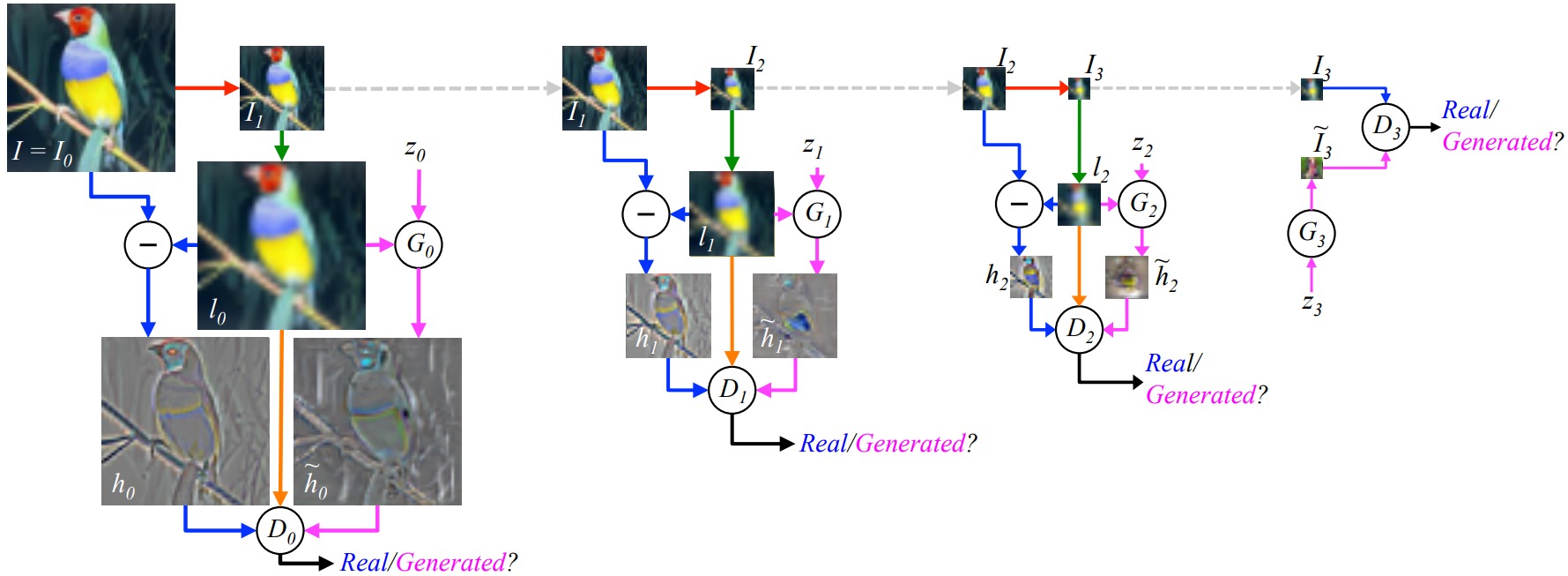
LAPGAN的工作过程如下图所示。图中给出了一个三级的图像生成过程,使用了4个生成模型对图像进行三次上采样。从一个噪声样本$z_3$开始,使用生成模型$G_3$生成尺寸为$\frac{H}{8}\times \frac{W}{8}$的图像$\tilde{I}_3$,将其经过插值上采样变为尺寸为$\frac{H}{4}\times \frac{W}{4}$的$I_2$;将输入噪声$z_2$和图像$I_2$输入生成模型$G_2$,生成图像$I_2$中缺失的细节$\tilde{h}_2$ (通常对应图像的高频部分);通过将图像$I_2$和细节$\tilde{h}_2$相加获得更清晰的图像。以此类推,最终获得完整分辨率的图像。其中首个生成模型$G_3$建模为普通GAN的生成器,其余生成模型$G_2,…,G_0$建模为条件GAN的生成器。

LAPGAN的损失函数构造过程如下图所示。由于生成模型生成细节图像,因此需要构造真实的细节图像,才能建立对抗函数。对于生成尺寸为$H\times W$的的图像$I_0$,将其通过下采样产生图像$I_1$,然后再通过插值上采样生成图像$l_0$。图像$l_0$相比于图像$I_0$缺失了图像的细节。从原始图像$I_0$中减去图像$l_0$可以得到真实的细节图像$h_0$。另一方面,将随机噪声$z_0$和图像$l_0$通过生成模型$G_0$得到生成的细节图像$\tilde{h}_0$。判别器$D_0$接收图像$l_0$和细节图像,用于区分细节图像$h_0$和$\tilde{h}_0$。
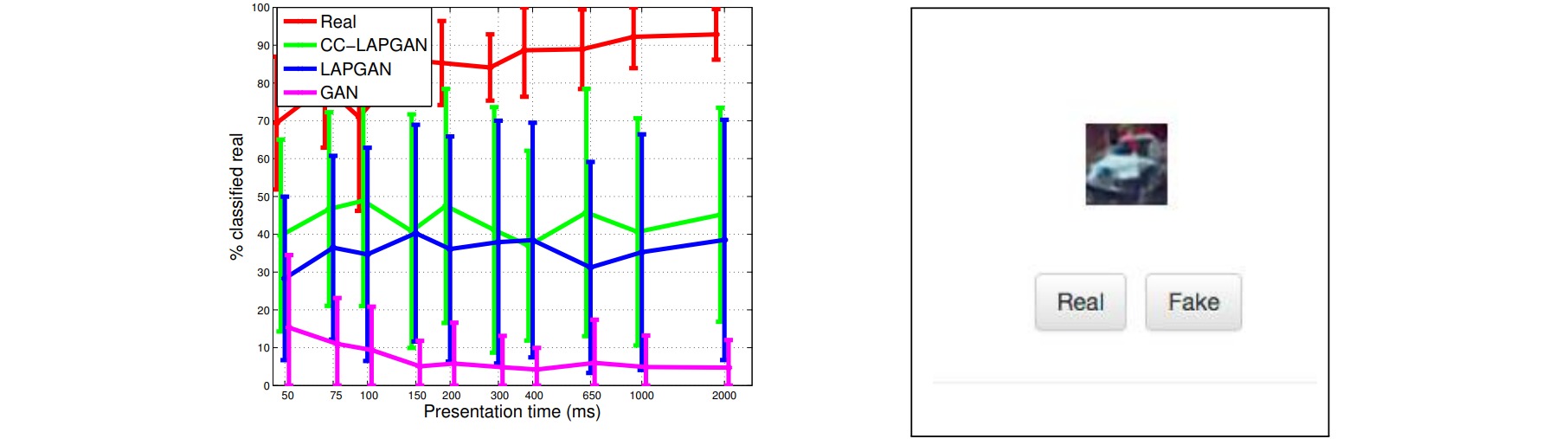
作者通过人类判别是否是自然图像来评估不同方法的性能。结果表明LAPGAN平均有$40\%$的概率生成使人类认为真实的图像。