Diffusion Model.
扩散模型 (Diffusion Model)是一类受到非平衡热力学 (non-equilibrium thermodynamics)启发的深度生成模型。这类模型首先定义前向扩散过程的马尔科夫链 (Markov Chain),向原始图像中逐渐地添加随机噪声,直至把原始图像破坏成一张完全随机的噪声图像;然后学习反向扩散过程,从噪声图像中不断减去添加噪声(由神经网络预测),最终会还原为清晰的原始图像。扩散模型也是一类隐变量模型,其隐变量通常具有较高的维度(与原始数据相同的维度)。
扩散模型的主要优点:
- 目标函数为回归损失,训练过程平稳,容易训练;
- 与像素顺序无关的逐级自回归过程,图像生成质量高。
扩散模型的主要缺点:
- 采样速度慢,单次生成需要$T$步采样;
- 没有低维空间的编码能力,无法表征和编辑隐空间。
本文目录:
- 时间离散型扩散模型的基本原理
- 时间连续型扩散模型的基本原理
- 条件扩散模型
- 生成扩散模型的优化
1. 时间离散型扩散模型的基本原理
本节介绍时间离散型扩散模型的基本原理,主要思路如下:
- 定义前向扩散过程:\(q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)\)
- 解析地推导:\(q\left(\mathbf{x}_t \mid \mathbf{x}_{0}\right)\)
- 解析地推导:\(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t,\mathbf{x}_{0}\right)\)
- 近似反向扩散过程:\(p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)\)

(1)前向扩散过程 forward diffusion process
给定从真实数据分布$q(\mathbf{x})$中采样的数据点$\mathbf{x}_0 \sim q(\mathbf{x})$,前向扩散过程定义为逐渐向样本中添加高斯噪声$\boldsymbol{\epsilon}$(共计$T$步),从而产生一系列噪声样本$\mathbf{x}_1,…,\mathbf{x}_T$。噪声的添加程度是由一系列前向方差(forward variances)系数\(\{\beta_t\in (0,1)\}_{t=1}^T\)控制的。
\[\begin{aligned} \mathbf{x}_t =\sqrt{1-\beta_t}& \mathbf{x}_{t-1}+\sqrt{\beta_t} \boldsymbol{\epsilon}_{t-1}, \boldsymbol{\epsilon}_{t-1} \sim \mathcal{N}(\mathbf{0},\mathbf{I}) \\ q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)&=\mathcal{N}\left(\mathbf{x}_t ; \sqrt{1-\beta_t} \mathbf{x}_{t-1}, \beta_t \mathbf{I}\right) \\ q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)&=\prod_{t=1}^T q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right) \end{aligned}\]在前向扩散过程中,数据样本$\mathbf{x}_0$逐渐丢失其具有判别性的特征,破坏程度由$\beta_t$控制。使用重参数化技巧,可以采样任意时刻$t$对应的噪声样本$\mathbf{x}_t$。若记$\alpha_t = 1- \beta_t$,则有:
\[\begin{array}{rlr} \mathbf{x}_t & =\sqrt{\alpha_t} \mathbf{x}_{t-1}+\sqrt{1-\alpha_t} \boldsymbol{\epsilon}_{t-1} \quad ; \text { where } \boldsymbol{\epsilon}_{t-1}, \boldsymbol{\epsilon}_{t-2}, \cdots \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \\ & =\sqrt{\alpha_t \alpha_{t-1}} \mathbf{x}_{t-2}+\sqrt{\alpha_t(1-\alpha_{t-1})} \boldsymbol{\epsilon}_{t-2}+\sqrt{1-\alpha_t} \boldsymbol{\epsilon}_{t-1} \\ & \left( \text { Note that } \mathcal{N}(\mathbf{0}, \alpha_t(1-\alpha_{t-1})) + \mathcal{N}(\mathbf{0}, 1-\alpha_{t}) = \mathcal{N}(\mathbf{0}, 1-\alpha_t\alpha_{t-1}) \right)\\ & =\sqrt{\alpha_t \alpha_{t-1}} \mathbf{x}_{t-2}+\sqrt{1-\alpha_t \alpha_{t-1}} \overline{\boldsymbol{\epsilon}}_{t-2} \\ & =\cdots \\ & =\sqrt{\prod_{i=1}^t \alpha_i} \mathbf{x}_0+\sqrt{1-\prod_{i=1}^t \alpha_i} \boldsymbol{\epsilon} \\ & =\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon} \\ q\left(\mathbf{x}_t \mid \mathbf{x}_0\right) & =\mathcal{N}\left(\mathbf{x}_t ; \sqrt{\bar{\alpha}_t} \mathbf{x}_0,\left(1-\bar{\alpha}_t\right) \mathbf{I}\right) \end{array}\]通常在前向扩散过程中会逐渐增大添加噪声的程度,即$0 \approx \beta_1<\beta_2<\cdots < \beta_T$;因此有$\bar{\alpha}_1>\cdots>\bar{\alpha}_T \approx 0$。当$T \to \infty$时,$\mathbf{x}_T$等价于一个各向同性的高斯分布。
⚪ 讨论:与随机梯度朗之万动力学的联系
朗之万动力学 (Langevin dynamics)用于对分子系统进行统计建模。结合随机梯度下降,随机梯度朗之万动力学能够从概率密度$p(\mathbf{x})$中采样,只需要使用更新过程的马尔科夫链中的梯度$\nabla_\mathbf{x} \log p(\mathbf{x})$:
\[\mathbf{x}_t=\mathbf{x}_{t-1}+\frac{\delta}{2} \nabla_{\mathbf{x}} \log p\left(\mathbf{x}_{t-1}\right)+\sqrt{\delta} \boldsymbol{\epsilon}_t, \quad \text { where } \boldsymbol{\epsilon}_t \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\]其中$\delta$是更新步长。当$T \to \infty, \epsilon \to 0$,$\mathbf{x}_T$等价于真实概率密度$p(\mathbf{x})$。与标准SGD相比,随机梯度朗之万动力学在参数更新中加入高斯噪声,以避免其崩溃到局部极小值。
(2)反向扩散过程 reverse diffusion process
如果能够求得前向扩散过程\(q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)\)的逆过程\(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)\),则能够从高斯噪声输入\(\mathbf{x}_T \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\)出发构造真实样本。注意到当$\beta_t$足够小时,\(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)\)也近似服从高斯分布。然而直接估计\(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)\)是相当困难的,我们在给定数据集的基础上通过神经网络学习条件概率\(p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)\):
\[\begin{aligned} p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)&=\mathcal{N}\left(\mathbf{x}_{t-1} ; \boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right), \boldsymbol{\Sigma}_\theta\left(\mathbf{x}_t, t\right)\right) \\ p_\theta\left(\mathbf{x}_{0: T}\right)&=p\left(\mathbf{x}_T\right) \prod_{t=1}^T p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right) \end{aligned}\]注意到如果额外引入条件\(\mathbf{x}_0\),则\(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t},\mathbf{x}_0\right)\)是可解的:
\[\begin{aligned} q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right) & =q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}, \mathbf{x}_0\right) \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_0\right)}{q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)} \\ & \propto \exp \left(-\frac{1}{2}\left(\frac{\left(\mathbf{x}_t-\sqrt{\alpha_t} \mathbf{x}_{t-1}\right)^2}{\beta_t}+\frac{\left(\mathbf{x}_{t-1}-\sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0\right)^2}{1-\bar{\alpha}_{t-1}}-\frac{\left(\mathbf{x}_t-\sqrt{\bar{\alpha}_t} \mathbf{x}_0\right)^2}{1-\bar{\alpha}_t}\right)\right) \\ & =\exp \left(-\frac{1}{2}\left(\frac{\mathbf{x}_t^2-2 \sqrt{\alpha_t} \mathbf{x}_t \mathbf{x}_{t-1}+\alpha_t \mathbf{x}_{t-1}^2}{\beta_t}+\frac{\mathbf{x}_{t-1}^2-2 \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0 \mathbf{x}_{t-1}+\bar{\alpha}_{t-1} \mathbf{x}_0^2}{1-\bar{\alpha}_{t-1}}-\frac{\left(\mathbf{x}_t-\sqrt{\bar{\alpha}_t} \mathbf{x}_0\right)^2}{1-\bar{\alpha}_t}\right)\right) \\ & =\exp \left(-\frac{1}{2}\left(\left(\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar{\alpha}_{t-1}}\right) \mathbf{x}_{t-1}^2-\left(\frac{2 \sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t+\frac{2 \sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}} \mathbf{x}_0\right) \mathbf{x}_{t-1}+C\left(\mathbf{x}_t, \mathbf{x}_0\right)\right)\right) \end{aligned}\]其中\(C\left(\mathbf{x}_t, \mathbf{x}_0\right)\)是与\(\mathbf{x}_{t-1}\)无关的项。因此\(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t},\mathbf{x}_0\right)\)也服从高斯分布:
\[\begin{aligned} q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right) & =\mathcal{N}\left(\mathbf{x}_{t-1} ; \tilde{\boldsymbol{\mu}}\left(\mathbf{x}_t, \mathbf{x}_0\right), \tilde{\beta}_t \mathbf{I}\right) \\ \tilde{\beta}_t & =1 /\left(\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar{\alpha}_{t-1}}\right)=1 /\left(\frac{\alpha_t-\bar{\alpha}_t+\beta_t}{\beta_t\left(1-\bar{\alpha}_{t-1}\right)}\right)=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \cdot \beta_t \\ \tilde{\boldsymbol{\mu}}_t\left(\mathbf{x}_t, \mathbf{x}_0\right) & =\left(\frac{\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}} \mathbf{x}_0\right) /\left(\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar{\alpha}_{t-1}}\right) \\ & =\left(\frac{\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}} \mathbf{x}_0\right) \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \cdot \beta_t \\ & =\frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_t} \mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t} \mathbf{x}_0 \end{aligned}\]注意到$\mathbf{x}_t=\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}$,因此把$\mathbf{x}_0=(\mathbf{x}_t-\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon})/\sqrt{\bar{\alpha}_t}$代入$\tilde{\boldsymbol{\mu}}_t$可得:
\[\begin{aligned} \tilde{\boldsymbol{\mu}}_t & =\frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_t} \mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t} \frac{1}{\sqrt{\bar{\alpha}_t}}\left(\mathbf{x}_t-\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}_t\right) \\ & =\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \epsilon_t\right) \end{aligned}\]⚪ 理解扩散模型的反向过程
扩散模型的反向过程是通过多步迭代来逐渐生成逼真的数据,其关键是设计概率分布\(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)\)。一般地,有:
\[q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right) = \int q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_0,\mathbf{x}_t\right)q\left(\mathbf{x}_0 \mid \mathbf{x}_t\right) d\mathbf{x}_0\]对\(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)\)的基本要求也是便于采样,落脚到\(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_0,\mathbf{x}_t\right)\)和\(q\left(\mathbf{x}_0 \mid \mathbf{x}_t\right)\)便于采样。这样一来,就可以通过下述流程完成\(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)\)的采样:
\[\hat{\mathbf{x}}_0 \sim q\left(\mathbf{x}_0 \mid \mathbf{x}_t\right), \quad \mathbf{x}_{t-1} \sim q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_0=\hat{\mathbf{x}}_0,\mathbf{x}_t\right)\]根据该分解过程,扩散模型每一步的采样\(\mathbf{x}_t \to \mathbf{x}_{t-1}\)实际上包含了两个子步骤:
- 预估:由\(q\left(\mathbf{x}_0 \mid \mathbf{x}_t\right)\)对\(\mathbf{x}_0\)做一个简单的估计;
- 修正:由\(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_0,\mathbf{x}_t\right)\)根据估计结果,将估值进行一定程度的修正。
扩散模型的反向过程就是一个反复的“预估-修正”过程,将原本难以一步到位的生成\(\mathbf{x}_t \to \mathbf{x}_0\)分解成逐步推进的过程,并且每一步都进行了数值修正。
(3)目标函数
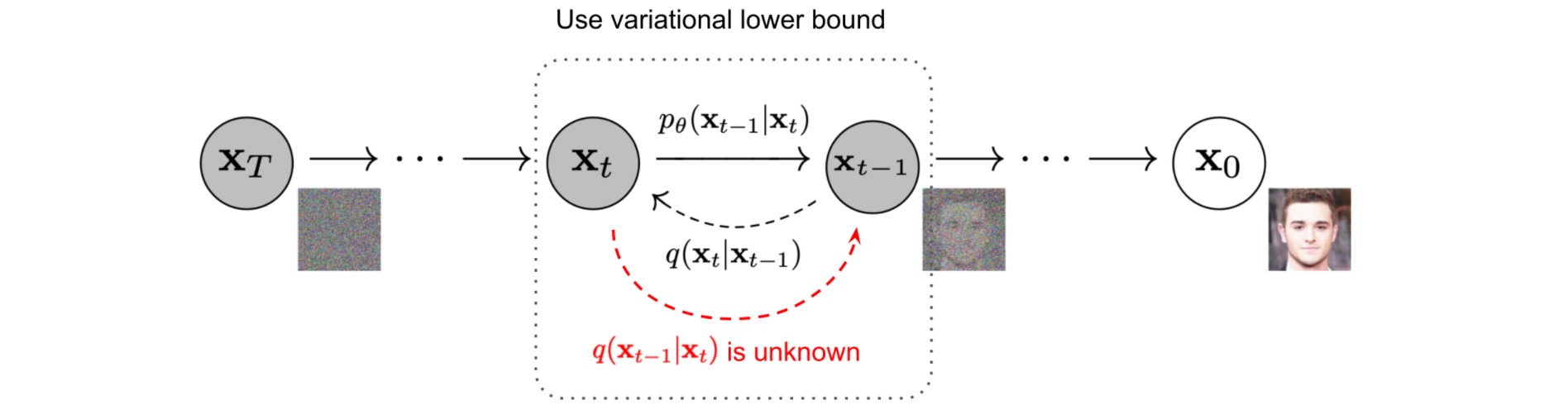
扩散模型的目标函数为最小化\(p_\theta\left(\mathbf{x}_{0}\right)\)的负对数似然\(\log p_\theta\left(\mathbf{x}_0\right)\):
\[\begin{aligned} -\log p_\theta\left(\mathbf{x}_0\right) & \leq-\log p_\theta\left(\mathbf{x}_0\right)+D_{\mathrm{KL}}\left(q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right) \| p_\theta\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)\right) \\ & =-\log p_\theta\left(\mathbf{x}_0\right)+\mathbb{E}_{\mathbf{x}_{1: T} \sim q\left(\mathbf{x}_{\left.1: T\right.} \mid \mathbf{x}_0\right)}\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{0: T}\right) / p_\theta\left(\mathbf{x}_0\right)}\right] \\ & =-\log p_\theta\left(\mathbf{x}_0\right)+\mathbb{E}_q\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{0: T}\right)}+\log p_\theta\left(\mathbf{x}_0\right)\right] \\ & =\mathbb{E}_q\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{0: T}\right)}\right] \\ \end{aligned}\]可以构造负对数似然的负变分下界 (variational lower bound):
\[L_{\mathrm{VLB}}=\mathbb{E}_{q\left(\mathbf{x}_{0: T}\right)}\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{0: T}\right)}\right] \geq-\mathbb{E}_{q\left(\mathbf{x}_0\right)} \log p_\theta\left(\mathbf{x}_0\right)\]为了把变分下界公式中的每个项转换为可计算的,可以将上述目标进一步重写为几个KL散度项和熵项的组合:
\[\begin{aligned} & L_{\mathrm{VLB}}=\mathbb{E}_{q\left(\mathbf{x}_{0: T}\right)}\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{0: T}\right)}\right] \\ & =\mathbb{E}_q\left[\log \frac{\prod_{t=1}^T q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)}{p_\theta\left(\mathbf{x}_T\right) \prod_{t=1}^T p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}\right] \\ & =\mathbb{E}_q\left[-\log p_\theta\left(\mathbf{x}_T\right)+\sum_{t=1}^T \log \frac{q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}\right] \\ & =\mathbb{E}_q\left[-\log p_\theta\left(\mathbf{x}_T\right)+\sum_{t=2}^T \log \frac{q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}+\log \frac{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)}\right] \\ & =\mathbb{E}_q\left[-\log p_\theta\left(\mathbf{x}_T\right)+\sum_{t=2}^T \log \left(\frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)} \cdot \frac{q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)}{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_0\right)}\right)+\log \frac{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)}\right] \\ & =\mathbb{E}_q\left[-\log p_\theta\left(\mathbf{x}_T\right)+\sum_{t=2}^T \log \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}+\sum_{t=2}^T \log \frac{q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)}{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_0\right)}+\log \frac{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)}\right] \\ & =\mathbb{E}_q\left[-\log p_\theta\left(\mathbf{x}_T\right)+\sum_{t=2}^T \log \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}+\log \frac{q\left(\mathbf{x}_T \mid \mathbf{x}_0\right)}{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}+\log \frac{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)}\right] \\ & =\mathbb{E}_q\left[\log \frac{q\left(\mathbf{x}_T \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_T\right)}+\sum_{t=2}^T \log \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}-\log p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)\right] \\ & =\mathbb{E}_q[\underbrace{D_{\mathrm{KL}}\left(q\left(\mathbf{x}_T \mid \mathbf{x}_0\right) \| p_\theta\left(\mathbf{x}_T\right)\right)}_{L_T}+\sum_{t=2}^T \underbrace{D_{\mathrm{KL}}\left(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right) \| p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)\right)}_{L_{t-1}}-\underbrace{\log p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)}_{L_0}] \\ \end{aligned}\]至此,扩散模型的目标函数(负变分下界)可以被分解为$T+1$项:
\[\begin{aligned} L_{\mathrm{VLB}} & =L_T+L_{T-1}+\cdots+L_0 \\ \text { where } L_T & =D_{\mathrm{KL}}\left(q\left(\mathbf{x}_T \mid \mathbf{x}_0\right) \| p_\theta\left(\mathbf{x}_T\right)\right) \\ L_t & =D_{\mathrm{KL}}\left(q\left(\mathbf{x}_t \mid \mathbf{x}_{t+1}, \mathbf{x}_0\right) \| p_\theta\left(\mathbf{x}_t \mid \mathbf{x}_{t+1}\right)\right) \text { for } 1 \leq t \leq T-1 \\ L_0 & =-\log p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right) \end{aligned}\]其中$L_T$是一个常数($q$不包含可学习参数$\theta$, $\mathbf{x}_T$是高斯噪声),在训练时可以被省略;$L_0$可以通过一个离散解码器建模;而$L_t$计算了两个高斯分布的KL散度,可以得到闭式解。
⚪ 建模$L_t$
两个正态分布\(\mathcal{N}(\mu_1,\sigma_1^2),\mathcal{N}(\mu_2,\sigma_2^2)\)的KL散度计算为$\log \frac{\sigma_2}{\sigma_1}+\frac{\sigma_1^2+(\mu_1-\mu_2)^2}{2\sigma_2^2}-\frac{1}{2}$。根据之前的讨论,我们有:
\[\begin{aligned} p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)&=\mathcal{N}\left(\mathbf{x}_{t-1} ; \boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right), \boldsymbol{\Sigma}_\theta\left(\mathbf{x}_t, t\right)\right)\\ q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right) & =\mathcal{N}\left(\mathbf{x}_{t-1} ; \frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \epsilon_t\right), \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \cdot \beta_t \mathbf{I}\right) \end{aligned}\]通过神经网络建模\(\boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right)\)和\(\boldsymbol{\Sigma}_\theta\left(\mathbf{x}_t, t\right)\),并最小化两个分布的KL散度,即可完成扩散模型的训练过程。
def normal_kl(mean1, logvar1, mean2, logvar2):
"""
KL divergence between normal distributions parameterized by mean and log-variance.
"""
return 0.5 * (-1.0 + logvar2 - logvar1 + torch.exp(logvar1 - logvar2) + ((mean1 - mean2) ** 2) * torch.exp(-logvar2))
在实践中,\(\boldsymbol{\Sigma}_\theta\left(\mathbf{x}_t, t\right)=\sigma_t^2I\)通常直接人为指定,而不视为可训练参数,以减小训练难度。而\(\boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right)\)包含两个输入\(\mathbf{x}_t, t\),即原则上对于每个不同的$t$都应构造一个不同的模型;实践中共享所有模型的参数,把$t$作为条件传入。
不妨把\(\boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right)\)进一步表示为\(\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\)的函数:
\[\boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right) = \frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right)\]则损失$L_t$可以被表示为\(\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\)的函数:
\[\begin{aligned} L_t & =\mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}}\left[\frac{1}{2\sigma_t^2}\left\|\tilde{\boldsymbol{\mu}}_t\left(\mathbf{x}_t, \mathbf{x}_0\right)-\boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right)\right\|^2\right] \\ & =\mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}}\left[\frac{1}{2\sigma_t^2}\left\|\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_t\right)-\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right)\right\|^2\right] \\ & =\mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}}\left[\frac{\left(1-\alpha_t\right)^2}{2 \alpha_t\left(1-\bar{\alpha}_t\right)\sigma_t^2}\left\|\boldsymbol{\epsilon}_t-\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right\|^2\right] \\ & =\mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}}\left[\frac{\left(1-\alpha_t\right)^2}{2 \alpha_t\left(1-\bar{\alpha}_t\right)\sigma_t^2}\left\|\boldsymbol{\epsilon}_t-\boldsymbol{\epsilon}_\theta\left(\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}_t, t\right)\right\|^2\right] \end{aligned}\]因此在扩散模型中,神经网络学习的目标是在每一步前向扩散过程中加入输入样本的噪声,并尝试在反向扩散过程中去除该噪声;因此扩散模型也被称作去噪(denoising)扩散模型。
⚪ 建模$L_0$
损失项$L_0$表示为:
\[\begin{aligned} L_0 & =-\log p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right) \end{aligned}\]其中\(\mathbf{x}_0\)表示原始图像(每个像素的取值从\(\{0,1,...,255\}\)归一化到$[-1,1]$)。因此\(p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right) = \mathcal{N}\left(\mathbf{x}_{0} ; \boldsymbol{\mu}_\theta\left(\mathbf{x}_1, 1\right), \sigma_1^2 \mathbf{I}\right)\)实现了从\(\mathbf{x}_1\)的值域到$[-1,1]$的线性映射,可以通过一个离散解码器建模(由于初始噪声很小,因此\(\mathbf{x}_1\)的值域也落在$[-1,1]$附近,将其均分为$256$份):
\[\begin{aligned} p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right) &= \prod_{i=1}^D \int_{\delta_{-}(x_0^i)}^{\delta_+(x_0^i)} \mathcal{N}\left(\mathbf{x}_{0} ; \boldsymbol{\mu}_\theta\left(\mathbf{x}_1, 1\right), \sigma_1^2 \mathbf{I}\right) \\ \delta_+(x_0^i) &= \begin{cases} \infty, & x = 1 \\ x + \frac{1}{255}, & x < 1 \end{cases} \\ \delta_-(x_0^i) &= \begin{cases}- \infty, & x = -1 \\ x - \frac{1}{255}, & x > -1 \end{cases} \end{aligned}\]则$L_0$计算为上述分布的负对数似然(NLL):
def approx_standard_normal_cdf(x):
return 0.5 * (1.0 + torch.tanh(math.sqrt(2.0 / math.pi) * (x + 0.044715 * (x ** 3))))
def discretized_gaussian_log_likelihood(x, means, log_scales, thres = 0.999):
"""
计算 -log p_{\theta}(x_0 | x_1)
"""
assert x.shape == means.shape == log_scales.shape
centered_x = x - means
inv_stdv = torch.exp(-log_scales)
plus_in = inv_stdv * (centered_x + 1. / 255.)
cdf_plus = approx_standard_normal_cdf(plus_in)
min_in = inv_stdv * (centered_x - 1. / 255.)
cdf_min = approx_standard_normal_cdf(min_in)
log_cdf_plus = math.log(cdf_plus)
log_one_minus_cdf_min = math.log(1. - cdf_min)
cdf_delta = cdf_plus - cdf_min
log_probs = torch.where(x < -thres,
log_cdf_plus,
torch.where(x > thres,
log_one_minus_cdf_min,
math.log(cdf_delta)))
return -log_probs
注意到$\beta_1 \approx 0$,即第一次前向扩散通常设置小到可以忽略的噪声,因此在实践中通常认为\(\boldsymbol{\mu}_\theta\left(\mathbf{x}_1, 1\right)\)是没有噪声的($\sigma_1 =0$);此时$L_0$与训练过程不相关,\(p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)\)是一个确定性的变换:
\[\mathbf{x}_0 = \boldsymbol{\mu}_\theta\left(\mathbf{x}_1,1\right) = \frac{1}{\sqrt{\alpha_1}}\left(\mathbf{x}_1-\sqrt{1-\alpha_1} \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_1, 1\right)\right)\](4)采样过程
通过训练,我们得到了反向扩散过程的近似条件分布:
\[\begin{aligned} p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)&=\mathcal{N}\left(\mathbf{x}_{t-1} ; \frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right), \sigma_t^2\mathbf{I}\right) \end{aligned}\]从高斯噪声中随机采样\(\mathbf{x}_T \sim \mathcal{N}(\mathbf{0}, \mathbf{I}),\mathbf{z} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\),则扩散模型的采样过程表示为:
\[\begin{aligned} \mathbf{x}_{t-1} &= \frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right)+ \sigma_t\mathbf{z}, \quad t=T,...2 \\ \mathbf{x}_{0} &= \frac{1}{\sqrt{\alpha_1}}\left(\mathbf{x}_1-\sqrt{1-\alpha_1} \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_1, 1\right)\right) \end{aligned}\](5)时间离散型扩散模型的各种变体
| 模型 | 表达式 |
|---|---|
| DDPM | 目标函数:\(\begin{aligned} \mathbb{E}_{t \sim[1, T], \mathbf{x}_0, \epsilon_t}\left[\left|\left|\boldsymbol{\epsilon}_t-\boldsymbol{\epsilon}_\theta\left(\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}_t, t\right)\right|\right|^2\right]\end{aligned}\) 采样过程: \(\begin{aligned} \mathbf{x}_{t-1} = \frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right)+ \sigma_t\mathbf{z} \end{aligned}\) 部分参数:\(\sigma_t^2=\frac{1-\overline{\alpha}_{t-1}}{1-\overline{\alpha}_{t}}\cdot \beta_t\) |
| Improved DDPM | 目标函数:\(\begin{aligned} & \mathbb{E}_{t \sim[1, T], \mathbf{x}_0, \epsilon_t}\left[\left|\left|\boldsymbol{\epsilon}_t-\boldsymbol{\epsilon}_\theta\left(\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}_t, t\right)\right|\right|^2\right] \\ & + \lambda \mathbb{E}_{t \sim[1, T], \mathbf{x}_0, \epsilon_t} \left[D_{\mathrm{KL}}\left(q\left(\mathbf{x}_t \mid \mathbf{x}_{t+1}, \mathbf{x}_0\right) || p_\theta\left(\mathbf{x}_t \mid \mathbf{x}_{t+1}\right)\right)\right] \end{aligned}\) 采样过程: 同DDPM 部分参数:\(\boldsymbol{\Sigma}_t=\exp(v \log \beta_t + (1-v) \log \tilde{\beta}_t)\) |
| DDIM | 目标函数:同DDPM 采样过程: \(\begin{aligned} \mathbf{x}_{t-1} = \frac{1}{\sqrt{\alpha_t}}\mathbf{x}_{t}+\left( \sqrt{1-\bar{\alpha}_{t-1}-\sigma_t^2}-\frac{\sqrt{1-\bar{\alpha}_t}}{\sqrt{\alpha_t}} \right) \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)+ \sigma_t \mathbf{z} \end{aligned}\) 部分参数:\(\sigma_t^2=\eta \frac{1-\overline{\alpha}_{t-1}}{1-\overline{\alpha}_{t}}\cdot \beta_t\) |
| VDM | 目标函数:\(\frac{T}{2} \mathbb{E}_{\mathbf{\epsilon}\sim \mathcal{N}(0, \mathbf{I}),i\sim U[1,T]} [(\exp(\gamma_{\eta}(i/T)-\gamma_{\eta}((i-1)/T))-1 )\left| \mathbf{\epsilon}-\hat{\mathbf{\epsilon}}_{\theta}(\mathbf{x}_t;t)\right|_2^2]\) 采样过程: \(\hat{\mathbf{x}}_{\theta}(\mathbf{x}_t;t) = \frac{\mathbf{x}_t-\sigma_t\hat{\mathbf{\epsilon}}_{\theta}(\mathbf{x}_t;t)}{\alpha_t}\) |
| Analytic-DPM | 目标函数:同DDPM 采样过程: \(\begin{aligned} \mathbf{x}_{t-1} =& \frac{1}{\sqrt{\alpha_t}}\mathbf{x}_{t}+\left( \sqrt{1-\bar{\alpha}_{t-1}-\sigma_t^2}-\frac{\sqrt{1-\bar{\alpha}_t}}{\sqrt{\alpha_t}} \right) \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right) \\& + \sqrt{\sigma_t^2 + \left( \sqrt{\bar{\alpha}_{t-1}} - \sqrt{\frac{\bar{\alpha}_{t}(1-\bar{\alpha}_{t-1}-\sigma_t^2)}{1-\bar{\alpha}_{t}}} \right)^2\hat{\sigma}_t^2}\mathbf{z} \end{aligned}\) 部分参数:\(\begin{aligned} \sigma_t^2&=\eta \frac{1-\overline{\alpha}_{t-1}}{1-\overline{\alpha}_{t}}\cdot \beta_t \\ \hat{\sigma}_t^2&= \frac{1-\bar{\alpha}_t}{\bar{\alpha}_t} \left(1-\frac{1}{d}\mathbb{E}_{\mathbf{x}_t \sim q\left(\mathbf{x}_{t}\right)} \left[ ||\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right) ||^2 \right] \right) \end{aligned}\) |
| Extended-Analytic-DPM | 目标函数:同DDPM 采样过程: \(\begin{aligned} \mathbf{x}_{t-1} =& \frac{1}{\sqrt{\alpha_t}}\mathbf{x}_{t}+\left( \sqrt{1-\bar{\alpha}_{t-1}-\sigma_t^2}-\frac{\sqrt{1-\bar{\alpha}_t}}{\sqrt{\alpha_t}} \right) \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right) \\& + \sqrt{\sigma_t^2 + \left( \sqrt{\bar{\alpha}_{t-1}} - \sqrt{\frac{\bar{\alpha}_{t}(1-\bar{\alpha}_{t-1}-\sigma_t^2)}{1-\bar{\alpha}_{t}}} \right)^2\hat{\sigma}_t^2}\mathbf{z} \end{aligned}\) 部分参数:\(\begin{aligned} \sigma_t^2&=\eta \frac{1-\overline{\alpha}_{t-1}}{1-\overline{\alpha}_{t}}\cdot \beta_t \\ \hat{\sigma}_t^2&= \frac{1-\bar{\alpha}_t}{\bar{\alpha}_t}\mathop{\arg\min}_{\mathbb{g}(\mathbf{x}_t)}\mathbb{E}_{\mathbf{x}_t ,\mathbf{x}_0 \sim q\left(\mathbf{x}_{t} \mid \mathbf{x}_0\right)q\left(\mathbf{x}_{0}\right)}\left[\left|\left| \left(\boldsymbol{\epsilon}_t-\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right) \right)^2-\mathbb{g}(\mathbf{x}_t)\right|\right|^2\right] \end{aligned}\) |
| Cold Diffusion | 目标函数:\(\begin{aligned} \mathbb{E}_{t \sim[1, T], \mathbf{x}_0}\left[\left|\left|\mathbf{x}_0 - \mathcal{G}_t(\mathcal{F}_t (\mathbf{x}_{0}))\right|\right|_1\right]\end{aligned}\) 采样过程: \(\begin{aligned} \mathbf{x}_{t-1} =& \mathbf{x}_t+\mathcal{F}_{t-1} (\mathcal{G}_t(\mathbf{x}_t)) - \mathcal{F}_t (\mathcal{G}_t(\mathbf{x}_t)) \\\mathbf{x}_{t-1} =& \mathcal{F}_{t-1} (\mathcal{G}_t(\mathbf{x}_t)) \end{aligned}\) |
2. 时间连续型扩散模型的基本原理
可以把扩散模型理解为一个在时间上连续的变换过程,并用随机微分方程(Stochastic Differential Equation,SDE)来描述。
(1)前向扩散SDE
前向扩散过程可以用SDE描述为:
\[d \mathbf{x} = \mathbf{f}_t(\mathbf{x})dt+g_t d\mathbf{w}\]其中\(\mathbf{w}\)是标准维纳过程;\(\mathbf{f}_t(\cdot )\)是一个向量函数,被称为\(\mathbf{x}(t)\)的漂移系数(drift coefficient)。\(g(\cdot )\)是一个标量函数,被称为\(\mathbf{x}(t)\)的扩散系数(diffusion coefficient)。
前向扩散SDE也可以等价地写成以下差分方程的形式:
\[\mathbf{x}_{t+\Delta t}-\mathbf{x}_t = \mathbf{f}_t(\mathbf{x}_t)\Delta t + g_t \sqrt{\Delta t} \boldsymbol{\epsilon},\boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\]或写作概率模型:
\[\begin{aligned} p(\mathbf{x}_{t+\Delta t} \mid \mathbf{x}_t) &= \mathcal{N}\left(\mathbf{x}_{t+\Delta t};\mathbf{x}_t+\mathbf{f}_t(\mathbf{x}_t)\Delta t, g_t^2 \Delta t\mathbf{I}\right) \\ & \propto \exp\left( -\frac{||\mathbf{x}_{t+\Delta t}-\mathbf{x}_t-\mathbf{f}_t(\mathbf{x}_t)\Delta t||^2}{2g_t^2 \Delta t} \right) \end{aligned}\](2)反向扩散SDE
反向扩散SDE旨在求解\(p(\mathbf{x}_{t} \mid \mathbf{x}_{t+\Delta t})\)。根据贝叶斯定理:
\[\begin{aligned} p(\mathbf{x}_{t} \mid \mathbf{x}_{t+\Delta t}) &= \frac{p(\mathbf{x}_{t+\Delta t} \mid \mathbf{x}_{t})p(\mathbf{x}_{t})}{p(\mathbf{x}_{t+\Delta t})} = p(\mathbf{x}_{t+\Delta t} \mid \mathbf{x}_{t}) \exp \left( \log p(\mathbf{x}_{t}) - \log p(\mathbf{x}_{t+\Delta t}) \right) \\ &\propto \exp\left( -\frac{||\mathbf{x}_{t+\Delta t}-\mathbf{x}_t-\mathbf{f}_t(\mathbf{x}_t)\Delta t||^2}{2g_t^2 \Delta t} + \log p(\mathbf{x}_{t}) - \log p(\mathbf{x}_{t+\Delta t})\right) \end{aligned}\]通常$\Delta t$比较小,因此有泰勒展开:
\[\log p(\mathbf{x}_{t+\Delta t}) = \log p(\mathbf{x}_{t}) + (\mathbf{x}_{t+\Delta t}-\mathbf{x}_t) \cdot \nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t) + \mathcal{O}(\Delta t)\]代入上式并配方得:
\[\begin{aligned} p(\mathbf{x}_{t} \mid \mathbf{x}_{t+\Delta t}) &\propto \exp\left( -\frac{||\mathbf{x}_{t+\Delta t}-\mathbf{x}_t-[\mathbf{f}_t(\mathbf{x}_t)-g_t^2\nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t)]\Delta t||^2}{2g_t^2 \Delta t} + \mathcal{O}(\Delta t)\right) \\ & \approx \exp\left( -\frac{||\mathbf{x}_t-\mathbf{x}_{t+\Delta t}+[\mathbf{f}_t(\mathbf{x}_t)-g_t^2\nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t)]\Delta t||^2}{2g_t^2 \Delta t}\right) \\ & \sim \mathcal{N}\left(\mathbf{x}_t;\mathbf{x}_{t+\Delta t}-[\mathbf{f}_t(\mathbf{x}_t)-g_t^2\nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t)]\Delta t, g_t^2 \Delta t\mathbf{I}\right) \end{aligned}\]上式也可写作差分方程:
\[\mathbf{x}_t-\mathbf{x}_{t+\Delta t} = -[\mathbf{f}_{t+\Delta t}(\mathbf{x}_{t+\Delta t})-g_{t+\Delta t}^2\nabla_{\mathbf{x}_{t+\Delta t}} \log p(\mathbf{x}_{t+\Delta t})]\Delta t + g_{t+\Delta t} \sqrt{\Delta t} \boldsymbol{\epsilon},\boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\]取$\Delta t \to 0$,得到反向过程对应的SDE:
\[d \mathbf{x} = [\mathbf{f}_t(\mathbf{x})-g_t^2\nabla_{\mathbf{x}} \log p_t(\mathbf{x})]dt+g_t d\mathbf{w}\](3)得分匹配
前向和反向扩散过程的SDE:
\[\begin{aligned} d \mathbf{x} &= \mathbf{f}_t(\mathbf{x})dt+g_t d\mathbf{w} \\ d \mathbf{x} &= [\mathbf{f}_t(\mathbf{x})-g_t^2\nabla_{\mathbf{x}} \log p_t(\mathbf{x})]dt+g_t d\mathbf{w} \end{aligned}\]也可以等价地写成差分形式:
\[\begin{aligned} \mathbf{x}_{t+\Delta t}-\mathbf{x}_t &= \mathbf{f}_t(\mathbf{x}_t)\Delta t + g_t \sqrt{\Delta t} \boldsymbol{\epsilon},\boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \\ \mathbf{x}_t-\mathbf{x}_{t+\Delta t} &= -[\mathbf{f}_{t+\Delta t}(\mathbf{x}_{t+\Delta t})-g_{t+\Delta t}^2\nabla_{\mathbf{x}_{t+\Delta t}} \log p(\mathbf{x}_{t+\Delta t})]\Delta t + g_{t+\Delta t} \sqrt{\Delta t} \boldsymbol{\epsilon},\boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \end{aligned}\]如果进一步知道\(\nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t)\),就可以通过反向SDE完成生成过程。
考虑到在离散型的扩散模型中,通常会为\(p(\mathbf{x}_t \mid \mathbf{x}_0)\)设计具有解析解的形式。此时\(\nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t)\)表示为:
\[\begin{aligned} p(\mathbf{x}_t) &= \mathbb{E}_{\mathbf{x}_0} \left[ p(\mathbf{x}_t \mid \mathbf{x}_0)\right] \\ \nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t) &= \frac{\mathbb{E}_{\mathbf{x}_0} \left[ \nabla_{\mathbf{x}_t} p(\mathbf{x}_t \mid \mathbf{x}_0)\right]}{ \mathbb{E}_{\mathbf{x}_0} \left[ p(\mathbf{x}_t \mid \mathbf{x}_0)\right]} \\ &= \frac{\mathbb{E}_{\mathbf{x}_0} \left[p(\mathbf{x}_t \mid \mathbf{x}_0) \nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t \mid \mathbf{x}_0)\right]}{ \mathbb{E}_{\mathbf{x}_0} \left[ p(\mathbf{x}_t \mid \mathbf{x}_0)\right]} \end{aligned}\]上式表示\(\nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t)\)计算为\(\nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t \mid \mathbf{x}_0)\)在分布\(p(\mathbf{x}_t \mid \mathbf{x}_0)\)上的加权平均。
我们希望用神经网络学一个函数\(s_θ(\mathbf{x}_t,t)\),使得它能够直接计算\(\nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t)\)。则\(s_θ(\mathbf{x}_t,t)\)应当也能表示为\(\nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t \mid \mathbf{x}_0)\)在分布\(p(\mathbf{x}_t \mid \mathbf{x}_0)\)上的加权平均,或者等价地写成如下损失:
\[\begin{aligned} & \frac{\mathbb{E}_{\mathbf{x}_0} \left[p(\mathbf{x}_t \mid \mathbf{x}_0)|| s_θ(\mathbf{x}_t,t)- \nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t \mid \mathbf{x}_0)||^2\right]}{ \mathbb{E}_{\mathbf{x}_0} \left[ p(\mathbf{x}_t \mid \mathbf{x}_0)\right]} \\ \propto & \int \mathbb{E}_{\mathbf{x}_0} \left[p(\mathbf{x}_t \mid \mathbf{x}_0)|| s_θ(\mathbf{x}_t,t)- \nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t \mid \mathbf{x}_0)||^2\right] d\mathbf{x}_t \\ = & \mathbb{E}_{\mathbf{x}_0,\mathbf{x}_t \sim p(\mathbf{x}_t \mid \mathbf{x}_0)p(\mathbf{x}_0)} \left[|| s_θ(\mathbf{x}_t,t)- \nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t \mid \mathbf{x}_0)||^2\right] \end{aligned}\]上式被称为(条件)得分匹配 (score matching)损失。
(4)连续型扩散模型的一般流程

构造连续型扩散模型的一般流程:
① 通过随机微分方程定义前向扩散过程:
\[\begin{aligned} d \mathbf{x} = \mathbf{f}_t(\mathbf{x})dt+g_t d\mathbf{w} \end{aligned}\]② 求\(p(\mathbf{x}_t \mid \mathbf{x}_0)\)的表达式;
③ 通过得分匹配损失训练\(s_θ(\mathbf{x}_t,t)\):
\[\begin{aligned} \mathbb{E}_{\mathbf{x}_0,\mathbf{x}_t \sim p(\mathbf{x}_t \mid \mathbf{x}_0)p(\mathbf{x}_0)} \left[|| s_θ(\mathbf{x}_t,t)- \nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t \mid \mathbf{x}_0)||^2\right] \end{aligned}\]④ 通过随机微分方程实现反向扩散过程:
\[\begin{aligned} d \mathbf{x} = [\mathbf{f}_t(\mathbf{x})-g_t^2s_θ(\mathbf{x}_t,t)]dt+g_t d\mathbf{w} \end{aligned}\](5)由SDE到ODE
扩散模型对应了一个随机微分方程,实际上也隐含了一个常微分方程 (ordinary differential equation, ODE)。相比于SDE,ODE用于描述确定性系统的动态行为,不涉及随机性,具有更好的数值稳定性,并且可以实现加速采样。
(6)时间连续型扩散模型的各种变体
| 模型 | 表达式 |
|---|---|
| Variance Exploding SDE | 前向扩散:\(d \mathbf{x} = \sqrt{\frac{d\bar{\beta}_t}{dt}} d\mathbf{w}\) |
| Variance Preserving SDE | 前向扩散: \(d \mathbf{x} = -\frac{\bar{\gamma}_t}{2} \mathbf{x}dt+\sqrt{\bar{\gamma}_t} d\mathbf{w}, \bar{\gamma}_t=\bar{\alpha}_t\frac{d}{dt}\left(\frac{\bar{\beta}_t}{\bar{\alpha}_t}\right)\) |
| Probability Flow ODE | 前向扩散:\(d \mathbf{x} = \left(\mathbf{f}_t(\mathbf{x}) -\frac{1}{2}g_t^2\nabla_\mathbf{x} \log p_t(\mathbf{x})\right)dt\) |
| Rectified Flow | 前向扩散:\(d\mathbf{x} = s_{\theta}(\mathbf{x},t) dt\) 目标函数:\(\mathbb{E}_{x_0\sim p_0(x_0),x_T\sim p_T(x_T)}\left[ \left| s_\theta((x_1-x_0)t+x_0,t) - (x_1-x_0) \right|^2 \right]\) |
| Poisson Flow | 前向扩散:\(\mathbf{x} = \mathbf{x}_0 + || \epsilon_x||(1+\tau)^m \mathbf{u}, \quad t= |\epsilon_t|(1+\tau)^m\) 目标函数:\(\left|\left| s_{\theta}(\mathbf{x},t)+ \text{Norm} \left(\mathbb{E}_{\mathbf{x}_0 \sim p(\mathbf{x}_0)} \left[\frac{(\mathbf{x}-\mathbf{x}_0,t)}{(\left|\left|\mathbf{x}-\mathbf{x}_0\right|\right|^2 + t^2 )^{(d+1)/2}}\right]\right) \right|\right|^2\) 反向扩散:\(\frac{d \mathbf{x}}{dt} = \frac{F_\mathbf{x}}{F_t}, s_{\theta}(\mathbf{x},t) = (F_\mathbf{x},F_t)\) |
3. 条件扩散模型
条件扩散模型是指根据给定的条件来控制生成结果,即在采样过程\(p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)\)中引入输入条件\(\mathbf{y}\),使得采样过程变为\(p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t,\mathbf{y}\right)\)。条件控制生成的方式可分为两种:事后修改(Classifier-Guidance)和事前训练(Classifier-Free)。
(1)事后修改 Classifier-Guidance
事后修改是指在已经训练好的无条件扩散模型的基础上引入一个可训练的分类器(Classifier),用分类器来调整生成过程以实现控制生成。这类模型的训练成本比较低,但是采样成本会高一些,而且难以控制生成图像的细节。
⚪ 离散形式的事后修改
为了重用训练好的模型\(p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)\),根据贝叶斯定理:
\[\begin{aligned} p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t,\mathbf{y}\right) &= \frac{p_{\theta}\left(\mathbf{x}_{t-1} , \mathbf{x}_t,\mathbf{y}\right)}{p_{\theta}\left(\mathbf{x}_t,\mathbf{y}\right)} \\ &= \frac{p_{\theta}\left(\mathbf{y} \mid \mathbf{x}_{t-1} , \mathbf{x}_t\right)p_{\theta}\left(\mathbf{x}_{t-1} , \mathbf{x}_t\right)}{p_{\theta}\left(\mathbf{y}\mid \mathbf{x}_t\right)p_{\theta}\left(\mathbf{x}_t\right)} \\ &= \frac{p_{\theta}\left(\mathbf{y} \mid \mathbf{x}_{t-1} , \mathbf{x}_t\right)p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}{p_{\theta}\left(\mathbf{y}\mid \mathbf{x}_t\right)} \\ &= \frac{p_{\theta}\left(\mathbf{y} \mid \mathbf{x}_{t-1}\right)p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}{p_{\theta}\left(\mathbf{y}\mid \mathbf{x}_t\right)} \\ &= p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right) e^{\log p_{\theta}\left(\mathbf{y} \mid \mathbf{x}_{t-1}\right) - \log p_{\theta}\left(\mathbf{y} \mid \mathbf{x}_t\right)} \end{aligned}\]为了进一步得到可采样的近似结果,在\(\mathbf{x}_{t-1}=\boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right)\)处考虑泰勒展开:
\[\begin{aligned} \log p_{\theta}\left(\mathbf{y} \mid \mathbf{x}_{t-1}\right) \approx \log p_{\theta}\left(\mathbf{y} \mid \mathbf{x}_t\right) + (\mathbf{x}_{t-1}-\boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right)) \cdot \nabla_{\mathbf{x}_t} \log p_{\theta}\left(\mathbf{y} \mid \mathbf{x}_t\right)|_{\mathbf{x}_t=\boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right)} + \mathcal{O}(\mathbf{x}_t) \end{aligned}\]并注意到反向扩散过程的建模:
\[\begin{aligned} p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)&=\mathcal{N}\left(\mathbf{x}_{t-1} ; \boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right), \sigma_t^2 \mathbf{I}\right) \\ \end{aligned}\]因此有:
\[\begin{aligned} p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t,\mathbf{y}\right) &=p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right) e^{\log p_{\theta}\left(\mathbf{y} \mid \mathbf{x}_{t-1}\right) - \log p_{\theta}\left(\mathbf{y} \mid \mathbf{x}_t\right)} \\ &\propto \exp\left(-\frac{\left\| \mathbf{x}_{t-1} -\boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right) \right\|^2}{2\sigma_t^2}+(\mathbf{x}_{t-1}-\boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right)) \cdot \nabla_{\mathbf{x}_t} \log p_{\theta}\left(\mathbf{y} \mid \mathbf{x}_t\right)|_{\mathbf{x}_t=\boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right)} + \mathcal{O}(\mathbf{x}_t) \right) \\ &\propto \exp\left(-\frac{\left\| \mathbf{x}_{t-1} -\boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right)-\sigma_t^2 \nabla_{\mathbf{x}_t} \log p_{\theta}\left(\mathbf{y} \mid \mathbf{x}_t\right)|_{\mathbf{x}_t=\boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right)}\right\|^2}{2\sigma_t^2} + \mathcal{O}(\mathbf{x}_t) \right) \\ \end{aligned}\]则\(p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t,\mathbf{y}\right)\)近似服从正态分布:
\[\begin{aligned} p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t,\mathbf{y}\right)=\mathcal{N}\left(\mathbf{x}_{t-1} ; \boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right)+\sigma_t^2 \nabla_{\mathbf{x}_t} \log p_{\theta}\left(\mathbf{y} \mid \mathbf{x}_t\right)|_{\mathbf{x}_t=\boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right)}, \sigma_t^2 \mathbf{I}\right) \\ \end{aligned}\]因此条件扩散模型\(p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t,\mathbf{y}\right)\)的采样过程为:
\[\mathbf{x}_{t-1} = \boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right)+\underbrace{\sigma_t^2 \nabla_{\mathbf{x}_t} \log p_{\theta}\left(\mathbf{y} \mid \mathbf{x}_t\right)|_{\mathbf{x}_t=\boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right)}}_{\text{新增项}}+ \sigma_t \mathbf{z},\mathbf{z} \sim \mathcal{N}\left(\mathbf{0}, \mathbf{I}\right)\]⚪ 连续形式的事后修改
对于前向扩散SDE:
\[d \mathbf{x} = \mathbf{f}_t(\mathbf{x})dt+g_t d\mathbf{w}\]对应的反向扩散SDE为:
\[d \mathbf{x} = [\mathbf{f}_t(\mathbf{x})-g_t^2\nabla_{\mathbf{x}} \log p_t(\mathbf{x})]dt+g_t d\mathbf{w}\]条件扩散模型需要把\(p_t(\mathbf{x})\)替换为\(p_t(\mathbf{x} \mid \mathbf{y})\)。根据贝叶斯定理:
\[\begin{aligned} \nabla_{\mathbf{x}} \log p_t(\mathbf{x}\mid \mathbf{y})&=\nabla_{\mathbf{x}} \log \frac{p_t(\mathbf{y}\mid \mathbf{x})p_t(\mathbf{x})}{p_t(\mathbf{y})} \\ &=\nabla_{\mathbf{x}} \log p_t(\mathbf{y}\mid \mathbf{x})+\nabla_{\mathbf{x}} \log p_t(\mathbf{x}) \\ \end{aligned}\]在一般的参数化下有:
\[\begin{aligned} \nabla_{\mathbf{x}_t} \log p_t(\mathbf{x}) = -\frac{\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)}{\sqrt{1-\bar{\alpha}_t}} \end{aligned}\]因此:
\[\begin{aligned} \nabla_{\mathbf{x}} \log p_t(\mathbf{x}\mid \mathbf{y})&=\nabla_{\mathbf{x}} \log p_t(\mathbf{y}\mid \mathbf{x})-\frac{\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)}{\sqrt{1-\bar{\alpha}_t}} \\ &=-\frac{\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)-\sqrt{1-\bar{\alpha}_t}\nabla_{\mathbf{x}} \log p_t(\mathbf{y}\mid \mathbf{x})}{\sqrt{1-\bar{\alpha}_t}} \\ \end{aligned}\]因此只需要用\(\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)-\sqrt{1-\bar{\alpha}_t}\nabla_{\mathbf{x}} \log p_t(\mathbf{y}\mid \mathbf{x})\)替换\(\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\)即可实现条件控制生成:
\[\overline{\boldsymbol{\epsilon}}_\theta\left(\mathbf{x}_t, t\right) = \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)-\sqrt{1-\bar{\alpha}_t}\nabla_{\mathbf{x}} \log p_t(\mathbf{y}\mid \mathbf{x})\]为了控制事后修改的程度,引入分类器引导尺度 (classifier guidance scale) $w$:
\[\overline{\boldsymbol{\epsilon}}_\theta\left(\mathbf{x}_t, t\right) = \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)-\sqrt{1-\bar{\alpha}_t}w\nabla_{\mathbf{x}} \log p_t(\mathbf{y}\mid \mathbf{x})\]分类器引导尺度$w$越大,模型倾向于生成更具有确定性的结果。
⚪ 基于事后修改的条件扩散模型
| 模型 | 采样过程 |
|---|---|
| Classifier Guidance | \(\mathbf{x}_{t-1} = \boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right)+\sigma_t^2 \gamma \nabla_{\mathbf{x}_t} \log p_{\theta}\left(\mathbf{y} \mid \mathbf{x}_t\right)|_{\mathbf{x}_t=\boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right)}+ \sigma_t \mathbf{z},\mathbf{z} \sim \mathcal{N}\left(\mathbf{0}, \mathbf{I}\right)\) |
| Semantic Diffusion Guidance | \(\mathbf{x}_{t-1} = \boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right)+\sigma_t^2 \gamma \nabla_{\mathbf{x}_t} \text{sim}(\mathbf{x}_t,\mathbf{y})|_{\mathbf{x}_t=\boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right)}+ \sigma_t \mathbf{z},\mathbf{z} \sim \mathcal{N}\left(\mathbf{0}, \mathbf{I}\right)\) |
(2)事前训练 Classifier-Free
事前训练是指在扩散模型的训练过程中引入条件信号。这类模型的主要缺点是重新训练扩散模型的成本较大,在预算充裕的前提下,这类模型生成的图像通常具有较好的细节。
注意到反向扩散过程的建模:
\[\begin{aligned} p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)&=\mathcal{N}\left(\mathbf{x}_{t-1} ; \boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right), \sigma_t^2 \mathbf{I}\right) \\ \end{aligned}\]引入输入条件\(\mathbf{y}\)后,定义反向扩散过程:
\[\begin{aligned} p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t,\mathbf{y}\right)&=\mathcal{N}\left(\mathbf{x}_{t-1} ; \boldsymbol{\mu}_\theta\left(\mathbf{x}_t,\mathbf{y}, t\right), \sigma_t^2 \mathbf{I}\right) \\ \end{aligned}\]一般把\(\boldsymbol{\mu}_\theta\)表示为\(\boldsymbol{\epsilon}_\theta\)的函数:
\[\boldsymbol{\mu}_\theta\left(\mathbf{x}_t,\mathbf{y}, t\right) = \frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t,\mathbf{y}, t\right)\right)\]对应训练的损失函数:
\[\begin{aligned} \mathbb{E}_{t \sim[1, T], \mathbf{x}_0, \mathbf{y},\epsilon_t}\left[\left\|\boldsymbol{\epsilon}_t-\boldsymbol{\epsilon}_\theta\left(\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}_t,\mathbf{y}, t\right)\right\|^2\right]\end{aligned}\]此时应把噪声估计器\(\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t,\mathbf{y}, t\right)\)建模为条件输入模型,如通过交叉注意力机制实现。
⚪ 讨论:事后修改与事前训练的关系
注意到:
\[\begin{aligned} \nabla_{\mathbf{x}} \log p_t(\mathbf{y}\mid \mathbf{x})&=\nabla_{\mathbf{x}} \log p_t(\mathbf{x}\mid \mathbf{y})-\nabla_{\mathbf{x}} \log p_t(\mathbf{x}) \\ &= -\frac{\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t,y\right)}{\sqrt{1-\bar{\alpha}_t}}-\frac{\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)}{\sqrt{1-\bar{\alpha}_t}} \\ &= -\frac{1}{\sqrt{1-\bar{\alpha}_t}}\left(\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t,y\right)-\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right) \end{aligned}\]对于事后修改的条件扩散模型,其噪声估计器$\boldsymbol{\epsilon}_\theta$表示为:
\[\overline{\boldsymbol{\epsilon}}_\theta\left(\mathbf{x}_t, t\right) = \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)-\sqrt{1-\bar{\alpha}_t}w\nabla_{\mathbf{x}} \log p_t(\mathbf{y}\mid \mathbf{x})\]向噪声估计器$\boldsymbol{\epsilon}_\theta$中引入条件$\mathbf{y}$,有:
\[\begin{aligned} \overline{\boldsymbol{\epsilon}}_\theta\left(\mathbf{x}_t, t,\mathbf{y}\right) &= \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t,\mathbf{y}\right)-\sqrt{1-\bar{\alpha}_t}w\nabla_{\mathbf{x}} \log p_t(\mathbf{y}\mid \mathbf{x}) \\ &= \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t,\mathbf{y}\right)+w\left(\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t,y\right)-\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right) \\ &= (1+w)\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t,\mathbf{y}\right) - w\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\\ &=s\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t,\mathbf{y}\right) +(1-s) \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right) \end{aligned}\]此时$s = 1+w\geq 1$被称作无分类器引导尺度(classifier-free guidance scale, CFG scale)。因此通过在有标签和无标签的扩散模型的预测之间进行插值,可以实现类似于事后修改使用分类器梯度将样本引导至标签的效果。
注意到\(\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t,\mathbf{y}\right)\)和\(\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\)可以用同一个模型表示:\(\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)=\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t,\mathbf{y}=\phi\right)\);因此在训练时以一定的概率丢弃条件,使得模型同时学习两种情况。
⚪ 基于事前训练的条件扩散模型
| 模型 | 噪声预测器 |
|---|---|
| Classifier Free | \(\tilde{\boldsymbol{\epsilon}}_\theta\left(\mathbf{x}_t,\mathbf{y}, t\right) = (1+w) \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t,\mathbf{y}, t\right) - w\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\) |
| GLIDE | \(\overline{\boldsymbol{\epsilon}}_\theta\left(\mathbf{x}_t \mid c\right) =s\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t\mid c\right) +(1-s) \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t\mid \phi \right)\) |
5. 生成扩散模型的优化
(1)高分辨率图像生成
⚪ DALL-E 2
DALL-E 2模型通过CLIP模型找到文本特征与图像特征的对应关系,然后训练一个prior模型将文本特征转换为图像特征,再训练一个decoder模型(条件扩散模型GLIDE)根据图像特征生成图像。

⚪ Imagen
Imagen模型采用仅在文本数据上训练的大型冻结语言模型T5-XXL编码文本嵌入序列,并将其为条件输入64×64文本图像扩散模型与两个256×256和1024×1024的超分辨率扩散模型。

⚪ Latent Diffusion Model (LDM)
隐扩散模型(latent diffusion model)没有直接在高维图像空间中执行扩散,而是首先使用变分自编码器把图像压缩到隐空间,再在隐空间中构造扩散过程。

⚪ SDXL
SDXL模型是一个二阶段的级联扩散模型,包括Base模型和Refiner模型。其中Base模型是基本的文生图模型;在Base模型之后级联的Refiner模型是图生图模型,用于对Base模型生成的图像隐特征进行精细化。

(2)采样加速
⚪ Score identity Distillation (SiD)
SiD提出了一种将扩散模型蒸馏为单步生成模型的方案:通过学生模型$x=g_\theta(z)$采样数据并训练扩散模型$\epsilon_\psi(x_t,t)$,并最小化其与教师扩散模型$\epsilon_\phi(x_t,t)$的差异。上述两个目标交替优化:
\[\begin{aligned} \psi^* &= \mathop{\arg\min}_\psi\mathbb{E}_{t \sim[1, T], z, \epsilon_t \sim \mathcal{N}(0,I)}\left[\left\|\boldsymbol{\epsilon}_t-\boldsymbol{\epsilon}_\psi\left(\sqrt{\bar{\alpha}_t} g_\theta(z)+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}_t, t\right)\right\|^2\right] \\ \theta^* &= \mathop{\arg\min}_\theta\mathbb{E}_{t \sim[1, T], z, \epsilon_t \sim \mathcal{N}(0,I)}\left[\left<\boldsymbol{\epsilon}_\phi\left(x_t^{(g)}, t\right)-\boldsymbol{\epsilon}_\psi\left(x_t^{(g)}, t\right), \boldsymbol{\epsilon}_\phi\left(x_t^{(g)}, t\right)-\boldsymbol{\epsilon}_t\right>\right] \end{aligned}\]⭐ 参考文献
- 生成扩散模型漫谈(苏剑林):介绍扩散模型的中文系列博客。
- What are Diffusion Models?(Lil’Log):一篇介绍扩散模型的英文博客。
- denoising-diffusion-pytorch(GitHub):Implementation of Denoising Diffusion Probabilistic Model in Pytorch。
- Denoising Diffusion Probabilistic Models:(arXiv2006)DDPM:去噪扩散概率模型。
- Denoising Diffusion Implicit Models:(arXiv2010)DDIM:去噪扩散隐式模型。
- Score-Based Generative Modeling through Stochastic Differential Equations:(arXiv2011)基于得分匹配的随机微分方程生成式建模。
- Improved Denoising Diffusion Probabilistic Models:(arXiv2102)改进的去噪扩散概率模型。
- Variational Diffusion Models:(arXiv2105)在图像合成任务上扩散模型超越了生成对抗网络。
- Diffusion Models Beat GANs on Image Synthesis:(arXiv2107)变分扩散模型。
- More Control for Free! Image Synthesis with Semantic Diffusion Guidance:(arXiv2112)基于语义扩散引导的图像合成。
- High-Resolution Image Synthesis with Latent Diffusion Models:(arXiv2112)通过隐扩散模型实现高分辨率图像合成。
- GLIDE: Towards Photorealistic Image Generation and Editing with Text-Guided Diffusion Models:(arXiv2112)GLIDE:通过文本引导的扩散模型实现真实图像生成与编辑。
- Analytic-DPM: an Analytic Estimate of the Optimal Reverse Variance in Diffusion Probabilistic Models:(arXiv2201)Analytic-DPM:扩散概率模型中最优反向方差的分析估计。
- Hierarchical Text-Conditional Image Generation with CLIP Latents:(arXiv2204)通过CLIP隐特征实现层次化文本条件图像生成。
- Photorealistic Text-to-Image Diffusion Models with Deep Language Understanding:(arXiv2205)通过深度语言理解实现真实文本图像扩散模型。
- Estimating the Optimal Covariance with Imperfect Mean in Diffusion Probabilistic Models:(arXiv2206)扩散概率模型中具有不准确均值的最优协方差估计。
- Classifier-Free Diffusion Guidance:(arXiv2207)无分类器引导的条件扩散模型。
- Cold Diffusion: Inverting Arbitrary Image Transforms Without Noise:(arXiv2208)Cold Diffusion:反转任意无噪声的图像变换。
- Flow Straight and Fast: Learning to Generate and Transfer Data with Rectified Flow:(arXiv2209)通过整流流实现数据的生成与转换。
- Poisson Flow Generative Models:(arXiv2209)泊松流生成模型。
- SDXL: Improving Latent Diffusion Models for High-Resolution Image Synthesis:(arXiv2307)SDXL:改进高分辨率图像合成的隐扩散模型。
- Score identity Distillation: Exponentially Fast Distillation of Pretrained Diffusion Models for One-Step Generation:(arXiv2404)得分恒等蒸馏:单步生成的预训练扩散模型的指数级快速蒸馏。


