改进的去噪扩散概率模型.

• paper：Improved Denoising Diffusion Probabilistic Models

1. 扩散模型

扩散模型 (Diffusion Model)是一类受到非平衡热力学 (non-equilibrium thermodynamics)启发的深度生成模型。这类模型首先定义前向扩散过程的马尔科夫链 (Markov Chain)，向数据中逐渐地添加随机噪声；然后学习反向扩散过程，从噪声中构造所需的数据样本。扩散模型也是一类隐变量模型，其隐变量通常具有较高的维度（与原始数据相同的维度）。

（1）前向扩散过程 forward diffusion process

给定从真实数据分布$q(\mathbf{x})$中采样的数据点$\mathbf{x}_0$~$q(\mathbf{x})$，前向扩散过程定义为逐渐向样本中添加高斯噪声（共计$T$步），从而产生一系列噪声样本$\mathbf{x}_1,…,\mathbf{x}_T$。噪声的添加程度是由一系列方差系数\(\{\beta_t\in (0,1)\}_{t=1}^T\)控制的。

在前向扩散过程中，数据样本$\mathbf{x}_0$逐渐丢失其具有判别性的特征；当$T \to \infty$时，$\mathbf{x}_T$等价于一个各向同性的高斯分布。

使用重参数化技巧，可以采样任意时刻$t$对应的噪声样本$\mathbf{x}_t$。若记$\alpha_t = 1- \beta_t$，则有：

通常在前向扩散过程中会逐渐增大添加噪声的程度，即$\beta_1<\beta_2<\cdots < \beta_T$；因此有$\bar{\alpha}_1>\cdots>\bar{\alpha}_T$。

（2）反向扩散过程 reverse diffusion process

如果能够求得前向扩散过程\(q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)\)的逆过程\(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)\)，则能够从高斯噪声输入\(\mathbf{x}_T \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\)中构造真实样本。注意到当$\beta_t$足够小时，\(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)\)也近似服从高斯分布。然而直接估计\(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)\)是相当困难的，我们在给定数据集的基础上通过神经网络学习条件概率\(p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)\)：

注意到如果额外引入条件\(\mathbf{x}_0\)，则\(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t},\mathbf{x}_0\right)\)是可解的：

其中\(C\left(\mathbf{x}_t, \mathbf{x}_0\right)\)是与\(\mathbf{x}_{t-1}\)无关的项。因此\(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t},\mathbf{x}_0\right)\)也服从高斯分布：

注意到$\mathbf{x}_t=\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}$，因此把$\mathbf{x}_0=(\mathbf{x}_t-\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon})/\sqrt{\bar{\alpha}_t}$代入$\tilde{\boldsymbol{\mu}}_t$可得：

（3）目标函数

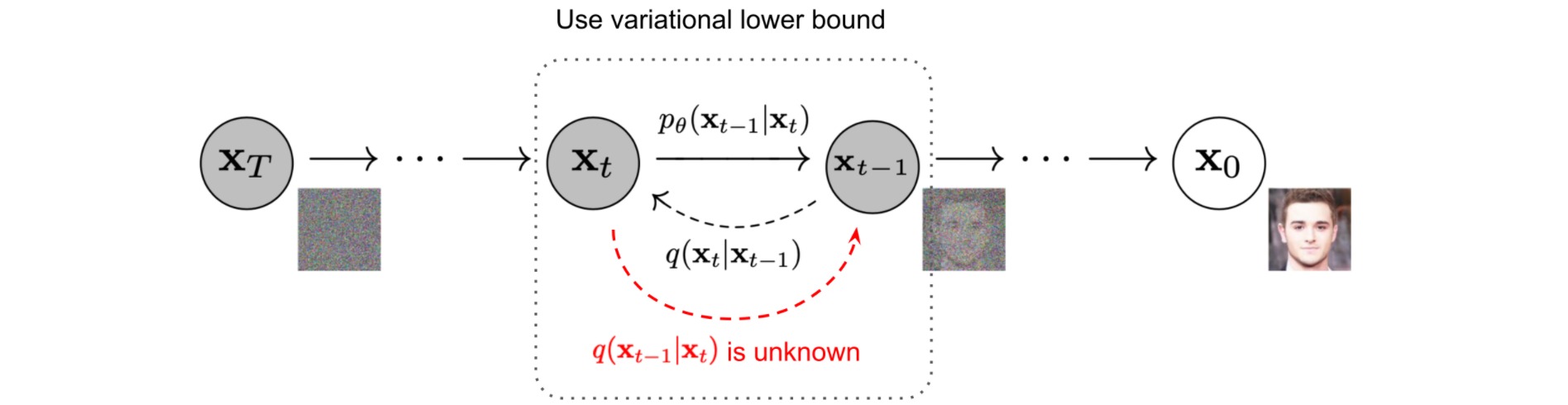
扩散模型的目标函数为最小化\(p_\theta\left(\mathbf{x}_{0}\right)\)的负对数似然\(\log p_\theta\left(\mathbf{x}_0\right)\)：

可以构造负对数似然的负变分下界 (variational lower bound)：

为了把变分下界公式中的每个项转换为可计算的，可以将上述目标进一步重写为几个KL散度项和熵项的组合：

至此，扩散模型的目标函数（负变分下界）可以被分解为$T$项：

其中$L_T$是一个常数（$q$不包含可学习参数$\theta$, $\mathbf{x}_T$是高斯噪声），在训练时可以被省略；$L_0$可以通过一个离散解码器建模；而$L_t$计算了两个高斯分布的KL散度，可以得到闭式解。根据之前的讨论，我们有：

不妨把\(\boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right)\)表示为\(\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\)的函数：

则损失$L_t$可以被表示为\(\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\)和\(\boldsymbol{\Sigma}_\theta\left(\mathbf{x}_t, t\right)\)的函数：

2. 一些改进

（1）参数化 $\beta_{t}$

本文采用基于余弦函数的方差策略。作者指出，策略函数的选择比较灵活，只要在$t=0,t=T$附近具有平缓的改变，而在训练中部有近似线性的变化即可。前向方差$\beta_1,…,\beta_T$设置如下：

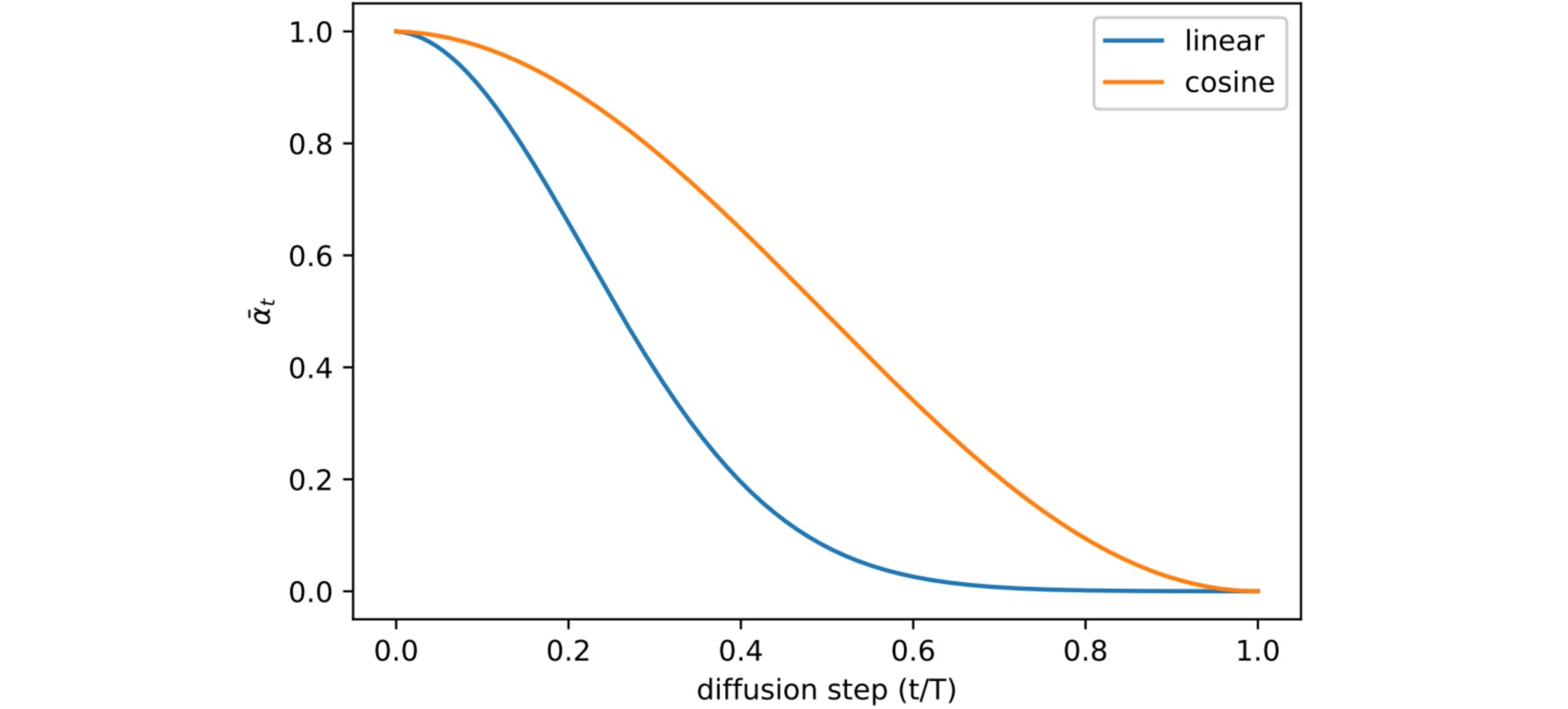
def cosine_beta_schedule(timesteps, s = 0.008):
    steps = timesteps + 1
    t = torch.linspace(0, timesteps, steps, dtype = torch.float64) / timesteps
    alphas_cumprod = torch.cos((t + s) / (1 + s) * math.pi * 0.5) ** 2
    alphas_cumprod = alphas_cumprod / alphas_cumprod[0]
    betas = 1 - (alphas_cumprod[1:] / alphas_cumprod[:-1])
    return torch.clip(betas, 0, 0.999)

（2）参数化 $\Sigma_{\theta}$

本文把$\sigma_t^2$设置为$\beta_t$和\(\tilde{\beta}_t=\frac{1-\overline{\alpha}_{t-1}}{1-\overline{\alpha}_{t}}\cdot \beta_t\)之间的插值结果，通过预测一个混合向量$v$进行插值：

pred_noise, var_interp_frac_unnormalized = model_output.chunk(2, dim = 1)

min_log = extract(self.posterior_log_variance_clipped, t, x.shape)
max_log = extract(torch.log(self.betas), t, x.shape)
var_interp_frac = (var_interp_frac_unnormalized + 1) * 0.5 # [-1,1] -> [0,1]

# \sigma_{\theta}(x_t,t) = exp(v * log \beta_t + (1-v) * \log \tilde{\beta}_t)
model_log_variance = var_interp_frac * max_log + (1 - var_interp_frac) * min_log
model_variance = model_log_variance.exp() 

（3）设置混合损失

原始的损失函数写作：

根据之前的讨论，我们有：

已知两个正态分布\(\mathcal{N}(\mu_1,\sigma_1^2),\mathcal{N}(\mu_2,\sigma_2^2)\)的KL散度计算为$\log \frac{\sigma_2}{\sigma_1}+\frac{\sigma_1^2+(\mu_1-\mu_2)^2}{2\sigma_2^2}-\frac{1}{2}$。因此该损失可以直接计算：

def normal_kl(mean1, logvar1, mean2, logvar2):
    """
    KL divergence between normal distributions parameterized by mean and log-variance.
    """
    return 0.5 * (-1.0 + logvar2 - logvar1 + torch.exp(logvar1 - logvar2) + ((mean1 - mean2) ** 2) * torch.exp(-logvar2))

此外在DDPM模型中，作者使用了简化损失函数：

本文作者设置了一种混合损失函数：

在训练过程中，停止了损失$L_t$中对于$\mu_{\theta}$的梯度计算，即损失$L_t$只会引导$\Sigma_{\theta}$的学习，以增强训练过程的稳定性。

# 计算损失函数
def p_losses(self, x_start, t, noise = None, clip_denoised = False):
    b, c, h, w = x_start.shape
    noise = torch.randn_like(x_start)

    # 计算 x_t
    x_t = self.q_sample(x_start = x_start, t = t, noise = noise)

    # 计算输出 [\epsilon(x_t, t), \sigma_{\theta}(x_t, t)]
    model_output = self.model(x_t, t)
    
    # 计算可学习方差的KL损失 N(\mu(x_t, t), \sigma(x_t, t)) || N(\mu_{\theta}(x_t, t), \sigma_{\theta}(x_t, t))
    true_mean, _, true_log_variance_clipped = self.q_posterior(x_start = x_start, x_t = x_t, t = t)
    model_mean, _, model_log_variance = self.p_mean_variance(x = x_t, t = t, clip_denoised = clip_denoised, model_output = model_output)

    # 计算KL损失时停止\mu_{\theta}(x_t, t)的梯度，提高训练稳定性
    detached_model_mean = model_mean.detach()
    
    kl = normal_kl(true_mean, true_log_variance_clipped, detached_model_mean, model_log_variance)
    kl = torch.mean(kl) / math.log(2)
    
    # 计算 L_0 = - log p_{\theta}(x_0 | x_1)
    decoder_nll = -discretized_gaussian_log_likelihood(x_start, means = detached_model_mean, log_scales = 0.5 * model_log_variance)
    decoder_nll = torch.mean(decoder_nll) / math.log(2)
    
    # T = 0时取解码器的负对数似然，否则取KL散度
    vb_losses = torch.where(t == 0, decoder_nll, kl)
    
    # 计算 L_simple
    pred_noise, _ = model_output.chunk(2, dim = 1)
    simple_losses = F.l1_loss(pred_noise, noise, reduction = 'none')

    return simple_losses.mean() + vb_losses.mean() * self.vb_loss_weight

实践中$L_t$时很难优化的，因此通过重要性采样构造了$L_t$的时序平滑版本。

（4）加速采样

本文提出了交错采样策略(strided sampling schedule)来加速采样过程。该策略每$\lceil T/S \rceil$步进行一次采样更新，从而把总采样次数从$T$次减小为$S$次。

完整的实现代码可参考denoising_diffusion_pytorch。