DDIM:去噪扩散隐式模型.
1. 扩散模型
扩散模型 (Diffusion Model)是一类深度生成模型。这类模型首先定义前向扩散过程的马尔科夫链 (Markov Chain),向数据中逐渐地添加随机噪声;然后学习反向扩散过程,从噪声中构造所需的数据样本。扩散模型也是一类隐变量模型,其隐变量通常具有较高的维度(与原始数据相同的维度)。

(1)前向扩散过程 forward diffusion process
给定从真实数据分布$q(\mathbf{x})$中采样的数据点$\mathbf{x}_0$~$q(\mathbf{x})$,前向扩散过程定义为逐渐向样本中添加高斯噪声(共计$T$步),从而产生一系列噪声样本$\mathbf{x}_1,…,\mathbf{x}_T$。噪声的添加程度是由一系列方差系数\(\{\beta_t\in (0,1)\}_{t=1}^T\)控制的。
\[\begin{aligned} q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)&=\mathcal{N}\left(\mathbf{x}_t ; \sqrt{1-\beta_t} \mathbf{x}_{t-1}, \beta_t \mathbf{I}\right) \\ q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)&=\prod_{t=1}^T q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right) \end{aligned}\]使用重参数化技巧,可以采样任意时刻$t$对应的噪声样本$\mathbf{x}_t$。若记$\alpha_t = 1- \beta_t$,则有:
\[\begin{array}{rlr} \mathbf{x}_t & =\sqrt{\alpha_t} \mathbf{x}_{t-1}+\sqrt{1-\alpha_t} \boldsymbol{\epsilon}_{t-1} \quad ; \text { where } \boldsymbol{\epsilon}_{t-1}, \boldsymbol{\epsilon}_{t-2}, \cdots \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \\ & =\sqrt{\alpha_t \alpha_{t-1}} \mathbf{x}_{t-2}+\sqrt{\alpha_t(1-\alpha_{t-1})} \boldsymbol{\epsilon}_{t-2}+\sqrt{1-\alpha_t} \boldsymbol{\epsilon}_{t-1} \\ & \left( \text { Note that } \mathcal{N}(\mathbf{0}, \alpha_t(1-\alpha_{t-1})) + \mathcal{N}(\mathbf{0}, 1-\alpha_{t}) = \mathcal{N}(\mathbf{0}, 1-\alpha_t\alpha_{t-1}) \right)\\ & =\sqrt{\alpha_t \alpha_{t-1}} \mathbf{x}_{t-2}+\sqrt{1-\alpha_t \alpha_{t-1}} \overline{\boldsymbol{\epsilon}}_{t-2} \\ & =\cdots \\ & =\sqrt{\prod_{i=1}^t \alpha_i} \mathbf{x}_0+\sqrt{1-\prod_{i=1}^t \alpha_i} \boldsymbol{\epsilon} \\ & =\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon} \\ q\left(\mathbf{x}_t \mid \mathbf{x}_0\right) & =\mathcal{N}\left(\mathbf{x}_t ; \sqrt{\bar{\alpha}_t} \mathbf{x}_0,\left(1-\bar{\alpha}_t\right) \mathbf{I}\right) & \end{array}\](2)反向扩散过程 reverse diffusion process
如果能够求得前向扩散过程\(q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)\)的逆过程\(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)\),则能够从高斯噪声输入\(\mathbf{x}_T \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\)中构造真实样本。注意到当$\beta_t$足够小时,\(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)\)也近似服从高斯分布。然而直接估计\(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)\)是相当困难的,我们在给定数据集的基础上通过神经网络学习条件概率\(p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)\):
\[\begin{aligned} p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)&=\mathcal{N}\left(\mathbf{x}_{t-1} ; \boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right), \boldsymbol{\Sigma}_\theta\left(\mathbf{x}_t, t\right)\right)\\ p_\theta\left(\mathbf{x}_{0: T}\right)&=p\left(\mathbf{x}_T\right) \prod_{t=1}^T p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right) \end{aligned}\]注意到如果额外引入条件\(\mathbf{x}_0\),则\(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t},\mathbf{x}_0\right)\)是可解的:
\[\begin{aligned} q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right) & =q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}, \mathbf{x}_0\right) \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_0\right)}{q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)} \\ & \propto \exp \left(-\frac{1}{2}\left(\frac{\left(\mathbf{x}_t-\sqrt{\alpha_t} \mathbf{x}_{t-1}\right)^2}{\beta_t}+\frac{\left(\mathbf{x}_{t-1}-\sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0\right)^2}{1-\bar{\alpha}_{t-1}}-\frac{\left(\mathbf{x}_t-\sqrt{\bar{\alpha}_t} \mathbf{x}_0\right)^2}{1-\bar{\alpha}_t}\right)\right) \\ & =\exp \left(-\frac{1}{2}\left(\frac{\mathbf{x}_t^2-2 \sqrt{\alpha_t} \mathbf{x}_t \mathbf{x}_{t-1}+\alpha_t \mathbf{x}_{t-1}^2}{\beta_t}+\frac{\mathbf{x}_{t-1}^2-2 \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0 \mathbf{x}_{t-1}+\bar{\alpha}_{t-1} \mathbf{x}_0^2}{1-\bar{\alpha}_{t-1}}-\frac{\left(\mathbf{x}_t-\sqrt{\bar{\alpha}_t} \mathbf{x}_0\right)^2}{1-\bar{\alpha}_t}\right)\right) \\ & =\exp \left(-\frac{1}{2}\left(\left(\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar{\alpha}_{t-1}}\right) \mathbf{x}_{t-1}^2-\left(\frac{2 \sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t+\frac{2 \sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}} \mathbf{x}_0\right) \mathbf{x}_{t-1}+C\left(\mathbf{x}_t, \mathbf{x}_0\right)\right)\right) \end{aligned}\]其中\(C\left(\mathbf{x}_t, \mathbf{x}_0\right)\)是与\(\mathbf{x}_{t-1}\)无关的项。因此\(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t},\mathbf{x}_0\right)\)也服从高斯分布:
\[\begin{aligned} q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right) & =\mathcal{N}\left(\mathbf{x}_{t-1} ; \tilde{\boldsymbol{\mu}}\left(\mathbf{x}_t, \mathbf{x}_0\right), \tilde{\beta}_t \mathbf{I}\right) \\ \tilde{\beta}_t & =1 /\left(\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar{\alpha}_{t-1}}\right)=1 /\left(\frac{\alpha_t-\bar{\alpha}_t+\beta_t}{\beta_t\left(1-\bar{\alpha}_{t-1}\right)}\right)=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \cdot \beta_t \\ \tilde{\boldsymbol{\mu}}_t\left(\mathbf{x}_t, \mathbf{x}_0\right) & =\left(\frac{\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}} \mathbf{x}_0\right) /\left(\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar{\alpha}_{t-1}}\right) \\ & =\left(\frac{\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}} \mathbf{x}_0\right) \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \cdot \beta_t \\ & =\frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_t} \mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t} \mathbf{x}_0 \end{aligned}\]注意到$\mathbf{x}_t=\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}$,因此把$\mathbf{x}_0=(\mathbf{x}_t-\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon})/\sqrt{\bar{\alpha}_t}$代入$\tilde{\boldsymbol{\mu}}_t$可得:
\[\begin{aligned} \tilde{\boldsymbol{\mu}}_t & =\frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_t} \mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t} \frac{1}{\sqrt{\bar{\alpha}_t}}\left(\mathbf{x}_t-\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}_t\right) \\ & =\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \epsilon_t\right) \end{aligned}\](3)目标函数
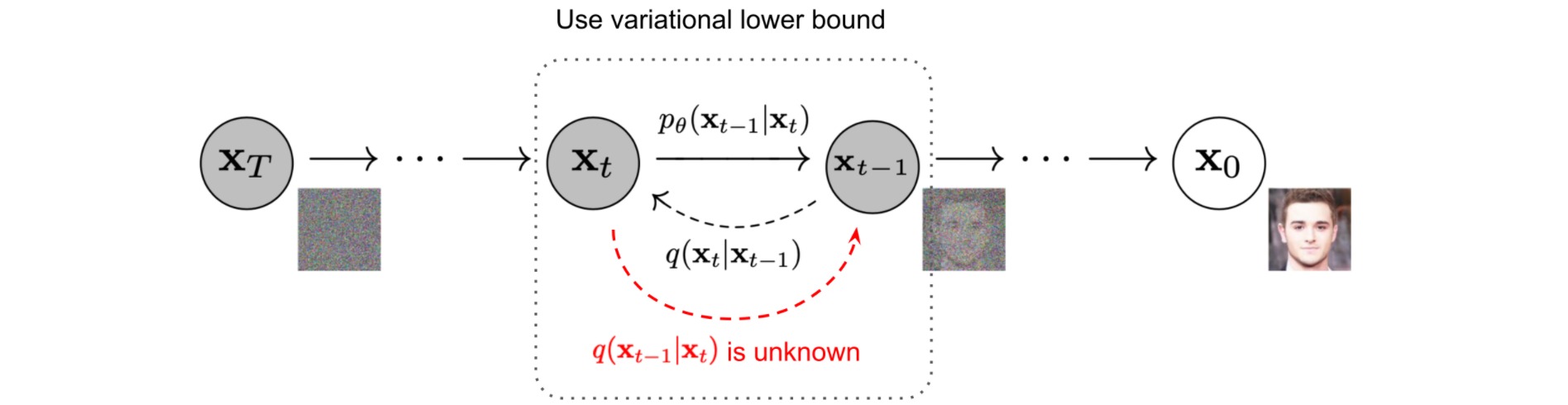
扩散模型的目标函数为最小化\(p_\theta\left(\mathbf{x}_{0}\right)\)的负对数似然\(\log p_\theta\left(\mathbf{x}_0\right)\):
\[\begin{aligned} -\log p_\theta\left(\mathbf{x}_0\right) & \leq-\log p_\theta\left(\mathbf{x}_0\right)+D_{\mathrm{KL}}\left(q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right) \| p_\theta\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)\right) \\ & =-\log p_\theta\left(\mathbf{x}_0\right)+\mathbb{E}_{\mathbf{x}_{1: T} \sim q\left(\mathbf{x}_{\left.1: T\right.} \mid \mathbf{x}_0\right)}\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{0: T}\right) / p_\theta\left(\mathbf{x}_0\right)}\right] \\ & =-\log p_\theta\left(\mathbf{x}_0\right)+\mathbb{E}_q\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{0: T}\right)}+\log p_\theta\left(\mathbf{x}_0\right)\right] \\ & =\mathbb{E}_q\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{0: T}\right)}\right] \\ \end{aligned}\]可以构造负对数似然的负变分下界 (variational lower bound):
\[L_{\mathrm{VLB}}=\mathbb{E}_{q\left(\mathbf{x}_{0: T}\right)}\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{0: T}\right)}\right] \geq-\mathbb{E}_{q\left(\mathbf{x}_0\right)} \log p_\theta\left(\mathbf{x}_0\right)\]为了把变分下界公式中的每个项转换为可计算的,可以将上述目标进一步重写为几个KL散度项和熵项的组合:
\[\begin{aligned} & L_{\mathrm{VLB}}=\mathbb{E}_{q\left(\mathbf{x}_{0: T}\right)}\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{0: T}\right)}\right] \\ & =\mathbb{E}_q\left[\log \frac{\prod_{t=1}^T q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)}{p_\theta\left(\mathbf{x}_T\right) \prod_{t=1}^T p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}\right] \\ & =\mathbb{E}_q\left[-\log p_\theta\left(\mathbf{x}_T\right)+\sum_{t=1}^T \log \frac{q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}\right] \\ & =\mathbb{E}_q\left[-\log p_\theta\left(\mathbf{x}_T\right)+\sum_{t=2}^T \log \frac{q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}+\log \frac{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)}\right] \\ & =\mathbb{E}_q\left[-\log p_\theta\left(\mathbf{x}_T\right)+\sum_{t=2}^T \log \left(\frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)} \cdot \frac{q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)}{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_0\right)}\right)+\log \frac{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)}\right] \\ & =\mathbb{E}_q\left[-\log p_\theta\left(\mathbf{x}_T\right)+\sum_{t=2}^T \log \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}+\sum_{t=2}^T \log \frac{q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)}{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_0\right)}+\log \frac{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)}\right] \\ & =\mathbb{E}_q\left[-\log p_\theta\left(\mathbf{x}_T\right)+\sum_{t=2}^T \log \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}+\log \frac{q\left(\mathbf{x}_T \mid \mathbf{x}_0\right)}{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}+\log \frac{q\left(\mathbf{x}_1 \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)}\right] \\ & =\mathbb{E}_q\left[\log \frac{q\left(\mathbf{x}_T \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_T\right)}+\sum_{t=2}^T \log \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}-\log p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)\right] \\ & =\mathbb{E}_q[\underbrace{D_{\mathrm{KL}}\left(q\left(\mathbf{x}_T \mid \mathbf{x}_0\right) \| p_\theta\left(\mathbf{x}_T\right)\right)}_{L_T}+\sum_{t=2}^T \underbrace{D_{\mathrm{KL}}\left(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right) \| p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)\right)}_{L_{t-1}}-\underbrace{\log p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)}_{L_0}] \\ \end{aligned}\]至此,扩散模型的目标函数(负变分下界)可以被分解为$T$项:
\[\begin{aligned} L_{\mathrm{VLB}} & =L_T+L_{T-1}+\cdots+L_0 \\ \text { where } L_T & =D_{\mathrm{KL}}\left(q\left(\mathbf{x}_T \mid \mathbf{x}_0\right) \| p_\theta\left(\mathbf{x}_T\right)\right) \\ L_t & =D_{\mathrm{KL}}\left(q\left(\mathbf{x}_t \mid \mathbf{x}_{t+1}, \mathbf{x}_0\right) \| p_\theta\left(\mathbf{x}_t \mid \mathbf{x}_{t+1}\right)\right) \text { for } 1 \leq t \leq T-1 \\ L_0 & =-\log p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right) \end{aligned}\]其中$L_T$是一个常数($q$不包含可学习参数$\theta$, $\mathbf{x}_T$是高斯噪声),在训练时可以被省略;$L_0$可以通过一个离散解码器建模;而$L_t$计算了两个高斯分布的KL散度,可以得到闭式解。根据之前的讨论,我们有:
\[\begin{aligned} p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)&=\mathcal{N}\left(\mathbf{x}_{t-1} ; \boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right), \boldsymbol{\Sigma}_\theta\left(\mathbf{x}_t, t\right)\right)\\ q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right) & =\mathcal{N}\left(\mathbf{x}_{t-1} ; \frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \epsilon_t\right), \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \cdot \beta_t \mathbf{I}\right) \end{aligned}\]不妨把\(\boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right)\)表示为\(\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\)的函数:
\[\boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right) = \frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right)\]则损失$L_t$可以被表示为\(\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\)和\(\boldsymbol{\Sigma}_\theta\left(\mathbf{x}_t, t\right)\)的函数:
\[\begin{aligned} L_t & =\mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}}\left[\frac{1}{2\left\|\boldsymbol{\Sigma}_\theta\left(\mathbf{x}_t, t\right)\right\|_2^2}\left\|\tilde{\boldsymbol{\mu}}_t\left(\mathbf{x}_t, \mathbf{x}_0\right)-\boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right)\right\|^2\right] \\ & =\mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}}\left[\frac{1}{2\left\|\boldsymbol{\Sigma}_\theta\right\|_2^2}\left\|\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_t\right)-\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right)\right\|^2\right] \\ & =\mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}}\left[\frac{\left(1-\alpha_t\right)^2}{2 \alpha_t\left(1-\bar{\alpha}_t\right)\left\|\boldsymbol{\Sigma}_\theta\right\|_2^2}\left\|\boldsymbol{\epsilon}_t-\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right\|^2\right] \\ & =\mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}}\left[\frac{\left(1-\alpha_t\right)^2}{2 \alpha_t\left(1-\bar{\alpha}_t\right)\left\|\boldsymbol{\Sigma}_\theta\right\|_2^2}\left\|\boldsymbol{\epsilon}_t-\boldsymbol{\epsilon}_\theta\left(\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}_t, t\right)\right\|^2\right] \end{aligned}\]在DDPM模型中,作者使用了简化损失函数:
\[\begin{aligned} L_t^{\text {simple }} =\mathbb{E}_{t \sim[1, T], \mathbf{x}_0, \epsilon_t}\left[\left\|\boldsymbol{\epsilon}_t-\boldsymbol{\epsilon}_\theta\left(\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}_t, t\right)\right\|^2\right] \end{aligned}\]2. DDIM
(1)DDIM的建模
在扩散模型中,前向传播只依赖于\(q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)\),而不必具体到定义\(q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)\)。因此不妨跳过\(q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)\),直接定义:
\[\begin{array}{rlr} \mathbf{x}_t & =\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon} \\ q\left(\mathbf{x}_t \mid \mathbf{x}_0\right) & =\mathcal{N}\left(\mathbf{x}_t ; \sqrt{\bar{\alpha}_t} \mathbf{x}_0,\left(1-\bar{\alpha}_t\right) \mathbf{I}\right) & \end{array}\]此时\(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t},\mathbf{x}_0\right)\)并不是可解的(因为\(q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}, \mathbf{x}_0\right)\)是未知的):
\[\begin{aligned} q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right) & =q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}, \mathbf{x}_0\right) \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_0\right)}{q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)} \\ \end{aligned}\]我们不妨将其建模为一个高斯分布,注意此时$\sigma_t$是人为指定的:
\[\begin{aligned} q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)&=\mathcal{N}\left(\mathbf{x}_{t-1} ; \kappa_t\mathbf{x}_{t}+\lambda_t \mathbf{x}_0, \sigma_t^2 \mathbf{I}\right) \end{aligned}\]此时前向扩散过程不再是一个马尔科夫链:

对上述分布进行重参数化:
\[\begin{array}{rlr} \mathbf{x}_{t-1} &=\kappa_t\mathbf{x}_{t}+\lambda_t \mathbf{x}_0 + \sigma_t \boldsymbol{\epsilon}_2 \\ & = \kappa_t (\sqrt{\bar{\alpha}_{t}} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_{t}} \boldsymbol{\epsilon}_1)+\lambda_t \mathbf{x}_0 + \sigma_t \boldsymbol{\epsilon}_2 \\ & = (\kappa_t \sqrt{\bar{\alpha}_{t}} + \lambda_t) \mathbf{x}_0+(\kappa_t \sqrt{1-\bar{\alpha}_{t}} \boldsymbol{\epsilon}_1+ \sigma_t \boldsymbol{\epsilon}_2) \\ & = (\kappa_t \sqrt{\bar{\alpha}_{t}} + \lambda_t) \mathbf{x}_0+\sqrt{\kappa_t^2(1-\bar{\alpha}_{t})+\sigma_t^2} \boldsymbol{\epsilon} \end{array}\]而根据前向扩散过程可以得到:
\[\begin{array}{rlr} \mathbf{x}_{t-1} =\sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_{t-1}} \boldsymbol{\epsilon} \end{array}\]联立上述两个方程可以得到:
\[\begin{aligned} \kappa_t = \sqrt{\frac{1-\bar{\alpha}_{t-1}-\sigma_t^2}{1-\bar{\alpha}_{t}}} , \quad \lambda_t = \sqrt{\bar{\alpha}_{t-1}} - \sqrt{\frac{\bar{\alpha}_{t}(1-\bar{\alpha}_{t-1}-\sigma_t^2)}{1-\bar{\alpha}_{t}}} \end{aligned}\]因此得到:
\[\begin{aligned} \mathbf{x}_{t-1} = \sqrt{\frac{1-\bar{\alpha}_{t-1}-\sigma_t^2}{1-\bar{\alpha}_{t}}}\mathbf{x}_{t}+\left( \sqrt{\bar{\alpha}_{t-1}} - \sqrt{\frac{\bar{\alpha}_{t}(1-\bar{\alpha}_{t-1}-\sigma_t^2)}{1-\bar{\alpha}_{t}}} \right) \mathbf{x}_0+ \sigma_t \boldsymbol{\epsilon}_t \end{aligned}\]注意到$\mathbf{x}_0=(\mathbf{x}_t-\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon})/\sqrt{\bar{\alpha}_t}$,上式进一步表示为:
\[\begin{aligned} \mathbf{x}_{t-1} &= \sqrt{\frac{1-\bar{\alpha}_{t-1}-\sigma_t^2}{1-\bar{\alpha}_{t}}}\mathbf{x}_{t}+\left( \sqrt{\bar{\alpha}_{t-1}} - \sqrt{\frac{\bar{\alpha}_{t}(1-\bar{\alpha}_{t-1}-\sigma_t^2)}{1-\bar{\alpha}_{t}}} \right) \frac{\mathbf{x}_t-\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}}{\sqrt{\bar{\alpha}_t}}+ \sigma_t \boldsymbol{\epsilon}_t \\ &= \frac{1}{\sqrt{\alpha_t}}\mathbf{x}_{t}+\left( \sqrt{1-\bar{\alpha}_{t-1}-\sigma_t^2}-\frac{\sqrt{1-\bar{\alpha}_t}}{\sqrt{\alpha_t}} \right) \boldsymbol{\epsilon}+ \sigma_t \boldsymbol{\epsilon}_t \end{aligned}\]因此得到:
\[\begin{aligned} q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)&=\mathcal{N}\left(\mathbf{x}_{t-1} ; \frac{1}{\sqrt{\alpha_t}}\mathbf{x}_{t}+\left( \sqrt{1-\bar{\alpha}_{t-1}-\sigma_t^2}-\frac{\sqrt{1-\bar{\alpha}_t}}{\sqrt{\alpha_t}} \right) \boldsymbol{\epsilon}, \sigma_t^2 \mathbf{I}\right) \end{aligned}\](2)DDIM的目标函数
我们在给定数据集的基础上通过神经网络学习条件概率\(p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)\):
\[\begin{aligned} p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)&=\mathcal{N}\left(\mathbf{x}_{t-1} ; \boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right), \boldsymbol{\Sigma}_\theta\left(\mathbf{x}_t, t\right)\right) \end{aligned}\]不妨把\(\boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right)\)表示为\(\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\)的函数:
\[\boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right) = \frac{1}{\sqrt{\alpha_t}}\mathbf{x}_{t}+\left( \sqrt{1-\bar{\alpha}_{t-1}-\sigma_t^2}-\frac{\sqrt{1-\bar{\alpha}_t}}{\sqrt{\alpha_t}} \right) \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\]进而构造损失函数,若忽略权重项,则损失与DDPM一致:
\[\begin{aligned} L_t^{\text {simple }} =\mathbb{E}_{t \sim[1, T], \mathbf{x}_0, \epsilon_t}\left[\left\|\boldsymbol{\epsilon}_t-\boldsymbol{\epsilon}_\theta\left(\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}_t, t\right)\right\|^2\right] \end{aligned}\]这是因为前向传播过程\(q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)\)没有进行改动,因此DDIM的训练过程没有改变,可以直接使用DDPM训练好的模型。
(3)DDIM的采样
DDIM的采样过程:
\[\begin{aligned} \mathbf{x}_{t-1} &= \frac{1}{\sqrt{\alpha_t}}\mathbf{x}_{t}+\left( \sqrt{1-\bar{\alpha}_{t-1}-\sigma_t^2}-\frac{\sqrt{1-\bar{\alpha}_t}}{\sqrt{\alpha_t}} \right) \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)+ \sigma_t \boldsymbol{\epsilon} \\ & = \sqrt{\bar{\alpha}_{t-1}}\left(\frac{\mathbf{x}_{t}-\sqrt{1-\bar{\alpha}_t}\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)}{\sqrt{\bar{\alpha}_t}}\right)+ \sqrt{1-\bar{\alpha}_{t-1}-\sigma_t^2} \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)+ \sigma_t\mathbf{\epsilon} \\ & = \sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_{0}+ \sqrt{1-\bar{\alpha}_{t-1}-\sigma_t^2} \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)+ \sigma_t \boldsymbol{\epsilon} \end{aligned}\]采样过程中存在可变动参数$\sigma_t$,不同的取值能够产生不同的采样结果。
若取\(\sigma_t^2=\frac{1-\overline{\alpha}_{t-1}}{1-\overline{\alpha}_{t}}\cdot \beta_t\),则有:
\[\begin{aligned} \mathbf{x}_{t-1} &= \frac{1}{\sqrt{\alpha_t}}\mathbf{x}_{t}+\left( \sqrt{1-\bar{\alpha}_{t-1}-\frac{1-\overline{\alpha}_{t-1}}{1-\overline{\alpha}_{t}}\cdot \beta_t}-\frac{\sqrt{1-\bar{\alpha}_t}}{\sqrt{\alpha_t}} \right) \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)+ \sigma_t \boldsymbol{\epsilon} \\ &= \frac{1}{\sqrt{\alpha_t}}\mathbf{x}_{t}+\frac{\alpha_t-1}{\sqrt{\alpha_t \cdot (1-\bar{\alpha}_{t})}} \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)+ \sigma_t \boldsymbol{\epsilon} \\ &= \frac{1}{\sqrt{\alpha_t}} \left( \mathbf{x}_{t}-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_{t}}} \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right) \right)+ \sigma_t \boldsymbol{\epsilon} \end{aligned}\]此即为DDPM的采样过程。一般地,作者指定\(\sigma_t^2=\eta \frac{1-\overline{\alpha}_{t-1}}{1-\overline{\alpha}_{t}}\cdot \beta_t\),其中$\eta \in [0,1]$控制采样过程的随机性。当$\eta=0$即\(\sigma_t^2=0\)时,此时从\(\mathbf{x}_{t}\)到\(\mathbf{x}_{t-1}\)是一个确定性变换:
\[\begin{aligned} \mathbf{x}_{t-1} &= \frac{1}{\sqrt{\alpha_t}}\mathbf{x}_{t}+\left( \sqrt{1-\bar{\alpha}_{t-1}}-\frac{\sqrt{1-\bar{\alpha}_t}}{\sqrt{\alpha_t}} \right) \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right) \\ &= \frac{1}{\sqrt{\alpha_t}} \left( \mathbf{x}_{t}-\left(\sqrt{1-\bar{\alpha}_t}- \sqrt{\alpha_t-\bar{\alpha}_{t}} \right) \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right) \right) \end{aligned}\]此时反向扩散过程(即生成过程)从一个概率生成模型退化为一个概率判别模型,等价于将任意正态噪声向量变换为图片的一个确定性变换。此时我们可以对噪声向量进行插值,然后观察对应的生成效果。但要注意的是,扩散模型对噪声分布比较敏感,所以不能用线性插值而要用球面插值,因为由正态分布的叠加性,如果$z_1,z_2∼N(0,I)$,$λz_1+(1−λ)z_2$一般就不服从$N(0,I)$,要改为:
\[z = z_1 \cos \frac{\lambda \pi}{2}+z_2 \sin \frac{\lambda \pi}{2}, \lambda \in [0,1]\]
相比于DDPM,DDIM的生成过程具有判别性($\sigma_t=0$),这意味着以同一隐变量为条件的多个生成样本应该具有类似的高级特征。由于这种一致性,DDIM可以在隐变量空间中进行在语义上有意义的插值。
此外,作者指出DDPM的训练结果实质上包含了它的任意子序列参数的训练结果。设$τ=[τ_1,τ_2,…,τ_{dim(τ)}]$是$[1,2,⋯,T]$的任意子序列,则以\(\bar{\alpha}_{τ_1},\bar{\alpha}_{τ_2},...,\bar{\alpha}_{τ_{dim(τ)}}\)为参数训练一个扩散步数为$dim(τ)$步的DDPM,其目标函数实际上是原来以\(\bar{\alpha}_{1},\bar{\alpha}_{2},...,\bar{\alpha}_{T}\)的$T$步DDPM的目标函数的一个子集。所以在模型拟合能力足够好的情况下,它其实包含了任意子序列参数的训练结果。因此在采样时,可以按照步数$[τ_1,τ_2,…,τ_{dim(τ)}]$进行采样,从而加速采样过程。

相比于DDPM,DDIM在设置更少的采样步数时具有更高的生成质量。
(4)DDIM的实现
DDIM完整的实现代码可参考denoising_diffusion_pytorch。
class GaussianDiffusion(nn.Module):
def __init__(
self,
model,
*,
image_size,
timesteps = 1000,
sampling_timesteps = None,
ddim_sampling_eta = 0.,
):
super().__init__()
self.model = model # 用于拟合\epsilon(x_t,t)的神经网络
self.channels = self.model.channels
self.image_size = image_size
betas = cosine_beta_schedule(timesteps) # \beta_t
alphas = 1. - betas # \alpha_t
alphas_cumprod = torch.cumprod(alphas, dim=0) # \bar{\alpha}_t
alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value = 1.) # \bar{\alpha}_{t-1}
self.num_timesteps = int(timesteps)
self.alphas_cumprod = alphas_cumprod
# sampling related parameters
self.sampling_timesteps = default(sampling_timesteps, timesteps) # default num sampling timesteps to number of timesteps at training
assert self.sampling_timesteps <= timesteps
self.ddim_sampling_eta = ddim_sampling_eta
# helper function to register buffer from float64 to float32
register_buffer = lambda name, val: self.register_buffer(name, val.to(torch.float32))
register_buffer('betas', betas)
# calculations for diffusion q(x_t | x_{t-1}) and others
register_buffer('sqrt_alphas_cumprod', torch.sqrt(alphas_cumprod)) # \sqrt{\bar{\alpha}_t}
register_buffer('sqrt_one_minus_alphas_cumprod', torch.sqrt(1. - alphas_cumprod)) # \sqrt{1-\bar{\alpha}_t}
register_buffer('log_one_minus_alphas_cumprod', torch.log(1. - alphas_cumprod)) # \log{1-\bar{\alpha}_t}
register_buffer('sqrt_recip_alphas_cumprod', torch.sqrt(1. / alphas_cumprod)) # \sqrt{1/\bar{\alpha}_t}
register_buffer('sqrt_recipm1_alphas_cumprod', torch.sqrt(1. / alphas_cumprod - 1)) # \sqrt{1/(\bar{\alpha}_t-1)}
# calculations for posterior q(x_{t-1} | x_t, x_0)
posterior_variance = betas * (1. - alphas_cumprod_prev) / (1. - alphas_cumprod) # \sigma_t
register_buffer('posterior_variance', posterior_variance)
# log calculation clipped because the posterior variance is 0 at the beginning of the diffusion chain
register_buffer('posterior_log_variance_clipped', torch.log(posterior_variance.clamp(min =1e-20)))
register_buffer('posterior_mean_coef1', betas * torch.sqrt(alphas_cumprod_prev) / (1. - alphas_cumprod))
register_buffer('posterior_mean_coef2', (1. - alphas_cumprod_prev) * torch.sqrt(alphas) / (1. - alphas_cumprod))
"""
Training
"""
# 计算x_t=\sqrt{\bat{\alpha}_t}x_0+\sqrt{1-\bat{\alpha}_t}\epsilon
def q_sample(self, x_start, t, noise=None):
return (
extract(self.sqrt_alphas_cumprod, t, x_start.shape) * x_start +
extract(self.sqrt_one_minus_alphas_cumprod, t, x_start.shape) * noise
)
# 计算损失函数L_t=||\epsilon-\epsilon(x_t, t)||_1
def p_losses(self, x_start, t, noise = None):
b, c, h, w = x_start.shape
noise = torch.randn_like(x_start)
target = noise
# 计算 x_t
x = self.q_sample(x_start = x_start, t = t, noise = noise)
# 计算 \epsilon(x_t, t)
model_out = self.model(x, t)
loss = F.l1_loss(model_out, target, reduction = 'none')
loss = reduce(loss, 'b ... -> b (...)', 'mean')
return loss.mean()
# 训练过程
def forward(self, img, *args, **kwargs):
b, c, h, w, device = *img.shape, img.device
t = torch.randint(0, self.num_timesteps, (b,), device=device).long()
img = img * 2 - 1 # data [0, 1] -> [-1, 1]
return self.p_losses(img, t, *args, **kwargs)
"""
Sampling
"""
# 计算 x_0 = \sqrt{1/\bat{\alpha}_t}x_t-\sqrt{1/(1-\bat{\alpha}_t)}\epsilon_t
def predict_start_from_noise(self, x_t, t, noise):
return (
extract(self.sqrt_recip_alphas_cumprod, t, x_t.shape) * x_t -
extract(self.sqrt_recipm1_alphas_cumprod, t, x_t.shape) * noise
)
@torch.no_grad()
def ddim_sample(self, shape, return_all_timesteps = False):
batch, device, total_timesteps, sampling_timesteps, eta = shape[0], self.betas.device, self.num_timesteps, self.sampling_timesteps, self.ddim_sampling_eta
times = torch.linspace(-1, total_timesteps - 1, steps = sampling_timesteps + 1) # [-1, 0, 1, 2, ..., T-1] when sampling_timesteps == total_timesteps
times = list(reversed(times.int().tolist()))
time_pairs = list(zip(times[:-1], times[1:])) # [(T-1, T-2), (T-2, T-3), ..., (1, 0), (0, -1)]
img = torch.randn(shape, device = device)
imgs = [img]
x_start = None
for time, time_next in tqdm(time_pairs, desc = 'sampling loop time step'):
time_cond = torch.full((batch,), time, device = device, dtype = torch.long)
pred_noise = self.model(img, time_cond) # 计算 \epsilon(x_t, t)
x_start = self.predict_start_from_noise(img, time_cond, pred_noise) # x_0
if time_next < 0:
img = x_start
imgs.append(img)
continue
alpha = self.alphas_cumprod[time]
alpha_next = self.alphas_cumprod[time_next]
sigma = eta * ((1 - alpha / alpha_next) * (1 - alpha_next) / (1 - alpha)).sqrt()
c = (1 - alpha_next - sigma ** 2).sqrt()
noise = torch.randn_like(img)
img = x_start * alpha_next.sqrt() + \
c * pred_noise + \
sigma * noise
imgs.append(img)
ret = img if not return_all_timesteps else torch.stack(imgs, dim = 1)
ret = (ret + 1) * 0.5
return ret
# 采样过程
@torch.no_grad()
def sample(self, batch_size = 16, img_channel = 3, return_all_timesteps = False):
image_size, channels = self.image_size, img_channel
return self.ddim_sample((batch_size, channels, image_size, image_size), return_all_timesteps = return_all_timesteps)


