OctConv:通过八度卷积降低卷积神经网络的空间复杂度.
- paper:Drop an Octave: Reducing Spatial Redundancy in Convolutional Neural Networks with Octave Convolution
1. 尺度空间理论 Scale-Space Theory
如果要处理的图像中目标的尺度(scale)是未知的,则可以采用尺度空间理论。其核心思想是将图像用多种尺度表示,这些表示统称为尺度空间表示(scale-space representation)。其中线性(高斯)尺度空间使用最为广泛。
对图像用一系列高斯滤波器加以平滑,这些高斯滤波器的尺寸是不同的,就得到了该图像在不同尺度下的表示。记二维图像$f(x,y)$,二维高斯函数$g(x,y;t)=\frac{1}{2\pi t}e^{-\frac{x^2+y^2}{2t}}$,其中$t=\sigma^2$是尺度参数(scale parameter)。则线性尺度空间可以通过二者卷积得到:
\[L(\cdot,\cdot;t) = g(x,y;t) * f(x,y)\]图像中尺度小于$\sqrt{t}$的结构会被平滑地无法分辨。因此$t$越大,平滑越剧烈。通常只会考虑$t\geq 0$的一些离散取值;当$t=0$时高斯滤波器退化为脉冲函数(impulse function),因此卷积的结果是图像本身,不作任何平滑。

尺度空间方法具有尺度不变性(scale invariant),因此可以处理未知大小的图像目标。在构造尺度空间时,同时对图像进行降采样。比如$t=2$的尺度空间,会将图像的分辨率减半。
2. 八度卷积 Octave Convolution
本文作者假设,卷积层的输出特征图中存在高、低频分量。其中低频分量支撑的是图像的整体特征,是存在冗余的,在编码过程中可以节省。

作者设计了Octave Convolution取代标准的卷积操作。在音乐中Octave是八音阶的意思,每隔一个八音阶频率会减半;在文中drop an octave就是通道的空间尺寸减半的含义。
Octave Convolution首先构造图像及其特征图的线性尺度表示:把原始特征的$1-\alpha$通道看作高频分量,剩余$\alpha \in [0,1]$通道经过$t=2$的高斯滤波后作为低频分量。由于低频分量是冗余的,因此把低频分量的空间尺寸设置为高频分量空间尺寸的一半。通过调整低频比例$α$,预测精度和计算代价可以得到权衡。
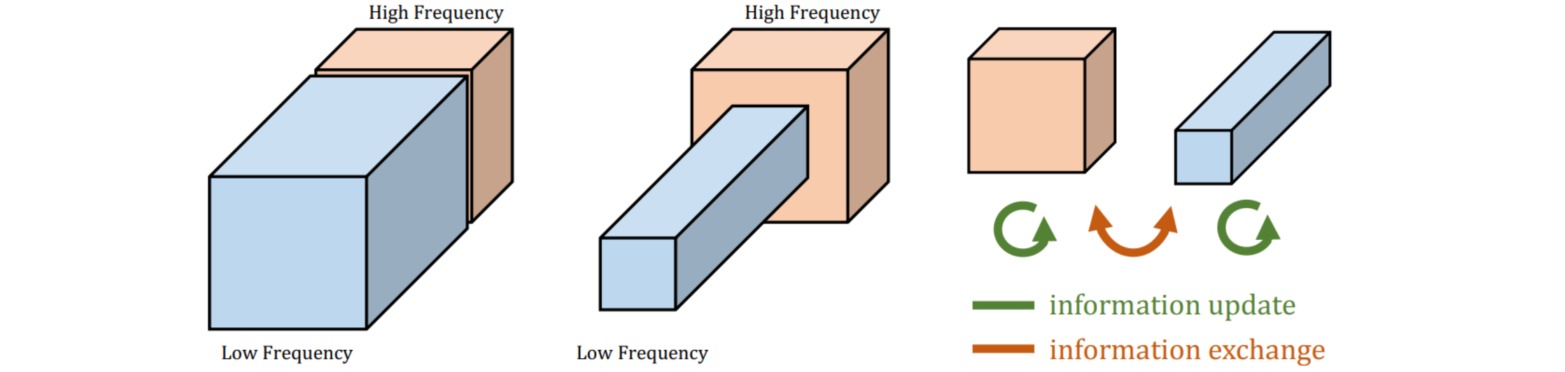
由于高/低频通道的空间尺寸不一致,因此传统卷积无法执行。设图像的低频分量和高频分量分别是$X^L$和$X^H$,卷积输出的低频分量和高频分量分别是$Y^L$和$Y^H$。作者通过四组卷积$W^{H→H},W^{L→L},W^{L→H},W^{H→L}$实现不同频率分量内部的更新和相互交互。
$W^{H→H},W^{L→L}$处理的特征尺寸不变,因此采用标准卷积实现;$W^{H→L}$先对特征进行平均池化,再执行标准卷积;$W^{L→H}$则是先执行标准卷积,再对特征进行空间上采样。
Octave Convolution的实现过程为:
\[\begin{aligned} y^H(p_0)& = \sum_{p_n \in \mathcal{R}} w^{H→H}(p_n) \cdot x^H(p_0+p_n) \\&+ \sum_{p_n \in \mathcal{R}} w^{L→H}(p_n) \cdot x^L(\lfloor \frac{p_0}{2} \rfloor +p_n) \\ y^L(p_0)& = \sum_{p_n \in \mathcal{R}} w^{L→L}(p_n) \cdot x^L(p_0+p_n) \\&+ \sum_{p_n \in \mathcal{R}} w^{H→L}(p_n) \cdot x^H(2 p_0+0.5 +p_n) \end{aligned}\]
Octave Convolution和标准卷积的卷积核尺寸相同($c_{in}\times c_{out} \times k \times k$),因此所具有的参数量相同,在此基础上网络更清晰地分开处理高、低频分量,并且在冗余的低频分量上节约了计算量。

import torch
import torch.nn as nn
import torch.nn.functional as F
class OctaveConv(nn.Module):
def __init__(self, in_channels, out_channels, kernel_size,
alpha_in=0.5, alpha_out=0.5, stride=1,
padding=1, dilation=1, groups=1, bias=False):
super(OctaveConv, self).__init__()
self.weights = nn.Parameter(torch.Tensor(out_channels, in_channels, kernel_size[0], kernel_size[1]))
self.stride = stride
self.padding = padding
self.dilation = dilation
self.groups = groups
if bias:
self.bias = nn.Parameter(torch.Tensor(out_channels))
else:
self.bias = torch.zeros(out_channels)
self.h2g_pool = nn.AvgPool2d(kernel_size=(2,2), stride=2)
self.in_channels = in_channels
self.out_channels = out_channels
self.alpha_in = alpha_in
self.alpha_out = alpha_out
def forward(self, x):
X_h, X_l = x
if self.stride ==2:
X_h, X_l = self.h2g_pool(X_h), self.h2g_pool(X_l)
X_h2l = self.h2g_pool(X_h)
end_h_x = int(self.in_channels*(1- self.alpha_in))
end_h_y = int(self.out_channels*(1- self.alpha_out))
X_h2h = F.conv2d(X_h, self.weights[0:end_h_y, 0:end_h_x, :,:], self.bias[0:end_h_y], 1,
self.padding, self.dilation, self.groups)
X_l2l = F.conv2d(X_l, self.weights[end_h_y:, end_h_x:, :,:], self.bias[end_h_y:], 1,
self.padding, self.dilation, self.groups)
X_h2l = F.conv2d(X_h2l, self.weights[end_h_y:, 0: end_h_x, :,:], self.bias[end_h_y:], 1,
self.padding, self.dilation, self.groups)
X_l2h = F.conv2d(X_l, self.weights[0:end_h_y, end_h_x:, :,:], self.bias[0:end_h_y], 1,
self.padding, self.dilation, self.groups)
X_l2h = F.upsample(X_l2h, scale_factor=2, mode='nearest')
X_h = X_h2h + X_l2h
X_l = X_l2l + X_h2l
return X_h, X_l
x_h = torch.rand((16, 128, 64, 64))
x_l = torch.rand((16, 128, 32, 32))
OCconv = OctaveConv(kernel_size=(3,3),in_channels=256,out_channels=512,stride=2)
print(OCconv((x_h,x_l))[0].shape) # torch.Size([16, 256, 32, 32])
print(OCconv((x_h,x_l))[1].shape) # torch.Size([16, 256, 16, 16])


