Regularization in Deep Learning.
深度学习所处理的问题包括优化问题和泛化问题。优化(optimization)问题是指在已有的数据集上实现最小的训练误差;而泛化(generalization)问题是指在未经过训练的数据集(通常假设与训练集同分布)上实现最小的泛化误差(generalize error)。通常深度神经网络具有很强的拟合能力,因此训练误差较低,但是容易过拟合(overfitting),导致泛化误差较大。
正则化(Regularization)指的是通过引入噪声或限制模型的复杂度,降低模型对输入或者参数的敏感性,避免过拟合,提高模型的泛化能力。常用的正则化方法包括约束目标函数(等价于约束模型参数)、约束网络结构、约束优化过程。
- 约束目标函数:在目标函数中增加模型参数的正则化项,包括L2正则化, L1正则化, 弹性网络正则化, L0正则化, 谱正则化, 自正交性正则化, WEISSI正则化, 梯度惩罚
- 约束网络结构:在网络结构中添加噪声,包括随机深度, Dropout及其系列方法,
- 约束优化过程:在优化过程中施加额外步骤,包括数据增强, 梯度裁剪, Early Stop, 标签平滑, 变分信息瓶颈, 虚拟对抗训练, Flooding
1. 约束目标函数
⚪ L2正则化 L2 Regularization
L2正则化通过约束参数的L2范数(L2-norm)减小过拟合。带有L2正则化的优化问题可写作:
\[w^*= \mathop{\arg\min}_w \frac{1}{N} \sum_{n=1}^{N} {L(y_n,f(x_n);w)}+λ ||w||_2^2\](1) 讨论:L2正则化等价于约束参数矩阵的Frobenius范数
若将模型参数表示为矩阵$W$,则L2正则化等价于约束矩阵$W$的Frobenius范数:
\[\sum_{i,j} w_{ij}^2 = ||W||_F^2\]矩阵$W$的Frobenius范数 $||W||_F$是矩阵的谱范数 $||W||_2$的一个上界。约束Frobenius范数能够使网络更好地满足Lipschitz连续性,从而降低模型对输入扰动的敏感性,增强模型的泛化能力。
下面证明Frobenius范数是谱范数的上界。对于矩阵$W$和向量$x$,根据柯西不等式:
\[||Wx|| \leq ||W||_F \cdot ||x||\]而谱范数的定义:
\[||W||_2 = \mathop{\max}_{x \neq 0} \frac{||Wx||}{||x||}\]因此有:
\[||W||_2 \leq ||W||_F\](2) 讨论:L2正则化等价于参数服从正态分布的最大后验估计
从贝叶斯角度出发,把参数$w$看作随机变量,假设其先验概率$p(w)$服从正态分布$N(0,σ_0^2)$。
由贝叶斯定理可得参数$w$的后验概率$p(w|x,y)$:
\[p(w |x, y) = \frac{p(x,y | w)p(w)}{p(y)} \propto p(x,y | w)p(w)\]参数$w$的最大后验估计为:
\[\begin{aligned} \hat{w} &= \mathop{\arg \max}_{w}\log p(w |x, y) = \mathop{\arg \max}_{w}\log p(x,y | w)p(w) \\ &= \mathop{\arg \max}_{w} \log p(x,y | w) +\log\frac{1}{\sqrt{2\pi}σ_0} \exp(-\frac{w^Tw}{2σ_0^2}) \\ &\propto \mathop{\arg \max}_{w} \log p(x,y | w)-\frac{w^Tw}{2σ_0^2} \\ &= \mathop{\arg \min}_{w} -\log p(x,y | w)+\frac{1}{2σ_0^2}||w||_2^2 \end{aligned}\]因此参数服从正态分布的最大后验估计等价于引入L2正则化。
(3) 讨论:L2正则化与权重衰减
在标准的梯度下降算法中,应用L2正则化后参数的更新过程为:
\[\begin{aligned} w^{(t+1)} &\leftarrow w^{(t)} - \alpha \nabla_w[L(w)+λ ||w||_2^2] \\ &\leftarrow (1-2\alpha \lambda)w^{(t)} - \alpha \nabla_w L(w) \end{aligned}\]上式相当于在参数更新时首先对参数引入一个衰减系数$\alpha \lambda$,因此也称为权重衰减(Weight Decay)正则化。
值得一提的是,在Adam等自适应学习率算法中,使用梯度的二阶矩进行梯度缩放。此时参数更新过程大约是:
\[\begin{aligned} w^{(t+1)} &\leftarrow w^{(t)} -2\alpha \lambda \text{sign}(w^{(t)}) - \alpha \nabla_w L(w) \end{aligned}\]因此对于具有较大梯度的权重,其L2正则化项会被缩小,从而与权重衰减正则化不等价。此时每个元素的惩罚都很均匀,而不是绝对值更大的元素惩罚更大,这部分抵消了L2正则的作用。AdamW算法则将权重衰减从梯度更新过程中解耦,使得所有权重以相同的正则化程度进行衰减:
\[\begin{aligned} w^{(t+1)} &\leftarrow w^{(t)} - \alpha (\frac{\hat{m}^{(t)}(w)}{\sqrt{\hat{v}^{(t)}(w)}+\epsilon}+λ w^{(t)}) \end{aligned}\]⚪ L1正则化 L1 Regularization
L1正则化通过约束参数的L1范数(L1-norm)减小过拟合。带有L1正则化的优化问题可写作:
\[w^*= \mathop{\arg\min}_w \frac{1}{N} \sum_{n=1}^{N} {L(y_n,f(x_n);w)}+λ ||w||_1\]如下图所示,蓝圈为优化函数的等高线,棕色区域为满足L2/L1正则化约束的可行域。当等高线与可行域相交时,L1正则化会优先相交于坐标轴上。故L1正则化会使参数具有稀疏性(sparse)。

(1) 讨论:L1正则化等价于参数服从拉普拉斯分布的最大后验估计
从贝叶斯角度出发,把参数$w$看作随机变量,假设其先验概率$p(w)$服从拉普拉斯分布:
\[w \sim L(0,σ_0^2) = \frac{1}{2σ_0^2} \exp(-\frac{|w|}{σ_0^2})\]由贝叶斯定理可得参数$w$的后验概率$p(w|x,y)$:
\[p(w |x, y) = \frac{p(x,y | w)p(w)}{p(y)} \propto p(x,y | w)p(w)\]参数$w$的最大后验估计为:
\[\begin{aligned} \hat{w} &= \mathop{\arg \max}_{w}\log p(w |x, y) = \mathop{\arg \max}_{w}\log p(x,y | w)p(w) \\ &= \mathop{\arg \max}_{w} \log p(x,y | w) +\log \frac{1}{2σ_0^2} \exp(-\frac{|w|}{σ_0^2}) \\ &\propto \mathop{\arg \max}_{w} \log p(x,y | w)-\frac{|w|}{σ_0^2} \\ &= \mathop{\arg \min}_{w} \log p(x,y | w)+\frac{1}{σ_0^2}||w||_1 \end{aligned}\]因此参数服从拉普拉斯分布的最大后验估计等价于引入L1正则化。
⚪ 弹性网络正则化 Elastic Net Regularization
弹性网络正则化 (Elastic Net Regularization)是指同时约束参数的L2范数和L1范数:
\[w^*= \mathop{\arg\min}_w \frac{1}{N} \sum_{n=1}^{N} {L(y_n,f(x_n);w)}+λ_2 ||w||_2^2+λ_1 ||w||_1\]⚪ L0正则化 L0 Regularization
L0正则化是指约束参数的L0范数(不为零的参数数量):
\[\begin{aligned} w^*&= \mathop{\arg\min}_w \frac{1}{N} \sum_{n=1}^{N} {L(y_n,f(x_n);w)}+λ_0 ||w||_0 \\ ||w||_0 &= \sum_{j=1}^{|w|} \mathbb{I}[w_j \neq 0] \end{aligned}\]上述损失项不可微,可通过hard concrete分布对其进行重参数化:
\[\begin{aligned} w^*&= \mathop{\arg\min}_w \frac{1}{N} \sum_{n=1}^{N} {L(y_n,f(x_n);w \odot z)}+λ_0 \sum_{j=1}^{|w|} \text{sigmoid}(\log \alpha_j - \beta \log \frac{-\gamma}{\zeta}) \\ u & \sim U[0,1] \\ s &= \text{sigmoid}((\log u - \log(1-u) + \log \alpha)/\beta) \\ \overline{s} &= s(\zeta - \gamma) + \gamma \\ z &= \min(1, \max(0, \overline{s})) \end{aligned}\]⚪ 谱正则化 Spectral Norm Regularization
谱正则化 (Spectral Norm Regularization)是指把谱范数(spectral norm)的平方作为正则项,从而增强网络的泛化性:
\[\mathcal{L}(x,y;W) + \lambda ||W||_2^2\]谱正则化使网络更好地满足Lipschitz连续性。Lipschitz连续性保证了函数对于输入扰动的稳定性,即函数的输出变化相对输入变化是缓慢的。
谱范数是一种由向量范数诱导出来的矩阵范数,作用相当于向量的模长:
\[||W||_2 = \mathop{\max}_{x \neq 0} \frac{||Wx||}{||x||}\]谱范数$||W||_2$的平方的取值为$W^TW$的最大特征值。
⚪ 自正交性正则化 Self-Orthogonality Regularization
自正交性正则化不仅能促进模型参数的正交性,而且能带来一定的结果提升。给定两个参数向量$w_i,w_j$,$\theta_{i,j} \in [0, \pi]$是它们的夹角,\(x\)是对应的输入向量,则有:
\[\mathcal{V}_{i,j} = \mathbb{E}_{x \sim \mathcal{X}}\left[ \text{sign}\left(x^Tw_i\right)\text{sign}\left(x^Tw_j\right) \right] = 1 - \frac{2\theta}{\pi}\]若参数向量\(w_i,w_j\)正交,则\(\mathcal{V}_{i,j}=0\)。因此可以构造正则项:
\[\mathcal{R}_{\mathcal{V}} = \lambda_1 \left(\sum_{i \neq j}\mathcal{V}_{i,j}\right)^2 + \lambda_2 \sum_{i \neq j} \mathcal{V}_{i,j}^2\]⚪ WEISSI正则化 Weight-Scale-Shift-Invariance Regularization
基于ReLU族的神经网络通常具有权重尺度偏移不变性 (Weight-Scale-Shift-Invariance,WEISSI)。即对网络参数引入偏移$W_l=\gamma_l\tilde{W}_l$,当\(\prod_{l=1}^L \gamma_l=1\)时网络的输出不变:
\[\begin{aligned} h_L &= f\left(W_Lf\left(W_{L-1}f(\cdots f\left(W_1x\right))\right)\right) \\ &= \left( \prod_{l=1}^L \gamma_l \right) f\left(\tilde{W}_Lf\left(\tilde{W}_{L-1}f\left(\cdots f\left(\tilde{W}_1x\right)\right)\right)\right) \\ \end{aligned}\]而L2正则化项不具有权重尺度偏移不变性:
\[\sum_{l=1}^L || W_l||_2^2 = \sum_{l=1}^L \gamma_l^2|| \tilde{W}_l||_2^2 \neq \sum_{l=1}^L || \tilde{W}_l||_2^2\]此时模型完全可以找到一组新的参数\(\{\tilde{W}_l,\tilde{b}_l\}\),它跟原来参数\(\{W_l,b_l\}\)完全等价(没有提升泛化性能),但是L2正则项更小。
若希望正则项具有尺度偏移不变性,由于优化过程只需要用到正则项的梯度,则应有:
\[\frac{d}{dx} f(\gamma x) = \frac{d}{dx} f( x)\]满足上式的一个解是对数函数$f(x) =\log(x)$。因此对应的正则项为:
\[\mathcal{L}_{reg} = \sum_{l=1}^L \log(||W_l||_2) = \log(\prod_{l=1}^L||W_l||_2)\]⚪ 梯度惩罚 Gradient Penalty
(1)对参数的梯度惩罚
梯度下降算法是一种一阶近似优化算法,相当于隐式地在损失函数中添加了对参数的梯度惩罚项:
\[\begin{aligned} \tilde{g}(W) & \approx g(W) + \frac{1}{4}\gamma \nabla_{W} ||g(W)||^2 \\ & = \nabla_{W} \left( L(W) + \frac{1}{4}\gamma ||\nabla_{W} L(W)||^2 \right) \end{aligned}\]梯度惩罚项有助于模型到达更加平缓的区域,有利于提高泛化性能。此外也可以显式地将梯度惩罚加入到损失中:
\[\mathcal{L}(x,y;W) + \lambda ||\nabla_{W} \mathcal{L}(x,y;W)||^2\](2)对输入的梯度惩罚
在对抗训练中,对输入样本施加\(\epsilon \nabla_x \mathcal{L}(x,y;\theta)\)的对抗扰动,等价于向损失函数中加入对输入的梯度惩罚:
\[\begin{aligned} \mathcal{L}(x+\Delta x,y;W) &\approx \mathcal{L}(x,y;W)+\epsilon ||\nabla_x\mathcal{L}(x,y;W)||^2 \end{aligned}\]此时梯度惩罚(或对抗训练)使得模型对于较小的输入扰动具有鲁棒性。此外,对输入的梯度惩罚也被用于约束模型的Lipschitz连续性。
对输入的梯度惩罚跟Dirichlet能量有关,Dirichlet能量则可以作为模型复杂度的表征。所以施加对输入的梯度惩罚,会倾向于选择复杂度比较小的模型。
(3)两者的关系
对参数的梯度惩罚一定程度上包含了输入的梯度惩罚:
\[\begin{aligned} ||\nabla_x f||^2 \left( \frac{||h^{(l)}||^2}{||W^{(l)}||^2||\nabla_x h^{(l)}||^2} \right) &\leq ||\nabla_{W^{(l)}} f||^2 \\ \end{aligned}\]2. 约束网络结构
⚪ 随机深度 Stochastic Depth
随机深度是指在训练时以一定概率丢弃网络中的模块(令其等价于恒等变换);测试时使用完整的网络,并且按照丢弃概率对各个模块的输出进行加权。

⚪ Dropout
Dropout是指在训练深度神经网络时,随机丢弃一部分神经元。即对某一层设置概率$p$,对该层的每个神经元以概率$p$判断是否要丢弃。此时每个神经元的丢弃概率遵循概率$p$的伯努利(Bernoulli)分布。

训练时激活神经元的平均数量是原来的$1-p$倍;而在测试时所有神经元都被激活,故测试时需将该层神经元的输出乘以$1-p$(被保留的概率)。或者采用Inverted Dropout,即在训练时对某一层按概率$p$随机丢弃神经元之后将该层的输出除以$1-p$;测试时不需再做处理。
def dropout(x, level):
if level < 0. or level >= 1:
raise Exception('Dropout level must be in interval [0, 1].')
retain_prob = 1. - level
sample = np.random.binomial(n=1, p=retain_prob, size=x.shape)
x *= sample
x /= retain_prob
return x
从不同角度理解Dropout:
- 正则化Regularization角度:每一次Dropout相当于为原网络引入噪声,测试时通过平均抵消掉噪声;每次训练不会过度依赖于个别的神经元的输出,增强网络的泛化能力;
- 集成Ensemble角度:每一次Dropout相当于从原网络中生成一个子网络,每次迭代相当于训练一个不同的子网络;最终的网络可以看作这些子网络的集成;
- 贝叶斯Bayesian角度:贝叶斯学习假设参数$w$为随机变量,先验分布为$q(w)$,贝叶斯方法的预测结果如下。其中不等号由Monte Carlo方法得到,$w_m$是第$m$次Dropout的网络参数,看作对全部参数$w$的一次采样。
与Dropout相关的工作包括:
| Dropout方法 | 说明 | 示意图 |
|---|---|---|
| Gaussian Dropout | 每个神经元的丢弃概率遵循概率$p$的高斯分布$N(1,p(1-p))$ |  |
| Standout (NeurIPS2013) |
神经元的丢弃概率$p$通过信念网络建模 |  |
| Spatial Dropout (arXiv1411) |
对卷积特征图的通道维度应用Dropout |  |
| DropBlock (arXiv1810) |
随机丢弃图像特征中的一个连续区域 | 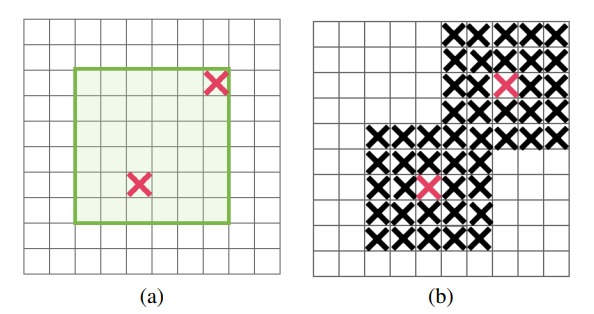 |
| Weighted Channel Dropout (AAAI2019) |
根据激活的相对幅度来选择通道 | 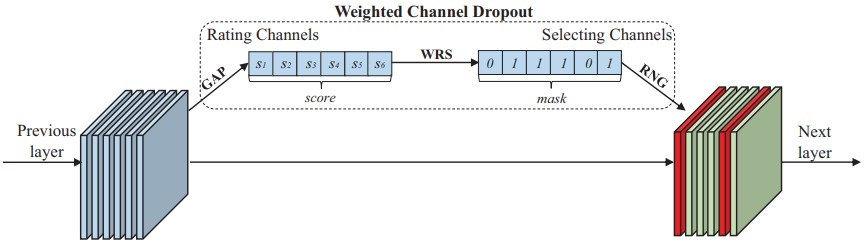 |
| Max-Pooling Dropout (arXiv1512) |
把Dropout应用到最大池化层 |  |
| Max-Drop (ACCV2016) |
把Gaussian Dropout应用到最大池化层 |  |
| MaxDropout (arXiv2007) |
对输入特征进行归一化,然后把大于给定阈值$p$的特征位置设置为$0$ |  |
| R-Drop (arXiv2106) |
通过两次Dropout从同一个模型中获取同一个输入样本的两个不同输出向量,使得两次输出的分布足够接近 |  |
3. 约束优化过程
⚪ 数据增强 Data Augmentation
数据增强(data augmentation)是指通过对样本集中的样本进行额外的操作(通常是加入随机噪声),增加样本集的数据量,提高训练模型的鲁棒性,减少过拟合的风险。
⚪ 梯度裁剪 Gradient Clipping
梯度裁剪用来防止梯度爆炸问题,尤其是在训练深度神经网络时。这种情况常发生在梯度的范数(即大小)变得非常大,导致权重更新过大,从而使得网络训练不稳定。
论文Why gradient clipping accelerates training: A theoretical justification for adaptivity指出,梯度裁剪相当于为模型引入$(L_0,L_1)$-Smooth约束:
\[||\nabla_{\theta}f(\theta+\Delta \theta) - \nabla_{\theta}f(\theta)|| \leq \left(L_0+L_1 ||\nabla_{\theta}f(\theta)||\right) ||\Delta \theta||\]梯度裁剪有两种实现方式:
(1)数值裁剪 clip_grad_value
直接将每个梯度值裁剪到给定的范围内:
\[\theta \leftarrow \theta - \eta \text{Clip} \left( \nabla_{\theta}f(\theta) , - \text{maxVal}, \text{maxVal} \right)\]losses.backward()
torch.nn.utils.clip_grad_value_(
model.parameters(),
clip_value,
foreach=None, # 使用更快的基于 foreach 的实现
)
optimizer.step()
(2)范数裁剪 clip_grad_norm
通过将梯度的范数裁剪到一个最大值 maxNorm 来控制梯度大小。首先计算所有参数的梯度的L2范数:
\[\text{totalNorm} = \sqrt{\sum_i ||\text{grad}_i||_2^2}\]如果 totalNorm 小于等于 maxNorm,则不需要裁剪,梯度保持不变;如果 totalNorm 大于 maxNorm,则按比例将所有梯度缩放,以使新梯度的整体范数等于 maxNorm:
\[\text{grad}_i = \text{grad}_i \times \min\left(1, \frac{\text{maxNorm}}{\text{totalNorm}}\right)\]losses.backward()
torch.nn.utils.clip_grad_norm_(
model.parameters(),
clip_max_norm,
norm_type=2.0, # 所用 p 范数的类型
error_if_nonfinite=False, # 梯度的总范数为nan,inf时是否抛出错误
foreach=None, # 使用更快的基于 foreach 的实现
)
optimizer.step()
⚪ Early Stopping
Early Stop是指训练时当观察到验证集上的错误不再下降,就停止迭代。具体停止迭代的时机,可参考Early stopping-but when?。

⚪ 标签平滑 Label Smoothing
标签平滑 (Label Smoothing)是指对样本的标签引入一定的噪声。(对于分类任务)样本的标签一般用one-hot向量表示:$y=(0,…,0,1,0,…,0)^T$。这是一种Hard Target,若样本标签本身是错误的,会导致严重的过拟合。
标签平滑技术引入噪声对标签进行平滑,假设样本以$ε$的概率被错误标注为其他类别,则可以把标签修改为一种Soft Target:
\[y'=(\frac{ε}{K-1},...,\frac{ε}{K-1},1-ε,\frac{ε}{K-1},...,\frac{ε}{K-1})^T\]⚪ 变分信息瓶颈 Variational Information Bottleneck
深度学习模型可以被拆分成编码+预测两个步骤。第一步是把$x$编码为一个隐变量$z$,第二步是把隐变量$z$预测为标签$y$。
变分信息瓶颈希望能尽可能地减少隐变量$z$包含的信息量,在实现时为损失函数引入互信息$I(x,z)$的变分上界。对于分类任务,引入变分信息瓶颈后的总损失函数表示为:
\[\begin{aligned} \mathcal{L} &= \mathbb{E}_{p(x)} \left[ \mathbb{E}_{p(z|x)} \left[ -\log p(y|z) \right] + \lambda KL\left[ p(z|x) \mid\mid q(z)\right] \right] \\ \end{aligned}\]相比原始的监督学习任务,变分信息瓶颈的改动是:
- 使用编码器$p(z|x)$编码特征的均值和方差,加入了重参数化操作;
- 加入了后验分布$p(z|x)$与给定的先验分布$q(z)$之间的KL散度为额外的损失函数。
⚪ 虚拟对抗训练 Virtual Adversarial Training
- paper:Virtual Adversarial Training: A Regularization Method for Supervised and Semi-Supervised Learning
虚拟对抗训练通过寻找使得损失$l(f(x+\epsilon),f(x))$尽可能大的扰动噪声$\epsilon$,并最小化该损失,从而增强网络对于扰动噪声的鲁棒性。
VAT的完整流程如下:
- 初始化向量\(u\sim \mathcal{N}(0,1)\)、标量$\epsilon, \xi$;
- 迭代$r$次:\(\begin{aligned} u &\leftarrow \frac{u}{\mid\mid u \mid\mid} \\ u &\leftarrow \nabla_x l(f(x+\xi u),f_{sg}(x)) \end{aligned}\)
- $u \leftarrow \frac{u}{\mid\mid u \mid\mid}$
- 用$l(f(x+\epsilon u),f_{sg}(x))$作为损失函数执行梯度下降。
⚪ Flooding
过参数化的深度网络能够在训练后实现零训练误差,此时会记忆训练数据,尽管训练损失接近0,但测试精度下降。flooding正则化方法为损失函数指定一个合理的较小值$b$,使其在优化时在该值附近波动,而不至于损失下降过小。此时尽管训练损失不会下降,但测试损失会进一步下降,从而具有更好的泛化性。
\[\tilde{\mathcal{L}}(w) = | \mathcal{L}(w) -b| + b\]

