1. 权重尺度偏移 Weight Scale Shift

常见的深度学习模型中往往存在“权重尺度偏移（Weight Scale Shift）”现象，这个现象可能会导致L2正则化的作用没那么明显。

深度学习模型的基本结构是“线性变换+非线性激活函数”，而最常用的激活函数之一是$ReLU(x)=\max(x,0)$。该函数具有“正齐次性”，也就是对于$ε≥0$，有$εf(x)=f(εx)$恒成立。

“正齐次性”使得深度学习模型对于权重尺度偏移具有一定的不变性。具体来说，假设一个$L$层的模型：

\[\begin{aligned} h_L &= f\left(W_Lh_{L-1}+b_L\right) \\ &= f\left(W_Lf\left(W_{L-1}h_{L-2}+b_{L-1}\right)+b_L\right) \\ & = \cdots \\ &= f\left(W_Lf\left(W_{L-1}f(\cdots f\left(W_1x+b_1\right)\cdots)+b_{L-1}\right)+b_L\right) \\ \end{aligned}\]

假设为每个参数引入偏移$W_l=\gamma_l\tilde{W}_l,b_l=\gamma_l\tilde{b}_l$，根据正齐次性可得：

\[\begin{aligned} h_L &= \left( \prod_{l=1}^L \gamma_l \right) f\left(\tilde{W}_Lh_{L-1}+\tilde{b}_L\right) \\ & = \cdots \\ &= \left( \prod_{l=1}^L \gamma_l \right) f\left(\tilde{W}_Lf\left(\tilde{W}_{L-1}f(\cdots f\left(\tilde{W}_1x+\tilde{b}_1\right)\cdots)+\tilde{b}_{L-1}\right)+\tilde{b}_L\right) \\ \end{aligned}\]

如果$\prod_{l=1}^L \gamma_l=1$，则模型完全等价。此时模型对于$\prod_{l=1}^L \gamma_l=1$的权重尺度偏移具有不变性 (WEIght-Scale-Shift-Invariance，WEISSI)。

2. L2正则化与WEISSI正则化

尽管两组模型参数$\{W_l,b_l\}$和$\{\tilde{W}_l,\tilde{b}_l\}$对于$\prod_{l=1}^L \gamma_l=1$的权重尺度偏移具有不变性，此时两者对应的L2正则化项却可能不等价。

\[\sum_{l=1}^L || W_l||_2^2 = \sum_{l=1}^L \gamma_l^2|| \tilde{W}_l||_2^2 \neq \sum_{l=1}^L || \tilde{W}_l||_2^2\]

这体现了L2正则化的低效性。假如已经训练得到一组参数$\{W_l,b_l\}$，这组参数泛化性不太好，于是引入L2正则帮助优化器找到一组更好参数。但是由于权重尺度偏移不变性的存在，模型完全可以找到一组新的参数$\{\tilde{W}_l,\tilde{b}_l\}$，它跟原来参数的模型完全等价（没有提升泛化性能），但是L2正则项更小。

如果固定$W_l$，并保持约束$\prod_{l=1}^L \gamma_l=1$，则$\sum_{l=1}^L \| \tilde{W}_l\|_2^2$的最小值在：

\[|| \tilde{W}_1||_2=|| \tilde{W}_2||_2=\cdots = || \tilde{W}_L||_2 = \left(\sum_{l=1}^L || W_l||_2\right)^{1/L}\]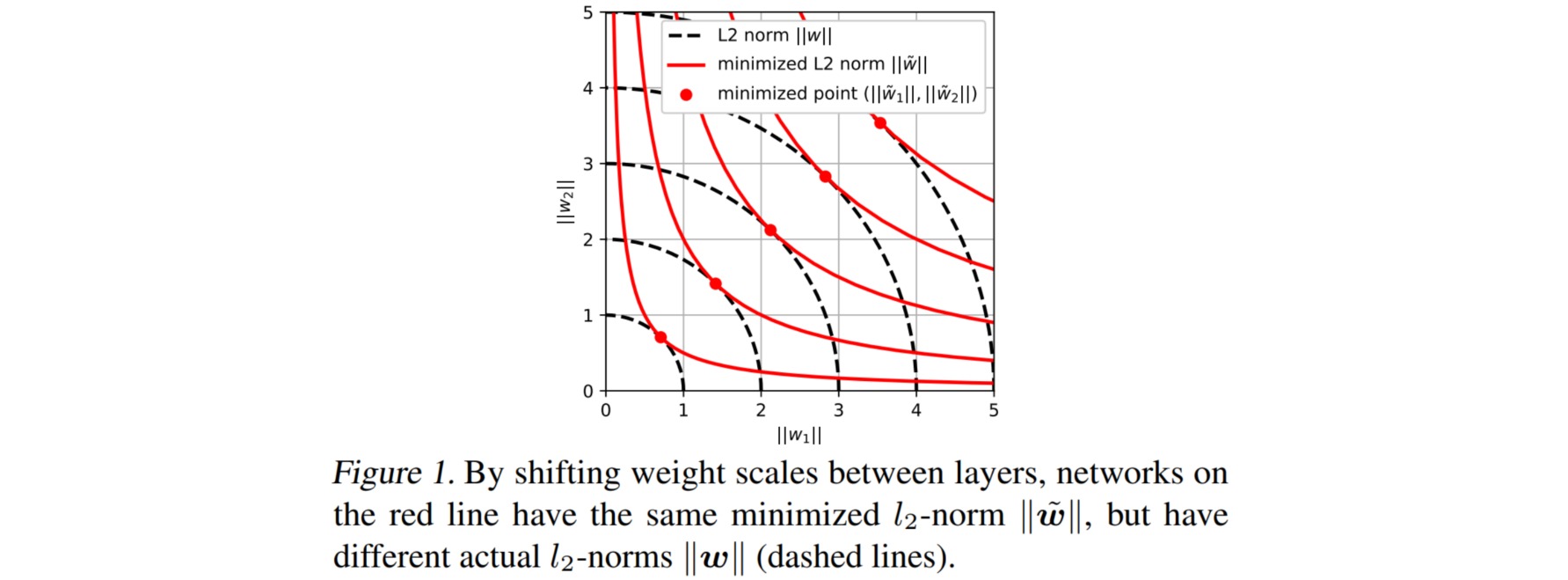

上述问题的根源在于，模型对权重尺度偏移具有不变性，但是L2正则对权重尺度偏移没有不变性。因此希望能找到一个新的正则项，它有类似L2正则的作用，同时还对权重尺度偏移不变。

考虑如下的一般形式的正则项：

\[\mathcal{L}_{reg} = \sum_{l=1}^L f(||W_l||_2)\]

对于L2正则来说，$f(x)=x^2$。只要$f(x)$是关于$x$在$[0,+∞)$上的单调递增函数，那么就能保证优化目标是缩小$||W_l||$。希望正则项具有尺度偏移不变性，由于优化过程只需要用到正则项的梯度，则应有：

\[\frac{d}{dx} f(\gamma x) = \frac{d}{dx} f( x)\]

满足上式的一个解是对数函数$f(x) =\log(x)$。因此对应的正则项为：

\[\mathcal{L}_{reg} = \sum_{l=1}^L \log(||W_l||_2) = \log(\prod_{l=1}^L||W_l||_2)\]

若上述正则项惩罚力度还不够，还可以对参数方向加个L1的惩罚，总的形式为：

\[\mathcal{L}_{reg} = \lambda_1 \sum_{l=1}^L \log(||W_l||_2) + \lambda_2 \sum_{l=1}^L ||\frac{W_l}{||W_l||_2}||_1\]