对抗训练(Adversarial Training)：攻击和防御

Adversarial Training: Attack and Defense.

对抗训练(Adversarial Training)是指通过构造对抗样本，对模型进行对抗攻击和防御来增强模型的稳健性。对抗样本通常是指具有小扰动的样本，对于人类来说“看起来”几乎一样，但对于模型来说预测结果却完全不一样：

对抗攻击是指想办法造出更多的对抗样本；对抗防御是指想办法让模型能正确识别更多的对抗样本；对抗训练是指构造一些对抗样本加入到原数据集中，希望增强模型对对抗样本的鲁棒性。

论文Towards Deep Learning Models Resistant to Adversarial Attacks提出了对抗训练的一般形式：

\[\mathcal{\min}_{\theta} \mathbb{E}_{(x,y)\sim \mathcal{D}} \left[ \mathcal{\max}_{\Delta x \in \Omega} \mathcal{L}(x+\Delta x,y;\theta) \right]\]

其中$\mathcal{D}$表示训练集，$x$表示输入样本，$y$表示样本标签，$\theta$表示模型参数，$\mathcal{L}$是损失函数，$\Delta x$是样本的对抗扰动，$\Omega$是扰动空间。

完整的对抗训练步骤如下：

为输入样本$x$添加对抗扰动$\Delta x$，$\Delta x$的目标是使得损失$\mathcal{L}(x+\Delta x,y;\theta)$尽可能增大，即尽可能让现有模型的预测出错；
对抗扰动$\Delta x$要满足一定的约束，比如模长不超过一个常数$\epsilon$：$\|\Delta x\| \leq \epsilon$；
对每个样本$x$都构造一个对抗样本$x+\Delta x$，用样本对$(x+\Delta x,y)$最小化损失函数训练模型参数$\theta$。

⚪ 讨论：对抗扰动$\Delta x$的约束

在对抗训练中，通常期望为输入样本$x$添加的对抗扰动$\Delta x$是微小的：

\[d(x+\Delta x,x) ≤ ε\]

其中Constraint函数$d(\cdot,\cdot)$可以选用：

L2范数：计算差值图像每个像素的平方和：$d(x,x')=\mid\mid x-x' \mid\mid_2$；寻找满足$d(x+\Delta x,x) ≤ ε$且与原$x$最接近的$x$。
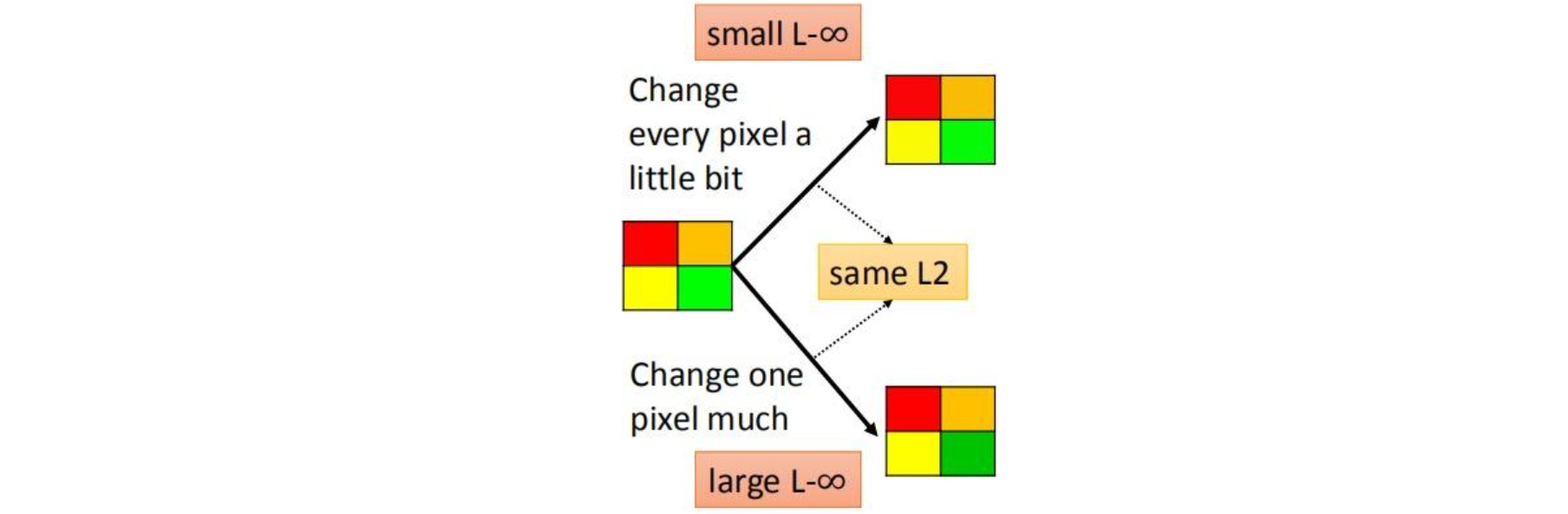
L-∞范数：计算差值图像绝对值最大的像素：$d(x,x')=\mid\mid x-x' \mid\mid_∞$；把$x$超过$ε$的元素限制到$ε$。

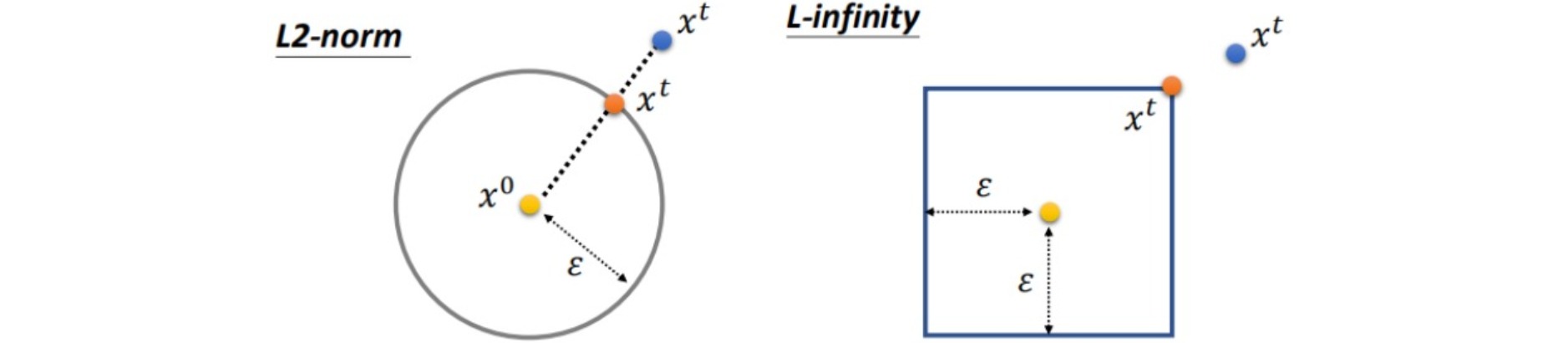
在实践中，L-∞范数约束的使用频率更高，该约束不允许某个像素值的变化特别大：

⚪ 讨论：对抗训练与梯度惩罚

paper：Improving the Adversarial Robustness and Interpretability of Deep Neural Networks by Regularizing their Input Gradients

考虑$\mathcal{L}(x+\Delta x,y;\theta)$对$\Delta x$的泰勒展开：

\[\mathcal{L}(x+\Delta x,y;\theta) \approx \mathcal{L}(x,y;\theta)+<\nabla_x\mathcal{L}(x,y;\theta),\Delta x>\]

对于对抗扰动$\Delta x$，通常选择损失函数的梯度上升方向$\Delta x = \epsilon \nabla_x \mathcal{L}(x,y;\theta)$，代入得：

\[\begin{aligned} \mathcal{L}(x+\Delta x,y;\theta) &\approx \mathcal{L}(x,y;\theta)+<\nabla_x\mathcal{L}(x,y;\theta),\epsilon \nabla_x \mathcal{L}(x,y;\theta)> \\ & = \mathcal{L}(x,y;\theta)+\epsilon ||\nabla_x\mathcal{L}(x,y;\theta)||^2 \end{aligned}\]

因此对输入样本施加$\epsilon \nabla_x \mathcal{L}(x,y;\theta)$的对抗扰动，等价于向损失函数中加入对输入的梯度惩罚。

1. 对抗攻击

对于一个已训练好的模型$f_θ$，输入样本$x$会得到正确的预测结果$y^{true}$，对抗攻击旨在为每个输入样本$x$生成微小的对抗扰动$\Delta x$，使得$x’ = x+\Delta x$输入网络后将不能得到正确的结果$y^{true}$，甚至得到指定的错误结果$y^{false}$。

对抗攻击要求具有跨模型可转移性（cross-model transferability），即对一个模型制作的对抗样本在很大概率下会欺骗其他模型。可转移性使得对抗攻击能够应用于实际，并引发严重的安全问题（自动驾驶、医疗）。

对抗攻击的分类方法：

按照模型参数是否已知：
1. 白盒攻击（white-box attacks）：在已经获取机器学习模型内部的所有信息和参数上进行攻击。已知给定模型的梯度信息生成对抗样本。
2. 黑盒攻击（black-box attacks）：在神经网络结构为黑箱时，仅通过模型的输入和输出，生成对抗样本。
按照对抗样本的更新次数：
1. 单步攻击：仅进行一次更新，容易underfit，针对白盒攻击效果差，针对黑盒攻击效果好（转移性强）；
2. 多步攻击：迭代地更新，容易overfit，针对白盒攻击效果好，针对黑盒攻击效果差（转移性差）。
按照预测类别是否给定：
1. 无目标攻击 (Non-targeted Attack)：构造对抗样本时，使使预测结果偏离正确结果$y^{true}$: $\mathcal{\max}_{\Delta x \in \Omega} \mathcal{L}(x+\Delta x,y^{true};\theta)$；
2. 有目标攻击 (Targeted Attack)：构造对抗样本时，使模型把样本预测为给定的错误类别$y^{false}$: $\mathcal{\max}_{\Delta x \in \Omega} \mathcal{L}(x+\Delta x,y^{true};\theta)-\mathcal{L}(x+\Delta x,y^{false};\theta)$。

常用的对抗攻击方法包括：FGSM, I-FGSM, MI-FGSM, NI-FGSM, DIM, TIM, One Pixel Attack, Black-box Attack。

⚪ FGSM（Fast Gradient Sign Method）

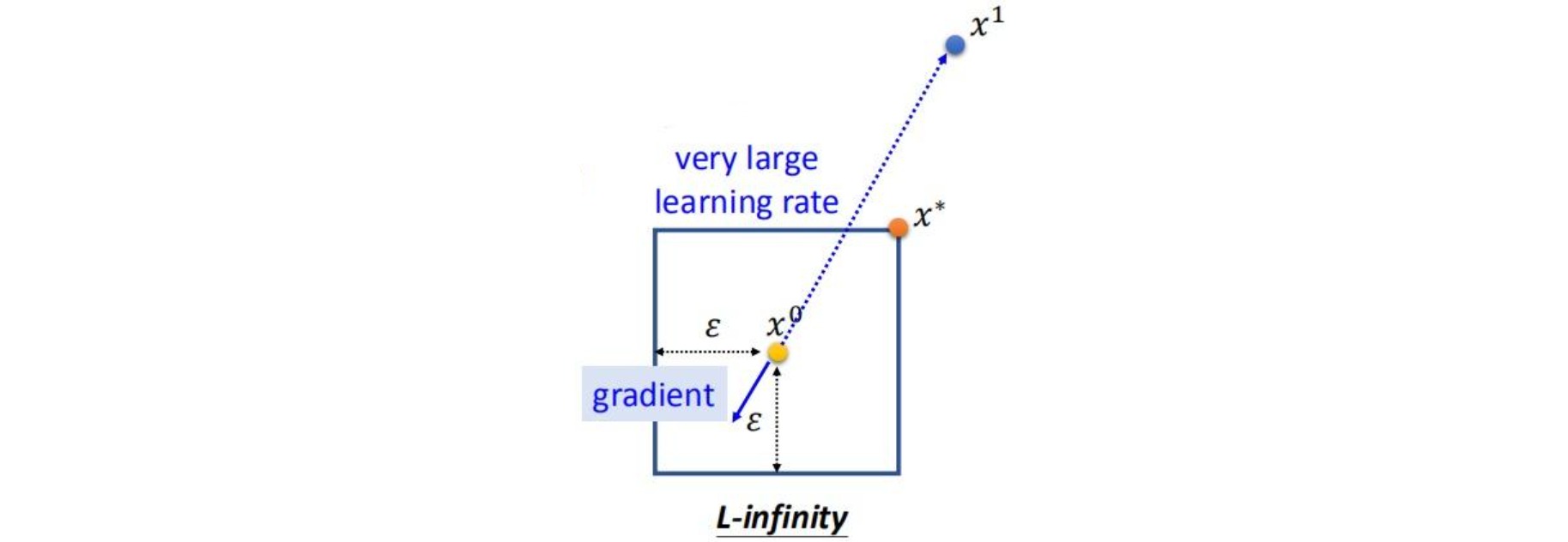
paper：Explaining and Harnessing Adversarial Examples

FGSM通过寻找样本$x$的对抗扰动$\Delta x$来使损失函数$\mathcal{L}(x+\Delta x,y;\theta)$最大化。假设决策边界周围的数据点是线性的，采用梯度上升让损失函数增大，即沿梯度方向移动步长$\epsilon$：

\[\Delta x={\epsilon} \cdot \text{sign}({\nabla}_x\mathcal{L}(x,y;\theta))\]

FGSM方法相当于使用了无穷大的学习率更新样本后，再使用L-∞范数进行约束：

⚪ I-FGSM（Iterative FGSM）

paper：Adversarial examples in the physical world

FGSM算法只涉及单次梯度更新；I-GFSM相比于FGSM，实现迭代更新对抗样本$x^{adv}$，该方法也叫 BIM（Basic Iterative Method）或Projected Gradient Descent（PGD）。如果迭代过程中模长超过了$ϵ$，将溢出的数值用边界值$\epsilon$代替。

\[\begin{aligned} x_0^{adv}&=x \\ x_{t+1}^{adv}&=\text{Clip}_{|x| \leq\epsilon}\{x_{t}^{adv}+{\epsilon} \cdot \text{sign}({\nabla}_x\mathcal{L}(x_{t}^{adv},y;\theta))\} \end{aligned}\]

此外作者还提出了一种有目标的攻击方法：iterative least-likely class method（LLC）：将输入图像分类成原本最不可能分到的类别$y^{LL}$。

\[\begin{aligned} x_0^{adv}&=x \\ x_{t+1}^{adv}&=\text{Clip}_{|x| \leq\epsilon}\{x_{t}^{adv}-{\epsilon} \cdot \text{sign}({\nabla}_x\mathcal{L}(x_{t}^{adv},^{LL};\theta))\} \end{aligned}\]

⚪ MI-FGSM（Momentum Iterative FGSM）

paper：Boosting Adversarial Attacks with Momentum

MI-GFSM在梯度上升中引入了动量方法，稳定更新方向，避免局部极值：

\[\begin{aligned} g_{t+1}&={\mu}g_{t} + \frac{ {\nabla}_x\mathcal{L}(x_{t}^{adv},y;\theta) } {\mid\mid {\nabla}_x\mathcal{L}(x_{t}^{adv},y;\theta) \mid\mid_1} \\ x_{t+1}^{adv}&=\text{Clip}_{|x| \leq\epsilon}\{x_{t}^{adv}+{\epsilon} \cdot \text{sign}(g_{t+1})\} \end{aligned}\]

作者还提出了攻击的集成方法（ensemble attack），即攻击集成模型：

\[l(x) = \sum_{k=1}^{K} w_k l_k(x)\]

其中$w_k$是第$k$个模型对应的权重，$l_k(x)$表示的是第$k$个模型输出的logits。

⚪ NI-FGSM（Nesterov Iterative FGSM）

paper：Nesterov Accelerated Gradient and Scale Invariance for Adversarial Attack

NI-FGSM将Nesterov Accelerated Gradient（NAG）应用到对抗攻击中。相比于Momentum，NAG除了具有稳定梯度更新方向的作用之外，还具有向前看的性质，可以有效加速对抗样本的生成和收敛效果。

\[\begin{aligned} x_t^{nes} &= x_{t}^{adv} + \epsilon \cdot \mu \cdot g_{t} \\ g_{t+1}&={\mu}g_{t} + \frac{ {\nabla}_x\mathcal{L}(x_{t}^{nes},y;\theta) } {\mid\mid {\nabla}_x\mathcal{L}(x_{t}^{nes},y;\theta) \mid\mid_1} \\ x_{t+1}^{adv}&=\text{Clip}_{|x| \leq\epsilon}\{x_{t}^{adv}+{\epsilon} \cdot \text{sign}(g_{t+1})\} \end{aligned}\]

此外，从模型增强的角度出发，通过攻击不同放缩大小的图片，变相实现对被攻击的白盒模型的模型增强，从而提高生成的对抗样本的泛化能力。

⚪ DIM（Diverse Input Method）

paper：Improving Transferability of Adversarial Examples with Input Diversity

DIM对每次攻击图像引入了一个随机移植函数$T$，每轮更新有概率$p$会对图像进行resize和padding操作：

\[\begin{aligned} x_0^{adv}&=x \\ x_{t+1}^{adv}&=\text{Clip}_{|x| \leq\epsilon}\{x_{t}^{adv}+{\epsilon} \cdot \text{sign}({\nabla}_x\mathcal{L}(T(x_{t}^{adv},p),y;\theta))\} \end{aligned}\]

⚪ TIM（Translation-Invariant Method）

paper：Evading Defenses to Transferable Adversarial Examples by Translation-Invariant Attacks

为了生成对白盒模型的识别区域不敏感的对抗样本，TIM采用的方法是用一系列平移后的图像来优化对抗样本：

\[\begin{aligned} x_0^{adv}&=x \\ x_{t+1}^{adv}&=\text{Clip}_{|x| \leq\epsilon}\{x_{t}^{adv}+{\epsilon} \cdot \text{sign}({\nabla}_x\sum_{i,j} w_{ij}\mathcal{L}(T_{ij}(x_{t}^{adv}),y;\theta))\} \end{aligned}\]

其中$T_{ij}(x)$是平移函数（translation operation），将图像$x$在对应维度平移$i$、$j$个像素点，设置$i,j∈\{-k,…,0,…,k\}$，$k$为平移的最大像素值。这样，生成的对抗样本将减弱对被攻击的白盒模型的识别区域的敏感，这能够帮助其转移到其他模型。

对于上述优化算法，需要计算$(2k+1)^2$张图像的梯度。经过推导：

\[{\nabla}_x\sum_{i,j} w_{ij}\mathcal{L}(T_{ij}(x_{t}^{adv}),y;\theta) ≈W * \nabla_x \mathcal{L}(x_{t}^{adv},y;\theta)\]

因此不需要求得所有图像的梯度；而是求未平移图像的梯度，然后对梯度和由权值$w_{ij}$组成的核$W$做卷积。下面是一些核矩阵的选取方法：

uniform kernel：$W_{ij}=\frac{1}{(2k+1)^2}$
linear kernel：$W_{ij}=\frac{\hat{W}_{ij}}{\sum_{i,j}^{} {\hat{W}_{ij}}},\hat{W}_{ij}=(1-\frac{\mid i \mid}{k+1})\cdot(1-\frac{\mid j \mid}{k+1})$
Gaussian kernel：$W_{ij}=\frac{\hat{W}_{ij}}{\sum_{i,j}^{} {\hat{W}_{ij}}},\hat{W}_{ij}=\frac{1}{2\pi σ^2}\exp(-\frac{i^2+j^2}{2σ^2}), σ=\frac{k}{\sqrt{3}}$

⚪ One Pixel Attack

paper：One pixel attack for fooling deep neural networks

One Pixel Attack只修改图像的一个像素值，即：

\[d(x,x') = \mid\mid x-x' \mid\mid_0 = 1\]

其中$L0$范数表示非零元素的个数。对像素值的修改是通过Differential Evolution实现的。

该方法的出发点是对于图像分类任务，尤其是类别很多时，攻击不需要使正确的类别得分大幅度降低，只需要让某个错误类别的得分超过正确类别即可。

⚪ Black-box Attack

paper：Delving into Transferable Adversarial Examples and Black-box Attacks

当模型未知时，如果能获得模型的训练数据，用训练数据自行训练一个proxy network；在proxy network上获得的attack object，通常可以对原模型进行攻击。

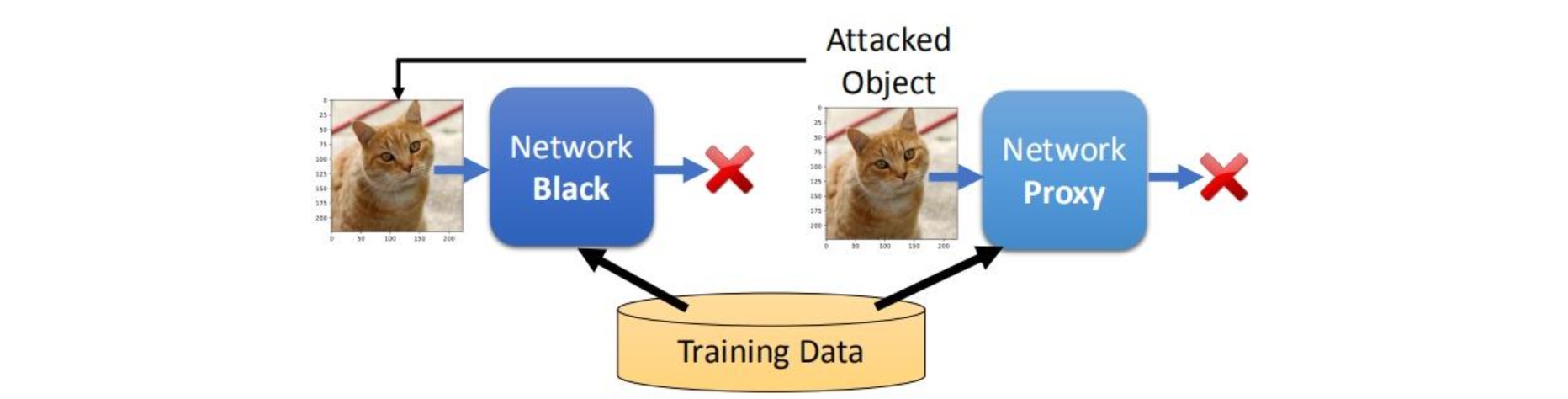
如果没有训练数据，则自己利用原网络构造一些输入-输出对作为训练数据。

2. 对抗防御

Defense可以分为被动式和主动式：

Passive defense：不修改模型，找到异常的图像，类似于异常检测Anomaly Detection。常用方法包括Smoothing, Feature Squeezing, Randomization。
Proactive defense：训练模型，使其对对抗攻击具有鲁棒性。

(1) 被动式防御 Passive defense

⚪ Smoothing

对输入图像进行平滑滤波：

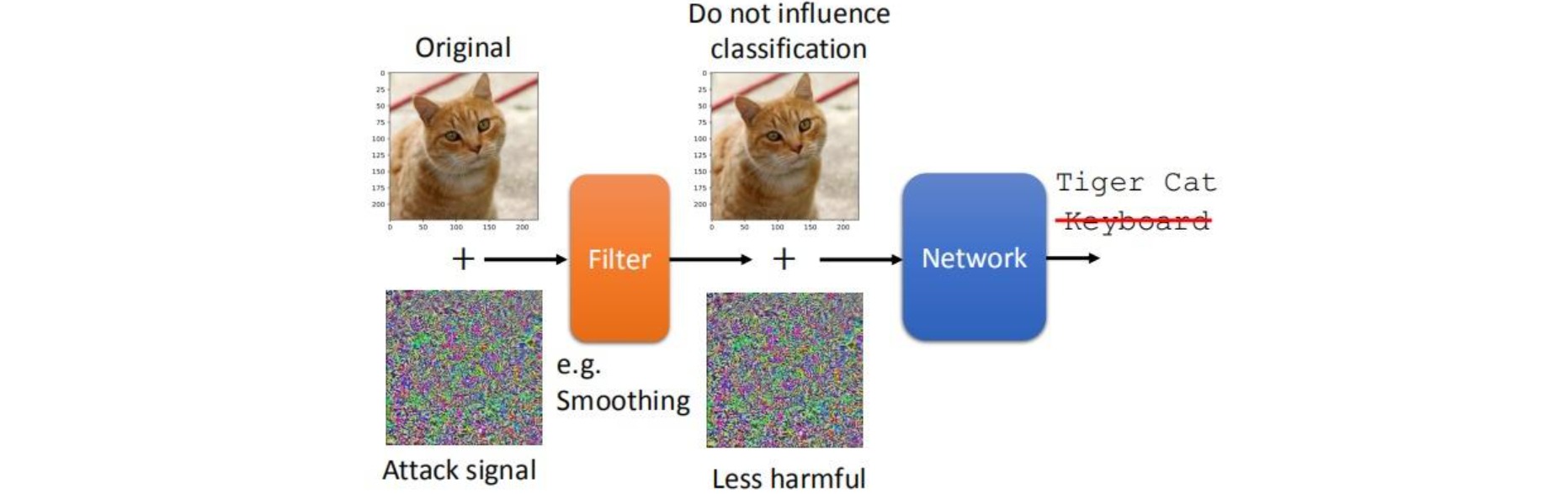
⚪ Feature Squeezing

paper：Feature Squeezing: Detecting Adversarial Examples in Deep Neural Networks

用多个不同的卷积filter进行检测：

⚪ Randomization

paper：Mitigating Adversarial Effects Through Randomization

对输入图像做一些随机的resize和padding：

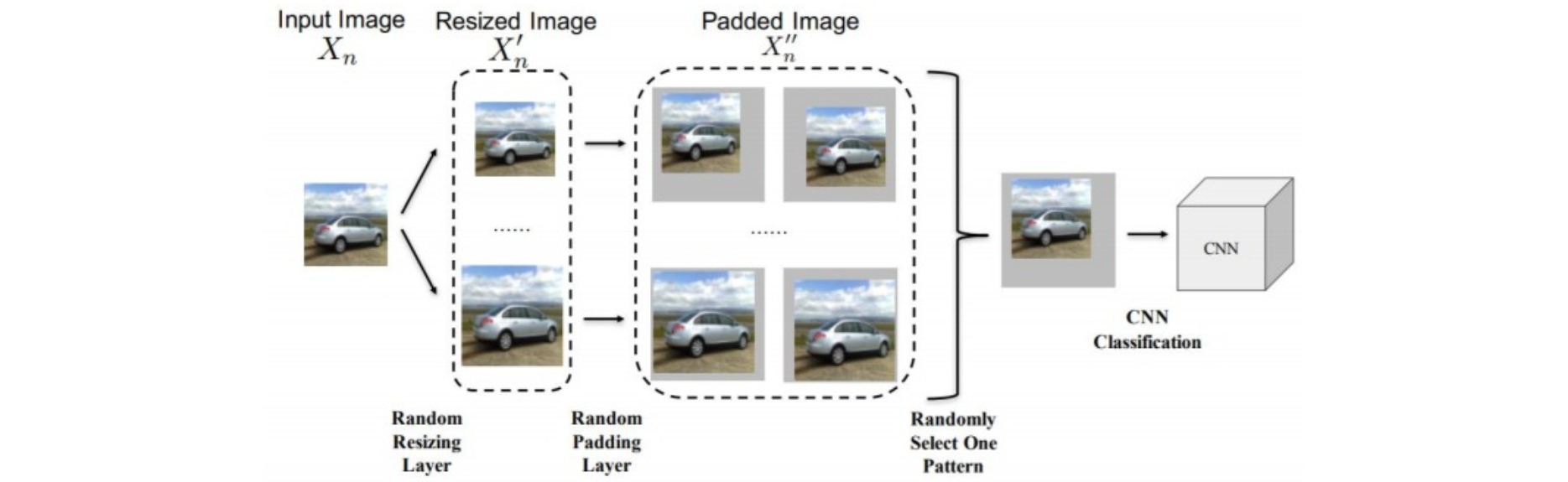
(2) 主动式防御 Proactive defense

给定训练数据$X={(x^1,y^1),...,(x^N,y^N)}$，从$t=1$到$T$进行迭代：每次迭代时对每个样本$x^n$，构造一个对抗攻击的样本$\hat{x}^n$，将其作为新的训练数据；每轮得到新的训练数据$X'={(\hat{x}^1,y^1),...,(\hat{x}^N,y^N)}$，更新模型。

为什么要进行$T$次迭代？：每次使用对抗攻击的样本更新模型时可能会产生新的漏洞。