Normalization in Deep Learning.

输入数据的特征通常具有不同的量纲和取值范围，使得不同特征的尺度（scale）差异很大。不同机器学习模型对数据特征尺度的敏感程度不同。如果一个机器学习算法在数据特征缩放前后不影响其学习和预测，则称该算法具有尺度不变性（scale invariance），表示为$f(\lambda x)=f(x)$。理论上神经网络具有尺度不变性，但是输入特征的不同尺度会增加训练的困难：

  1. 参数初始化困难：当使用具有饱和区的激活函数$a=f(WX)$时，若特征$X$的不同维度尺度不同，对参数$W$的初始化不合适容易使激活函数陷入饱和区，产生vanishing gradient现象。
  2. 梯度下降法的效率下降：如下图所示，左图是数据特征尺度不同的损失函数等高线，右图是数据特征尺度相同的损失函数等高线。由图可以看出，前者计算得到的梯度方向并不是最优的方向，需要迭代很多次才能收敛；后者的梯度方向近似于最优方向，大大提高了训练效率。
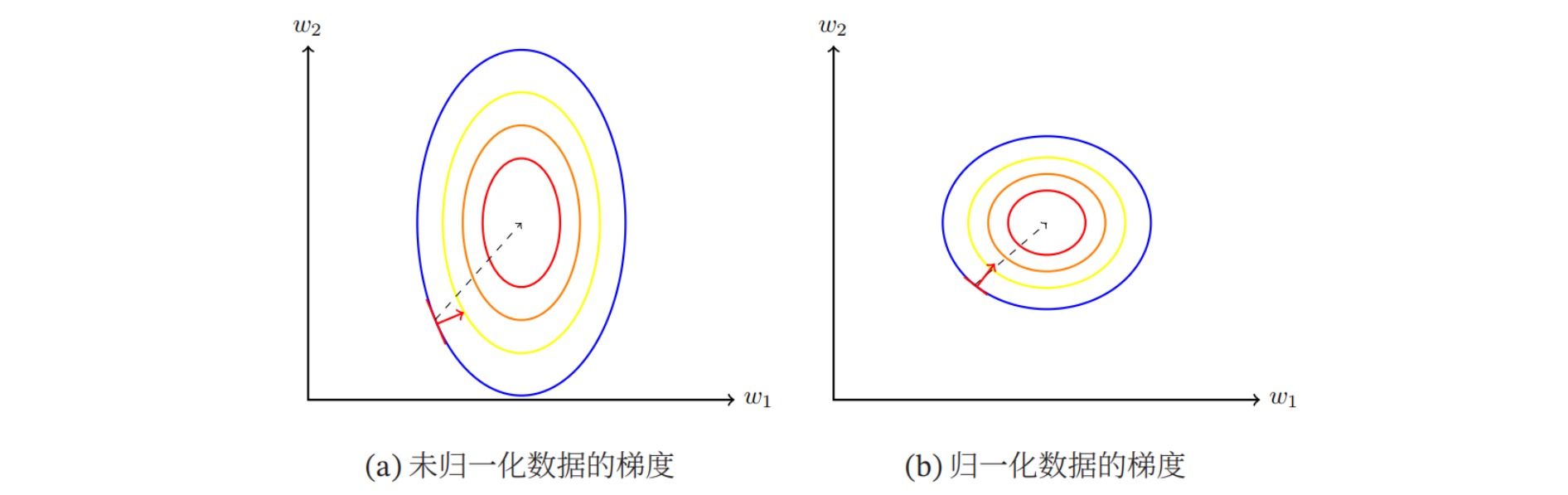
  3. 内部协方差偏移(Internal Covariance Shift)：训练深度网络时，神经网络隐层参数更新会导致网络输出层输出数据的分布发生变化，而且随着层数的增加，这种偏移现象会逐渐被放大。神经网络本质学习的是数据分布，如果数据分布变化了，神经网络又不得不学习新的分布，当前后的要求不同时，可能会影响结果。

归一化（Normalization）泛指把数据特征的不同维度转换到相同尺度的方法。深度学习中常用的归一化方法包括：

  1. 基础归一化方法：最小-最大值归一化、标准化、白化、逐层归一化
  2. 深度学习中的特征归一化：局部响应归一化LRN、批归一化BN、层归一化LN、实例归一化IN、组归一化GN、切换归一化SN
  3. 改进特征归一化：（改进BN）Batch Renormalization, AdaBN, L1-Norm BN, GBN, SPADE；（改进LN）RMS Norm；（改进IN）FRN, AdaIN
  4. 深度学习中的参数归一化：权重归一化WN、余弦归一化CN、谱归一化SN

1. 基础归一化方法

（1）最小-最大值归一化 Min-Max Normalization

最小-最大值归一化是指将每个特征的取值范围归一到$[0,1]$之间。记共有$N$个样本，每个样本含有$D$个特征，其中第$n$个样本表示为$x_n=(x_{n1},…,x_{nD})$；则最小-最大值归一化表示为：

\[x_{nd}\leftarrow \frac{x_{nd}-\min_d(x_{nd})}{\max_d(x_{nd})-\min_d(x_{nd})}\]

（2）标准化 Standardization

标准化又叫Z值归一化（Z-Score Normalization），是指将每个特征调整为均值为0，方差为1：

\[\begin{aligned} μ_d&= \frac{1}{N} \sum_{n=1}^{N} {x_{nd}} \\ σ_d^2&= \frac{1}{N} \sum_{n=1}^{N} {(x_{nd}-μ_d)^2}\\ x_{nd}&\leftarrow \frac{x_{nd}-μ_d}{σ_d} \end{aligned}\]

（3）白化 Whitening

白化在调整特征取值范围的基础上消除了不同特征之间的相关性，降低输入数据特征的冗余。具体地，将输入数据在特征方向上被特征值相除，使数据独立同分布(i.i.d.)，实现输入数据的零均值(zero mean)、单位方差(unit variance)、去相关(decorrelated)。

实现步骤：

  1. 零均值： $ \hat{X}=X-E(X) $
  2. 计算协方差： $ Cov(X)=E(XX^T)-E(X)(E(X))^T $
  3. 去相关： $ Cov(X)^ {-\frac{1}{2}} \hat{X} $

白化的主要缺点是对所有特征一视同仁，可能会放大不重要的特征和噪声；此外，对于深度学习，隐藏层使用白化时反向传播困难。

（4）逐层归一化 Layer-wise Normalizaiton

逐层归一化是指将归一化方法应用于深度神经网络中，对神经网络每一个隐藏层的输入特征都进行归一化，从而提高训练效率。

逐层归一化的优点：

  1. 更好的尺度不变性：通过对每一层的输入进行归一化，不论低层的参数如何变化，高层的输入保持相对稳定，网络具有更好的尺度不变性，可以更高效地进行参数初始化和超参数选择。
  2. 更平滑的损失函数：可以使神经网络的损失函数更平滑，使梯度变得更稳定，可以使用更大的学习率，提高收敛速度。
  3. 隐形的正则化方法：可以提高网络的泛化能力，避免过拟合。

2. 深度学习中的特征归一化

（1）局部响应归一化 Local Response Normalization

局部响应归一化受生物学中“侧抑制”的启发，即活跃的神经元对于相邻的神经元具有抑制的作用。

LRN通常应用在CNN中，且作用于激活函数之后，对邻近的特征映射（表现为邻近的通道）进行归一化。假设一个卷积层的特征图为\(X \in \mathbb{R}^{C×H×W}\)，$H$和$W$是特征图的高度和宽度，$C$为通道数。指定$n$为归一化考虑的邻域通道数量，则LRN表示为：

\[X^c \leftarrow \frac{X^c}{\left(k+\frac{α}{n}\sum_{c'=\max(1,c-\frac{n}{2})}^{\min(C,c+\frac{n}{2})} (X^{c'})^2\right)^β}\]

超参数的取值：$k=1, α=0.0001, β=0.75$。

torch.nn.LocalResponseNorm(size, alpha=0.0001, beta=0.75, k=1.0)

（2）批归一化 Batch Normalization

批归一化（BN）是指对神经网络每一个隐藏层的输入特征使用每一批次数据的统计量进行标准化。BN独立的对每一个特征维度计算统计量，并用mini batch的统计量作为总体统计量的估计（假设每一mini batch和总体数据近似同分布）。对每一个mini batch，计算每个特征维度的均值和（有偏的）方差，并对输入做标准化操作，其中$ε$保证了数值稳定性：

\[y = \frac{x - E[x]}{\sqrt{Var[x]+\epsilon}}*\gamma + \beta\]

注意到当使用具有饱和性质的激活函数（如Sigmoid）时，标准化操作会将几乎所有数据映射到激活函数的非饱和区（线性区），从而降低了神经网络的非线性表达能力。为了保证模型的表达能力不因标准化而下降，引入可学习的rescale和reshift操作$γ,β$。

BN一般应用在网络层（通常是仿射变换）后、激活函数前，此时仿射变换不再需要bias参数（$f(BN(WX+b))=f(BN(WX))$）；测试时，使用总体均值和方差的无偏估计进行标准化（有时也用训练时均值和方差的滑动平均值代替）:

\[\begin{aligned} \overline{\mu} &\leftarrow (1-m)*\overline{\mu}+m*E[x]\\ &+= m*(E[x]-\overline{\mu}) \qquad \text{in-place form} \\ \overline{\sigma}^2 &\leftarrow (1-m)*\overline{\sigma}^2+m*Var[x]\\ &+= m*(Var[x]-\overline{\sigma}^2) \quad \text{in-place form}\\ \end{aligned}\]

BN的作用包括：

  1. 调整每一层输入特征的分布，减缓了vanishing gradient，可以使用更大的学习率;
  2. BN具有权重缩放不变性，减少对参数初始化的敏感程度: $BN((λW)X) = BN(WX)$
  3. 与总体分布差距较小的mini batch分布可以看作为模型训练引入了噪声，可以增加模型的鲁棒性，带有正则化效果；
  4. How Does Batch Normalization Help Optimization?: 对损失函数的landscape增加了平滑约束，从而可以更平稳地进行训练。

BN适用于mini batch比较大、与总体数据分布比较接近的场合。在进行训练之前，要做好充分的shuffle。BN在运行过程中需要计算每个mini batch的统计量，因此不适用于动态的网络结构和RNN网络，也不适合Online Learning（batchsize = 1）。

⚪ BatchNorm1d：应用于MLP

记网络某一层的输入\(X=(x_{nd}) \in \mathbb{R}^{N×D}\)，$N$为batch维度，$D$为该层特征数（神经元个数），则BN表示为：

\[\begin{aligned} μ_d &= \frac{1}{N} \sum_{n=1}^{N} {x_{nd}} \\ σ_d^2&= \frac{1}{N} \sum_{n=1}^{N} {(x_{nd}-μ_d)^2} \\ \hat{x}_{nd}&= \frac{x_{nd}-μ_d}{\sqrt{σ_d^2+\epsilon}} \\ y_{nd} &= γ \hat{x}_{nd} + β \end{aligned}\] 
torch.nn.BatchNorm1d(
    num_features, eps=1e-05,
    momentum=0.1, affine=True,
    track_running_stats=True,
    device=None, dtype=None)

此时BN沿着特征维度$D$进行归一化，沿着批量维度$N$计算统计量因此也被称为时序BN（Temporal Batch Normalization）。

⚪ BatchNorm2d：应用于CNN

记网络某一层的输入\(X=(x_{nchw}) \in \mathbb{R}^{N×C×H×W}\)，$N$为batch维度，$C$为通道维度，$H,W$为空间维度，则BN表示为：

\[\begin{aligned} μ_c&= \frac{1}{NHW} \sum_{n=1}^{N} \sum_{h=1}^{H} {\sum_{w=1}^{W} {x_{nchw}}} \\ σ_c^2&= \frac{1}{NHW} \sum_{n=1}^{N} {\sum_{h=1}^{H} {\sum_{w=1}^{W} {(x_{nchw}-μ_c)^2}}}\\ \hat{x}_{nchw}&= \frac{x_{nchw}-μ_c}{\sqrt{σ_c^2+ε}}\\ y_{nchw} &= γ \hat{x}_{nchw} + β \end{aligned}\] 
torch.nn.BatchNorm2d(
    num_features, eps=1e-05,
    momentum=0.1, affine=True,
    track_running_stats=True,
    device=None, dtype=None)

⚪ BatchNorm2d from sctratch

如果要实现类似 BN 滑动平均的操作，在 forward 函数中要使用原地（inplace）操作给滑动平均赋值。

class BatchNorm2d(nn.Module):
    def __init__(self, dim, eps = 1e-5, momentum=0.1,):
        super(BatchNorm2d, self).__init__()\
        self.dim = dim
        self.eps = eps
        self.m = momentum
        self.gamma = nn.Parameter(torch.ones(1, dim, 1, 1))
        self.beta = nn.Parameter(torch.zeros(1, dim, 1, 1))
        self.register_buffer("running_mean", torch.zeros(dim))
        self.register_buffer("running_var", torch.ones(dim))

    def forward(self, x):
        if self.training:
            mean = x.mean([0, 2, 3])
            var = x.var([0, 2, 3], unbiased=False)
            with torch.no_grad():
                self.running_mean += self.m * (mean - self.running_mean)
                self.running_var += self.m * (var * self.dim/(self.dim-1) - self.running_var) 
        else:
            mean = self.running_mean
            var = self.running_var
        x_norm = (x - mean[None, :, None, None]) / (var[None, :, None, None] + self.eps).sqrt()
        return x_norm * self.gamma + self.beta

（3）层归一化 Layer Normalization

层归一化（LN）适用于序列模型（如RNN,LSTM,Transformer），最初提出是用来解决BN无法应用在RNN网络的问题。

BN沿batch维度计算统计量；而在RNN网络中，每一个样本句子的长度不固定，需要补零来统一长度，此时对于某个特征维度，有些样本可能是无意义的零填充，因此沿batch维度计算统计量是没有意义的。LN针对每一个训练样本计算统计量，即计算每个样本所有特征的均值和方差。

记网络某一层的输入\(X=(x_{nd}) \in \mathbb{R}^{N×D}\)，$N$为batch维度，$D$为该层特征数（神经元个数），则LN表示为：

\[\begin{aligned} μ_n &= \frac{1}{D} \sum_{d=1}^{D} {x_{nd}} \\ σ_n^2&= \frac{1}{D} \sum_{d=1}^{D} {(x_{nd}-μ_n)^2} \\ \hat{x}_{nd}&= \frac{x_{nd}-μ_n}{\sqrt{σ_n^2+\epsilon}} \\ y_{nd} &= γ \hat{x}_{nd} + β \end{aligned}\]

LN也包含可学习的re-scale和re-center参数$\gamma,\beta$，并且参数与单个样本的特征维度相同（作用于每个特征位置）；此外LN不需要在训练过程中动态地保存mini batch的均值和方差，节省了额外的存储空间。

LN的适用场合如下：

  1. LN针对单个训练样本进行，不依赖于其他样本，适用小mini batch、动态网络和RNN，特别是NLP领域；可以Online Learning；
  2. LN对同一个样本的所有特征进行相同的转换，如果不同输入特征含义不同（比如颜色和大小），那么LN的处理可能会降低模型的表达能力；
  3. LN假设同一层的所有channel对结果具有相似的贡献，而CNN中每个通道提取不同模式的特征，因此LN不适用于CNN。
class LayerNorm(nn.Module):
    def __init__(self, normalized_shape, eps = 1e-5):
        super().__init__()
        dim, H, W = normalized_shape
        self.eps = eps
        self.g = nn.Parameter(torch.ones(1, dim, H, W))
        self.b = nn.Parameter(torch.zeros(1, dim, H, W))

    def forward(self, x):
        mean = x.mean([1, 2, 3], keepdim = True)
        var = x.var([1, 2, 3], unbiased = False, keepdim = True)
        return (x - mean) / (var + self.eps).sqrt() * self.g + self.b

torch.nn.LayerNorm(
    normalized_shape, eps=1e-05, # normalized_shape指定计算统计量的维度，如[C,H,W]
    elementwise_affine=True,     # 仿射参数默认作用于每个元素
    device=None, dtype=None
    )

（4）实例归一化 Instance Normalization

实例归一化（IN）适用于生成模型（GAN），最初是在图像风格迁移任务中提出的。

在生成模型中，每一个样本实例之间是独立的，对batch维度计算统计量是不合适的；并且每个图像样本的每个通道之间通常也是独立的。IN计算每个样本在每个通道上的统计量，不仅可以加速模型收敛，并且可以保持每个实例及其通道之间的独立性。

记网络某一层的输入\(X=(x_{nchw}) \in \mathbb{R}^{N×C×H×W}\)，$N$为batch维度，$C$为通道维度，$H,W$为空间维度，则IN表示为：

\[\begin{aligned} μ_{nc}&= \frac{1}{HW} \sum_{h=1}^{H} {\sum_{w=1}^{W} {x_{nchw}}} \\ σ_{nc}^2&= \frac{1}{HW} {\sum_{h=1}^{H} {\sum_{w=1}^{W} {(x_{nchw}-μ_{nc})^2}}}\\ \hat{x}_{nchw}&= \frac{x_{nchw}-μ_{nc}}{\sqrt{σ_{nc}^2+ε}}\\ \end{aligned}\]

IN通常不引入额外的仿射变换。IN应用于CNN时假设每个样本的每个通道是独立的，这可能会忽略部分通道之间的相关性。

class InstanceNorm2d(nn.Module):
    def __init__(self, dim, affine=False, eps = 1e-5):
        super().__init__()
        self.eps = eps
        self.g = nn.Parameter(torch.ones(1, dim, 1, 1))
        self.b = nn.Parameter(torch.zeros(1, dim, 1, 1))

    def forward(self, x):
        mean = x.mean([2, 3], keepdim = True)
        var = x.var([2, 3], unbiased = False, keepdim = True)
        x_norm = (x - mean) / (var + self.eps).sqrt()
        if affine:
            return x_norm * self.g + self.b
        else:
            return x_norm

torch.nn.InstanceNorm2d(
    num_features, eps=1e-05, # normalized_shape指定计算统计量的维度，如[H,W]
    momentum=0.1, affine=False,
    track_running_stats=False,
    device=None, dtype=None
    )

（5）组归一化 Group Normalization

组归一化（GN）是LN和IN的一般形式：LN认为所有通道对输出的贡献是相似的，对每个样本的所有通道一起计算统计量；IN认为每个通道是独立的，对每个样本的每个通道分别计算统计量。

GN将每个样本的通道分成若干组$G$（默认$G=32$），假设组内通道具有相关性、组间通道是独立的，在每组通道内计算统计量。当$G=1$时GN退化为LN，当$G=C$时GN退化为IN。

记网络某一层的输入\(X=(x_{nchw}) \in \mathbb{R}^{N×C×H×W}\)，$N$为batch维度，$C$为通道维度，将$C$分成$G$个组，$H,W$为空间维度，则GN表示为：

\[\begin{aligned} μ_{ng}&= \frac{1}{HWC/G} \sum_{c \in g} \sum_{h=1}^{H} {\sum_{w=1}^{W} {x_{nchw}}} \\ σ_{ng}^2&= \frac{1}{HWC/G} \sum_{c \in g} {\sum_{h=1}^{H} {\sum_{w=1}^{W} {(x_{nchw}-μ_{ng})^2}}}\\ \hat{x}_{nchw}&= \frac{x_{nchw}-μ_{ng}}{\sqrt{σ_{ng}^2+ε}}\\ y_{nchw} &= γ \hat{x}_{nchw} + β \end{aligned}\]

作者通过实验发现GN相比于BN更容易优化，但损失了一定的正则化能力。GN对不同batch size具有很好的鲁棒性，尤其适合batch size较小的计算机视觉任务中（如目标检测，分割）。

torch.nn.GroupNorm(
    num_groups, num_channels,
    eps=1e-05, affine=True,
    device=None, dtype=None
    )

（6）切换归一化 Switchable Normalization

BN、LN、IN分别是minibatch-wise、layer-wise和channel-wise的归一化操作。切换归一化（SN）同时应用这三种方法，学习三种方法的权重，从而适应各种深度学习任务。

如下图所示，不同的深度学习任务具有不同的权重，代表不同归一化方法对不同任务的适合程度。

SN的实现：

\[y_{nchw}=\frac{x_{nchw}-\sum_{k \in Ω}^{} {w_kμ_k}}{\sqrt{\sum_{k \in Ω}^{} {w'_kσ^2_k}+ε}}*γ+β\]

其中$Ω={in,ln,bn}$，注意到三种方法的统计量是相关的，可计算如下：

\[μ_{in}=\frac{1}{HW}\sum_{h,w}^{H,W} {x_{nchw}}， σ^2_{in}=\frac{1}{HW}\sum_{h,w}^{H,W} {(x_{nchw}-μ_{in})^2} \\ μ_{ln}=\frac{1}{C}\sum_{c=1}^{C} {μ_{in}}， σ^2_{ln}=\frac{1}{C}\sum_{c=1}^{C} {(σ^2_{in}+μ^2_{in})}-μ^2_{ln} \\ μ_{bn}=\frac{1}{N}\sum_{n=1}^{N} {μ_{in}}， σ^2_{bn}=\frac{1}{N}\sum_{n=1}^{N} {(σ^2_{in}+μ^2_{in})}-μ^2_{bn}\]

$w_k$和$w_k’$是三种方法对应的权重系数，用参数$λ_{in},λ_{ln},λ_{bn},λ_{in}’,λ_{ln}’,λ_{bn}’$控制：

\[w_k=\frac{e^{λ_k}}{\sum_{z \in Ω}^{} {e^{λ_z}}},\quad w'_k=\frac{e^{λ'_k}}{\sum_{z \in Ω}^{} {e^{λ'_z}}}\]

3. 改进特征归一化

（1）改进Batch Norm

⚪ Synchronized-BatchNorm (SyncBN)

当使用torch.nn.DataParallel将代码运行在多张 GPU 卡上时，PyTorch 的 BN 层默认操作是各卡上数据独立地计算均值和标准差。同步BN (SyncBatchNorm)使用所有卡上的数据一起计算 BN 层的均值和标准差，缓解了当批量大小比较小时对均值和标准差估计不准的情况，是在目标检测等任务中一个有效的提升性能的技巧。

torch.nn.SyncBatchNorm(
    num_features, eps=1e-05,
    momentum=0.1, affine=True,
    track_running_stats=True,
    process_group=None,
    device=None, dtype=None
    )

⚪ Batch Renormalization

BN假设每一mini batch和总体数据近似同分布，用mini batch的统计量作为总体统计量的估计。实际上mini batch和总体的分布存在偏差，Batch Renormalization用一个仿射变换修正这一偏差。

记总体均值为$μ$，方差为$σ^2$；某一mini batch计算的均值为$μ_B$，方差为$σ_B^2$，引入仿射变换：

\[\frac{x-μ}{σ}=\frac{x-μ_B}{σ_B} r+d\]

可以得到一组变换参数为：

\[r=\frac{σ_B}{σ} , d=\frac{μ_B-μ}{σ}\]

当$σ=E(σ_B),μ=E(μ_B)$时，有$E(r)=1,E(d)=0$，这便是BN的假设。注意$r$和$d$是与mini batch有关的常数，并不参与训练，并对上下限进行了裁剪：

\[\begin{aligned} r&=\text{Clip}_{[1/r_{max},r_{max}]}(\frac{σ_B}{σ})\\ d&=\text{Clip}_{[-d_{max},d_{max}]}(\frac{μ_B-μ}{σ}) \end{aligned}\]

在实际使用时，先使用BN（设置$r=1,d=0$）训练得到一个相对稳定的滑动平均，作为总体均值$μ$和方差$σ^2$的近似，再逐渐放松约束。

⚪ Adaptive Batch Normalization (AdaBN)

Domain adaptation (transfer learning)希望能够将在一个训练集上训练的模型应用到一个类似的测试集上。此时训练集和测试集的分布是不同的，应用BN时由训练集得到的统计量不再适合测试集。

AdaBN的思想是用所有测试集数据计算预训练网络每一层的BN统计量（均值和方差），测试时用这些统计量代替由训练得到的原BN统计量:

\[\begin{aligned} μ^l &= \frac{1}{N} \sum_{n=1}^{N} {x^l_{test,n}}\\ σ^l &= \sqrt{\frac{1}{N} \sum_{n=1}^{N} {(x^l_{test,n}-μ^l)^2}+ε} \end{aligned}\]

⚪ L1-Norm Batch Normalization (L1-Norm BN)

BN中存在平方和开根号运算，增加了计算量，需要额外的内存，减慢训练的速度；部署到资源限制的硬件系统（如FPGA）时有困难。

L1-norm BN把BN运算中的L2-norm variance替换成L1-norm variance：

\[σ_B= \frac{1}{N} \sum_{n=1}^{N} {\mid x_n-μ_B \mid}\]

可以证明，（在正态分布假设下）通过L1-norm计算得到的$σ’=E(|X-E(X)|)$和通过L2-norm计算得到的$σ$仅相差一常数：

\[\frac{σ}{E(\mid X-E(X) \mid)}=\sqrt{\frac{\pi}{2}}\]

这个常数可以由rescale时的$γ$参数学习到，所以不显式地引入算法中。

⚪ Generalized Batch Normalization （Generalized BN）

BN使用的是均值和方差统计量，在Generalized BN中使用更一般的统计量$S$和$D$:

\[\hat{x}_n= \frac{x_n-S(x_n)}{D(x_n)}\]

广义偏差测度(Generalized deviation measures)提供了选择$D$和相关统计量$S$的方法。

⚪ Spatially-Adaptive Denormalization (SPADE)

SPADE (Spatially-adaptive denormalization)采用的归一化形式为BatchNorm，即沿着特征的每一个通道维度进行归一化。仿射变换参数$\gamma,\beta$不是标量，而是与空间位置有关的向量$\gamma_{c,x,y},\beta_{c,x,y}$，并由输入语义mask图像通过两层卷积层构造。

向网络中加入SPADE层的参考代码实现如下：

#   SPADE module
class SPADE2d(nn.Module):
    def __init__(self, num_features, eps=1e-5, momentum=0.1):
        super(SPADE2d, self).__init__()
        self.num_features = num_features
        self.eps = eps
        self.momentum = momentum
        # weight and bias are dynamically assigned
        self.weight = None # [1, c, h, w]
        self.bias = None # [1, c, h, w]
        self.bn = nn.BatchNorm2d(
            self.num_features, eps=1e-5,
            momentum=0.1, affine=False,
            )

    def forward(self, x):
        # Apply batch norm
        out = self.bn(out)
        return out*self.weight + self.bias


#            Model
class Model(nn.Module):
    def __init__(self, ):
        super(Model, self).__init__()
        # 定义包含SPADE的主体网络
        self.model = nn.Sequential()
        # 定义生成SPADE参数的网络
        num_spade_params = self.get_num_spade_params()
        self.conv = ConvLayer(input_channel, num_spade_params)

    def get_num_spade_params(self):
        """Return the number of SPADE parameters needed by the model"""
        num_spade_params = 0
        for m in self.modules():
            if m.__class__.__name__ == "SPADE2d":
                num_spade_params += 2 * m.num_features
        return num_spade_params

    def assign_spade_params(self, spade_params):
        """Assign the spade_params to the SPADE layers in model"""
        for m in self.modules():
            if m.__class__.__name__ == "SPADE2d":
                # Extract weight and bias predictions
                m.weight = spade_params[:, : m.num_features, :, :].contiguous()
                m.bias = spade_params[:, m.num_features : 2 * m.num_features, :, :].contiguous()
                # Move pointer
                if spade_params.size(1) > 2*m.num_features:
                    spade_params = spade_params[:, 2*m.num_features:, :, :]

    def forward(self, main_input, cond_input):
        # Update SPADE parameters by ConvLayer prediction based off conditional input
        self.assign_spade_params(self.conv(cond_input))
        out = self.model(main_input)
        return out

（2）改进Layer Norm

⚪ Root Mean Square Layer Normalization (RMSNorm)

RMS Norm去掉了LN中的均值和reshift操作，相当于对每个样本进行了L2归一化，相比于LN减少了计算负担，并且具有相似的效果。

\[\begin{aligned} σ_n^2&= \frac{1}{D} \sum_{d=1}^{D} {x_{nd}^2} \\ \hat{x}_{nd}&= \frac{x_{nd}}{\sqrt{σ_n^2+\epsilon}} \\ y_{nd} &= γ \hat{x}_{nd} \end{aligned}\]

center操作（减均值或reshift操作）类似于全连接层的bias项，储存到的是关于预训练任务的一种先验分布信息；而把这种先验分布信息直接储存在模型中，反而可能会导致模型的迁移能力下降。

（3）改进Instance Norm

⚪ Filter Response Normalization (FRN)

FRN类似于IN，也是对每个样本的每个通道进行的操作。不同于IN，FRN使用二阶矩代替了方差统计量，即计算方差时没有考虑均值。

记网络某一层的输入\(X=(x_{nchw}) \in \mathbb{R}^{N×C×H×W}\)，$N$为batch维度，$C$为通道维度，$H,W$为空间维度，则FRN表示为：

\[\begin{aligned} μ_{nc}&= \frac{1}{HW} \sum_{h=1}^{H} {\sum_{w=1}^{W} {x_{nchw}}} \\ v^2&= \frac{1}{HW} {\sum_{h=1}^{H} {\sum_{w=1}^{W} {x_{nchw}^2}}}\\ \hat{x}_{nchw}&= \frac{x_{nchw}-μ_{nc}}{\sqrt{v^2+ε}}\\ y_{nchw} &= γ \hat{x}_{nchw} + β \end{aligned}\]

⚪ Adaptive Instance Normalization (AdaIN)

本文作者指出，IN通过将特征统计量标准化来实现图像风格的标准化，即IN的仿射参数$\gamma,\beta$设置不同的值可以将特征统计信息标准化到不同的分布，从而将输出图像转换到不同的风格。AdaIN可以实现从内容图像$c$到风格图像$s$的风格迁移：

向网络中加入AdaIN层的参考代码实现如下：

#   AdaIN module
class AdaptiveInstanceNorm2d(nn.Module):
    def __init__(self, num_features, eps=1e-5, momentum=1):
        super(AdaptiveInstanceNorm2d, self).__init__()
        self.eps = eps
        self.momentum = momentum
        # weight and bias are dynamically assigned
        self.weight = None # [1, c]
        self.bias = None # [1, c]
        # fixed init
        self.register_buffer("running_mean", torch.zeros(num_features))
        self.register_buffer("running_var", torch.ones(num_features))

    def forward(self, x):
        b, c, h, w = x.size()
        running_mean = self.running_mean.repeat(b)
        running_var = self.running_var.repeat(b)
        # Apply instance norm
        x_reshaped = x.contiguous().view(1, b * c, h, w)
        out = F.batch_norm(
            x_reshaped, running_mean, running_var,
            self.weight, self.bias, True,
            self.momentum, self.eps
        )
        return out

#            Model
class Model(nn.Module):
    def __init__(self, ):
        super(Model, self).__init__()
        # 定义包含AdaIN的主体网络
        self.model = nn.Sequential()
        # 定义生成AdaIN参数的网络
        num_adain_params = self.get_num_adain_params()
        self.conv = nn.Conv2d(input_channel, num_adain_params, 1, 0, 0)

    def get_num_adain_params(self):
        """Return the number of AdaIN parameters needed by the model"""
        num_adain_params = 0
        for m in self.modules():
            if m.__class__.__name__ == "AdaptiveInstanceNorm2d":
                num_adain_params += 2 * m.num_features
        return num_adain_params

    def assign_adain_params(self, adain_params):
        """Assign the adain_params to the AdaIN layers in model"""
        for m in self.modules():
            if m.__class__.__name__ == "AdaptiveInstanceNorm2d":
                # Extract weight and bias predictions
                weight = adain_params[:, : m.num_features]
                bias = adain_params[:, m.num_features : 2 * m.num_features]
                # Update bias and weight
                m.bias = bias.contiguous().view(-1)
                m.weight = weight.contiguous().view(-1)
                # Move pointer
                if adain_params.size(1) > 2 * m.num_features:
                    adain_params = adain_params[:, 2 * m.num_features :]

    def forward(self, main_input, cond_input):
        # Update AdaIN parameters by ConvLayer prediction based off conditional input
        self.assign_adain_params(self.conv(cond_input))
        out = self.model(main_input)
        return out

4. 深度学习中的参数归一化

之前介绍的归一化方法都是针对网络层中的特征进行的操作，也可以把归一化应用到网络权重上。

（1）权重归一化 Weight Normalization

权重归一化（WN）对权重$W$使用长度标量$g$和方向向量$v$进行重参数化：

\[W=g\frac{v}{\mid\mid v \mid\mid}\]

其中$g= \mid\mid W \mid\mid$，向量$v$由反向传播更新。

由于神经网络中权重经常是共享的，因此这种方法计算开销小于对特征进行归一化的方法，且不依赖于mini batch的统计量。

（2）余弦归一化 Cosine Normalization

对数据进行归一化的原因是因为数据经过神经网络的计算后可能变得很大，导致分布的方差爆炸，而这一问题的根源就是采用的计算方式(点积)，向量点积是无界的。

向量点积是衡量两个向量相似度的方法之一。类似的度量方式还有很多。夹角余弦就是其中一个且有确定界。余弦归一化将点积运算替换为计算余弦相似度，将输出控制在$[-1,1]$之间。

\[Norm(W\cdot X) = \frac{W·X}{\mid\mid W \mid\mid · \mid\mid X \mid\mid}\]

（3）谱归一化 Spectral Normalization

谱归一化(Spectral Normalization)是指使用谱范数(spectral norm)对网络参数进行归一化：

\[W \leftarrow \frac{W}{||W||_2^2}\]

谱归一化精确地使网络满足Lipschitz连续性。Lipschitz连续性保证了函数对于输入扰动的稳定性，即函数的输出变化相对输入变化是缓慢的。

谱范数是一种由向量范数诱导出来的矩阵范数，作用相当于向量的模长：

\[||W||_2 = \mathop{\max}_{x \neq 0} \frac{||Wx||}{||x||}\]

谱范数$||W||_2$的平方的取值为$W^TW$的最大特征值。

model = Model()
def add_sn(m):
        for name, layer in m.named_children():
             m.add_module(name, add_sn(layer))
        if isinstance(m, (nn.Conv2d, nn.Linear)):
             return nn.utils.spectral_norm(m)
        else:
             return m
model = add_sn(model)

值得一提的是，谱归一化是对模型的每一层权重都进行的操作，使得网络的每一层都满足Lipschitz约束；这种约束有时太过强硬，通常只希望整个模型满足Lipschitz约束，而不必强求每一层都满足。