AdaMix：参数高效模型微调中的混合调整.

Adapter 是一种参数高效的微调策略，相比于调整模型原有参数，直接在下游任务中对于先前模型增加一小部分参数，原有参数不变，只用这一小部分参数来在下游任务上取得最优效果。Adapter 模块的具体结构由两个 FFN 组成，中间隐藏维度可以取到很小来缩减参数需求。

AdaMix将 Adapter 定义为：

\[\mathbb{E}_i(x_s)\equiv w_{i}^{o u t}\cdot G e L U(w_{i}^{i n}\cdot x_s)\]

在此基础上AdaMix提出了 Mixture-of-Adapter，类似于多专家模型 (MoE: Mixture-of-Experts)，即将每一个 Adpater 视作一个专家$E$，加上传统的门控单元$G$，模型的输出可以表示为：

\[h(x_s) = \sum_{i}\mathbb{G}(x_{s})_i \mathbb{E}_{i}(x_{s})\]

专家包含了两个 FFN 层（up 映射和 down 映射），每个不同的 down 和 up 的组合都可以视作一个专家：

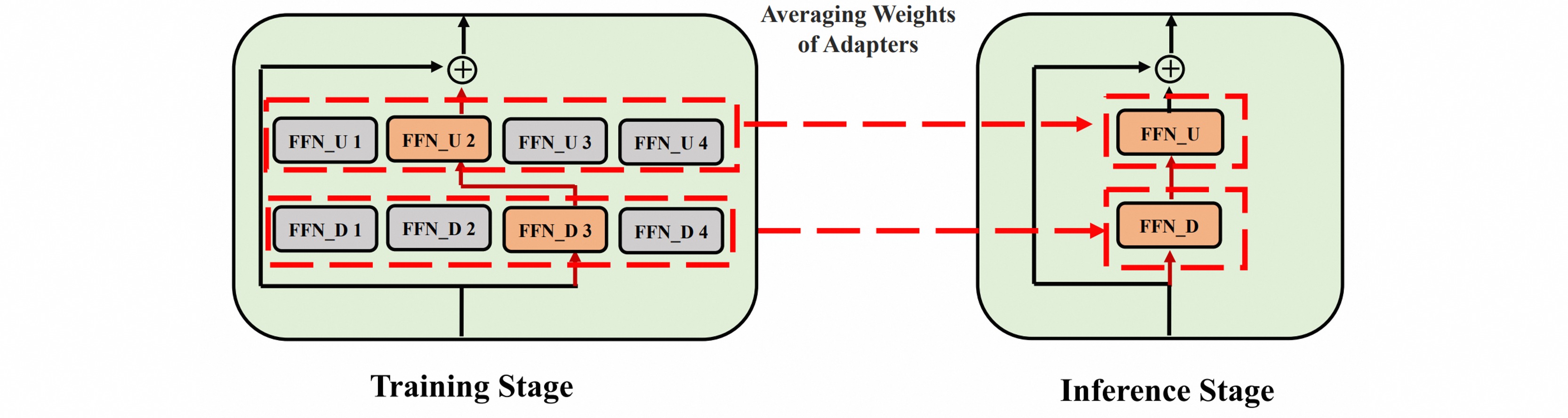
在训练时将门控单元替换为随机平均选择专家的方式，既减少了门控单元所消耗的参数和计算量，又能保证每个专家不会超负荷运作。为了保证随机专家情况下不出现预测不匹配的情况，需要监督两个不同专家的输出一致性。

模型只考虑一个主分支，将最终预测结果做损失；其次为了保证训练高效，在确定了主分支随机选择的专家后，右分支需要满足两个 FFN 专家的选择均与主分支不同。损失函数即为主分支的交叉熵加上两个分支的 KL 一致性损失：

\[\mathcal{L} = -\sum_{c=1}^{C}\left( \mathcal{I}(x,c) \log\operatorname{softmax}(z_{c}^{A}(x))+\frac{1}{2}(\mathcal{KL}(z_{c}^{A}(x))||z_{c}^{B}(x))+\mathcal{KL}(z_{c}^{B}(x)||z_{c}^{A}(x)) \right)\]

对于推理阶段，将所有 Adapter 混合（平均参数），而不是像传统多专家模型中继续沿用门控单元或是随机分配，让参数和计算量达到最小和最高效。

\[\mathcal{W}_{i}^{u p}\leftarrow\frac{1}{M}\sum_{j=1}^{M}\mathcal{W}_{i j}^{u p}\qquad\mathcal{W}_{i}^{d o w n}\leftarrow\frac{1}{M}\sum_{j=1}^{M}\mathcal{W}_{i j}^{d o w n}\] 
class Adamix(nn.Module):
    def __init__(self,
                 d_model,
                 bottleneck,
                 dropout=0.0,
                 init_option="bert",
                 adapter_scalar="1.0",
                 adapter_layernorm_option="in",
                 num_of_adapters=4):
        super().__init__()
        self.n_embd = d_model
        self.down_size = bottleneck
        self.num_of_adapters = num_of_adapters
        #_before
        self.adapter_layernorm_option = adapter_layernorm_option

        self.adapter_layer_norm_before = None
        if adapter_layernorm_option == "in" or adapter_layernorm_option == "out":
            self.adapter_layer_norm_before = nn.LayerNorm(self.n_embd)

        if adapter_scalar == "learnable_scalar":
            self.scale = nn.Parameter(torch.ones(1))
        else:
            self.scale = float(adapter_scalar)

        self.down_projs = nn.ModuleList(nn.Linear(self.n_embd, self.down_size) for _ in range(num_of_adapters))
        self.non_linear_func = nn.ReLU()
        self.up_projs = nn.ModuleList(nn.Linear(self.down_size, self.n_embd) for _ in range(num_of_adapters))

        self.dropout = dropout
        with torch.no_grad():
            for i in range(num_of_adapters):
                nn.init.kaiming_uniform_(self.down_projs[i].weight, a=math.sqrt(5))
                nn.init.zeros_(self.up_projs[i].weight)
                nn.init.zeros_(self.down_projs[i].bias)
                nn.init.zeros_(self.up_projs[i].bias)
    
    def _gengrate_expert_ids(self):
        expert_ids = torch.randint(0, self.num_of_adapters, (2,))
        return expert_ids

    def forward(self, x, add_residual=True, residual=None):
        residual = x if residual is None else residual
        if self.adapter_layernorm_option == 'in':
            x = self.adapter_layer_norm_before(x)
        down_idx, up_idx = self._gengrate_expert_ids()
        down = self.down_projs[down_idx](x)
        down = self.non_linear_func(down)
        down = nn.functional.dropout(down, p=self.dropout, training=self.training)
        up = self.up_projs[up_idx](down)

        up = up * self.scale

        if self.adapter_layernorm_option == 'out':
            up = self.adapter_layer_norm_before(up)

        if add_residual:
            output = up + residual
        else:
            output = up

        return output