Glow:使用1x1可逆卷积构造生成流.
1. 问题建模
流(flow-based)模型旨在对真实数据分布$\hat{p}_X(x)$与隐变量$p_Z(z)$之间的可逆映射关系进行建模。定义生成过程:
\[z~ p_Z(z), x=g(z)\]$g(z)$是可逆的双射函数。给定一个数据样本$x$,隐变量推断由$z=f(x)=g^{−1}(x)$完成。函数$f(x)$由一系列变换复合而成$f=f_1\circ f_2 \circ \cdots \circ f_K$。则变换过程中存在一系列中间特征$h_k=f_k(h_{k-1})$:
\[x = h_0 \leftrightarrow h_1 \leftrightarrow h_2 \leftrightarrow \cdots \leftrightarrow h_{K-1} \leftrightarrow h_K =z\]根据概率密度的变量替换公式,若隐变量的概率分布指定为$p_Z(z)$,则数据分布的概率密度函数$p_X(x)$表示为:
\[p_X(x) = p_Z(z)\cdot |\det[\frac{dz}{dx}]| = p_Z(z)\cdot |\det[\prod_{k=1}^{K}\frac{dh_k}{dh_{k-1}}]|\]目标函数为最大化概率分布的对数似然:
\[\log p_X(x) = \log p_Z(z) +\sum_{k=1}^{K} \log |\det[\frac{dh_k}{dh_{k-1}}]|\]其中$\det [\frac{dh_k}{dh_{k-1}}]$是函数$f_k$在$h_{k-1}$上的Jacobian行列式。为了构造可解的目标函数,要求设计合适的$f$使得Jacobian行列式容易计算。
2. Glow
Glow模型的整体结构受Real NVP启发,采用多尺度结构。

整体模型相当于编码器$z=f(x)$, 原始输入$x$每经过一个flow模块后,输出与$x$尺寸相同的特征,将其沿着通道维度平均分为$z_1,z_2$,其中$z_2$直接输出,而$z_1$作为下一次输入,该过程共进行$L-1$次。最终的输出由$L-1$次中间结果和一次最终结果组成,总大小跟输入一样。在生成$64\times 64$的实验中默认$L=3$。
值得一提的是,模型需要实现推断过程$z=f(x)$用于训练,并且需要同时实现生成过程$x=f^{-1}(z)$用于采样生成结果。
每个flow模块包含一次squeeze操作,一个可逆网络和一次split操作(最后一个输出模块不包含)组成。实验中默认$K=32$。

⚪ squeeze操作
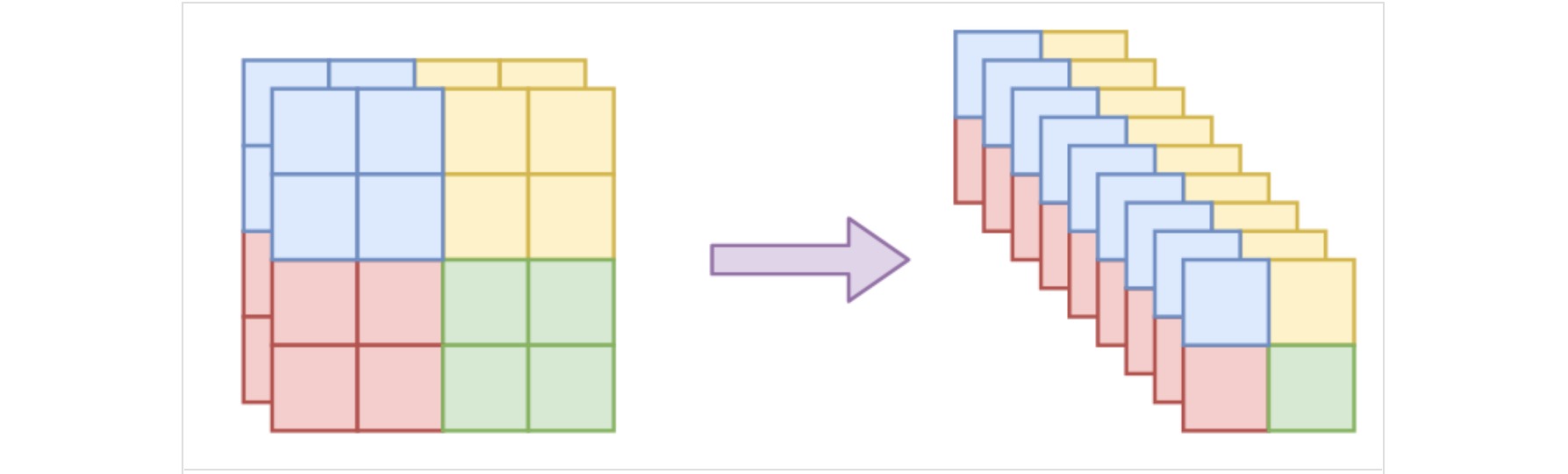
squeeze操作能够增加特征的通道维度,同时保留特征的空间局部相关性。假设输入数据的尺寸为$h×w×c$,沿着空间维度分为一个个$k×k×c$的特征块,然后将每个块调整为$1×1×k^2c$,从而构造$h/k×w/k×k^2c$的特征。
⚪ 可逆网络

可逆网络包含一个actnorm归一化层,一个可逆的$1\times 1$卷积层和一个仿射耦合层。

- actnorm归一化层
actnorm归一化层是对特征的每个元素进行缩放平移变换:
\[\hat{z} = \frac{z-\mu}{\sigma}\]其中$μ,σ$是训练参数,可以用初始batch的均值和方差初始化。
class ActNorm(nn.Module):
def __init__(self, in_channel):
super().__init__()
self.loc = nn.Parameter(torch.zeros(1, in_channel, 1, 1))
self.scale = nn.Parameter(torch.ones(1, in_channel, 1, 1))
self.register_buffer("initialized", torch.tensor(0, dtype=torch.uint8)) # 标记是否为初始batch
def initialize(self, input):
with torch.no_grad():
flatten = input.permute(1, 0, 2, 3).contiguous().view(input.shape[1], -1)
mean = flatten.mean(1).unsqueeze(1).unsqueeze(2).unsqueeze(3).permute(1, 0, 2, 3)
std = flatten.std(1).unsqueeze(1).unsqueeze(2).unsqueeze(3).permute(1, 0, 2, 3)
self.loc.data.copy_(-mean)
self.scale.data.copy_(1 / (std + 1e-6))
def forward(self, input):
_, _, height, width = input.shape
if self.initialized.item() == 0:
self.initialize(input)
self.initialized.fill_(1)
log_abs = logabs(self.scale)
logdet = height * width * torch.sum(log_abs)
return self.scale * (input + self.loc), logdet
def reverse(self, output):
return output / self.scale - self.loc
- 可逆的1x1卷积层
可逆网络中的耦合层会把输入特征沿通道拆分成两部分。为了增强模型的表示能力,可以将通道顺序打乱,使得信息充分混合。常用的打乱方式包括反转或随机打乱,这些操作等价于将一个置换矩阵(单位正交矩阵)作用于数据通道维度,可以通过$1\times 1$卷积层实现(等价于共享权重的、可逆的沿通道维度的全连接层)。
可逆1x1卷积层的思路是将置换矩阵替换成可训练的参数矩阵$W \in \Bbb{R}^{C\times C}$,该变换引入了Jacobian行列式$\det W$。为了保证$W$的可逆性,一般使用“随机正交矩阵”初始化。注意到任意矩阵都有PLU分解:
\[W=PLU\]其中$P$是一个置换矩阵,$L$是一个对角线元素全为$1$的下三角阵,$U$是一个上三角阵。此时Jacobian行列式$\det W = \prod diag(U)$,即$U$的对角线元素的乘积。
在Glow中先随机生成一个正交矩阵,然后做LU分解得到$P,L,U$,固定$P$,约束$L$为对角线元素全为$1$的下三角阵,固定$U$的对角线的正负号,优化$L,U$的其余参数。
from scipy import linalg as la
class InvConv2dLU(nn.Module):
def __init__(self, in_channel):
super().__init__()
weight = np.random.randn(in_channel, in_channel)
q, _ = la.qr(weight)
w_p, w_l, w_u = la.lu(q.astype(np.float32)) # PLU分解
w_s = np.diag(w_u) # 计算U对角线元素
w_u = np.triu(w_u, 1) # 约束U为上三角阵(不包括对角线)
u_mask = np.triu(np.ones_like(w_u), 1) # 全1上三角阵
l_mask = u_mask.T # 全1下三角阵
w_p = torch.from_numpy(w_p)
w_l = torch.from_numpy(w_l)
w_s = torch.from_numpy(w_s)
w_u = torch.from_numpy(w_u)
self.register_buffer("w_p", w_p)
self.register_buffer("u_mask", torch.from_numpy(u_mask))
self.register_buffer("l_mask", torch.from_numpy(l_mask))
self.register_buffer("s_sign", torch.sign(w_s)) # U对角线的正负号
self.register_buffer("l_eye", torch.eye(l_mask.shape[0])) # 单位阵
self.w_l = nn.Parameter(w_l) # 可学习参数:L的下三角元素
self.w_s = nn.Parameter(logabs(w_s)) # 可学习参数:U的对角元素的对数值
self.w_u = nn.Parameter(w_u) # 可学习参数:U的上三角元素
self.weight = (
self.w_p # P为固定值
@ (self.w_l * self.l_mask + self.l_eye) # 下三角阵L对角线元素全为1,其余参数可学习
@ ((self.w_u * self.u_mask) + torch.diag(self.s_sign * torch.exp(self.w_s))) # 上三角阵U对角线的正负号固定,其余参数可学习
)
self.weight = self.weight.unsqueeze(2).unsqueeze(3)
def forward(self, input):
_, _, height, width = input.shape
out = F.conv2d(input, self.weight)
logdet = height * width * torch.sum(self.w_s)
return out, logdet
def reverse(self, output):
return F.conv2d(output, self.weight.squeeze().inverse().unsqueeze(2).unsqueeze(3))
实验结果表明,相比于反转或随机打乱,可逆1x1卷积层能实现更低的损失函数。

- 仿射耦合层
仿射耦合层(Affine Coupling Layer)是Real NVP中设计的一种可逆结构。把$C$个通道的输入变量$x$沿通道拆分成两部分$x_1=x_{1:c}$,$x_2=x_{c+1:C}$,对于输出变量$h$取如下变化:
\[\begin{aligned} h_1&= x_1 \\ h_2&=s(x_1)\otimes x_2+t(x_1) \end{aligned}\]其中$s,t$是任意函数,可以用卷积神经网络实现。该变换的Jacobian矩阵是下三角阵:
\[[\frac{\partial h}{\partial x}] = \begin{pmatrix} I_d & 0 \\ \frac{\partial s}{\partial x_1}\otimes x_2+\frac{\partial t}{\partial x_1} & \text{diag}(s) \end{pmatrix}\]上述Jacobian矩阵的行列式为$s$各元素的乘积$\prod diag(s)$,同时该变换是可逆的:
\[\begin{aligned} x_1&= h_1 \\ x_2&=(h_2-t(h_1))/s(h_1) \end{aligned}\]为了保证可逆性,通常约束$s$各元素均大于$0$。在实现时用神经网络建模输出$\log s$,然后取指数形式$e^{\log s}$。
其中$s,t$设计为如下卷积神经网络:

最后一层使用零初始化,此时初始状态下相当于恒等变换,这有利于训练深层网络。输出增加一次尺度变换。
class AffineCoupling(nn.Module):
def __init__(self, in_channel, filter_size=512):
super().__init__()
# s,t设计的卷积神经网络
self.net = nn.Sequential(
nn.Conv2d(in_channel // 2, filter_size, 3, padding=1),
nn.ReLU(inplace=True),
nn.Conv2d(filter_size, filter_size, 1),
nn.ReLU(inplace=True),
nn.Conv2d(filter_size, in_channel, 3, padding=1),
)
self.net[-1].weight.data.zero_()
self.net[-1].bias.data.zero_()
self.scale = nn.Parameter(torch.zeros(1, in_channel, 1, 1))
def forward(self, input):
in_a, in_b = input.chunk(2, 1)
out_net = self.net(in_a) * torch.exp(self.scale * 3)
log_s, t = out_net.chunk(2, 1)
s = F.sigmoid(log_s + 2)
out_b = (in_b + t) * s
logdet = torch.sum(torch.log(s).view(input.shape[0], -1), 1)
return torch.cat([in_a, out_b], 1), logdet
def reverse(self, output):
out_a, out_b = output.chunk(2, 1)
log_s, t = self.net(out_a).chunk(2, 1)
s = F.sigmoid(log_s + 2)
in_b = out_b / s - t
return torch.cat([out_a, in_b], 1)
值得一提的是,在仿射耦合层中的尺度变换$s(\cdot)$由于actnorm的存在已经不重要了,所以训练大型的模型时,为了节省资源,一般都只用加性耦合层。
⚪ split操作

split操作将每次输出特征$z$拆分成两个$z_1,z_2$,其中$z_2$直接输出,而$z_1$作为下一次输入。此时输出隐变量$z_2$直接取标准正态分布并不合适,因为$z_2$与$z_1$相关,因此有条件分布:
\[p(z_2) = p(z_2|z_1)\]假设$p(z_2|z_1)$为正态分布,其均值和方差通过$z_1$计算(用卷积层回归)。如果仍然构造一个符合标准正态分布的隐变量$\hat{z}_2$,相当于对输出再进行一次变换:
\[\hat{z}_2 = \frac{z_2-\mu(z_1)}{\sigma(z_1)}\]该变换产生行列式$-\sum \log \sigma$。
⚪ 损失函数
Glow的损失函数为负对数似然:
\[loss = - \log p_Z(\hat{z}) -\sum_{k=1}^{K} \log |\det[\frac{dh_k}{dh_{k-1}}]|\]其中隐变量$\hat{z}$的先验分布$p_Z(\hat{z})$预设为各分量独立的标准正态分布:
\[p_Z(\hat{z}) = \frac{1}{(\sqrt{2\pi})^D}e^{-\frac{1}{2}||\hat{z}||^2}\]则损失函数表示为:
\[loss = \frac{1}{2}||\hat{z}||^2 -\sum_{k=1}^{K} \log |\det[\frac{dh_k}{dh_{k-1}}]|\]前者表示输出的平方和,后者表示所有变换贡献的Jacobian行列式$\det[\frac{dh_k}{dh_{k-1}}]$的负对数,来源于actnorm归一化层,可逆$1\times 1$卷积层、仿射耦合层和强制输出隐变量标准化。


