1. 流模型

流(flow-based)模型学习真实数据分布$\hat{p}_X$与隐变量$p_Z$之间可逆、稳定的映射关系。在推断时从数据分布中采样样本$x$，通过函数$f(x)$将其映射为隐空间中的近似样本$z$，隐空间的分布可以人为指定为已知的简单分布形式。在生成时从隐空间分布中采样样本$z$，通过反函数$f^{-1}(x)$将其映射为数据分布中的近似样本$x$。

给定可逆函数$z=f(x)$，根据概率密度的变量替换公式，若隐变量的概率分布指定为$p_Z(z)$，则数据分布的概率密度函数$p_X(x)$表示为：

\[p_X(x) = p_Z(z)\cdot |\det[\frac{\partial f(x)}{\partial x}]|\]

其中$\det [\frac{\partial f(x)}{\partial x}]$是函数$f$在$x$上的Jacobian行列式。通过设计合适的$f$使得Jacobian行列式容易计算。

2. 仿射耦合层

为了使得Jacobian行列式$\det [\frac{\partial f(x)}{\partial x}]$容易计算，并且变换$z=f(x)$的逆变换容易实现，作者设计了一种仿射耦合层(Affine Coupling Layer)。

把$D$维输入变量$x$拆分成两部分$x_1$和$x_2$，对于输出变量$h$取如下变化：

\[\begin{aligned} h_1&= x_1 \\ h_2&=s(x_1)\otimes x_2+t(x_1) \end{aligned}\]

其中$s,t$是任意函数，可以用神经网络实现。该变换的第二个式子相当于对$x_2$的一个仿射变换，故称为仿射耦合层。$x_1$和$x_2$是$x$的某种划分，不失一般性地假设$x_1=x_{1:d}$，$x_2=x_{d+1:D}$，则该变换的Jacobian矩阵是下三角阵：

\[[\frac{\partial h}{\partial x}] = \begin{pmatrix} I_d & 0 \\ \frac{\partial s}{\partial x_1}\otimes x_2+\frac{\partial t}{\partial x_1} & \text{diag}(s) \end{pmatrix}\]

上述Jacobian矩阵的行列式为$s$各元素的乘积，同时该变换是可逆的：

\[\begin{aligned} x_1&= h_1 \\ x_2&=(h_2-t(h_1))/s(h_1) \end{aligned}\]

为了保证可逆性，通常约束$s$各元素均大于$0$。在实现时用神经网络建模输出$\log s$，然后取指数形式$e^{\log s}$。

3. Real NVP

Real NVP全称是实值非体积保持(real-valued non-volume preserving)，这是因为其设计的变换(仿射耦合层)对应的Jacobian行列式不恒等于$1$，而行列式的几何意义为体积变化率，仿射耦合层的行列式不等于$1$就意味着体积有所变化。

⚪ 随机打乱

为了增强模型的表示能力，可以在每个仿射耦合层后随机将向量打乱，使得信息充分混合。随机打乱是指将每一步输出的两个向量$h_1,h_2$拼接成向量$h$，然后将这个向量重新随机排序。

⚪ mask与squeeze操作

为了使得模型适用于处理图像数据，作者在函数$t,m$中引入了卷积层。由于卷积擅长捕捉具有局部相关性的特征，因此在使用仿射耦合层处理数据时也应该设法保留数据的局部相关性。

仿射耦合层将输入数据$x$拆分成两部分$x_1$和$x_2$，经过一系列操作后将输出向量$h$随机打乱。在拆分和打乱的过程中，为了保留输入数据沿空间维度的局部相关性，作者设计了两种分割方法，在实现时是用$0/1$标注原始输入元素，因此也称为mask操作。第一种mask方法是只沿着通道维度进行分割和打乱；第二种mask方法是在空间轴上使用棋盘式的交错分割。

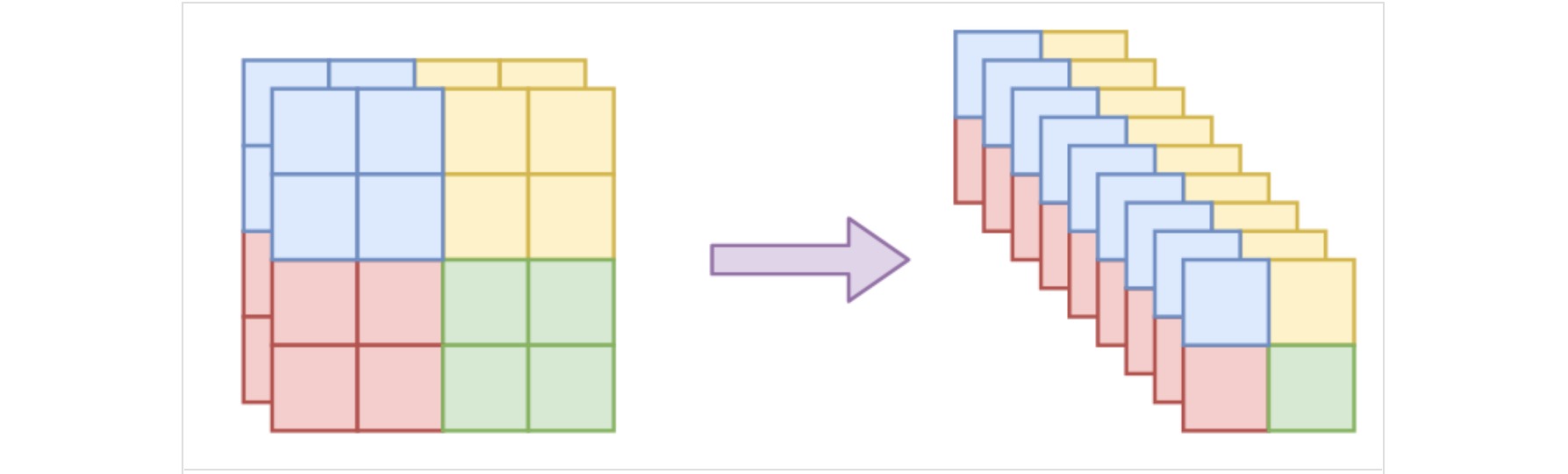
有时输入数据的空间维度远大于通道维度，作者引入squeeze操作构造更多通道维度，同时仍然保留局部相关性。假设输入数据的尺寸为$h×w×c$，沿着空间维度分为一个个$k×k×c$的特征块，然后将每个块调整为$1×1×k^2c$，从而构造$h/k×w/k×k^2c$的特征。

⚪ 多尺度结构

为了进一步提升模型表现，作者引入了多尺度结构。原始输入经过一次flow运算（多个仿射耦合层的复合）后，输出跟输入的大小一样的特征$z$，将其沿着通道维度平均分为$z_1,z_2$，其中$z_1$直接输出，而$z_2$继续进行下一次flow运算，依此类推。最终的输出由多次中间结果$z_1,z_3,z_5$组成，总大小跟输入一样。

多尺度结构能够将每一次flow运算的输入尺寸减半，从而降低计算量，并缓解流模型中隐变量必须与输入尺寸相同造成的维度浪费问题。此时隐变量$z=[z_1,z_3,z_5]$是层次化的，直接取标准正态分布并不合适。注意到$z_1$与$z_2$相关，$z_3$与$z_4$相关，因此有条件分布：

\[p(z_1,z_3,z_5) = p(z_1|z_2)p(z_3|z_4)p(z_5)\]

作者假设$p(z_1|z_2)$,$p(z_3|z_4)$,$p(z_5)$为正态分布，其中$p(z_1|z_2)$的均值和方差通过$z_2$计算(用卷积层回归)，$p(z_3|z_4)$的均值和方差通过$z_4$计算，而$p(z_5)$的均值和方差直接学习得到。

如果仍然构造一个符合标准正态分布的隐变量$\hat{z}=[\hat{z}_1,\hat{z}_3,\hat{z}_5]$，相当于对输出再进行一次变换：

\[\hat{z}_1 = \frac{z_1-\mu(z_2)}{\sigma(z_2)},\hat{z}_3 = \frac{z_3-\mu(z_4)}{\sigma(z_4)},\hat{z}_5 = \frac{z_5-\mu(z_5)}{\sigma(z_5)}\]

⚪ 优化目标

优化目标为最大化对数似然：

\[\log p_X(x) = \log p_Z(\hat{z}) + \log |\det[\frac{\partial f(x)}{\partial x}]|\]

其中Real NVP模型表示为$\hat{z}=f(x)$。隐变量$\hat{z}$的先验分布$p_Z(\hat{z})$预设为各分量独立的标准正态分布：

\[p_Z(\hat{z}) = \frac{1}{(\sqrt{2\pi})^D}e^{-\frac{1}{2}||\hat{z}||^2}\]

则优化目标表示为：

\[\log p_X(x) ~ -\frac{1}{2}||f(x)||^2 + \log |\det[\frac{\partial f(x)}{\partial x}]|\]

在Jacobian行列式$\det[\frac{\partial f(x)}{\partial x}]$中，既包含仿射耦合层贡献的变换$s$输出各元素的乘积，也包含强制隐变量标准化导致的变换行列式$-\sum \log \sigma$。

值得一提的是，Real NVP模型中使用了BatchNorm层，也会带来变换行列式$-\sum \log \tilde{\sigma}$。