Memory Augmented Neural Network.

RNN中的隐状态可以看作一种内部记忆，但这种记忆不能存储太多的信息；可以在神经网络中引入外部记忆(External Memory)单元来提高网络容量。

装备外部记忆的神经网络称为记忆增强神经网络（Memory Augmented Neural Network，MANN），或简称为记忆网络（Memory Network，MN）。

本文目录：

记忆网络的典型结构
端到端记忆网络
神经图灵机

1. 记忆网络的典型结构

记忆网络的模块包括：

主网络$C$，也叫控制器；负责信息处理，以及与外界的交互；
外部记忆单元$M$,用来存储信息；可以用一组向量$M = [m_1,...,m_N]$表示；
读取模块$R$：根据主网络生成的查询向量$q_r$，从外部记忆单元读取信息；
写入模块$W$：根据主网络生成的查询向量$q_w$和要写入的信息$a$，更新外部记忆单元。

读取或写入操作通常使用注意力机制实现，以读取为例：

\[α_n = softmax(s(q_r,m_n))\] \[r = \sum_{n=1}^{N} {α_nm_n}\]

2. 端到端记忆网络

paper：End-To-End Memory Networks

端到端记忆网络（End-To-End Memory Network，MemN2N）是一种可微的网络结构，外部记忆单元是只读的；可以多次从外部记忆中读取信息。

将存储的信息$M = [m_1,...,m_N]$转换成两组记忆片段(Memory Segment)：

$A = [a_1,...,a_N]$用于寻址；
$C = [c_1,...,c_N]$用于输出。

主网络根据输入$x$生成$q$，并使用键值对注意力机制来从外部记忆中读取相关信息$r$:

\[r = \sum_{n=1}^{N} {softmax(s(a_n,q))c_n}\] \[y = f(q+r)\]

为了实现更复杂的计算，可以让主网络和外部记忆进行多轮交互,即多跳（Multi-Hop）操作。

在第$k$轮交互中，主网络根据上次从外部记忆读取的信息$r^{(k-1)}$，产生新的查询向量：

\[q^{(k)} = r^{(k-1)}+q^{(k-1)}\]

第$k$轮交互：

\[r^{(k)} = \sum_{n=1}^{N} {softmax(a_n^{(k)}q^{(k)})c_n^{(k)}}\]

多跳操作的参数是共享的，每轮交互的外部记忆也可以共享使用。

3. 神经图灵机

paper：Neural Turing Machines

Alan Turing在1936年提出了一个最小计算模型：图灵机(Turing Machine)。它由一条无限长的纸带(tape)和一个与纸带相互作用的探针(head)组成。纸带上有无数个单元，每个单元都填充了一个符号：$0$、$1$或空白（“ ”）。探针可以读取符号、编辑符号，并在纸带上向左/向右移动。理论上图灵机可以模拟任何计算机算法。

神经图灵机（Neural Turing Machine，NTM）是一种带有外部记忆单元的神经网络。其中外部记忆是可读写的，用于模拟图灵机的纸带。神经图灵机由控制器(controller)和外部记忆(Memory)单元构成。控制器对记忆单元执行操作，可以通过任意形式的神经网络实现；记忆单元由$N$个维度为$M$的向量组成的矩阵，用于存储处理的信息。

在每一时刻$t$，控制器接收当前时刻的输入$x_t$、上一时刻的输出$h_{t-1}$和上一时刻读取的信息$r_{t-1}$，并产生输出$h_{t}$，同时生成和读写外部记忆相关的三个向量：查询(query)向量$q_{t}$、删除(erase)向量$e_{t}$和增加(add)向量$a_{t}$。

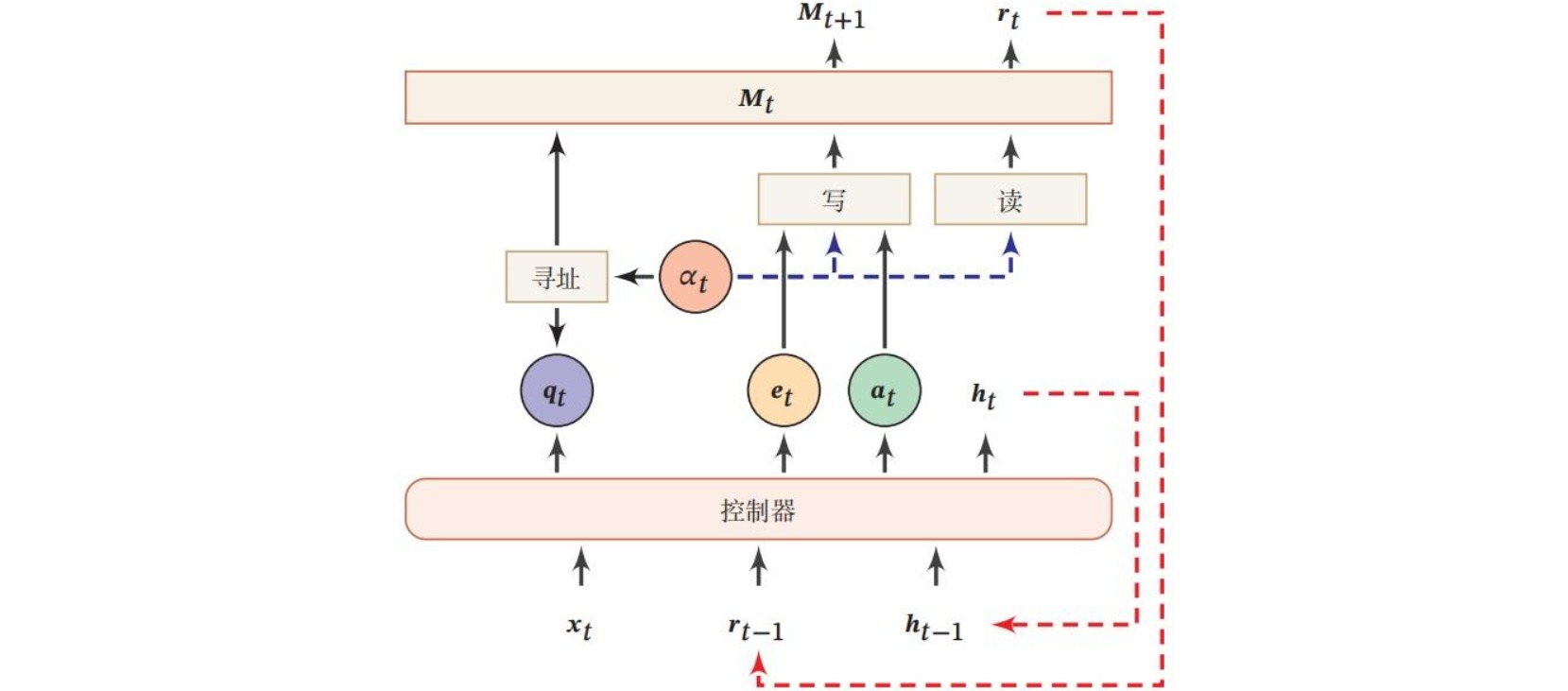
神经图灵机的读操作是通过注意力机制实现的。在每一时刻$t$构造注意力分布$(α_{t,1},…,α_{t,n})$，然后从外部记忆中读取信息$r_{t}$：

\[r_t = \sum_{n=1}^{N} {α_{t,n}m_{t,n}}\]

神经图灵机的写操作参考了LSTM的输入门和遗忘门，包括删除$e_{t}$和增加$a_{t}$：

\[m_{t+1,n} = m_{t,n}(1-α_{t,n}e_t)+α_{t,n}a_t\]

神经图灵机中的注意力机制采用了基于上下文(content-based)和基于位置(location-based)的寻址(addressing)机制。

基于上下文的寻址是指把控制器生成的查询向量$q_{t}$作用于外部记忆单元$M_t=[m_{t,1},...,m_{t,N}]$，通过余弦相似度衡量相似性并通过softmax函数归一化。此外还引入了一个强度权重$\beta_t$以调整注意力的关注程度：

\[w_{t,n} = \text{softmax}(\beta_t\cdot \text{cosine}[q_t,m_{t,n}]) = \frac{\exp(\beta_t \frac{q_t\cdot m_{t,n}}{||q_t|| \cdot ||m_{t,n}||})}{\sum_{i=1}^N \exp(\beta_t \frac{q_t\cdot m_{t,i}}{||q_t|| \cdot ||m_{t,i}||})}\]

然后通过一个插值门控标量$g_t$融合新生成的上下文注意力向量和上一时刻的注意力权重：

\[w_t^g = g_t w_t^c + (1-g_t)w_{t-1}\]

基于位置的寻址是指通过加权分布对注意力向量中不同位置的值进行调整，相当于应用一个一维卷积核$s_t(\cdot)$：

\[\tilde{w}_{t,n} = \sum_{j=1}^N w_{t,j}^gs_{t,n-j}\]

卷积核的形式可以设置为：