广义人体姿态估计中的自校正与自适应推理.
本文为人体姿态估计任务设计了一种可以自修正和自适应的推理方法 (Self-correctable and adaptable inference, SCAI),该方法提出了一种修正网络,能在完全没有标注的测试样本上进行训练,逐步修正预测结果,带来显著的性能提升。
SCAI方法的输入$u$直接是姿态模型预测的Heatmap,SCAI 中一共包含了三个需要训练的网络。

⚪ 预测网络 $\Phi$
预测网络的输入是一组关节点 Heatmap,输出是与之相关联的下一个关节点。更具体地讲,预测的是远端关节点,也就是手腕点、脚踝点这种位于肢体最外侧的节点,这些关节点往往具有最大的自由度,作者在误差分析中也发现大部分的预测误差来自于对这些远端关节点的预测。
为了简化问题,作者手工将人体关节点分成了$6$组,从而使得每一组的关节点都是一条直链。经过分组后,每一组都正好只有 $4$ 个节点,即有一个近端关节点$H_A$、一个远端关节点$H_D$,和两个中间节点$H_B,H_C$。预测网络的工作就是输入 $H_A,H_B,H_C$,来预测远端关节点$\hat{H}_D$。
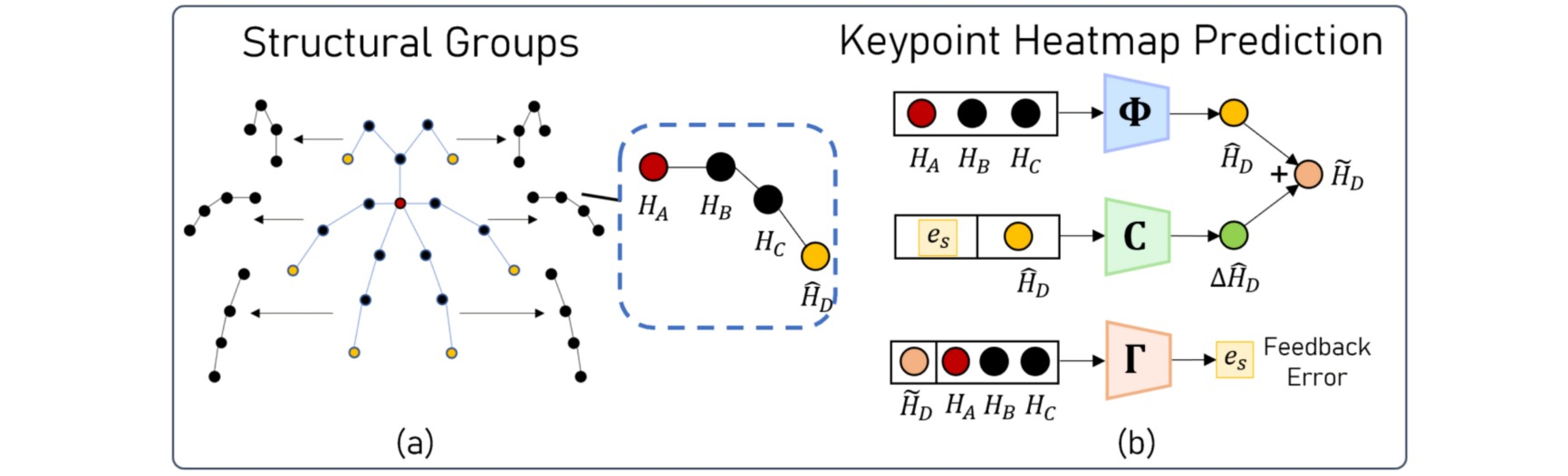
⚪ 修正网络 $C$
修正网络对预测得到的$\hat{H}_D$进行修正,它的输入是$\hat{H}_D$和一个 self-referential feedback error $e_s$,预测一个修正的偏移量$\Delta \hat{H}_D$,这个偏移量可以直接加到原来的$\hat{H}_D$上完成修正,修正后的远端关节点记为$\tilde{H}_D=\hat{H}_D+\Delta \hat{H}_D$。
⚪ 误差反馈网络 $\Gamma$
$e_s$由误差反馈网络提供,衡量了这次预测的误差,为修正网络提供了重要的参考。误差反馈网络的输入是 $H_B,H_C,\tilde{H}_D$,也就是两个中间节点加上修正后的远端节点,来预测近端关节点$H_A$,而$H_A$与$\hat{H}_A$的误差可以反映修正结果。因此$e_s$为$H_A$与$\hat{H}_A$之差的二范数:
\[e_s = ||H_A-\hat{H}_A||_2\]⚪ 训练过程
对于预测网络$\Phi$,训练损失就是预测的$\hat{H}_D$与$H_D$的误差二范数:
\[L_\Phi = ||H_D-\hat{H}_D||_2\]对于误差反馈网络$\Gamma$,损失为$\hat{H}_A$与$H_A$之差的二范数:
\[L_\Gamma = ||H_A-\hat{H}_A||_2\]对于修正网络$C$,损失计算为:
\[\begin{aligned} L_C &= a\cdot L_C^0 + b\cdot L_C^1 + \lambda \cdot (L_C^1-L_C^2) \\ L_C^0 &= ||H_D-\tilde{H}_D||_2 \\ L_C^1 & = ||H_A-\hat{H}_A||_2 \\ L_C^2 & = ||H_A-\Gamma(H_B,H_C,\hat{H}_D)||_2 \\ \end{aligned}\]其中远端修正损失$L_C^0$用于监督预测网络去预测正确的远端关节点位置,近端误差损失$L_C^1$用于监督误差反馈网络去预测正确的近端关节点位置,$L_C^1-L_C^2$用于监督修正网络更好地进行修正。
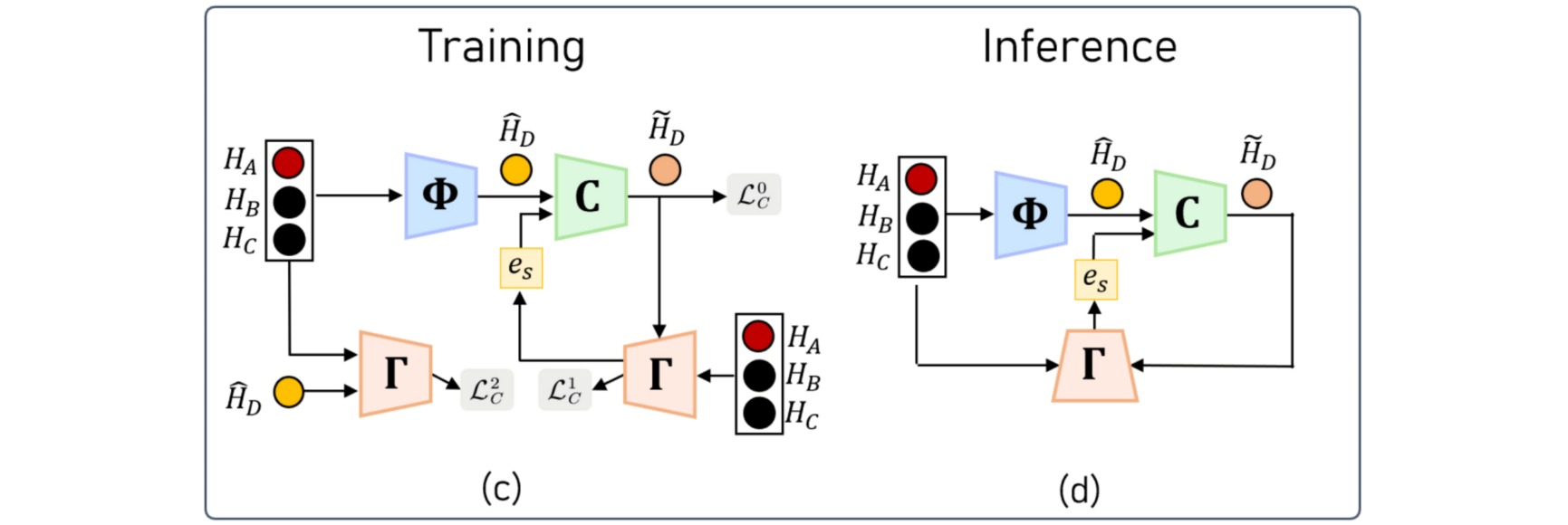
⚪ 推理过程
推理阶段,三个网络共同使用,在测试时提升预测的精度。这个修正网络并不仅仅在有标注的数据上可以训练,还能在无标注的测试数据上继续训练。


