Metric Learning.

度量学习(Metric Learning)是指在特定的任务上通过理解样本之间的相似关系，学习一个合适的距离度量函数。传统的度量学习方法通常使用线性投影将原始数据的特征空间转化为具有距离信息的新的变换空间，然后在变换空间中应用常用的距离度量函数衡量样本之间的相似性。

给定数据集\(\{(x_i,y_i)\}\)，深度度量学习通过共享权重的深度神经网络$f_{\theta}(\cdot)$把原始样本$x$映射到低维特征空间，并设计合理的度量损失使得同类样本在特征空间上的距离比较近，不同类样本之间的距离比较远；从而可以近似实现不同样本的相似度评估，进而应用在人脸识别、行人重识别、图像检索等依赖于样本对匹配的任务中。

本文目录：

  1. 正负样本的采样
  2. 网络结构的设计
  3. 损失函数的设计
  4. 使用PyTorch Metric Learning实现度量学习

1. 正负样本的采样

度量学习的目标在于最小化相似样本之间的距离，最大化不相似样本之间的距离。因此对于输入样本$x$ (称为anchor样本)，需要合理地选择正样本(相似样本)和负样本(不相似样本)。

在深度度量学习中，负样本对的数量(不同标签的样本)通常远大于正样本对(相同标签的样本)的数量。如果采用简单的随机样本采样策略，即随机选择两个不相似的样本分别作为正负样本，则网络的学习过程可能会受到限制。主要原因是存在低质量的负样本对无法为网络带来有用的信息，因此通过负样本挖掘(negtive mining)策略选择负样本。

2. 网络结构的设计

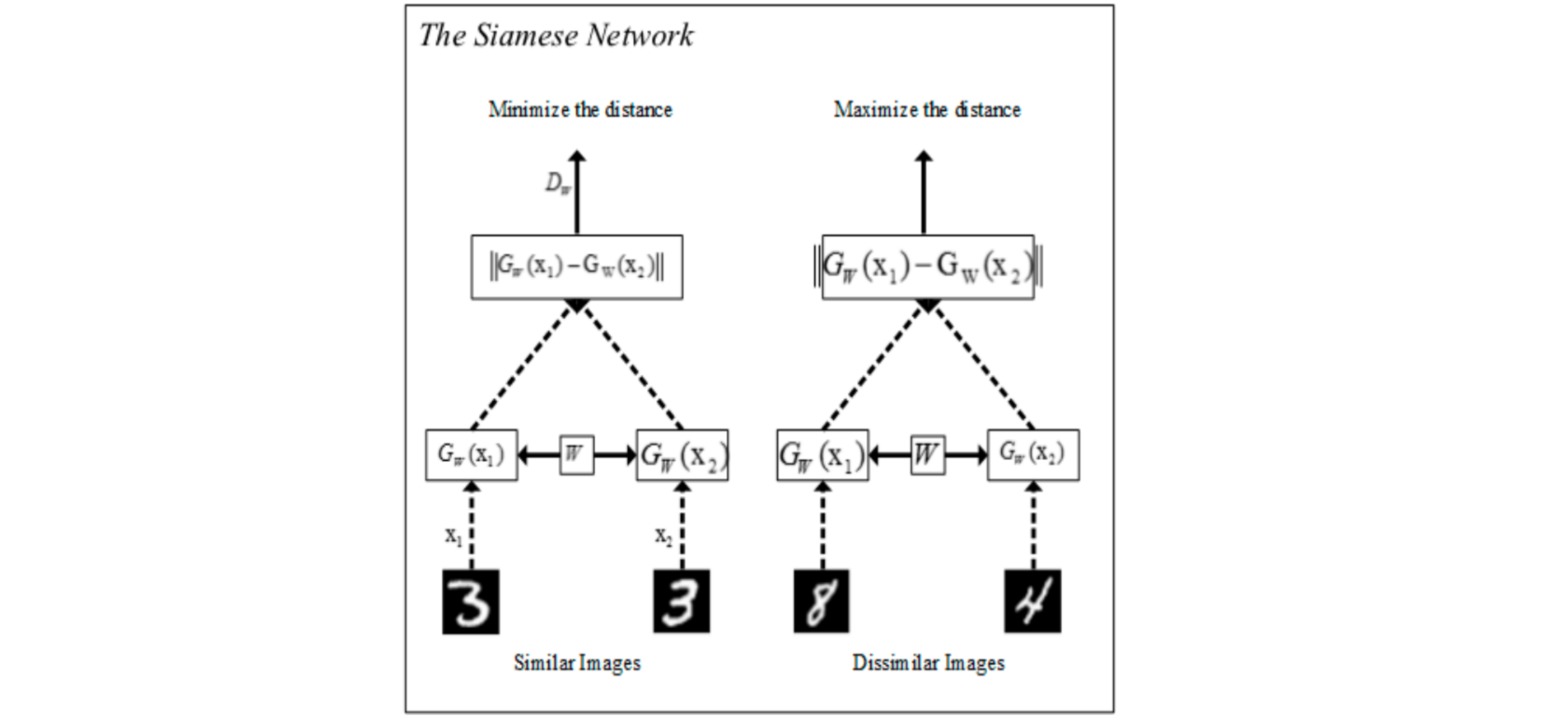
深度度量学习使用深度神经网络衡量样本对的距离。典型结构是Siamese网络，通过共享权重的网络分别接收成对的图像(包括正、负样本)，通过损失函数计算成对图像之间的距离。Siamese网络的本质是对同一个网络执行两次前向传播。

3. 损失函数的设计

(1) 基于对的度量损失 Pair-based Metric Loss

基于对(Pair-based)的度量损失考虑一个批次样本中样本对之间的关系，最小化正样本对之间的距离，最大化负样本对之间的距离。样本对之间的关系既可以是局部的(考虑少数几个样本)，也可以是非局部的(考虑一个批次的所有样本)。

⚪ Contrastive Loss

对比损失(Contrastive Loss)判断给定的样本对$(x_i,x_j)$之间的正负关系，若为正样本对则使其特征距离接近$0$，若为负样本对则使其特征距离不小于$\epsilon$。

\[\Bbb{I}(y_i=y_j) D[f_{\theta}(x_i),f_{\theta}(x_j)] + \Bbb{I}(y_i\neq y_j) \max(0,\epsilon- D[f_{\theta}(x_i),f_{\theta}(x_j)])\]

⚪ Binomial Deviance Loss

二项式偏差损失(Binomial Deviance Loss)是对比损失的软化版本，使用softplus函数代替Hinge loss：

\[\Bbb{I}(y_i=y_j) \log(1+\exp(\alpha(D[f_{\theta}(x_i),f_{\theta}(x_j)]-\lambda))) \\ + \Bbb{I}(y_i\neq y_j) \log(1+\exp(\beta(\lambda- D[f_{\theta}(x_i),f_{\theta}(x_j)])))\]

⚪ Triplet Loss

三元组损失(triplet loss)为每一个样本$x$选择一个正样本$x^+$和一个负样本$x^-$，使得正样本对之间的距离比负样本对之间的距离小于margin值$\epsilon$。

\[\max(0, D[f_{\theta}(x),f_{\theta}(x^+)] -D[f_{\theta}(x),f_{\theta}(x^-)] + \epsilon)\]

⚪ Improved Triplet Loss

Improved Triplet Loss在Triplet Loss的基础上约束正样本对的距离不超过$\beta < \alpha$：

\[\max(0, D[f_{\theta}(x),f_{\theta}(x^+)] -D[f_{\theta}(x),f_{\theta}(x^-)] + \alpha) \\ + \max(0, D[f_{\theta}(x),f_{\theta}(x^+)] - \beta)\]

⚪ Batch Hard Triplet Loss

Batch Hard Triplet Loss对每一个样本$x$选择$K$个正样本$x^+_k$和$K$个负样本$x^-_k$，并选用最难的正样本对和负样本对构造损失：

\[\max(0, \mathop{\max}_k D[f_{\theta}(x),f_{\theta}(x^+_k)] - \mathop{\min}_k D[f_{\theta}(x),f_{\theta}(x^-_k)] + \epsilon)\]

⚪ Hierarchical Triplet Loss

分层三元组损失(Hierarchical Triplet Loss)根据数据集构造分层树，对其进行Anchor neighbor采样生成三元组，并根据构造的分层树的类间关系设置violate margin:

\[\alpha_z = \beta + d_{H(y_a,y_n)} - S_{y_a}\]

⚪ Angular Loss

角度损失(angular loss)引入了三元组$(x_a,x_p,x_n)$的三阶几何限制，具有尺度不变性和旋转不变性。构造anchor样本$x_a$和正样本$x_p$的中心点$x_c=(x_a+x_p)/2$，并以其为圆心作圆；连接$x_n$与$x_c$后作垂线与圆相交于点$x_m$。若角度$n’$减小，则负样本$x_n$沿着$x_cx_n$方向远离样本$x_a$和正样本$x_p$，而样本$x_a$和正样本$x_p$彼此接近。

\[\max(0, D[f_{\theta}(x_a),f_{\theta}(x_p)] -4 \tan^2 \alpha D[f_{\theta}(x_n),f_{\theta}(x_c)||^2])\]

⚪ Quadruplet Loss

四元组损失(Quadruplet Loss)为每一个样本$x$选择一个正样本$x^+$和两个负样本$x^-_1,x^-_2$，使得正样本对之间的距离同时小于负样本对之间的距离和两个负样本之间的距离：

\[\max(0, D[f_{\theta}(x),f_{\theta}(x^+)] -D[f_{\theta}(x),f_{\theta}(x^-_1)] + \alpha) \\ + \max(0, D[f_{\theta}(x),f_{\theta}(x^+)] -D[f_{\theta}(x^-_2),f_{\theta}(x^-_1)] + \beta)\]

⚪ N-pair Loss

N-pair Loss把Triplet损失扩展到同时比较所有负类样本的距离。对于每一个样本$x$，选择一个正样本$x^+$和所有其他类别的负样本$x_1^-,…,x_{N-1}^-$构造$(N+1)$元组，则N-pair损失定义为：

\[- \log\frac{\exp(f_{\theta}(x)^Tf_{\theta}(x^+))}{\exp(f_{\theta}(x)^Tf_{\theta}(x^+))+ \sum_{i=1}^{N-1} \exp(f_{\theta}(x)^Tf_{\theta}(x_i^-))}\]

⚪ Lifted Structured Loss

Lifted Structured Loss根据一批样本内的所有样本对之间的关系动态地构建最困难的三元组。对于每一个正样本对$(i,j)$，分别找到距离$i$最近的负样本$k$和距离$j$最近的负样本$l$，选择其中距离较小的负样本$n \in (k,l)$构建三元组$(i,j,n)$。

\[\frac{1}{2| \mathcal{P}|} \sum_{(i,j) \in \mathcal{P}} \max(0,D_{ij} + \max(\mathop{\max}_{(i,k) \in \mathcal{N}} \epsilon-D_{ik},\mathop{\max}_{(j,l) \in \mathcal{N}} \epsilon-D_{jl}))^2\]

⚪ Histogram Loss

直方图损失(Histogram Loss)首先估计正样本对和负样本对所对应的两个特征距离分布$p^+(x),p^-(x)$（通过直方图$H^+$和$H^-$近似），然后计算正样本对之间的相似度比负样本对之间的相似度还要小的概率：

\[\int_{-1}^{1}p^-(x) [\int_{-1}^{x}p^+(y)dy] dx ≈ \sum_{r=1}^R (h^-_r \sum_{q=1}^rh_q^+)\]

⚪ Ranked List Loss

给定anchor样本$x_i^c$后Ranked List Loss基于相似度对其他样本进行排序，然后选择$N_c-1$个距离大于$\alpha-m$的正样本和$N_k$个距离小于$\alpha$的负样本，希望负样本对的距离大于某个阈值$\alpha$，并且正样本对的距离小于$\alpha-m$：

\[\frac{1}{N_c-1} \sum_{j=1}^{N_c-1} \max(0,D[f_{\theta}(x_i),f_{\theta}(x_j)] - (\alpha-m)) \\ + \sum_{j=1}^{N_k} \frac{w_{ij}}{\sum_{j=1}^{N_k}w_{ij}} \max(0,\alpha- D[f_{\theta}(x_i),f_{\theta}(x_j)])\]

⚪ Soft Nearest Neighbor Loss

Soft Nearest Neighbor Loss用于在表征空间中度量不同类别数据的纠缠度。给定数据集\(\{x_i,y_i\}_{i=1}^N\)，该损失定义为：

\[-\frac{1}{N} \sum_{i=1}^N \log \frac{\sum_{i\neq j,y_i=y_j,j=1,...,N} \exp(-f(x_i,x_j)/ \tau)}{\sum_{i\neq k,k=1,...,N} \exp(-f(x_i,x_k)/ \tau)}\]

⚪ Multi-Similarity Loss

Multi-Similarity Loss把基于对的深度度量损失公式化为一种对样本对距离进行加权的通用对加权形式，然后通过自相似性和相对相似性分别为正负样本对赋权。

\[\frac{1}{\alpha} \log(1+\sum_{k \in \mathcal{P}_i} e^{\alpha(D_{ik}+\lambda)}) + \frac{1}{\beta} \log(1+\sum_{k \in \mathcal{N}_i} e^{-\beta(D_{ik}+\lambda)})\]

⚪ Circle Loss

Circle Loss对欠优化的样本对距离进行重新加权，使得样本对距离远离最优中心的样本对被更多的关注和惩罚。

\[\log(1+ \sum_{j \in \mathcal{N}_i} \exp(-\gamma\alpha_n^j(D_{ij}+\Delta_n))\sum_{k \in \mathcal{P}_i} \exp(\gamma\alpha_p^k(D_{ik}+\Delta_p)))\]

(2) 基于代理的度量损失 Proxy-based Metric Loss

基于代理(Proxy-based)的度量损失为每个类别赋予一个代理样本，拉近每个类别的样本和该类别的代理样本之间的距离，拉远与其他类别的代理样本之间的距离。代理样本既可以通过给定数据集生成，也可以设置为可学习向量。

⚪ Magnet Loss

Magnet Loss检索聚类簇的所有邻域聚类簇，最小化每个聚类簇中的样本与对应样本均值的距离，并最大化与其他簇的样本均值的距离：

\[-\log \frac{e^{-\frac{1}{2\sigma^2}||f_{\theta}(x^c)-\mu_c||_2^2-\alpha}}{\sum_{\mu: c(\mu) \neq c}e^{-\frac{1}{2\sigma^2}||f_{\theta}(x^c)-\mu||_2^2}}\]

⚪ Clustering Loss

Clustering Loss预先为每个类别的样本指定一个聚类中心，要求最佳聚类得分\(\tilde{F}\)比任意其他聚类划分$g(S)$的聚类得分不低于结构化边界$\Delta$：

\[\max(0, \mathop{\max}_{S \subset V,|S| = |Y|} \{ F(X,S;\theta)+\gamma \Delta(g(S),Y) \} - \tilde{F}(X,Y;\theta) )\]

⚪ Proxy-NCA

Proxy-NCA为每个类别随机初始化一个代理向量$p$，遍历样本时以邻域成分分析(NCA)的形式拉近每个样本$x$和该样本类别$y$对应的代理向量$p_y$之间的距离，增大和其他类别的代理向量$p_z$之间的距离。

\[-\log (\frac{\exp(-D[f_{\theta}(x),p_y])}{\sum_{z \neq y} \exp(-D[f_{\theta}(x),p_z])})\]

⚪ ProxyNCA++

ProxyNCA++在Proxy-NCA的基础上引入了一些改进，其中对损失函数的改进包括优化代理分配概率和低温缩放。

\[-\log (\frac{\exp(-D[f_{\theta}(x),p_y]/T)}{\sum_{z} \exp(-D[f_{\theta}(x),p_z]/T)})\]

⚪ Proxy-Anchor

Proxy-Anchor为每个类别随机初始化一个代理向量$p$，遍历每一个代理向量，减少该类别的所有样本与该代理向量的距离，增大其他类别的样本与该代理向量的距离。

\[\frac{1}{|P^+|} \sum_{p \in P^+} \log (1+\sum_{x \in X_p^+}e^{\alpha(D[f_{\theta}(x),p]+\delta)}) \\+ \frac{1}{|P|} \sum_{p \in P} \log (1+\sum_{x \in X_p^-}e^{-\alpha(D[f_{\theta}(x),p]-\delta)})\]

⭐ 参考文献

4. 使用PyTorch Metric Learning实现度量学习

PyTorch Metric Learning库是一个为深度度量学习设计的第三方库，安装方式如下：

pip install pytorch-metric-learning

首先初始化一个度量损失函数，以计算训练集中样本对的度量损失：

from pytorch_metric_learning import losses
loss_func = losses.TripletMarginLoss()

通常正样本对由共享相同标签的特征嵌入构成，负样本对由具有不同标签的特征嵌入构成；可以通过设置采样策略构造样本对的难例挖掘：

from pytorch_metric_learning import miners
miner = miners.MultiSimilarityMiner()

在训练过程中传入模型构造的特征嵌入（尺寸为(batch_size, embedding_size)）以及相应的标签（尺寸为(batch_size)）：

# your training loop
for i, (data, labels) in enumerate(dataloader):
    optimizer.zero_grad()
    embeddings = model(data)
    hard_pairs = miner(embeddings, labels)
    loss = loss_func(embeddings, labels, hard_pairs)
    loss.backward()
    optimizer.step()

损失函数可通过distances, reducers, regularizers定义。通过难例挖掘可以找到不同的样本对索引，然后通过定义的距离函数计算样本对之间的距离，并进一步计算损失函数；正则化器则为每个样本计算正则化损失；然后通过衰减器仅保留数值较高的损失项。

from pytorch_metric_learning.distances import CosineSimilarity
from pytorch_metric_learning.reducers import ThresholdReducer
from pytorch_metric_learning.regularizers import LpRegularizer
from pytorch_metric_learning import losses
loss_func = losses.TripletMarginLoss(distance = CosineSimilarity(), 
                                    reducer = ThresholdReducer(high=0.3), 
                                    embedding_regularizer = LpRegularizer())