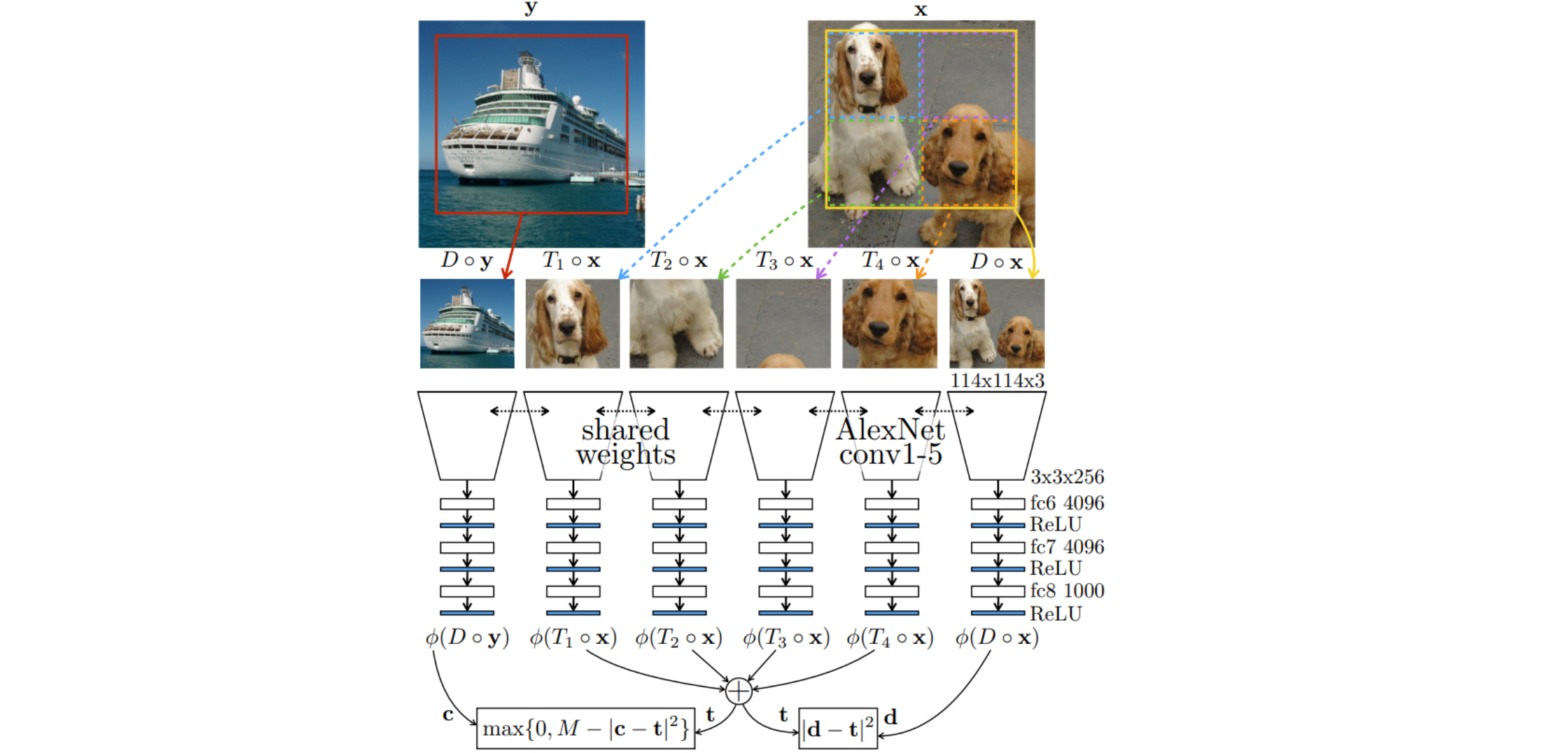
通过学习计数实现无监督表示学习.
本文提出把图像的特征或者视觉基元(visual primitive)看作一种标量属性,可以通过不同图像块求和或在图像块之间进行比较,因此图像块之间的关系可以通过特征计数定义。
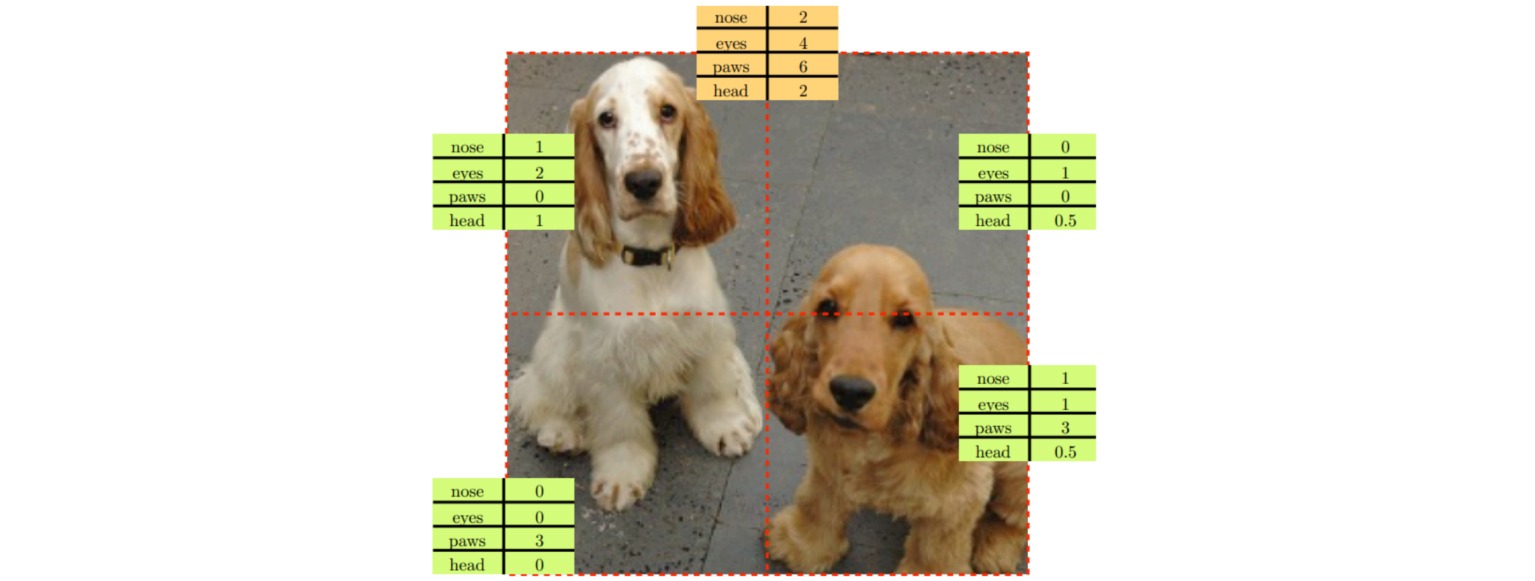
定义图像的两种变换:
- 缩放(scaling):如果一幅图像尺寸缩小或放大两倍,其中的视觉基元数量不改变;
- 平铺(tiling):如果把一幅图像划分成$2\times 2$的图像块,则四个图像块中视觉基元的数量之和应该与原始图像的特征数量相同。
此时把模型看作特征计数器$\phi(\cdot)$,用于评估输入图像中视觉基元的数量。对于输入图像$x$,定义$2\times$下采样操作$D(\cdot)$和$2\times 2$图像块划分操作$T_i(\cdot),i=1,2,3,4$,则特征计数存在如下关系:
\[\phi(x) = \phi(D \circ x) = \sum_{i=1}^4 \phi(T_i \circ x)\]因此构造两者的均方误差损失:
\[\mathcal{L}_{\text{feat}} = ||\phi(D \circ x) - \sum_{i=1}^4 \phi(T_i \circ x)||_2^2\]为了避免平凡解$\phi(x)=0$,额外引入损失使得不同图像$x,y$的特征计数尽可能不同:
\[\mathcal{L}_{\text{diff}} = \max(0,c-||\phi(D \circ y) - \sum_{i=1}^4 \phi(T_i \circ x)||_2^2)\]