深度半监督学习的随机变换和扰动正则化.
- paper:Regularization With Stochastic Transformations and Perturbations for Deep Semi-Supervised Learning
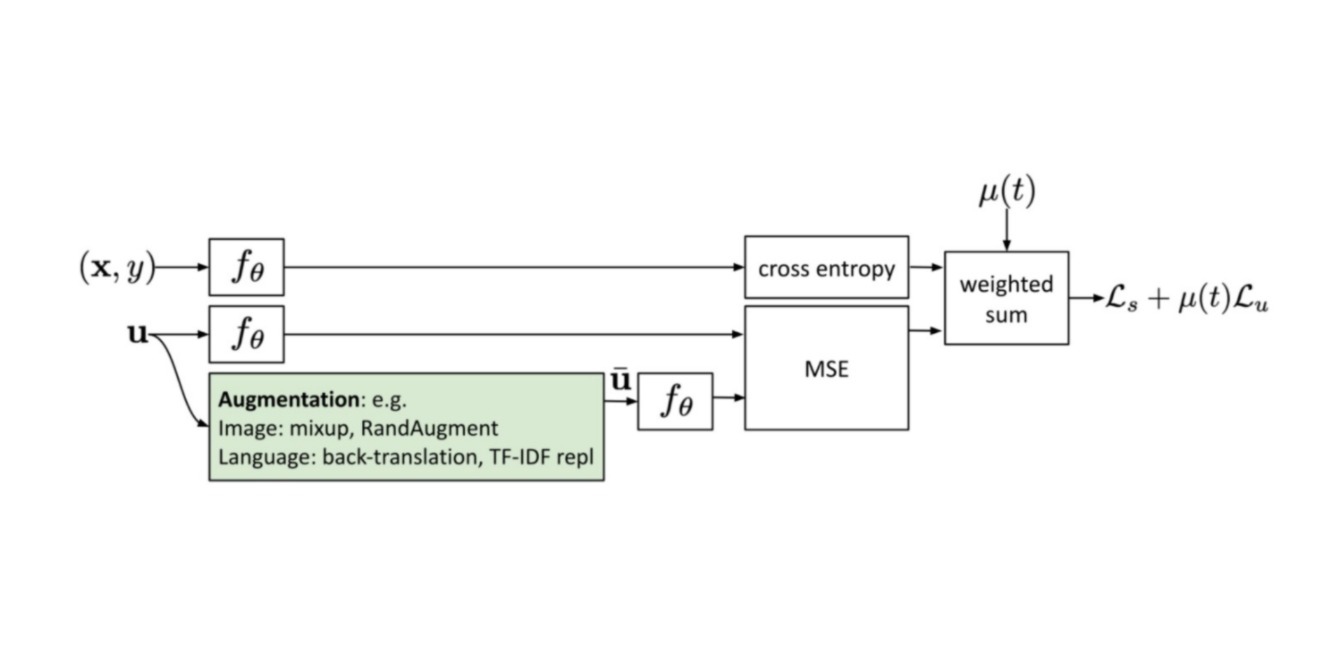
在深度神经网络的训练过程中,通常会对输入样本进行随机转换的数据增强,从而增加模型的随机性,这样可以提高模型的学习能力,降低过拟合的风险。但是随机性的加入也会导致模型预测结果的不稳定,增加模型预测结果的方差。本文提出了一种无监督损失函数,用于保证在利用随机性提高模型性能的同时,降低随机性带来的波动。
该无监督损失旨在最小化一个数据样本两次经过同一个带随机变换(如随即增强或dropout)的网络后预测结果的差异:
\[\mathcal{L}_u^{\Pi} = \sum_{x \in \mathcal{D}} \text{MSE}(f_{\theta}(x),f_{\theta}'(x))\]
由于上述损失函数的定义并没有利用样本的标签信息,仅仅使用上述损失函数训练模型是不够的。对于一个监督学习的分类任务而言,由于样本的标签是一个由0/1编码的向量,所以希望模型$f$对样本的预测向量也尽可能只有一个非0元素,通过互斥损失函数(mutual-exclusivity loss)进行约束。互斥损失函数可以迫使模型预测向量只含有一个非0元素:
\[\mathcal{L}_u^{ME} = \sum_{x \in \mathcal{D}}(-\sum_{c=1}^C f_{\theta}(x)_c \cdot \prod_{k \neq c}^C (1-f_{\theta}(x)_k))\]若样本标签能够获取,则也可以直接构造监督损失:
\[\mathcal{L}_s^{CE} = \sum_{(x,c) \in \mathcal{D}} -\log f_{\theta}(x)_c\]