Position Encoding in Transformer.

Transformer中的自注意力机制无法捕捉位置信息，这是因为其计算过程具有置换不变性(permutation invariant)，导致打乱输入序列的顺序对输出结果不会产生任何影响。

对于Transformer模型$f(\cdot)$，标记输入序列的两个向量$x_m,x_n$，则Transformer具有全对称性：

\[f(\cdots, x_m, \cdots, x_n, \cdots) = f(\cdots, x_n, \cdots, x_m, \cdots)\]

位置编码(Position Encoding)通过把位置信息引入输入序列中，以打破模型的全对称性。为简化问题，考虑在$m,n$位置处加上不同位置编码$p_m,p_n$：

\[\tilde{f}(\cdots, x_m, \cdots, x_n, \cdots) = f(\cdots, x_m+p_m, \cdots, x_n+p_n, \cdots)\]

对上式进行二阶Taylor展开：

\[\tilde{f} ≈ f + \underbrace{p_m^T \frac{\partial f}{\partial x_m} + p_n^T \frac{\partial f}{\partial x_n} + p_m^T \frac{\partial^2 f}{\partial x_m^2}p_m + p_n^T \frac{\partial^2 f}{\partial x_n}p_n}_{\text{绝对位置信息}} +\underbrace{p_m^T \frac{\partial^2 f}{\partial x_m\partial x_n}p_n}_{\text{相对位置信息}}\]

在上式中，第2至5项只依赖于单一位置，表示绝对位置信息。第6项包含$m,n$位置的交互项，表示相对位置信息。因此位置编码主要有两种实现形式：

1. 绝对位置编码 Absolute Position Encoding

绝对位置编码是指在输入序列经过词嵌入后的第$k$个token向量\(x_k \in \Bbb{R}^{d}\)中加入(add)位置向量\(p_k \in \Bbb{R}^{d}\)；其过程等价于首先向输入引入(concatenate)位置索引$k$的one hot向量$p_k: x_k+p_k$，再进行词嵌入；因此绝对位置编码也被称为位置嵌入(position embedding)。

(1) 三角函数式(Sinusoidal)位置编码

三角函数式(Sinusoidal)位置编码是在原Transformer模型中使用的一种显式编码。以一维三角函数编码为例：

\[\begin{aligned} p_{k,2i} &= \sin(\frac{k}{10000^{2i/d}}) \\ p_{k,2i+1} &= \cos(\frac{k}{10000^{2i/d}}) \end{aligned}\]

其中$p_{k,2i},p_{k,2i+1}$分别是位置索引$k$处的编码向量的第$2i,2i+1$个分量。一个长度为$32$的输入序列（每个输入向量的特征维度是$128$）的Sinusoidal编码的可视化如下：

def SinusoidalEncoding1d(seq_len, d_model):
    pos_table = np.array([
        [pos / np.power(10000, 2 * i / d_model) for i in range(d_model)] 
        for pos in range(seq_len)])
    pos_table[1:, 0::2] = np.sin(pos_table[1:, 0::2])  # pos_table[0]作用于[CLS]，不需要位置编码
    pos_table[1:, 1::2] = np.cos(pos_table[1:, 1::2])                
    return torch.FloatTensor(pos_table)

根据三角函数的性质，位置$\alpha+\beta$处的编码向量可以表示成位置$\alpha$和位置$\beta$的向量的组合，因此可以外推到任意位置：

\[\begin{aligned} \sin(\alpha+\beta) &= \sin \alpha \cos \beta + \cos \alpha \sin \beta \\ \cos(\alpha+\beta) &= \cos \alpha \cos \beta - \sin \alpha \sin \beta \end{aligned}\]

在图像领域，常用到二维形式的位置编码。以二维三角函数编码为例，需要分别对高度方向和宽度方向进行编码$p=[p_h,p_w]$：

\[\begin{aligned} p_{h,2i} &= \sin(\frac{h}{10000^{2i/d}}), \quad p_{h,2i+1} = \cos(\frac{h}{10000^{2i/d}}) \\ p_{w,2i} &= \sin(\frac{w}{10000^{2i/d}}), \quad p_{w,2i+1} = \cos(\frac{w}{10000^{2i/d}}) \end{aligned}\] 
def positionalencoding2d(d_model, height, width):
    """
    :param d_model: dimension of the model
    :param height: height of the positions
    :param width: width of the positions
    :return: d_model*height*width position matrix
    """
    if d_model % 4 != 0:
        raise ValueError("Cannot use sin/cos positional encoding with "
                         "odd dimension (got dim={:d})".format(d_model))
    pe = torch.zeros(d_model, height, width)
    # Each dimension use half of d_model
    d_model = int(d_model / 2)
    div_term = torch.exp(torch.arange(0., d_model, 2) *
                         -(math.log(10000.0) / d_model))
    pos_w = torch.arange(0., width).unsqueeze(1)
    pos_h = torch.arange(0., height).unsqueeze(1)
    pe[0:d_model:2, :, :] = torch.sin(pos_w * div_term).transpose(0, 1).unsqueeze(1).repeat(1, height, 1)
    pe[1:d_model:2, :, :] = torch.cos(pos_w * div_term).transpose(0, 1).unsqueeze(1).repeat(1, height, 1)
    pe[d_model::2, :, :] = torch.sin(pos_h * div_term).transpose(0, 1).unsqueeze(2).repeat(1, 1, width)
    pe[d_model+1::2, :, :] = torch.cos(pos_h * div_term).transpose(0, 1).unsqueeze(2).repeat(1, 1, width)
    return pe

(2) 可学习(Learnable)位置编码

可学习(Learnable)位置编码是指将位置编码当作可训练参数，比如输入序列(经过嵌入层后)的大小为$n \times d$，则随机初始化一个\(p \in \Bbb{R}^{n \times d}\)的矩阵作为位置编码，随训练过程更新。

可学习位置编码的缺点是没有外推性，即如果预训练序列的最大长度为$n$，则无法处理长度超过$n$的序列。此时可以将超过$n$部分的位置编码随机初始化并微调。

(3) FLOATER：递归式位置编码

如果位置编码能够递归地生成$p_{k+1}=f(p_k)$，则其生成结构自带学习到位置信息的可能性。

FLOATER使用神经常微分方程(Neural ODE)构建的连续动力系统对位置编码进行递归建模：

\[p(t) = p(s) + \int_{s}^{t} h(\tau,p(\tau);\theta_h) d\tau\]

递归式的FLOATER编码具有更好的灵活性和外推性。但是递归形式的位置编码牺牲了并行性，带来速度瓶颈。

(4) Complex-order：复数式位置编码

绝对位置编码等价于词表索引$j$的词嵌入$x^{(j)}$与位置索引$k$的嵌入$p_k$的求和函数$f(j,k)=x^{(j)}_k+p_k$。Complex-order方法则直接把该函数建模为一个复值函数：

\[f(j, k) = r_je^{i(\theta_j+\omega_j k)}\]

其中振幅$r_j$、角频率$\omega_j$和初相位$\theta_j$是要学习的参数（为同一个词设置三组词嵌入）。振幅$r_j$只和词表索引$j$有关，相当于该词的词嵌入；角频率$\omega_j$表示该词对位置的敏感程度；相位$\theta_j+\omega_j pos$引入该词在文本中的位置信息。

(5) RoPE：旋转式位置编码

旋转式位置编码是指在构造查询矩阵$q$和键矩阵$k$时，根据其绝对位置引入旋转矩阵$\mathcal{R}$：

\[q_i = \mathcal{R}_ix_i W^Q , k_j = \mathcal{R}_jx_j W^K\]

旋转矩阵$\mathcal{R}$设计为正交矩阵，且应满足\(\mathcal{R}_i^T\mathcal{R}_j=\mathcal{R}_{j-i}\)，使得后续注意力矩阵的计算中隐式地包含相对位置信息：

\[(\mathcal{R}_ix_i W^Q)^T(\mathcal{R}_jx_j W^K) = (x_i W^Q)^T\mathcal{R}_i^T\mathcal{R}_jx_j W^K = (x_i W^Q)^T\mathcal{R}_{j-i}x_j W^K\]

(6) 层次化位置编码

在可学习的位置编码中，假设学习到序列长度为$n$的编码，则很难外推到序列长度$>n$的场合。层次化位置编码通过对现有编码进行层次分解，从而利用$n$个编码构造长度为$n^2$的一系列编码。

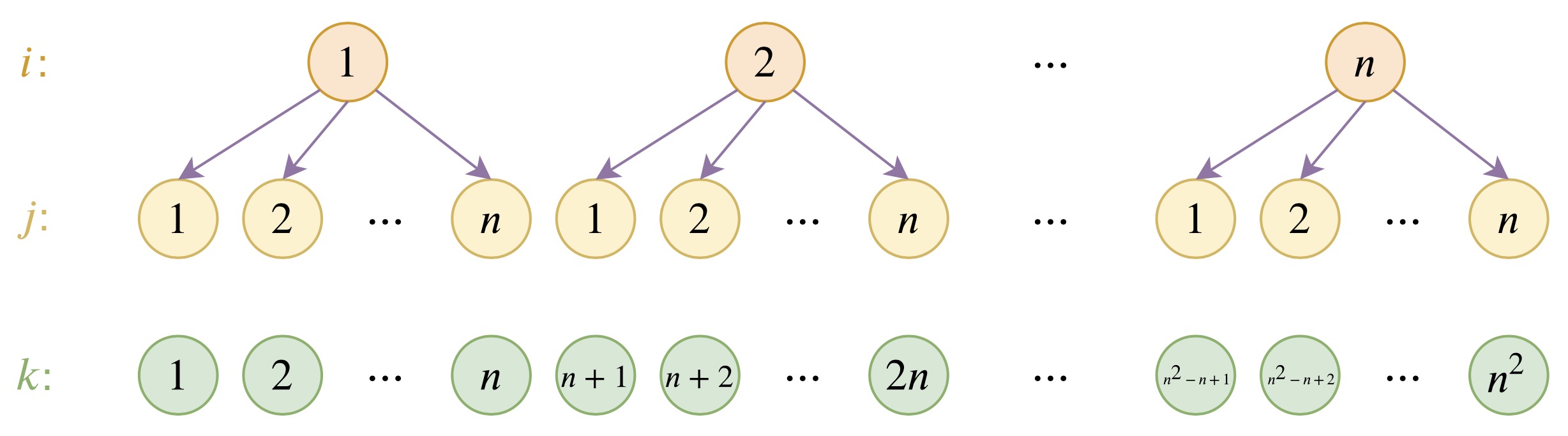
假设学习到位置编码$p_1,p_2,\cdots,p_n$；现构造位置编码$q_1,q_2,\cdots,q_{n^2}$，其是由基编码$u_1,u_2,\cdots,u_n$分层构造的：

\[q_{(i-1)\times n + j} = \alpha u_i + (1-\alpha) u_j\]

其中$\alpha \ne 0.5$是为了区分$(i,j)$和$(j,i)$两种不同的情况。假设前$n$个构造的编码与学习到的编码一致：

\[q_i=p_i, \quad i=1,2,\cdots,n\]

则可以解出基编码：

\[u_i = \frac{p_i-\alpha p_1}{1-\alpha} , \quad i=1,2,\cdots,n\]

2. 相对位置编码 Relative Position Encoding

相对位置编码并不是直接建模每个输入token的位置信息，而是在计算注意力矩阵时考虑当前向量与待交互向量的位置的相对距离。

从绝对位置编码出发，其形式相当于在输入中添加入绝对位置的表示。对应的完整自注意力机制运算如下

\[\begin{aligned} q_i &= (x_i+p_i) W^Q , k_j = (x_j+p_j) W^K ,v_j = (x_j+p_j) W^V \\ \alpha_{ij} &= \text{softmax}\{(x_i+p_i)W^Q ( (x_j+p_j)W^K)^T \} \\ &= \text{softmax}\{ x_iW^Q (W^K)^T x_j^T+x_iW^Q (W^K)^T p_j^T+p_iW^Q (W^K)^T x_j^T+p_iW^Q (W^K)^T p_j^T \} \\ z_i &= \sum_{j=1}^{n} \alpha_{ij}(x_jW^V+p_jW^V) \end{aligned}\]

注意到绝对位置编码相当于在自注意力运算中引入了一系列$p_iW^Q,(p_jW^K)^T,p_jW^V$项。而相对位置编码的出发点便是将这些项调整为与相对位置$(i,j)$有关的向量$R_{i,j}$。

(1) 经典相对位置编码

在经典的相对位置编码设置中，移除了与$x_i$的位置编码项$p_iW^Q$相关的项，并将$x_j$的位置编码项$p_jW^V,p_jW^K$替换为相对位置向量$R_{i,j}^V,R_{i,j}^K$：

\[\begin{aligned} \alpha_{ij} &= \text{softmax}\{x_iW^Q (W^K)^T x_j^T+x_iW^Q (R_{i,j}^K)^T \} \\ z_i &= \sum_{j=1}^{n} \alpha_{ij}(x_jW^V+R_{i,j}^V) \end{aligned}\]

相对位置向量$R_{i,j}^V,R_{i,j}^K$可以设置为三角函数式或可学习参数，并且通常只考虑相对位置$p_{\min} \leq i-j \leq p_{\max}$的情况：

\[\begin{aligned} R_{i,j}^K &= w^K_{\text{clip}(j-i,p_{\min},p_{\max})} \in (w_{p_{\min}}^K,\cdots w_{p_{\max}}^K) \\ R_{i,j}^V &= w^V_{\text{clip}(j-i,p_{\min},p_{\max})} \in (w_{p_{\min}}^V,\cdots w_{p_{\max}}^V) \end{aligned}\]

(2) XLNet式

在XLNet模型中，移除了值向量的位置编码$p_j$，并将注意力计算中$x_j$的位置编码$p_j$替换为相对位置向量$R_{i-j}$(设置为三角函数式编码)，$x_i$的位置编码$p_i$设置为可学习向量$u,v$：

\[\begin{aligned} \alpha_{ij} &= \text{softmax}\{ x_iW^Q (W^K)^T x_j^T+x_iW^Q (W^K)^T R_{i-j}^T+uW^Q (W^K)^T x_j^T+vW^Q (W^K)^T R_{i-j}^T \} \\ z_i &= \sum_{j=1}^{n} \alpha_{ij}x_jW^V \end{aligned}\]

(3) T5式

在T5模型中，移除了值向量的位置编码$p_j$以及注意力计算中的输入-位置注意力项($x_i,p_j$和$p_i,x_j$)，并将位置-位置注意力项($p_i,p_j$)设置为可学习标量$r_{i,j}$：

\[\begin{aligned} \alpha_{ij} &= \text{softmax}\{ x_iW^Q (W^K)^T x_j^T+r_{i,j} \} \\ z_i &= \sum_{j=1}^{n} \alpha_{ij}x_jW^V \end{aligned}\]

一维形式的T5式相对位置编码的实现过程如下：

class Attention(nn.Module):
    def __init__(self, dim, seq_len, heads = 8, dim_head = 64, dropout = 0.):
        super().__init__()
        inner_dim = dim_head *  heads
        project_out = not (heads == 1 and dim_head == dim)

        self.heads = heads
        self.scale = dim_head ** -0.5

        self.attend = nn.Softmax(dim = -1)
        self.dropout = nn.Dropout(dropout)

        self.to_qkv = nn.Linear(dim, inner_dim * 3, bias = False)

        self.to_out = nn.Sequential(
            nn.Linear(inner_dim, dim),
            nn.Dropout(dropout)
        ) if project_out else nn.Identity()

        # positional bias

        self.pos_bias = nn.Embedding(seq_len, heads)

        q_pos = torch.arange(seq_len)
        k_pos = torch.arange(seq_len)

        pos_indices = (q_pos[:, None] - k_pos[None, :]).abs()

        self.register_buffer('pos_indices', pos_indices)

    def apply_pos_bias(self, fmap):
        bias = self.pos_bias(self.pos_indices)
        bias = rearrange(bias, 'i j h -> () h i j')
        return fmap + (bias / self.scale)

    def forward(self, x):
        qkv = self.to_qkv(x).chunk(3, dim = -1)
        q, k, v = map(lambda t: rearrange(t, 'b n (h d) -> b h n d', h = self.heads), qkv)

        dots = torch.matmul(q, k.transpose(-1, -2)) * self.scale

        # 引入相对位置编码
        dots = self.apply_pos_bias(dots)

        attn = self.attend(dots)
        attn = self.dropout(attn)

        out = torch.matmul(attn, v)
        out = rearrange(out, 'b h n d -> b n (h d)')
        return self.to_out(out)

二维形式的T5式相对位置编码的实现过程如下：

class Attention(nn.Module):
    def __init__(self, dim, fmap_size, heads = 8, dim_head = 64, dropout = 0.):
        super().__init__()
        inner_dim = dim_head *  heads
        project_out = not (heads == 1 and dim_head == dim)

        self.heads = heads
        self.scale = dim_head ** -0.5

        self.attend = nn.Softmax(dim = -1)
        self.dropout = nn.Dropout(dropout)

        self.to_qkv = nn.Linear(dim, inner_dim * 3, bias = False)

        self.to_out = nn.Sequential(
            nn.Linear(inner_dim, dim),
            nn.Dropout(dropout)
        ) if project_out else nn.Identity()

        # positional bias

        self.pos_bias = nn.Embedding(fmap_size * fmap_size, heads)

        q_range = torch.arange(fmap_size)
        k_range = torch.arange(fmap_size)

        q_pos = torch.stack(torch.meshgrid(q_range, q_range, indexing = 'ij'), dim = -1)
        k_pos = torch.stack(torch.meshgrid(k_range, k_range, indexing = 'ij'), dim = -1)

        q_pos, k_pos = map(lambda t: rearrange(t, 'i j c -> (i j) c'), (q_pos, k_pos))
        rel_pos = (q_pos[:, None, ...] - k_pos[None, :, ...]).abs()

        x_rel, y_rel = rel_pos.unbind(dim = -1)
        pos_indices = (x_rel * fmap_size) + y_rel

        self.register_buffer('pos_indices', pos_indices)

    def apply_pos_bias(self, fmap):
        bias = self.pos_bias(self.pos_indices)
        bias = rearrange(bias, 'i j h -> () h i j')
        return fmap + (bias / self.scale)

    def forward(self, x):
        qkv = self.to_qkv(x).chunk(3, dim = -1)
        q, k, v = map(lambda t: rearrange(t, 'b n (h d) -> b h n d', h = self.heads), qkv)

        dots = torch.matmul(q, k.transpose(-1, -2)) * self.scale

        # 引入相对位置编码
        dots = self.apply_pos_bias(dots)

        attn = self.attend(dots)
        attn = self.dropout(attn)

        out = torch.matmul(attn, v)
        out = rearrange(out, 'b h n d -> b n (h d)')
        return self.to_out(out)

(4) DeBERTa式

在DeBERTa模型中，移除了值向量的位置编码$p_j$以及注意力计算中的位置-位置注意力项($p_i,p_j$)，并将注意力计算中$x_i,x_j$的位置编码$p_i,p_j$替换为相对位置向量$R_{j,i},R_{i,j}$：

\[\begin{aligned} \alpha_{ij} &= \text{softmax}\{ x_iW^Q (W^K)^T x_j^T+x_iW^Q (W^K)^T R_{i,j}^T+R_{j,i}W^Q (W^K)^T x_j^T \} \\ z_i &= \sum_{j=1}^{n} \alpha_{ij}x_jW^V \end{aligned}\]

(5) Universal RPE (URPE)

注意到在相对位置编码中，如果移除值向量的位置编码$p_j$，会使模型失去通用函数近似的能力。通用相对位置编码(Universal RPE)引入如下约束：

\[z_i = \sum_{j=1}^{n} \alpha_{ij}c_{ij}x_jW^V\]

其中$C=[c_{ij}]$是一个可训练的Toeplitz矩阵: $c_{ij}=g(i−j)$，它与Attention矩阵逐位相乘。尽管这使得Attention矩阵不再是按行的概率矩阵，但恢复了模型的通用近似性。

⚪ 参考文献