SMPL:一种蒙皮多人线性模型.
- paper:SMPL: A Skinned Multi-Person Linear Model
- code:github
- website:link
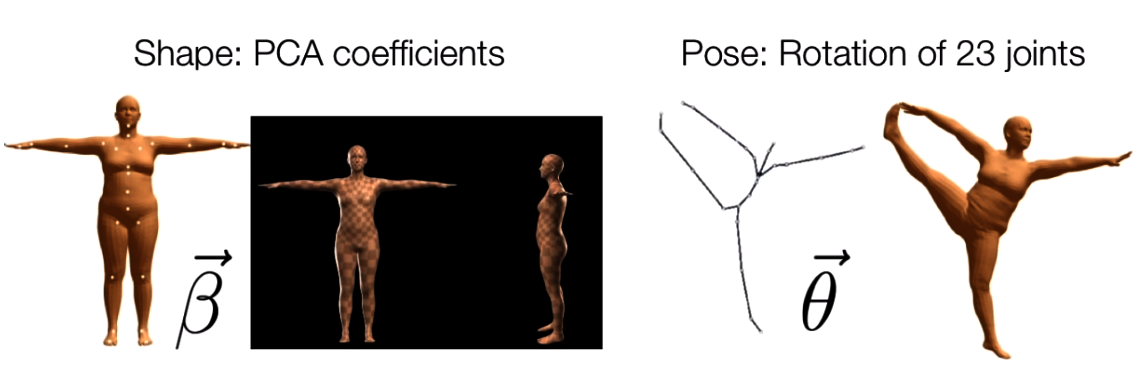
三维人体模型通常有两种表达形式,如下图所示。第一种形式通常用人体关节点(joint)建立的铰链结构表示,这种表示侧重于描述人体的姿态。第二种形式用3D mesh建模人体的蒙皮,这种表示具有更多细节,能够体现人体的形态特征。

SMPL(Skinned Multi-Person Linear Model)是一种通过参数控制的三维人体统计模型,它将人体编码为两类参数:Pose参数$\theta$和Shape参数$\beta$。
- Pose参数$\theta$是一个具有$24 \times 3$个标量值的姿态向量(定义$K=24$个关节点,并建立一组关节点树),该参数代表每个关节点相对于其父节点的局部旋转向量的轴角式表达,用于控制人体姿态变化;
- Shape参数$\beta$是一个具有$10$个标量值的形状向量,其每一维度都可看做人体形状的某个指标,用于控制人体形状变化。
SMPL模型的输出是一个3D mesh,包含$6890$个顶点(vertex)和其构成的$13776$个面元。SMPL模型建立的关节点运动学树(Kinematic Tree)如下图所示:

使用SMPL模型合成一个人体实例的过程包含三步,即形状混合成形(Shape Blend Shapes)、姿态混合成形(Pose Blend Shapes)、蒙皮(Skinning)。
1. 形状混合成形 Shape Blend Shapes
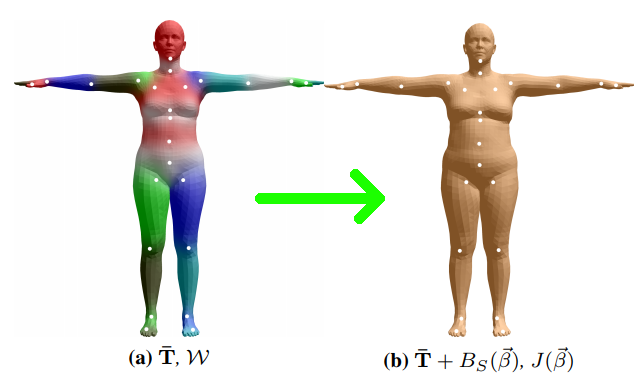
在这一阶段,首先建立在已有数据集上的人体平均模板$\overline{T}$,这个模板是经过统计得到的,认为其具有人体平均姿态和形状。使用形状参数$\beta$描述实际人体形状和模板形状之间的偏移量,通过线性矩阵相乘得到$B_S(\beta)$叠加到原始模板上,得到静默姿态(rest pose,T-pose),即只考虑形状、未考虑姿态的人体mesh。
人体平均模板$\overline{T} \in \Bbb{R}^{6890 \times 3}$建模为包含$6890$个顶点(vertex)的3D mesh。这一步是通过形状主成分(Principal Shape Components,也叫形状PCA基)计算这些顶点的偏移量,并叠加到平均模板上得到静默姿态。形状主成分$S \in \Bbb{R}^{10 \times 6890 \times 3}$是在数据集中学习得到的,用$10$个维度描述人体形状的不同变化程度。这些主成分具有一定的视觉可解释性,其前两个维度的主成分变化可视化如下,第一个维度控制人的高矮,第二个维度控制人的胖瘦:
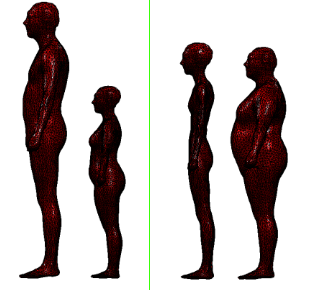
通过对形状参数$\beta \in \Bbb{R}^{10}$进行线性加权计算偏移量:
\[B_S(\beta;S) = \sum_{n=1}^{|\beta|} \beta_n S_n\]2. 姿态混合成形 Pose Blend Shapes
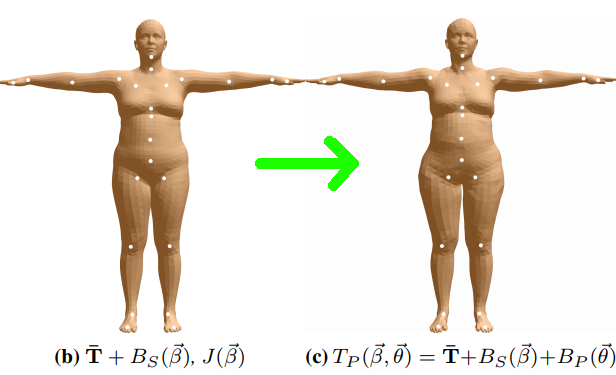
由于人体姿态也会对人体形状产生一定的影响,在这一阶段使用姿态参数$\theta$描述实际人体形状和静默姿态形状之间的偏移量,通过线性矩阵相乘得到$B_P(\theta)$叠加到静默姿态上。
预见建立的人体运动学树保证了子节点和父节点的相对运动关系。以$0$号节点为根节点,通过其他$23$个节点相对于其父节点的旋转角度可以推算整个人体姿态。旋转使用三元数的轴角表达式$\theta = (x,y,z)$,其旋转轴为单位向量\(e=\frac{\theta}{\| \theta \|}\),旋转大小是\(\| \theta \|\)。
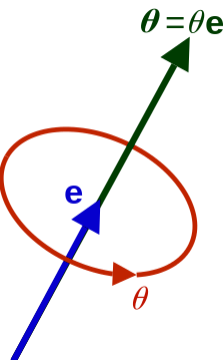
表示这些节点相对于父节点的相对旋转需要用到$23 \times 3$个参数。为了表示人体的全局朝向和空间位置,还需要定义根节点的旋转参数,因此姿态参数$\theta$共有$24 \times 3$个参数。值得一提的是,轴角式的计算并不方便,通常将其转化成旋转矩阵,参数量从$3$变成$9$,具体过程由Rodrigues公式表示:
\[exp(w_j) = I+\hat{w}_j sin(|| w_j ||)+\hat{w}_j^2 cos(|| w_j ||)\]在这一步骤中,只计算人体姿态对形状的影响,而人体的朝向和空间位置不影响混合成形的效果,因此姿态混合成形需要$23 \times 3 =207$个参数。用$R(\cdot)$表示将轴角式转化成旋转矩阵的函数,则由人体姿态导致的人体形状偏移量计算如下:
\[B_P(\theta;P) = \sum_{n=1}^{9K} (R_n(\theta)-R_n(\theta^*)) P_n\]其中姿态主成分(也叫姿态PCA基)$P = [P_1,…,P_{9K}] \in \Bbb{R}^{3N \times 9K} = \Bbb{R}^{3 \times 6890 \times 9 \times 23}$也是在数据集中学习得到的。
3. 蒙皮 Skinning
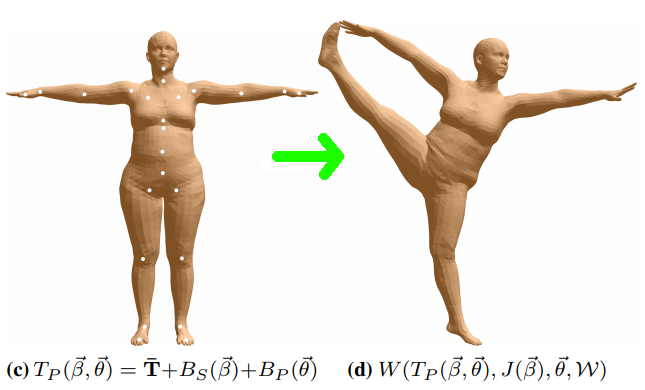
在这一阶段,需要考虑人体姿态的影响。蒙皮的过程是mesh顶点根据关节点的运动变化而产生的加权线性组合。关节点的运动变化是用姿态参数$\theta$描述的,其记录了每个关节点相对于其父节点的相对旋转参数,可以由前向动力学推算所有节点。根据各关节点的理想位置及其相对旋转,便可以得到最终的人体mesh。
每个关节点的理想位置可以由静默姿态下其邻近的mesh顶点加权线性组合得到,其中变换矩阵$\mathcal{J} \in \Bbb{R}^{24 \times 6890}$也是从数据集中学习得到的。这一步计算依赖于形状混合成形后的静默姿态$\overline{T}+B_S(\beta;S) \in \Bbb{R}^{6890 \times 3}$,计算得到的关节点坐标$J(\beta;\mathcal{J},\overline{T},S) \in \Bbb{R}^{24 \times 3}$如下:
\[J(\beta;\mathcal{J},\overline{T},S) = \mathcal{J}(\overline{T}+B_S(\beta;S))\]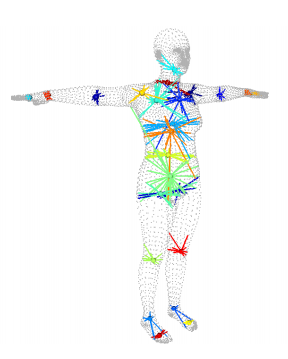
最终得到的SMPL模型函数$M$表达如下:
\[M(\beta, \theta) = W(T_P(\beta, \theta), J(\beta), \theta, \mathcal{W})\]它根据蒙皮模板$T_P$、理想关节点坐标$J$、Pose参数$\theta$和混合权重$\mathcal{W}$计算输出mesh;其中$W$是标准线性蒙皮函数,混合权重$\mathcal{W}$是通过模型训练得到的。其中蒙皮模板$T_P$计算如下:
\[T_P(\beta, \theta) = \overline{T} + B_S(\beta) + B_P(\theta)\]⚪ STAR
- paper:STAR: Sparse Trained Articulated Human Body Regressor
- code:github
- website:link
STAR(Sparse Trained Articulated Human Body Regressor)模型是对SMPL模型的改进,其模型计算过程不变,主要改进在于:
- 姿态PCA基从$207$个减少为$93$个,其具有稀疏性,能减少模型计算时间,使模型更加轻量级;
- 训练数据从$4000$个增加到$14000$个,泛化能力更强,模型的表达能力更强。


