Partition-based Clustering.

基于划分的聚类算法通常需要预先指定簇类的数目或者聚类中心，通过反复迭代，直至最后达到”簇内的点足够近，簇间的点足够远”的目标。

1. K-means算法

（1）K-Means算法的流程

假设共有$N$个样本点$x_1,…,x_N$，需要将其划分为$K$类。记每一类的聚类中心（cluster centroid）为$μ_1,…,μ_K$。

定义失真函数（distortion function）(也叫畸变函数)，用来选择合适的聚类中心以及对每个样本进行正确的分类:

\[J = \frac{1}{N} \sum_{n=1}^{N} {\sum_{k=1}^{K} {[x_n \in k](x_n-μ_k)^2}}\]

这是一个组合优化问题，采用交替优化的方法：

该算法还需要选择初始聚类中心，可随机选择其中$K$个样本。

（2）K-Means算法的图示

  1. 随机选择$k$个初始聚类中心；
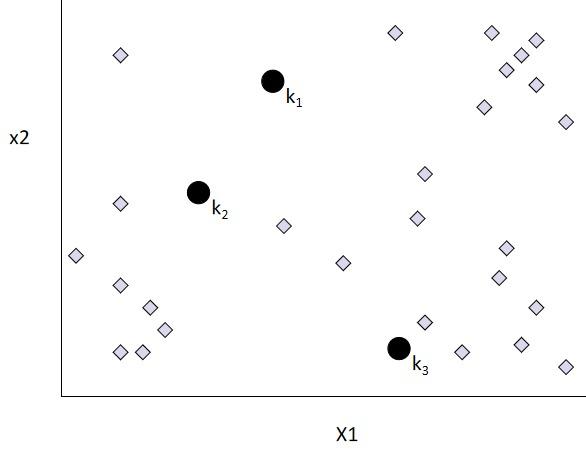
  2. 把每个样本点划分到与其最近的聚类中心所属的类别；
  3. 更新聚类中心为每一个聚类的均值：
  4. 重复步骤$2$和$3$，直至数据的划分不再变化。

（3）K-Means算法的缺点

  1. K-Means需要预先给定类别数$K$，可用肘部法则（elbow method）选定。即根据不同的$K$画出失真函数曲线$J$,选取“肘部”的$K$作为最终的类别数：
  2. 由于采用交替优化的方法，容易陷入局部最优；选择初始聚类中心对结果影响较大；为防止陷入局部极小值，K-Means常循环进行$50$至$1000$次，选择其中失真函数$J$最小的结果：
  3. 需要多次遍历样本集合，计算复杂度高；
  4. 只能找到类球形的类，不能发现任意的类；
  5. 对异常数据敏感。

（4）K-Means算法的实现

from sklearn.cluster import KMeans

kmeans = KMeans(n_clusters=2, random_state=0, n_init="auto").fit(X)
kmeans.labels_
# array([1, 1, 1, 0, 0, 0], dtype=int32)
kmeans.cluster_centers_
# array([[10.,  2.], [ 1.,  2.]])

2. K-means++算法

k-means++是针对k-means中初始质心点选取的优化算法。该算法的流程和k-means类似，改变的地方只有初始质心的选取，该部分的算法流程如下:

  1. 随机选取一个数据点作为初始聚类中心；
  2. 计算每个数据点与当前已有聚类中心的最短距离，距离越大，被选取为下一个聚类中心的概率越大；
  3. 使用轮盘法选取下一个聚类中心，直至聚类中心数量足够。

sklearn.cluster.KMeans默认采用k-means++（init='k-means++'）。

3. Bisecting K-means算法

Bisecting K-means算法是针对kmeans算法会陷入局部最优的缺陷进行的改进算法，该算法基于SSE最小化的原理。SSE(Sum of Squared Error) 表示聚类后的簇中的所有点到该簇的聚类中心距离的平方和，SSE越小，表示聚类效果越好。

Bisecting K-means算法先将所有的数据点视为一个簇，然后通过K-means算法（$k=2$）将该簇一分为二，之后选择其中一个簇继续进行迭代划分；选择哪一个簇进行划分取决于对其划分是否能最大程度的降低SSE的值。

from sklearn.cluster import BisectingKMeans

bisect_means = BisectingKMeans(n_clusters=3, random_state=0).fit(X)
bisect_means.labels_
# array([1, 1, 1, 0, 0, 0], dtype=int32)
bisect_means.cluster_centers_
# array([[10.,  2.], [ 1.,  2.]])

4. K-medoids算法

K-Means与K-Medoids算法过程类似，主要区别在于：

K-Medoids算法对outlier不敏感。