Network Compression.

深度学习模型需要部署到资源受限的设备(resource-limited devices)上，因此需要进行网络压缩(network compression)。

本文目录：

1. Network Pruning
2. Knowledge Distillation
3. Parameter Quantization
4. Architecture Design
5. Dynamic Computation

1. Network Pruning

网络剪枝(Network Pruning)是指把训练好的模型权重weight或神经元neuron丢弃一部分，减小模型的大小而几乎不影响结果。

为什么要进行剪枝？

由于神经网络的复杂性和强大的拟合能力，训练得到的模型通常是过参数化(over-parameterized)的。

为什么不直接训练一个较小的模型呢？通过实验发现，较大模型比较小模型更容易优化。

Lottery Ticket Hypothesis指出，训练好的大模型包括若干最优的子模型，并且通过实验证明了：

• 权重剪枝后的小模型，若随机初始化重新训练，很难达到原来的精度；
• 权重剪枝后的小模型，若使用训练大模型时对应的随机初始化参数，经过相近数量的训练，能够达到原来的精度。

值得注意的是，该理论基于很小的学习率，即模型权重在训练前后的大小相差不是太大。

也有实验证明，剪枝主要学习到的是模型的结构，直接训练小模型也可以达到这个精度；剪枝的重要性还有待进一步研究。

如何剪枝？

对于一个训练好的网络模型，评估其中每个权重weight或神经元neuron的重要性，移除其中一些，之后在训练集上fine-tuning。

权重剪枝和神经元剪枝的区别在于：

• 权重剪枝不改变原始的权重矩阵形状，只是使其变得稀疏；
• 神经元剪枝每剪掉一个神经元，相当于删除权重矩阵的一列，会使权重矩阵形状变小。

1. Weight pruning

权重weight的重要性用其范数衡量，即越接近0的权重越不重要。

由于权重剪枝后的网络结构不规则，很难实现和加速；通常直接把对应权重位置设为$0$实现。

2. Neuron pruning

神经元剪枝容易实现、容易加速。

• 通常$pruning$之后，准确率会有下降，只要下降在可接受的范围内即可；
• 一次不要剪枝太多，否则网络很难通过fine-tuning恢复性能。

神经元剪枝的主要问题在于如何评估神经元neuron的重要性，并根据重要性进行剪枝。衡量神经元重要性的方法包括：

• 用其在给定数据集上的激活次数（非$0$次数）衡量。
• 用该神经元所对应权重的$L1$范数之和作为其重要性，将范数和较小的权重剪掉。
• FPGM（Feature Pruning by Geometric Media）：将范数和划归为几个几何中心，把其余范数和对应神经元剪掉。
• Network Slimming,用batchnorm layer的resize因子$𝛾$來決定神经元的重要性,通常在损失函数上加上对$𝛾$的$L1$范数正则化，使大多数不重要的$𝛾$接近$0$。
• APoZ（Avg % of Zeros）：用该神经元非零值所占的百分比。

2. Knowledge Distillation

• paper

知识蒸馏(knowledge distillation，KD)是指对于一个训练好的较大的teacher net，训练一个较小的student net去拟合teacher net的输出(分布)：

通常较大的网络不仅能获得正确的结果，还能提供更多的信息：如与正确结果相近的结果可能性会高一些。知识蒸馏可以让student net学习到teacher net挖掘的信息。

应用

知识蒸馏的一个典型应用是，在训练时使用Ensemble集成了很多模型，在部署时使用这些大量的复杂模型是不现实的；通过知识蒸馏训练一个student net，使模型轻量化：

方法

知识蒸馏的两种方法：

• Logit Distillation：学生网络学习教师网络的logit输出值
• Feature Distillation：学生网络学习教师网络的feature中间值
• Relational Distillation：学生网络学习样本之间的关系

(1)Logit Distillation

在进行知识蒸馏时，student net学习teacher net经过$softmax$的输出分布；具体地实现方法包括：

1. Baseline KD
2. Deep Mutual Learning
3. Born Again Neural Networks
4. TAKD

1. Baseline KD

学生网络同时学习教师网络的软输出（soft target）和标签的硬输出（hard target）：

通常希望teacher net能够挖掘更多的信息，因此每一个类别的预测概率相差不要太大，引入temperature $T$，防止软输出非常接近硬输出：

则训练的损失函数包括：

• 最小化学生网络和教师网络经过温度调整的输出分布的KL散度；
• 最小化学生网络输出与标签值的交叉熵。

2. Deep Mutual Learning

• paper：Deep Mutual Learning

相互学习（Mutual Learning）的思想是同时训练两个网络，每个网络从另一个网络以及标签中进行学习。

3. Born Again Neural Networks

重生网络的思想是先用Baseline KD的方法训练一个学生网络，在由学生网络迭代地根据交叉熵损失训练若干个学生网络，并将它们集成起来：

4. TAKD

教师网络和学生网络之间的能力差距过大，将导致学生网络无法学习。TAKD用一个参数量介于教师网络和学生网络之间的teacher assistant网络，避免两个网络差距过大：

(2)Feature Distillation

有时教师网络的输出具有很强的语义特征，直接让学生网络学习教师网络的输出是很困难的。Feature Distillation是让学生网络学习教师网络的中间特征。具体地实现方法包括：

1. FitNet
2. Attention

1. FitNet

FitNet先让学生网络的中间层（经过尺寸调整后）学习教师网络的某个中间层特征：

再使用Baseline KD对学生网络进行调整：

由于教师网络和学生网络的模型容量不同、教师网络中可能存在冗余，当两个网络结构差别较大时，该方法效果不好。

2. Attention

将注意力机制引入知识蒸馏，即先将教师网络和学生网络的中间层特征通过注意力压缩，让学生网络学习压缩后的特征。

一种实现方法是对教师网络和学生网络的中间特征沿通道方向平方后相加：

(3)Relational Distillation

逻辑蒸馏和特征蒸馏都是以单个样本为单位训练学生网络学习教师网络，而关系蒸馏是让学生网络学习样本之间的关系：

具体地实现方法包括：

1. Distance-wise & Angle-wise KD
2. Similarity-Preserving KD

1. Distance-wise & Angle-wise KD

对于每一批量的数据，使用教师网络得到他们的输出；学生网络学习这些输出的关系。具体地，可以学习它们的距离关系或夹角关系（用余弦相似度表示）。

2. Similarity-Preserving KD

对于每一批量的数据，使用教师网络得到其中的中间层特征；对这些样本的中间层特征计算余弦相似度，得到余弦相似度表格；训练学生网络学习相似度表格：

3. Parameter Quantization

参数量化(Parameter Quantization)通过量化参数压缩模型，常用的方法如下：

1. 用更少的$bits$表示数值；
2. weight clustering：将权重进行聚类，用聚类中心值代替属于该类的权重值；
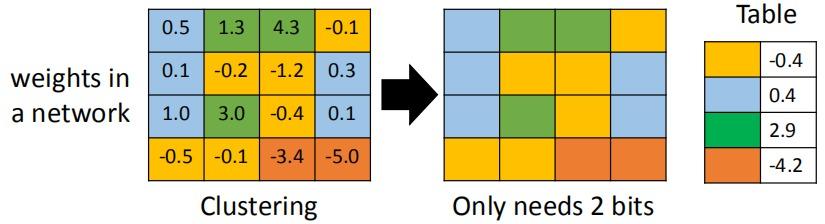
3. Huffman Encoding：用更少的$bits$表示频繁出现的聚类类别，用更多的$bits$表示不频繁出现的类别；
4. Binary Weights：权重取值\(\{-1,+1\}\)，几种典型的方法：

• Binary Connect：paper，使用二值参数空间的梯度近似代替实际梯度方向：
• Binary Network：paper
• XNOR-net：paper

4. Architecture Design

通过设计特殊的网络结构减小参数。

前馈神经网络：Low rank approximation

对于神经元数量为$N$和$M$的两层，权重矩阵\(W \in \Bbb{R}^{M×N}\)；

若在两层中间引入一个线性层，具有$K$个神经元，把权重矩阵分解为\(U \in \Bbb{R}^{M×K}\)和\(V \in \Bbb{R}^{K×N}\)；

则之前的权重总数是$MN$，之后的权重总数是$(M+N)×K$，实现了参数压缩；

但是矩阵$U$和$V$的秩小于等于$W$，一定程度上损失了信息。

卷积神经网络：Depthwise Separable Convolution

深度可分离卷积(depthwise separable convolution)将卷积运算分解成depthwise convolution和pointwise convolution两步。

1. depthwise convolution

depthwise卷积的滤波器数量等于输入通道数量，每一个滤波器只考虑一个通道，通道之间没有影响。

2. pointwise convolution

pointwise卷积使用1×1卷积，仅仅考虑通道间的信息：

对于一个具有$I$个输入通道，$O$个输出通道的网络，设卷积核尺寸为$k×k$，

• 对于常规的卷积，需要参数$(k×k×I)×O$；
• 对于深度可分离卷积，需要参数$(k×k×I)+(I×O)$；

参数量的比值为：\(\frac{(k×k×I)+(I×O)}{(k×k×I)×O} = \frac{1}{O} + \frac{1}{k×k}\)

通常$O$比较大，则深度可分离卷积的参数量大约是常规卷积的\(\frac{1}{k×k}\)。

5. Dynamic Computation

动态计算(Dynamic Computation)是指根据计算环境（如电量）自动调整网络的消耗。

实现方法：

• 训练多个不同大小的网络，环境好时使用大网络，环境差时使用小网络；
• 在网络中间层设置一些分类器，环境好时使用深层的分类器，环境差时使用浅层的分类器；

在浅层加分类器训练时会影响深层的分类精度，一种解决方法是Multi-Scale Dense Networks(MSDN).