Leetcode Exercise Guidence via Python.
本文目录:
零、在线编程常见输入输出练习
一、算法篇
- 贪心算法:分配问题、区间问题
- 双指针:搜索、滑动窗口、快慢指针
- 排序算法
- 二分查找
- 搜索算法:深度优先搜索、回溯法、广度优先搜索
- 动态规划:一维动态规划、二维动态规划、分割问题、并行状态问题、背包问题、股票问题、树形动态规划问题
- 分治法
- 位运算
- 数学问题:模拟求和、数论、几何、随机采样、脑筋急转弯
二、数据结构篇
零、在线编程常见输入输出练习
编程题分两种考核方式:
- 核心代码模式:只需要实现函数核心功能并返回结果,无须处理输入输出;
- ACM模式:按照题目输入输出说明和例题给出的输入输出规范处理输入输出,不同的语言有不同的输入输出规范。
本文介绍ACM模式中常用的输入输出写法(以python语言为例)。
⚪ 输入写法
(1) 输入单行
# 接收一个字符串输入
line = input()
# 接收一个整数输入
line = int(input())
# 接收一组字符串输入(空格隔开)
line = input().split(' ')
# 接收一组整数输入(空格隔开)
line = list(map(int, input().split(' ')))
(2) 输入多行
# 接收固定长度的输入,第一次输入为行数
n = int(input())
for _ in range(n):
line = input()
# 接收不定长度的输入(使用异常处理机制)
while True:
try:
lint = input()
except EOFError:
break
# 接收不定长度的输入(使用系统库)
import sys
for line in sys.stdin:
line = line.strip() # 删除结尾换行符
pass
⚪ 输出写法
(1) 输出单行
# 输出一个元素
print(x)
# 输出一行字符串(空格隔开)
print(' '.join(alist))
# 或
for a in alist:
print(a, end=' ')
一、算法篇
⚪ 贪心算法
贪心算法(又称贪婪算法)是指通过选择当前状态下局部最优的操作来获得全局最优的算法。贪心算法不一定能得到全局最优解,能用贪心算法解决的问题需要满足以下条件:
- 最优子结构:规模较大的问题的解由规模较小的子问题的解组成,规模较大的问题的解只由其中一个规模较小的子问题的解决定;
- 无后效性:后面阶段的求解不会修改前面阶段已经计算好的结果;
- 贪心选择性质:从局部最优解可以得到全局最优解。
(1) 分配问题
分配问题是指以一维数组的形式给出一系列物体,要求为每个物体分配一个属性,且每个物体的属性受到其左右物体的约束;这种约束形式可能是预先指定的,也可能是通过排序施加的。
| 题目 | 题干 | 解法 |
|---|---|---|
| 122. 买卖股票的最佳时机 II medium |
给一个整数数组表示某支股票每天的价格。每天可以决定是否购买和/或出售股票,返回能获得的最大利润。 | 贪心遍历每天的价格,如果价格上涨则卖出并重新购入;否则前一天就卖出。 |
| 135. 分发糖果 easy |
给n个具有不同评分的孩子分发糖果,相邻的孩子评分更高者获得更多糖果,求最少糖果数。 | 使用贪心左右各遍历一遍,每次遍历中只更新相邻一侧的糖果数量关系。 |
| 406. 根据身高重建队列 medium |
给定一个打乱的队列,每个人用身高$h_i$和队列前面身高大于或等于自身的人数$k_i$表示,返回未打乱的队列。 | 按身高倒序排列后贪心地按照位置$k_i$插入新列表,相同身高的人优先插入$k_i$较小者。 |
| 455. 分发饼干 hard |
给定n个具有胃口值的孩子和m个具有尺寸的饼干,求最多满足的孩子数量。 | 饼干和孩子从小到大排序,优先给未满足孩子中最小胃口值的孩子。 |
| 605. 种花问题 easy |
在有一部分空地的花坛中种花,花不能种植在相邻的地块上,求最多能种多少花。 | 遍历时贪心地在左右都是空地的地块上种花。 |
| 665. 非递减数列 medium |
给定一个整数数组,判断在最多改变1个元素的情况下,该数组能否变成一个非递减数列。 | 遍历时贪心地改变不满足条件的两个元素($a_i>a_{i+1}$)其中一个,再判断后续是否满足条件。 |
| 849. 到最近的人的最大距离 medium |
给定一个表示一排座位的数组(0代表座位是空的,1代表有人坐),亚历克斯希望坐在一个能够使他与离他最近的人之间的距离达到最大化的座位上,返回他到离他最近的人的最大距离。 | 对于两侧的连续$k$个空位,最大距离为$k$;对于中间的连续$k$个空位,最大距离为$(k+1)//2$。 |
| 2178. 拆分成最多数目的正偶数之和 medium |
给定一个整数,将它拆分成若干个互不相同的正偶数之和,且拆分出来的正偶数数目最多。 | 只有偶数可以进行拆分,从最小的偶整数2开始依次尝试拆分,直到剩余的数值小于等于当前被拆分的最大偶整数为止。如果此时拆分后剩余值大于零,则将这个数值加到最大的偶整数上。 |
| 2611. 老鼠和奶酪 medium |
有两只老鼠和n块不同类型的奶酪。给定两个正整数数组分别表示第一只老鼠和第二只老鼠吃掉该奶酪的得分。返回第一只老鼠恰好吃掉k块奶酪的情况下,最大得分为多少。 | 对两个得分数组的差值数组降序排列,第一只老鼠吃掉排序后的前k块奶酪。 |
(2) 区间问题
区间问题是指给定一系列区间,通过判断区间是否重叠来解决问题。
若按照区间的左端点进行排序,则可以求得所有重叠区间的并集。反之若按照区间的右端点进行排序,则可以求得所有重叠区间的交集。上述两种过程都可以通过判断当前左端点是否超过记录的右端点来实现:
n = len(alist)
# 按照左端点排序,求并集
alist.sort(key = lambda x: x[0])
ans = []
l, r = alist[0][0], alist[0][1]
for i in range(1, n):
if alist[i][0] > r: # 区间没有重叠
ans.append([l, r])
l, r = alist[i][0], alist[i][1]
else: #区间重叠
r = max(r, alist[i][1])
ans.append([l, r])
# 按照右端点排序,求交集
alist.sort(key = lambda x: x[1])
l, r = alist[0][0], alist[0][1]
for i in range(1, n):
if alist[i][0] >= r: # 区间没有重叠
ans.append([l, r])
l, r = alist[i][0], alist[i][1]
else: #区间重叠
l = max(l, alist[i][0])
ans.append([l, r])
| 题目 | 题干 | 解法 |
|---|---|---|
| 57. 插入区间 medium |
给定一个无重叠的按照区间起始端点排序的区间列表。在列表中插入一个新的区间,需要确保列表中的区间仍然有序且不重叠(如果有必要的话,可以合并区间)。 | 区间已排好序,贪心地合并并插入对应位置即可。 |
| 435. 无重叠区间 medium |
返回需要移除区间集合中的最小区间数量,使剩余区间互不重叠。 | 将区间按照右端点排序,优先保留重叠区间中右端数值较小的区间。 |
| 452. 用最少数量的箭引爆气球 medium |
给定n个可能有重叠的气球,返回引爆所有气球所必须射出的最小弓箭数。 | 将区间按照右端点排序,合并所有具有交集的气球。 |
| 646. 最长数对链 medium |
给定一个数对数组,构造数对链:当且仅当$b < c$时,数对$p2 = [c, d]$才可以跟在$p1 = [a, b]$后面。找出能够形成的最长数对链的长度。 | 将区间按照右端点排序,统计无重叠区间的数量。 |
| 763. 划分字母区间 medium |
给定一个字符串,把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。 | 首先统计每个字母首次和最后出现的区间;将区间按照左端点排序,计算所有重叠区间的并集。 |
⚪ 双指针
双指针算法是指用两个指针变量在线性结构上遍历而解决问题。常见的情况包括:
- 搜索:两个指针指向同一数组,遍历方向相同或相反;此时待搜索的数组往往是排好序的。
- 滑动窗口:两个指针指向同一数组,遍历方向相同且不会相交;此时两个指针包围的区域即为当前的窗口。
- 快慢指针:两个指针在链表上同向移动而解决问题。
(1) 搜索
在相向遍历的双指针搜索中,一个初始指向最小的元素,即数组最左边,向右遍历;一个初始指向最大的元素,即数组最右边,向左遍历。
l, r = 0, len(alist)-1
while l < r:
if case1:
return
elif case2:
l += 1
else:
r -= 1
| 题目 | 题干 | 解法 |
|---|---|---|
| 11. 盛最多水的容器 medium |
给定一个整数数组表示每条垂线的高度,找出其中的两条线使得它们与$x$轴共同构成的容器可以容纳最多的水。 | 使用双指针反向遍历该数组,每次移动指向数值较小的指针(正确性证明:若移动指向数值较大的指针,则容纳水量一定不会增加)。 |
| 15. 三数之和 medium |
给定一个整数数组,判断是否存在三元组,其数值之和等于给定目标值。答案中不可以包含重复的三元组。 | 对整数数组进行排序后,拆分成一系列两数之和问题,则可以使用双指针进行搜索和去重。 |
| 16. 最接近的三数之和 medium |
给定一个整数数组和一个目标值。从数组中选出三个整数,使它们的和与目标值最接近。 | 解法同“15. 三数之和” |
| 18. 四数之和 medium |
给定一个整数数组,判断是否存在四元组,其数值之和等于给定目标值。答案中不可以包含重复的四元组。 | 对整数数组进行排序后,拆分成一系列“15. 三数之和”问题。 |
| 26. 删除有序数组中的重复项 easy |
给定一个升序排列的数组,原地删除重复出现的元素,使每个元素只出现一次,并返回移除后数组的新长度。 | 左指针指向当前已经处理好的序列的尾部,右指针指向待处理序列的头部。右指针不断向右移动,每次右指针指向不重复的数,则将该数赋值到左指针,同时左指针右移。 |
| 27. 移除元素 easy |
给定一个数组和一个值,原地移除所有数值等于给定值的元素,并返回移除后数组的新长度。 | 左指针指向当前已经处理好的序列的尾部,右指针指向待处理序列的头部。右指针不断向右移动,每次右指针指向不需要移除的数,则将左右指针对应的数交换,同时左指针右移。 |
| 75. 颜色分类 medium |
荷兰国旗问题:对包含三个重复值$0,1,2$的数组进行原地排序。 | 使用双指针同向遍历该数组;使用一个指针交换$0$,使用另一个指针交换$1$。 |
| 88. 合并两个有序数组 easy |
合并两个非递减顺序数组,将结果存储在第一个数组中。 | 使用双指针逆序遍历两个数组,把较大值存储在其中一个(经过扩充的)数组尾部。 |
| 167. 两数之和 II - 输入有序数组 medium |
给定一个非0递减顺序数组,从中找出满足相加之和等于目标数的两个数。 | 使用双指针反向遍历该数组;若两指针指向数字之和小于目标数则右移左指针,反之大于则左移右指针。 |
| 283. 移动零 easy |
给定一个数组,编写一个函数将所有0移动到数组的末尾,同时保持非零元素的相对顺序。 | 左指针指向当前已经处理好的序列的尾部,右指针指向待处理序列的头部。右指针不断向右移动,每次右指针指向非零数,则将左右指针对应的数交换,同时左指针右移。 |
| 633. 平方数之和 medium |
给定一个非负整数$c$,判断是否存在两个整数$a$和$b$使得$a^2 + b^2 = c$。 | 使用双指针反向遍历$[0,\sqrt{c}]$。 |
| 680. 验证回文串 II easy |
给定一个字符串$s$,最多可以从中删除一个字符。判断$s$是否能成为回文字符串。 | 使用双指针反向遍历该字符串,贪心(判断字符串首尾是否相等,是则首位同时往中间移动一个字符;不是则首往中间移动一个字符,或者尾往中间移动一个字符)。 |
| 941. 有效的山脉数组 easy |
判断一个整数数组是否为有效的山脉数组:数组中的数值首先单调递增,再单调递减。 | 使用双指针反向遍历数组,左指针单调递增搜索,右指针单调递减搜索,判断两指针是否能重合在非边界处。 |
| 977. 有序数组的平方 easy |
给定一个按非递减顺序排序的整数数组,返回每个数字的平方组成的新数组,要求也按非递减顺序排序。 | 使用双指针反向遍历数组,依次存储绝对值较大的数字的平方。 |
| 2337. 移动片段得到字符串 medium |
给定两个字符串start和target。每个字符串仅由字符’L’、’R’和空位’_‘组成。片段’L’只有在其左侧直接存在一个空位时才能向左移动,而片段’R’只有在其右侧直接存在一个空位时才能向右移动。判断在移动字符串start中的片段任意次之后能否得到字符串target。 | 使用双指针$i,j$依次指向字符串start和target的有效片段,只有满足两片段相同且’L’($i\geq j$)或’R’($i \leq j$)时才能有效匹配。 |
(2) 滑动窗口
在滑动窗口类型的问题中都会有两个指针,一个用于「延伸」现有窗口的 $r$ 指针,和一个用于「收缩」窗口的 $l$ 指针。在任意时刻,只有一个指针运动,而另一个保持静止。
l, r = 0, 0:
while r < len(alist):
if case1:
r += 1
else:
l += 1
| 题目 | 题干 | 解法 |
|---|---|---|
| 76. 最小覆盖子串 hard |
给定两个字符串$s$,$t$,返回$s$中涵盖$t$所有字符的最小子串。 | 使用滑动窗口遍历$s$,使用哈希字典统计窗口中字符出现的次数,使用整型变量判断窗口中是否包含$t$的所有字符。 |
| 2779. 数组的最大美丽值 medium |
给定一个整数数组和一个非负整数k。数组中的任意元素nums[i]可以被替换为范围 [nums[i] - k, nums[i] + k] 内的任一整数。返回数组的美丽值,定义为数组中由相等元素组成的最长子序列的长度。 | 对数组进行排序,通过滑动窗口寻找最长的区间$[i,j]$,满足$nums[j]-nums[i]\leq 2k$。 |
(3) 快慢指针
快慢指针(Floyd 判圈法)适用于链表找环路的通用解法。给定两个指针,分别命名为 slow 和 fast,起始位置在链表的开头。每次 fast 前进两步,slow 前进一步。如果链表中存在环,则一定存在一个时刻 slow 和 fast 相遇。
设链表中环外部分的长度为 $a$。slow 指针进入环后,又走了 $b$ 的距离与 fast 相遇。此时,fast 指针已经走完了环的 $n$ 圈,因此它走过的总距离为 $a+b+n(b+c)$。
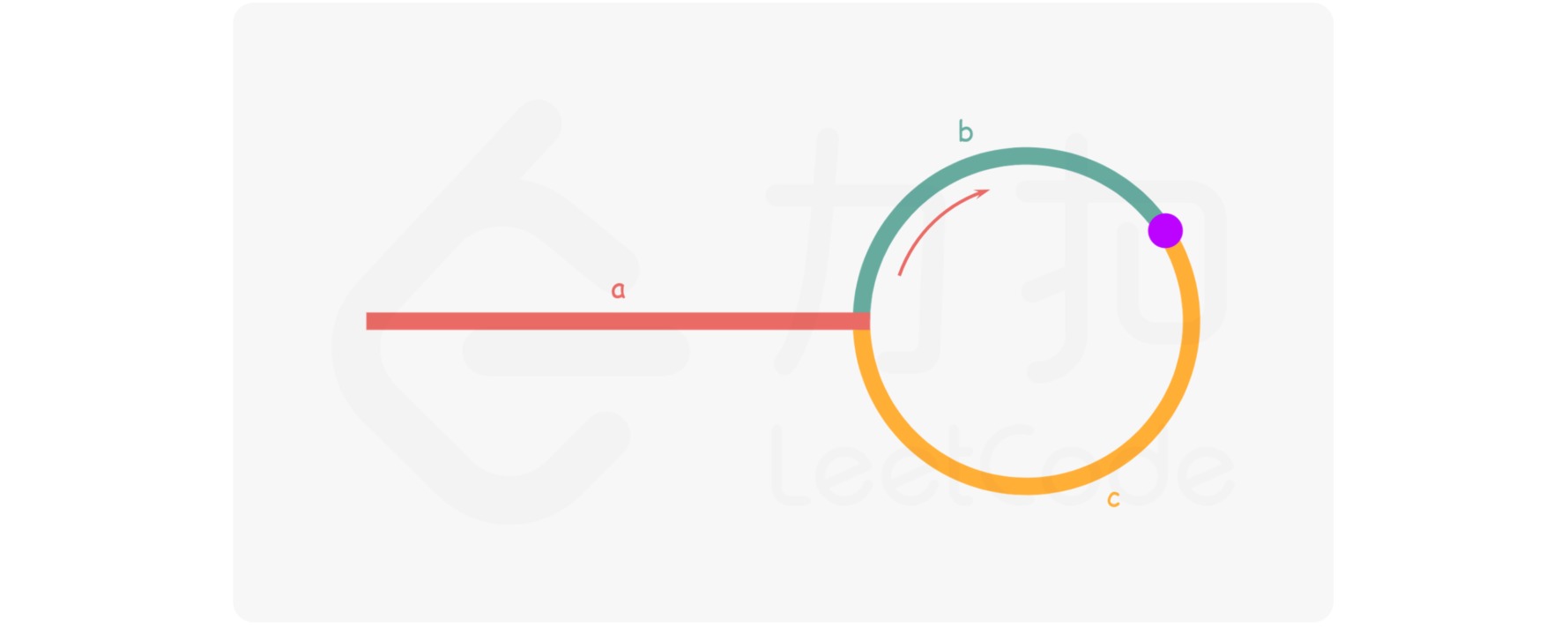
任意时刻,fast 指针走过的距离都为 slow 指针的 $2$ 倍。因此有:
\[a+b+n(b+c) = 2(a+b) \leftrightarrow a = c+(n-1)(b+c)\]即从相遇点到入环点的距离$c$加上 $n-1$ 圈的环长,恰好等于从链表头部到入环点的距离$a$。
因此当 slow 和 fast 第一次相遇时,将 fast 重新移动到链表开头,并让 slow 和 fast 每次都前进一步。最终,它们会在入环点相遇。
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
def detectCycle(head: Optional[ListNode]) -> Optional[ListNode]:
slow, fast = head.next, head.next.next
while slow != fast:
slow = slow.next
fast = fast.next.next
fast = head
while slow != fast:
slow, fast = slow.next, fast.next
return fast
此外快慢指针还可以用于寻找单链表中的第$\frac{n}{k}$个节点($n$是链表长度):慢指针一次走一步,快指针一次走$k$步,快慢指针同时出发。当快指针移动到链表的末尾时,慢指针恰好到链表的第$\frac{n}{k}$个节点。
以寻找链表中间节点($k=2$)为例:
slow, fast = head, head
while fast.next and fast.next.next:
slow = slow.next
fast = fast.next.next
| 题目 | 题干 | 解法 |
|---|---|---|
| 141. 环形链表 easy |
给定一个链表的头节点,判断链表中是否有环。 | 使用快慢指针判断是否有环。 |
| 142. 环形链表 II medium |
给定一个链表的头节点,返回链表开始入环的第一个节点。 | 快慢指针,注意判断无环的情况。 |
| 143. 重排链表 medium |
给定一个单链表L0 → L1 → … → Ln-1 → Ln,将其重新排列为L0 → Ln → L1 → Ln-1 → L2 → Ln-2 → …。 | 先用快慢指针找到链表中点,再将后半列表反转,最后合并两个链表。 |
| 148. 排序链表 medium |
给定链表的头节点,将其按升序排列并返回排序后的链表。 | 利用快慢指针找到链表中点后,可以对链表进行归并排序。 |
| 202. 快乐数 easy |
编写一个算法来判断一个数是不是快乐数。快乐数定义为:对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和;然后重复这个过程直到这个数变为$1$;注意可能无限循环但始终变不到$1$。 | 对于非快乐数,快慢指针会在非$1$处相遇;对于快乐数,快指针会先到达$1$处。 |
| 234. 回文链表 easy |
给定一个单链表的头节点,判断该链表是否为回文链表。 | 先使用快慢指针找到链表中点,再把链表切成两半;然后把后半段翻转;最后比较两半是否相等。 |
⚪ 排序算法
常见的排序算法有:插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。关于这些排序算法的细节介绍请参考Python实现排序算法。

python提供了内置的排序算法:
# 直接排序数组(从小到大)
alist.sort(reverse=False)
alist = sorted(alist)
# 获取排序索引(从小到大)
idx = list(range(len(alist)))
idx.sort(key=lambda i: alist[i])
虽然在python里可以通过alist.sort()快速排序,而且刷题时很少需要自己手写排序算法,但是熟习各种排序算法可以加深对算法的基本理解,以及解出由这些排序算法引申出来的题目。
| 题目 | 题干 | 解法 |
|---|---|---|
| 215. 数组中的第K个最大元素 medium |
返回数组中第$k$个最大的元素。 | 快速选择算法: 只需要找到快速排序中第$k$大的枢即可,不需要对其左右再进行排序。 |
| 347. 前 K 个高频元素 medium |
返回数组中出现频率前$k$高的元素。 | 使用哈希字典存储每个元素出现的次数,并对出现次数应用桶排序。 |
| 451. 根据字符出现频率排序 medium |
给定一个字符串,根据字符出现的频率对其进行降序排序。 | 使用哈希字典存储每个字符出现的次数,并对出现次数应用桶排序。 |
| 912. 排序数组 medium |
给定一个整数数,将该数组升序排列。 | 可以通过该题练习不同的排序算法。 |
⚪ 二分查找
二分查找也常被称为二分法或者折半查找,每次查找时通过将待查找区间分成两部分并只取一部分继续查找,将查找的复杂度大大减少。对于一个长度为 $O(n)$ 的数组,二分查找的时间复杂度为 $O(\log n)$。
二分查找时区间的左右端取开区间还是闭区间在绝大多数时候都可以,尝试熟练使用一种写法,比如左闭右开(满足 C++、Python 等语言的习惯)或左闭右闭(便于处理边界条件);如果某种写法无法跳出死循环,则考虑尝试另一种写法。
二分查找也可以看作双指针的一种特殊情况,但一般会将二者区分。双指针类型的题,指针通常是一步一步移动的;而在二分查找里,指针每次移动半个区间长度。
l, r = 0, n-1
while l <= r:
# mid = (l+r)//2
mid = l+(r-l)//2 # 搜索范围较大时,防止下标越界
if alist[mid] == c:
return True
elif alist[mid] < c:
l = mid + 1
else:
r = mid - 1
可以通过bisect库中的bisect.bisect_left函数实现二分查找。该函数接收一个有序数组和一个目标值,返回大于等于目标值的第一个下标(相当于C++中的lower_bound)。
import bisect
idx = bisect.bisect_left(alist, target)
if idx < len(alist) and alist[idx] == target:
return True
return False
| 题目 | 题干 | 解法 |
|---|---|---|
| 33. 搜索旋转排序数组 medium |
对一个升序排列的不重复整数数组在某个下标上进行旋转,判断给定的目标值是否存在于数组中。 | 二分查找时若不能确定左右区间,则可以判断左端点并简单地将左端点右移一位。 |
| 34. 在排序数组中查找元素的第一个和最后一个位置 medium |
给定一个按照非递减顺序排列的整数数组和一个目标值,找出给定目标值在数组中的开始位置和结束位置。 | 两次二分查找分别搜索起止位置。 |
| 69. x 的平方根 easy |
返回非负整数 $x$ 的算术平方根的整数部分。 | 二分查找区间$[0,x]$。 |
| 81. 搜索旋转排序数组 II medium |
对一个非降序排列的整数数组在某个下标上进行旋转,判断给定的目标值是否存在于数组中。 | 二分查找时若不能确定左右区间,则可以判断左端点并简单地将左端点右移一位。 |
| 153. 寻找旋转排序数组中的最小值 medium |
对一个升序排列的整数数组在某个下标上进行旋转,找出数组中的最小元素。 | 若二分值小于左端值或小于右端值则搜索左区间,否则判断左端点并简单地将左端点右移一位。 |
| 154. 寻找旋转排序数组中的最小值 II hard |
对一个非降序排列的整数数组在某个下标上进行旋转,找出数组中的最小元素。 | 思路同81。 |
| 540. 有序数组中的单一元素 medium |
给定一个仅由整数组成的有序数组,其中每个元素都会出现两次,唯有一个数只会出现一次。找出只出现一次的数。 | 二分查找奇数长度区间。 |
| 1170. 比较字符串最小字母出现频次 medium |
定义一个函数$f(s)$统计$s$中(按字典序比较)最小字母的出现频次。给定两个字符串数组待查表 queries 和词汇表 words。对于每次查询 queries$[i]$ ,统计 words 中满足 $f($queries$[i]) < f(W)$ 的词的数目。 | 首先构造词汇表的最小字母频次数组并排序,对于每次查询,二分查找词汇表中大于查询频次的数量。 |
如果题目中有「最大化最小值」或者「最小化最大值」,一般都是二分查找答案。以最大化最小值类型的题目为例,首先给定最小值可能的存在范围$[left, right]$,每次二分查找中值$mid$;判断在给定题目条件下能否取得该最小值;若能够取得,则还有可能取得更大的值,此时更新$left$;若不能够取得,则只能进一步评估更小的最小值,此时更新$right$。
def MaxMin(alist):
left, right = minVal, maxVal # 设置搜索范围
ans = -1
while left <= right:
mid = left + (right-left)//2
if check(mid, alist): # 若mid能取得
ans = mid
left = mid+1
else:
right = mid-1
return ans
| 题目 | 题干 | 解法 |
|---|---|---|
| 1552. 两球之间的磁力 medium |
给定一个数组代表n个篮子的位置,在两个篮子中分别放两个球,它们之间的磁力为两个位置之差的绝对值。现把m个球放到这些篮子里,使得任意两球间最小磁力最大,返回最大化的最小磁力。 | 二分搜索可能出现的最小磁力(范围是1到最大位置减最小位置)。判断最小磁力能否满足:按照不小于最小磁力的间隔放球,判断能否放够m个球。 |
| 2439. 最小化数组中的最大值 medium |
给定一个非负整数数组,每次可以将当前数值减一(不小于零),同时将前一个数值加一。返回可以得到的数组中最大值最小为多少。 | 二分搜索可能出现的最大值(范围是原数组中的最小值到最大值)。判断最大值能否满足:贪心地把数组的每个值调整到最大值,若当前值小于最大值则从后续数组中借用一些数值,若当前值大于最大值并且完成借用后仍大于最大值,则条件不满足。 |
| 2513. 最小化两个数组中的最大值 medium |
给定两个空数组,往它们中添加正整数,使它们满足:数组1中的整数不能被d1整除,数组2中的整数不能被d2整除,每个整数只能使用一次。给定d1,d2和两个数组的指定长度L1,L2,返回两个数组中最大元素的最小值。 | 二分搜索可能出现的最大元素(范围是L1+L2到2(L1+L2))。判断最大元素$x$能否满足:$\lfloor \frac{x}{d_2}\rfloor - \lfloor \frac{x}{lcm(d_1,d_2)} \rfloor$个元素只属于数组1,$\lfloor \frac{x}{d_1}\rfloor - \lfloor \frac{x}{lcm(d_1,d_2)} \rfloor$个元素只属于数组2,$x-\lfloor \frac{x}{d_1}\rfloor-\lfloor \frac{x}{d_2}\rfloor+\lfloor \frac{x}{lcm(d_1,d_2)} \rfloor$个元素同时属于数组1和数组2。 |
| 2517. 礼盒的最大甜蜜度 medium |
给定不同糖果的价格,组合k类不同糖果打包成礼盒出售。礼盒的甜蜜度是礼盒中任意两种糖果价格绝对差的最小值。返回礼盒的最大甜蜜度。 | 二分搜索可能出现的最大甜蜜度(范围是0到最大价格减最小价格)。判断最大甜蜜度能否满足:按照不小于甜蜜度的间隔选择糖果,判断能否选够k类糖果。 |
| 2560. 打家劫舍 IV medium |
沿街有一排连续的房屋。每间房屋内都藏有一定的现金。一位小偷计划从这些房屋中窃取现金,小偷不会窃取相邻的房屋。小偷的窃取能力定义为他在窃取过程中能从单间房屋中窃取的最大金额,小偷总能窃取至少k间房屋。返回小偷的最小窃取能力。 | 二分搜索小偷的窃取能力(范围在每间房屋的金额)。判断窃取能力$x$能否满足:定义状态$dp[i]$为窃取前$i$个房间时只窃取不超过金额$x$对应的最大房间数,状态转移方程$dp[i]=\max(dp[i-1], dp[i-2]+1),nums[i]\leq x$。判断$dp[n]$能否超过$x$。 |
| 2594. 修车的最少时间 medium |
给定一个整数数组表示一些机械工的能力值。能力值为$r$的机械工可以在$rn^2$分钟内修好$n$辆车。所有机械工可以同时修理汽车,返回修理所有汽车最少需要多少时间。 | 二分搜索修车的时间(范围在能力值最小的人修车的时间之内)。判断修车时间$t$能否满足:所有机械工在时间$t$内修理的车辆总和超过给定车辆数。 |
| 2616. 最小化数对的最大差值 medium |
给定一个整数数组和一个整数p,从数组中找到p个下标对,每个下标对对应数值取差值,使得这p个差值的最大值最小。返回p个下标对对应数值最大差值的最小值。 | 二分搜索可能出现的最大差值(范围是0到数组最大值与最小值之差)。判断最大差值$x$能否满足:数组排序后计算相邻差值矩阵,问题等价于是否能从差值矩阵中选取不相邻的p个数值不大于$x$的元素,采用与“2560. 打家劫舍 IV”相同的动态规划解决。 |
⚪ 搜索算法
(1) 深度优先搜索
深度优先搜索(depth-first search,DFS)在搜索到一个新的节点时,立即对该新节点进行遍历;对于树结构而言,由于总是对新节点调用遍历,因此看起来是向着“深”的方向前进。
DFS遍历需要用先入后出的栈(stack)来实现,也可以通过与栈等价的递归来实现。但因为栈与递归的调用原理相同,而递归相对便于实现,因此刷题时推荐使用递归式写法,同时也方便进行回溯。不过在实际工程上,直接使用栈可能才是最好的选择,一是因为便于理解,二是更不易出现递归栈满的情况。
有时我们可能会需要对已经搜索过的节点进行标记,以防止在遍历时重复搜索某个节点,这种做法叫做状态记录或记忆化(memoization)。
深度优先搜索类型的题可以分为主函数和辅函数,主函数用于遍历所有的搜索位置,判断是否可以开始搜索,如果可以即在辅函数进行搜索。辅函数则负责深度优先搜索的递归调用。
在辅函数内进行递归搜索时,需要注意边界条件的判定。边界判定一般有两种写法,一种是先判定是否越界,只有在合法的情况下才进行下一步搜索(即判断放在调用递归函数前);另一种是先进行下一步搜索,待下一步搜索开始时再判断是否合法(即判断放在辅函数第一行)。
一般地,使用DFS遍历$m \times n$的$0/1$二维数组中所有值为$1$的连通域的写法如下:
def solve(matrix):
m, n = len(matrix), len(matrix[0])
# 状态记录
visited = set()
# 写法①:先判定边界条件再进行搜索
def dfs(i, j):
visited.add((i,j))
for di,dj in [(-1,0), (1,0), (0,-1), (0,1)]:
new_i, new_j = i+di, j+dj
if (0<=new_i<m) and (0<=new_j<n) and (new_i, new_j) not in visited and matrix[new_i][new_j] == 1:
dfs(new_i, new_j)
for i in range(m):
for j in range(n):
if matrix[i][j]==1 and (i, j) not in visited:
dfs(i, j)
# 写法②:先搜索再判定边界条件
def dfs(i, j):
if (i<0 or i>=m) or (j<0 or j>=n) or (i, j) in visited or matrix[i][j] == 0:
return
visited.add((i,j))
for di,dj in [(-1,0), (1,0), (0,-1), (0,1)]:
dfs(i+di, j+dj)
for i in range(m):
for j in range(n):
dfs(i, j)
| 题目 | 题干 | 解法 |
|---|---|---|
| 130. 被围绕的区域 medium |
找到由字符’X’和’O’组成的矩阵中所有被’X’围绕的区域,并将这些区域里所有的’O’用’X’填充。 | 使用深度优先搜索沿矩阵边缘搜索’O’,并填充未被搜索到的’O’。 |
| 200. 岛屿数量 medium |
给定一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,计算网格中岛屿的数量。 | 使用深度优先搜索’1’,并修改与之相邻的’1’。 |
| 417. 太平洋大西洋水流问题 medium |
雨水只能从高向低流,求矩阵中哪些坐标的雨水既可以流入太平洋(左上)又可以流入大西洋(右下)。 | 使用深度优先搜索实现反向搜索,求两次搜索的交集。 |
| 547. 省份数量 medium |
返回矩阵中省份的数量,省份是一组直接或间接相连的城市,组内不含其他没有相连的城市。 | 深度优先搜索,计算图中的连通分量数。 |
| 695. 岛屿的最大面积 medium |
计算最大的岛屿面积,岛屿的面积是岛上值为 $1$ 的单元格的数目,在水平或者竖直的四个方向上相邻。 | 深度优先搜索,在辅函数中记录面积并返回。 |
| 1254. 统计封闭岛屿的数目 medium |
二维矩阵由0(土地)和1(水)组成。岛是由最大的4个方向连通的0组成的群,封闭岛是一个完全由1包围(左、上、右、下)的岛。返回封闭岛屿的数目。 | 使用深度优先搜索沿矩阵边缘搜索0,并统计剩余0的连通域数量。 |
| 2596. 检查骑士巡视方案 medium |
骑士会从棋盘的左上角出发,并且访问棋盘上的每个格子恰好一次。骑士行动时可以垂直移动两个格子且水平移动一个格子,或水平移动两个格子且垂直移动一个格子。判断是否存在有效的巡视方案(按自然数顺序巡视)。 | 使用深度优先搜索按照移动方向依次搜索自然数即可。 |
(2) 回溯法
回溯法(backtracking)是优先搜索的一种特殊情况,又称为试探法,常用于需要记录节点状态的深度优先搜索。通常来说,排列、组合、选择类问题使用回溯法比较方便。
回溯法的核心是回溯。在搜索到某一节点的时候,如果我们发现目前的节点(及其子节点)并不是需求目标时,我们回退到原来的节点继续搜索,并且把在目前节点修改的状态还原。这样的好处是我们可以始终只对图的总状态进行修改,而非每次遍历时新建一个图来储存状态。
在具体的写法上,它与普通的深度优先搜索一样,都有 [修改当前节点状态]→[递归子节点] 的步骤,只是多了回溯的步骤,变成了 [修改当前节点状态]→[递归子节点]→[回改当前节点状态]。
回溯法修改一般有两种情况,一种是修改最后一位输出,比如排列组合;一种是修改访问标记,比如矩阵里搜字符串。回溯法的两个小诀窍:一是按引用传状态,二是所有的状态修改在递归完成后回改。
以全排列的顺序访问$n$个元素的数组nums的写法:
def solve(nums):
n = len(nums)
# 状态记录
visited = set()
def backtrack():
if len(state) == n:
# state所指向的列表在深度优先遍历的过程中只有一份
# 在进行值传递的过程中需要做一次拷贝
res.append(state[:])
return
for j in range(n):
if i not in visited:
# 修改当前节点状态
visited.add(j)
state.append(nums[j])
# 递归子节点
backtrack()
# 回改当前节点状态
visited.remove(j)
state.pop()
for i in range(n):
# 设置初始状态,这一步也可以合并到递归函数中
state = [nums[i]]
visited.add(i)
backtrack()
visited.remove(i)
此外,也可以通过itertools库直接实现数组的排列与组合:
itertools.permutations(alist)
itertools.combinations(alist, k)
| 题目 | 题干 | 解法 |
|---|---|---|
| 17. 电话号码的字母组合 medium |
给定一个仅包含数字2-9的字符串,返回所有它能表示的字母组合。数字到字母的映射与电话按键相同。 | 回溯,状态设置为当前字符位置,使用哈希字典表示每个字符对应的字母。 |
| 37. 解数独 hard |
通过填充空格来解决数独问题。 | 回溯,遍历所有待求解位置,使用标识符判断是否解完。 |
| 40. 组合总和 II medium |
找出集合中所有可以使数字和为目标数的组合。集合中的每个数字在每个组合中只能使用一次。 | 回溯,状态设置为当前和,使用哈希集合统计重复数字以去重。 |
| 46. 全排列 medium |
返回一个不含重复数字的数组的所有可能的全排列。 | 回溯,状态设置为当前数组的长度。 |
| 47. 全排列 II medium |
返回一个可包含重复数字的数组的所有不重复的全排列。 | 回溯,状态设置为当前数组的长度,在同一位置上需要去重。 |
| 51. N 皇后 hard |
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。 | 每个皇后必须位于不同行和不同列。回溯,状态设置为当前行。使用集合记录冲突的列、左斜线(行列下标之和)和右斜线(行列下标之差)。 |
| 77. 组合 medium |
返回范围 $[1, n]$ 中所有可能的 $k$ 个数的组合。 | 回溯,状态设置为当前数组的长度。 |
| 78. 子集 medium |
给定一个整数数组,数组中的元素互不相同。返回该数组所有可能的子集(幂集)。 | 回溯,状态设置为数组的当前搜索位置,分别按使用和不使用该位置的元素搜索两次。 |
| 79. 单词搜索 medium |
给定一个二维字符网格和一个字符串单词,判断单词是否存在于网格中。 | 回溯,状态设置为单词的当前搜索位置。 |
| 980. 不同路径 III hard |
在二维网格上,有4种类型的方格:1表示起始方格;2表示结束方格;0表示可以走过的空方格;-1表示无法跨越的障碍。返回从起始方格到结束方格的不同路径的数目,每一个无障碍方格都要通过且只能通过一次。 | 预先统计应走过的方格数量,回溯所有可能的路径。 |
| 1079. 活字印刷 medium |
有一套活字字模,其中每个字模上都刻有一个字母。返回可以印出的非空字母序列的数目。 | 通过回溯实现包含重复字母的全排列。 |
| 1240. 铺瓷砖 hard |
房子的客厅大小为$n \times m$,需要使用尽可能少的正方形瓷砖来铺盖地面,最少需要用到多少块方形瓷砖? | 从左到右、从上到下依次遍历位置$(i,j)$:若$i$越界表明已铺满;若$j$越界则转到$(i+1,0)$;若$(i,j)$已铺瓷砖则转到$(i,j+1)$;若$(i,j)$未铺瓷砖则依次搜索$r=[\min(n-i,m-j):1]$大小的正方形区域铺瓷砖并转到$(i,j+r)$。剪枝策略:若当前铺瓷砖数已大于历史最少瓷砖数则返回。 |
(3) 广度优先搜索
广度优先搜索(breadth-first search,BFS)不同于深度优先搜索,它是一层层进行遍历的,因此需要用先入先出的队列进行遍历。由于是按层次进行遍历,广度优先搜索时按照“广”的方向进行遍历,也常常用来处理最短路径等问题。
深度优先搜索和广度优先搜索都可以处理可达性问题,即从一个节点开始是否能达到另一个节点。因为深度优先搜索可以利用递归快速实现,很多人会习惯使用深度优先搜索刷此类题目。实际软件工程中很少见到递归的写法,因为一方面难以理解,另一方面可能产生栈溢出的情况;而用栈实现的深度优先搜索和用队列实现的广度优先搜索在写法上并没有太大差异,因此使用哪一种搜索方式需要根据实际的功能需求来判断。
在最短路问题中,如果要求多个源点出发的最短路时,一般我们都会建立一个「超级源点」连向所有的源点,用「超级源点」到终点的最短路等价多个源点到终点的最短路。
一般地,使用BFS遍历$m \times n$的$0/1$二维数组中所有值为$1$的连通域的写法如下:
def solve(matrix):
m, n = len(matrix), len(matrix[0])
# 建立队列
from collections import deque
queue = deque([])
# 状态记录
visited = set()
for i in range(m):
for j in range(n):
if (i,j) not in visited and grid[x][y]==1:
queue.append((i,j))
while queue:
x, y = queue.popleft()
if x<0 or x>=m or y<0 or y>=n or (x,y) in visited:
continue
visited.add((x,y))
for (dx, dy) in [(-1,0), (1,0), (0,-1), (0,1)]:
queue.append((x+dx, y+dy))
| 题目 | 题干 | 解法 |
|---|---|---|
| 310. 最小高度树 medium |
找到一个无向无环图中所有的最小高度树,并按任意顺序返回它们的根节点标签列表。 | 最小高度树的根节点一定是图中的最长路径的中间节点。首先以任意节点$p$出发通过BFS找到最远终点$x$,再从$x$出发找到最远终点$y$,则$x\to y$为最远路径。 |
| 542. 01 矩阵 medium |
给定一个由 0 和 1 组成的矩阵,请输出一个大小相同的矩阵,其中每一个格子是矩阵中对应位置元素到最近的 0 的距离。 | 从所有0元素开始BFS,每找到一个新位置距离加1。 |
| 934. 最短的桥 medium |
求最少要填海造陆($0\to 1$)多少个位置才可以将个二维 0-1 矩阵中两个由1组成的岛屿相连。 | 第一次DFS或BFS搜索第一座岛并记录边缘位置,第二次BFS从边缘位置开始搜索。 |
| 1654. 到家的最少跳跃次数 medium |
有一只跳蚤的家在数轴上的位置x处。帮助它从位置0出发,到达它的家。跳蚤跳跃的规则如下:它可以往前跳a个位置、往后跳b个位置、不能连续往后跳2次、不能跳到forbidden数组中的位置。 | BFS时可以设置一个合理的上界(如$\max(forbidden)+a+b+x$),由于不能连续两次向后跳,在队列中存储上一次跳的方向,并且当向后跳到某个位置时,不记录该位置已访问(因为向前跳到该位置后仍然可以向后跳)。 |
| LCP 41. 黑白翻转棋 medium |
在棋盘中有黑白两种棋子,当落下的棋子与其他相同颜色的棋子在行、列或对角线完全包围(中间不存在空白位置)另一种颜色的棋子,则可以翻转这些棋子的颜色。若下一步可放置一枚黑棋,请问选手最多能翻转多少枚白棋。若翻转白棋成黑棋后,棋盘上仍存在可以翻转的白棋,将可以继续翻转白棋。 | 对每一个空余位置尝试黑棋放置,用一个队列来存储正在进行「翻转操作」的白棋位置,若队列非空,从队列中取出队首元素,进行行、列和对角线 8 个方向判断是否有可以翻转的白棋——判断沿着方向是否是连续的一段白棋并以另一颗黑棋结尾。若有可以翻转的白棋,则将这些白旗进行翻转,并加入队列中。直至队列为空表示一次放置黑棋结束。 |
⚪ 动态规划
动态规划(Dynamic Programming, DP)是将原问题拆成多个重叠子问题进行求解。为了避免重复求解子问题,动态规划保存子问题的解,避免重复计算。动态规划只能应用于有最优子结构的问题,即局部最优解能决定全局最优解。
解决动态规划问题的关键是找到状态转移方程,以便于通过计算和储存子问题的解来求解最终问题。同时也可以对动态规划进行空间压缩,起到节省空间消耗的效果;一种常用的空间压缩方法是滚动数组,相比于直接存储所有的$n$个状态,若状态转移方程中当前状态只与前面$k<n$个状态有关,则只使用$k$个变量来存储之前的状态。
动态规划可以看成是带有状态记录(memoization)的优先搜索。状态记录是指如果一个子问题在优先搜索时已经计算过一次,则可以把它的结果储存下来,之后遍历到该子问题时直接返回储存的结果。
动态规划是自下而上的,即先解决子问题,再解决父问题;而带有状态记录的优先搜索是自上而下的,即从父问题搜索到子问题,若重复搜索到同一个子问题则进行状态记录,防止重复计算。
如果题目需求的是最终状态,那么使用动态规划比较方便;如果题目需要输出所有的路径,那么使用带有状态记录的优先搜索会比较方便。
一般地,动态规划的求解思路:
- 状态定义: $dp[i]$
- 列出转移方程: $dp[i+1] = f(dp[i],dp[i-1],…)$
- 给定边界条件: $dp[0]$
- 返回结果: $dp[n]$
(1) 一维动态规划
以斐波那契数列$f(n)=f(n-1)+f(n-2)$为例,1D DP的写法如下
def dp1D(n):
p0, p1 = 0, 1
for i in range(2, n+1):
p2 = p0 + p1
p0, p1 = p1, p2
return p1
| 题目 | 题干 | 解法 |
|---|---|---|
| 32. 最长有效括号 hard |
给定一个只包括 ‘(‘,’)’的字符串,找出最长有效(格式正确且连续)括号子串的长度。 | 状态定义:$dp[i]$为以第$i$个元素为结尾的最长有效括号长度 转移方程:\(dp[i] = \begin{cases} dp[i-2]+2, & s[i-1]='(', s[i] = ')' \\ dp[i-1] + dp[i-dp[i-1]-2] + 2 , & s[i-1]=s[i] = ')', s[i-dp[i-1]-1]='(' \\ 0, & s[i] = '(' \end{cases}\) 边界条件:\(dp[0]=dp[1]=0\) 返回值:\(\max(dp)\) |
| 42. 接雨水 hard |
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 | 解题思路:每个柱子能接到的雨水量等于两边的最大高度的最小值减去当前高度 状态定义:$leftMax[i]$为下标$i$及其左边位置中的最大高度;$rightMax[i]$为下标$i$及其右边位置中的最大高度 转移方程:\(\begin{aligned} leftMax[i] &= \max(leftMax[i-1], height[i]), i=1:n-1 \\ rightMax[i] &= \max(rightMax[i+1], height[i]), i=n-2:0 \end{aligned}\) 边界条件:\(leftMax[0]=height[0],rightMax[n-1]=height[n-1]\) 返回值:\(\sum_i \min(rightMax[i]-leftMax[i])-height[i]\) |
| 55. 跳跃游戏 medium |
给定一个非负整数数组,数组中的每个元素代表在该位置可以跳跃的最大长度。判断是否能够到达最后一个下标。 | 状态定义:$dp[i]$为以在第$i$个位置可以跳跃的最大长度 转移方程:\(dp[i] = \max(dp[i-1]-1, nums[i])\) 边界条件:\(dp[0]=0\) 返回值:\(dp[i]>0, i \in [1,n)\) 空间压缩:使用长度为1的滚动数组 |
| 70. 爬楼梯 easy |
每次可以爬 1 或 2 个台阶,有多少种不同的方法可以爬到n 阶楼顶呢? | 状态定义:$dp[i]$为爬到第$i$级台阶的方案数 转移方程:\(dp[i] = dp[i-1]+dp[i-2]\) 边界条件:\(dp[0]=1,dp[1]=1\) 返回值:\(dp[n]\) 空间压缩:使用长度为2的滚动数组 |
| 91. 解码方法 medium |
给定一个数字字符串,计算解码方法的总数,解码是指把数字1到26映射为字母A到Z。 | 状态定义:$dp[i]$为以第$i$个字符结尾的解码方法的总数 转移方程:\(dp[i] = \mathbb{I}(str[i] \in ['1':'9'])dp[i-1]+\mathbb{I}(str[i-1:i+1] \in ['10':'26'])dp[i-2]\) 边界条件:\(dp[0]=1 ,dp[1]=\mathbb{I}(str[0] \in ['1':'9'])\) 返回值:\(dp[n]\) 空间压缩:使用长度为2的滚动数组 |
| 198. 打家劫舍 medium |
小偷计划偷窃沿街的房屋,不能偷窃相邻的房屋,求能够偷窃到的最高金额。 | 状态定义:$dp[i]$为到达第$i$间房能偷窃到的最高金额 转移方程:\(dp[i] = \max(dp[i-1], dp[i-2]+alist[i])\) 边界条件:\(dp[0]=0,dp[1]=alist[0]\) 返回值:\(dp[n]\) 空间压缩:使用长度为2的滚动数组 |
| 213. 打家劫舍 II medium |
小偷计划偷窃沿街的房屋,不能偷窃相邻的房屋,求能够偷窃到的最高金额。第一个房屋和最后一个房屋是紧挨着的。 | 考虑到第一个房屋和最后一个房屋不能同时被选中,分别对数组$alist[0:-1]$与$alist[1:]$应用题目“198. 打家劫舍”的解法,取两个结果的最大值。 |
| 413. 等差数列划分 medium |
返回数组中所有为等差数组的子数组个数,等差数列至少有三个元素。 | 状态定义:$dp[i]$为以第$i$个元素为结尾的等差数列的数量 转移方程:\(dp[i] = \begin{cases} dp[i-1]+1, & alist[i]-alist[i-1]=alist[i-1]-alist[i-2] \\ 0, & \text{otherwise} \end{cases}\) 边界条件:\(dp[0]=0,dp[1]=0,dp[2]=0\) 返回值:\(sum(dp)\) |
| 2681. 英雄的力量 hard |
给定一个整数数组,从中选择一组下标为$i_0,i_1,…,i_k$的英雄,定义英雄的力量为$\max(nums[i_0],nums[i_1] … nums[i_k])^2 \cdot \min(nums[i_0],nums[i_1] … nums[i_k])$。返回所有可能的非空英雄组的力量之和。 | 解题思路:对数组排序,则对于以元素i结尾的任意子序列,最大值是nums[i],通过动态规划维护最小值之和 状态定义:$dp[i]$为以第$i$个元素为结尾的子序列的最小值之和 转移方程:\(dp[i] = \sum_{j=0}^{i-1}dp[j] + nums[i]\) 边界条件:\(dp[0]=0\) 返回值:\(\sum_i dp[i] \cdot nums[i]^2\) 空间压缩:引入前缀和记录$\sum_{j=0}^{i-1}dp[j]$ |
(2) 二维动态规划
| 题目 | 题干 | 解法 |
|---|---|---|
| 10. 正则表达式匹配 hard |
给定一个字符串s和一个字符规律p,实现一个支持‘.’(匹配任意单个字符)和‘*’(匹配零个或多个前面的那一个元素)的正则表达式匹配。 | 状态定义:$dp[i][j]$表示s[0:i]能否被p[0:j]匹配 转移方程:\(dp[i][j] = \begin{cases} p[j]='*' \begin{cases} dp[i][j-2], & !match(s[i],p[j]) \\ dp[i][j-2] \text{ or } dp[i-1][j], & match(s[i],p[j]) \end{cases} \\ p[j]!='*' \begin{cases} False, & !match(s[i],p[j]) \\ dp[i-1][j-1] , & match(s[i],p[j]) \end{cases} \end{cases}\) 边界条件:\(dp[0][0]=True\) 返回值:\(dp[m][n]\) |
| 62. 不同路径 medium |
找出矩阵一条从左上角到右下角的路径,每次只能向下或者向右移动一步,问总共有多少条不同的路径。 | 状态定义:$dp[i][j]$为能够到达位置$(i,j)$的路径数量 转移方程:\(dp[i][j] = dp[i-1][j] + dp[i][j-1]\) 边界条件:\(dp[i][0]=dp[0][j]=1\) 返回值:\(dp[m][n]\) 空间压缩:用$dp[j]$代表$dp[i][j]$ |
| 63. 不同路径 II medium |
找出矩阵一条从左上角到右下角的路径,每次只能向下或者向右移动一步,网格中有障碍物,问总共有多少条不同的路径。 | 状态定义:$dp[i][j]$为能够到达位置$(i,j)$的路径数量 转移方程:\(dp[i][j] = \begin{cases} dp[i-1][j] + dp[i][j-1], & grid[i][j] = 0 \\ 0, & grid[i][j] = 1\end{cases}\) 边界条件:\(dp[0][0]=\begin{cases} 1, & grid[0][0] = 0 \\ 0, & grid[0][0] = 1\end{cases}\) 返回值:\(dp[m][n]\) 空间压缩:用$dp[j]$代表$dp[i][j]$ |
| 64. 最小路径和 medium |
找出矩阵一条从左上角到右下角的路径,使得路径上的数字总和为最小,每次只能向下或者向右移动一步。 | 状态定义:$dp[i][j]$为到达位置$(i,j)$的最小路径和 转移方程:\(dp[i][j] = \begin{cases} grid[i][j]+dp[i][j-1], & i =0\\ grid[i][j]+dp[i-1][j], & j =0\\ grid[i][j]+\min(dp[i][j-1], dp[i-1][j]), & \text{otherwise} \end{cases}\) 边界条件:\(dp[0][0]=grid[0][0]\) 返回值:\(dp[m-1][n-1]\) 空间压缩:用$dp[j]$代表$dp[i][j]$ |
| 72. 编辑距离 hard |
返回将word1转换成word2所使用的最少操作数,操作包括插入、删除、替换一个字符。 | 状态定义:$dp[i][j]$为把word1[0:i]替换为word2[0:j]所使用的最少操作数 转移方程:\(dp[i][j] = \begin{cases} dp[i-1][j-1], & word1[i]=word2[j] \\ \min(dp[i][j-1],dp[i-1][j],dp[i-1][j-1])+1, & \text{otherwise} \end{cases}\) 边界条件:\(dp[i][0]=i,dp[0][j]=j\) 返回值:\(dp[m][n]\) |
| 221. 最大正方形 medium |
在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内,计算只包含 ‘1’ 的最大正方形的面积。 | 状态定义:$dp[i][j]$为以位置$(i,j)$为右下角的正方形最大边长 转移方程:\(dp[i][j] = \begin{cases} \min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1, & alist[i][j] == '1' \\ 0, & alist[i][j] == '0' \end{cases}\) 边界条件:\(dp[i][0]=1 \text{ if } alist[i][0]=\text{'1'} , dp[0][j]=1 \text{ if } alist[0][j]=\text{'1'}\) 返回值:\([\max(dp)]^2\) |
| 312. 戳气球 hard |
有 n 个气球,戳破第 i 个气球可以获得nums[i - 1] * nums[i] * nums[i + 1]枚硬币。求戳破所有的气球所能获得硬币的最大数量。 | 状态定义:$dp[i][j]$表示填满开区间$(i,j)$能得到的最多硬币数 转移方程:\(dp[i][j] = \begin{cases} \mathop{\max}_{i<k<j}(nums[i]*nums[k]*nums[j]+dp[i][k]+dp[k][j]), & i+1<j \\ 0, & i+1 \geq j \end{cases}\) 边界条件:\(dp[i][i]=0\) 返回值:\(dp[0][n+1]\) |
| 542. 01 矩阵 medium |
给定一个由 0 和 1 组成的矩阵,请输出一个大小相同的矩阵,其中每一个格子是矩阵中对应位置元素到最近的 0 的距离。 | 状态定义:$dp[i][j]$为位置$(i,j)$到最近的0的距离 转移方程:\(i=0:m;j=0:n \quad dp[i][j] = 1+\min(dp[i-1][j], dp[i][j-1]) \\ i=m:0;j=n:0 \quad dp[i][j] = 1+\min(dp[i+1][j], dp[i][j+1])\) 边界条件:\(dp[i][j]=0 \text{ if } alist[i][j]=0\) 返回值:\(dp\) 空间压缩:两次动态搜索即可完成四个方向上的查找 |
| 583. 两个字符串的删除操作 medium |
给定两个单词,每步可以删除任意一个字符串中的一个字符,返回使得两个单词相同所需的最小步数。 | 状态定义:$dp[i][j]$表示使得word1[0:i]和word2[0:j]相同所需的最小步数 转移方程:\(dp[i][j] = \begin{cases} dp[i-1][j-1], & word1[i]=word2[j] \\ \min(dp[i-1][j], dp[i][j-1])+1, & word1[i]\neq word2[j] \end{cases}\) 边界条件:\(dp[i][0]=i,dp[0][j]=j\) 返回值:\(dp[m][n]\) |
| 887. 鸡蛋掉落 hard |
给定k枚鸡蛋和n层楼的建筑。已知存在楼层f,任何从高于f的楼层落下的鸡蛋都会碎,从f楼层或比它低的楼层落下的鸡蛋都不会破。如果鸡蛋碎了就不能再次使用,如果没有摔碎则可以重复使用。计算并返回要确定f确切的值的最小操作次数。 | 状态定义:$dp[i][j]$为通过$i$次操作次数与$j$个鸡蛋能确定的最高楼层 转移方程:\(dp[i][j] = dp[i-1][j] + dp[i-1][j-1] + 1\) 边界条件:$dp=[0]_{n\times k}$ 返回值:满足$dp[i][j]\geq n$的最小$i$ |
| 931. 下降路径最小和 medium |
找出通过一个方形整数数组的下降路径的最小和。下降路径可以从第一行中的任何元素开始,并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列。 | 状态定义:$dp[i][j]$为以matrix[i][j]结尾的下降路径的最小和 转移方程:\(dp[i][j] = \min(dp[i-1][j-1],dp[i-1][j],dp[i-1][j+1])\) 边界条件:\(dp[0]=0,matrix[0]\) 返回值:\(\min(dp[-1])\) |
| 1143. 最长公共子序列 medium |
返回两个字符串的最长公共子序列(不一定连续)的长度。 | 状态定义:$dp[i][j]$为str1[0:i]和str2[0:j]的最长公共子序列长度 转移方程:\(dp[i][j] = \begin{cases} dp[i-1][j-1]+1, & str1[i]=str2[j] \\ \max(dp[i-1][j],dp[i][j-1]), & \text{otherwise} \end{cases}\) 边界条件:\(dp[i][0]=0,dp[0][j]=0\) 返回值:\(dp[m][n]\) |
| 1289. 下降路径最小和 II hard |
给定一个整数矩阵,从矩阵中的每一行选择一个数字,且按顺序选出来的数字中,相邻数字不在原数组的同一列。返回所选数字和的最小值。 | 状态定义:$dp[i][j]$为选到第$i$行第$j$列时数组和的最小值 转移方程:\(dp[i][j] = \min_{k \neq j}(dp[i-1][k]) + grid[i][j]\) 边界条件:\(dp[0][j]=grid[0][j]\) 返回值:\(\min(dp[n])\) 空间压缩:使用$m_1,m_2,m_i$分别表示上一行的最小值、次小值与最小值索引,则转移方程简化为: \(dp[i][j] =\begin{cases} m_1 + grid[i][j], & j \neq m_i \\ m_2 + grid[i][j], & j \eq m_i \end{cases}\) |
| 1388. 3n 块披萨 hard |
一个披萨由3n块不同大小的部分组成。每次挑选任意一块披萨后,Alice将会挑选逆时针方向的下一块披萨,Bob将会挑选顺时针方向的下一块披萨。重复上述过程直到没有披萨剩下。返回可以获得的披萨大小总和的最大值。 | 思路:问题等价于“从长度3n的环形序列中不相邻地选择n个数,求最大和”;分别考虑$alist[0:-1]$与$alist[1:]$。 状态定义:$dp[i][j]$为选到从前$i$个数中挑选$j$个不相邻的数的最大和 转移方程:\(dp[i][j] = \max(dp[i-2][j-1]+alist[i], dp[i-1][j])\) 边界条件:\(dp[1][1]=alist[1][1]\) 返回值:\(dp[m][n]\) |
(3) 分割问题
对于分割类型的问题,动态规划的状态转移方程通常并不依赖相邻的位置,而是依赖于满足分割条件的位置。
对于分割问题,当遍历到某个状态$i$时,往往需要考虑状态$i$之前的所有状态$j<i$,并对其中满足分割条件的状态进行计算;总时间复杂度一般为$O(N^2)$。
def seg(alist):
n = len(alist)
dp = [0]*(n+1)
dp[1] = init
for i in range(2, n+1):
for j in range(1, i):
if cond(alist[i], alist[j]):
dp[i] = f(dp[j])
| 题目 | 题干 | 解法 |
|---|---|---|
| 139. 单词拆分 medium |
给定一个字符串和一个字符串列表作为字典,判断是否可以利用字典中出现的单词拼接出字符串。 | 状态定义:$dp[i]$指示字符串前$i$个字符能否用字典拼接 分割条件:字典内的字符串 转移方程:\(dp[i] = \begin{cases} 1, & \exists \text{ word}, s[i-\text{len(word)}:i]=\text{word and }dp[i-\text{len(word)}]=1 \\ 0, & \text{otherwise} \end{cases}\) 边界条件:\(dp[0]=1\) 返回值:\(dp[n]==1\) 空间压缩:把字符串列表存储为哈希(键:字符串长度; 值:字符串集合) |
| 264. 丑数 II medium |
给定一个整数n,找出第n个丑数,丑数是只包含质因数 2、3 和/或 5 的正整数。 | 状态定义:$dp[i]$表示第$i$个丑数 分割条件:$p2,p3,p5$表示下一个丑数是当前指针指向的丑数乘以对应的质因数,更新后需要将数值等于当前丑数的指针后移1位 转移方程:\(dp[i] = \mathop{\min}_{p2,p3,p5}\left( dp[p2]*2, dp[p3]*3, dp[p5]*5\right)\) 边界条件:\(dp[1]=1\) 返回值:\(dp[n]\) |
| 279. 完全平方数 medium |
返回和为 n 的完全平方数的最少数量。 | 状态定义:$dp[i]$为和为$i$的完全平方数的最少数量 分割条件:所有不超过$i$的完全平方数 转移方程:\(dp[i] = \min_{k=1:\lfloor \sqrt{i} \rfloor}(dp[i-k^2])+1\) 边界条件:\(dp[0]=0\) 返回值:\(dp[n]\) |
| 300. 最长递增子序列 medium |
给定一个整数数组,找到其中最长严格递增子序列(不一定连续)的长度。 | 状态定义:$dp[i]$为以第$i$个数结尾的最长递增子序列长度 分割条件:两个数的大小关系 转移方程:\(dp[i] = \begin{cases} \max_{k<i} \left( dp[k] \right)+1, & alist[k]<alist[i] \\ 1, & \text{otherwise} \end{cases}\) 边界条件:\(dp[1]=1\) 返回值:\(\max(dp)\) |
| 313. 超级丑数 medium |
超级丑数是一个正整数,并满足其所有质因数都出现在质数数组$primes$中,返回第n个超级丑数。 | 状态定义:$dp[i]$表示第$i$个丑数 分割条件:$p[j]$表示下一个丑数是当前指针$j$指向的丑数乘以对应的质因数$primes[j]$,更新后需要将数值等于当前丑数的指针后移1位 转移方程:\(dp[i] = \mathop{\min}_{j}\left( dp[p[j]]*primes[j]\right)\) 边界条件:\(dp[1]=1\) 返回值:\(dp[n]\) |
| 343. 整数拆分 medium |
给定一个正整数,将其拆分为至少两个正整数的和,并使这些整数的乘积最大化。 | 状态定义:$dp[i]$表示将$i$拆分成至少两个正整数的和之后的最大乘积 分割条件:$1 \leq j <i$ 转移方程:\(dp[i] = \mathop{\max}_{j}\left( \max(j\times (i-j), j\times dp[i-j]) \right)\) 边界条件:\(dp[1]=1\) 返回值:\(dp[n]\) 空间压缩:\(j \leq 3\) |
| 646. 最长数对链 medium |
给定一个数对数组,构造数对链:当且仅当$b < c$时,数对$p2 = [c, d]$才可以跟在$p1 = [a, b]$后面。找出能够形成的最长数对链的长度。 | 状态定义:$dp[i]$为以$pairs.sort()[i]$为结尾的最长数对链的长度 分割条件:$pairs[j][1]<pairs[i][0]$ 转移方程:\(dp[i] = \mathop{\max}_{j:pairs[j][1]<pairs[i][0]}\left( dp[j]+1 \right)\) 边界条件:\(dp[i]=1\) 返回值:\(dp[n]\) |
| 650. 只有两个键的键盘 medium |
记事本上只有一个字符 ‘A’ 。每次可以对记事本进行两种操作:复制全部和粘贴,返回能够打印出 n 个 ‘A’ 的最少操作次数。 | 状态定义:$dp[i]$为能够打印出$i$个’A’的最少操作次数 分割条件:$j$是$i$的因数 转移方程:\(dp[i] = \mathop{\min}_{i\%j=0}\left( dp[j]+\frac{i}{j} \right)\) 边界条件:\(dp[1]=0\) 返回值:\(dp[n]\) |
| 823. 带因子的二叉树 medium |
给出一个含有不重复整数元素的数组,用这些整数来构建二叉树,每个整数可以使用任意次数。其中每个非叶结点的值应等于它的两个子结点的值的乘积。满足条件的二叉树一共有多少个? | 状态定义:$dp[i]$为排序后以第$i$个节点为根节点的满足条件的二叉树数量 分割条件:$l\leq r < i$ 转移方程:\(dp[i] = 1 + \sum_{l\neq r, arr[l]=arr[r]}2\cdot dp[l] \cdot dp[r]+ \sum_{l= r, arr[l]=arr[r]}dp[l] \cdot dp[r]\) 边界条件:\(dp[0]=1\) 返回值:\(sum(dp)\) |
| 1130. 叶值的最小代价生成树 medium |
给定一个正整数数组表示一个二叉树的中序遍历中每个叶节点的值。该二叉树的每个节点都有0或2个子节点,并且每个非叶节点的值等于其左子树和右子树中叶节点的最大值的乘积。在所有这样的二叉树中,返回每个非叶节点的值的最小可能总和。 | 状态定义:$dp[i][j]$表示$[i,j]$对应的子树所有非叶节点的最小总和 分割条件:$i \leq k < j$ 转移方程:\(dp[i][j] =\begin{cases} 0, & i=j \\ \min_{k\in [i,j)} \left( dp[i][k]+dp[k+1][j]+\max(arr[i:k])*\max(arr[k+1:j]) \right), & i<j \end{cases}\) 边界条件:\(dp[i][j]=\infty\) 返回值:\(dp[1][n]\) |
(4) 并行状态问题
并行状态问题是指在定义状态时同时定义多个并行的状态,在每一时刻更新每个状态时,需同时考虑上一时刻的所有状态。
| 题目 | 题干 | 解法 |
|---|---|---|
| 376. 摆动序列 medium |
返回数组中作为摆动序列的最长子序列(不一定连续)的长度。如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为摆动序列。 | 状态定义:$dp[i][0],dp[i][1]$表示以第$i$个数结尾的最长摆动子序列长度,$dp[i][0]$表示第$i$个数呈下降趋势,$dp[i][1]$表示第$i$个数呈上升趋势 分割条件:$nums[j]<nums[i], nums[k]>nums[i]$ 转移方程:\(dp[i][0] = \mathop{\max}_{k:nums[k]>nums[i]}\left( dp[k][1]+1 \right) \\ dp[i][1] = \mathop{\max}_{j:nums[j]<nums[i]}\left( dp[j][0]+1 \right)\) 边界条件:\(dp[1][0]=dp[1][1]=1\) 返回值:\(max(dp)\) 空间压缩:\(dp[i][0] = \begin{cases} dp[i-1][0], & nums[i] \geq nums[i-1] \\ \max(dp[i-1][0], dp[i-1][1]+1) , & nums[i] < nums[i-1] \end{cases} \\ dp[i][1] = \begin{cases} dp[i-1][1], & nums[i] \leq nums[i-1] \\ \max(dp[i-1][1], dp[i-1][0]+1) , & nums[i] > nums[i-1] \end{cases}\) |
| 1186. 删除一次得到子数组最大和 medium |
给定一个整数数组,返回它的某个非空子数组(连续元素)在执行一次可选的删除操作后(删除后子数组中至少应当有一个元素),所能得到的最大元素总和。 | 状态定义:$dp[i][k]$为以第$i$个元素为结尾的子数组经过$k=0,1$次删除后的最大和 转移方程:\(\begin{aligned} dp[i][0] &= \max(dp[i-1][0], 0) + alist[i] \\ dp[i][1] &= \max(dp[i-1][1] + alist[i], dp[i-1][0]) \end{aligned}\) 边界条件:\(dp[0][0]=alist[0], dp[0][1] = -\infty\) 返回值:\(\max(dp)\) 空间压缩:\(\begin{aligned} dp[1] &= \max(dp[1] + alist[i], dp[0]) \\ dp[0] &= \max(dp[0], 0) + alist[i] \end{aligned}\) |
| 1262. 可被三整除的最大和 medium |
给定一个整数数组,返回能被三整除的元素最大和。 | 状态定义:$dp[i][j]$为前$i$个元素中除以$3$余$j$的部分元素和的最大值 转移方程:\(\begin{aligned} nums[i]\%3 &= 0:\begin{cases} dp[i][0] = dp[i-1][0]+\max(0, nums[i]) \\dp[i][1] = dp[i-1][1]+\max(0, nums[i]) \\ dp[i][2] = dp[i-1][2]+\max(0, nums[i])\end{cases} \\ nums[i]\%3 &= 1:\begin{cases} dp[i][0] = \max(dp[i-1][0], dp[i-1][2]+nums[i]) \\dp[i][1] = \max(dp[i-1][1], dp[i-1][0]+nums[i]) \\ dp[i][2] = \max(dp[i-1][2], dp[i-1][1]+nums[i])\end{cases} \\ nums[i]\%3 &= 2:\begin{cases} dp[i][0] = \max(dp[i-1][0], dp[i-1][1]+nums[i]) \\dp[i][1] = \max(dp[i-1][1], dp[i-1][2]+nums[i]) \\ dp[i][2] = \max(dp[i-1][2], dp[i-1][0]+nums[i])\end{cases} \\ \end{aligned}\) 边界条件:\(dp[0][1]=dp[0][2]=-\infty\) 返回值:\(dp[n][0]\) |
| 1749. 任意子数组和的绝对值的最大值 medium |
给定一个整数数组,找出数组中和的绝对值最大的任意子数组。 | 状态定义:$dp[i][0],dp[i][1]$表示以第$i$个数为结尾的最大和与最小和 转移方程:\(dp[i][0] = \mathop{\max}\left( dp[i-1][0], 0 \right) + nums[i] \\ dp[i][1] = \mathop{\min}\left( dp[i-1][1], 0 \right)+nums[i]\) 边界条件:\(dp[0][0]=dp[0][1]=0\) 返回值:\(\max(abs(max(dp[:][0])),abs(min(dp[:][1])))\) |
| 1911. 最大子序列交替和 medium |
一个下标从0开始的数组的交替和定义为偶数下标处元素之和减去奇数下标处元素之和。给定一个数组,返回任意子序列的最大交替和。 | 状态定义:$dp[i][0],dp[i][1]$表示考虑前$i$个数的子序列最大交替和,$dp[i][0]$表示当前序列位置为偶数,$dp[i][1]$当前序列位置为奇数 转移方程:\(dp[i][0] = \mathop{\max}\left( dp[i-1][0], dp[i-1][1] + nums[i] \right) \\ dp[i][1] = \mathop{\max}\left( dp[i-1][1], dp[i-1][0]-nums[i] \right)\) 边界条件:\(dp[0][0]=dp[0][1]=0\) 返回值:\(dp[n][0]\) 空间压缩:\(dp[0] = \mathop{\max}\left( dp[0], dp[1] + nums[i] \right) \\ dp[1] = \mathop{\max}\left( dp[1], dp[0]-nums[i] \right)\) |
| 2771. 构造最长非递减子数组 medium |
给定两个整数数组,定义另一个整数数组,其每个下标处的值为两个整数数组对应元素中的任意一个。计算该整数数组中可能出现的最长非递减子数组的长度。 | 状态定义:$dp[i][0],dp[i][1]$表示以第一个或第二个数组的第$i$个元素结尾的最长非递减子数组长度 转移方程:\(dp[i][0] = \mathop{\max}\left( dp[i-1][0]I(nums1[i] \geq nums1[i-1])+1, dp[i-1][1]I(nums1[i] \geq nums2[i-1])+1\right) \\ dp[i][1] = \mathop{\max}\left( dp[i-1][0]I(nums2[i] \geq nums1[i-1])+1, dp[i-1][1]I(nums2[i] \geq nums2[i-1])+1\right)\) 边界条件:\(dp=1\) 返回值:\(max(dp)\) |
(5) 背包问题
背包问题 (knapsack problem)是一种组合优化的NP-Complete问题:有 $N$ 个物品和容量为 $W$ 的背包,每个物品都有自己的体积 $w$ 和价值 $v$,求拿哪些物品可以使得背包所装下物品的总价值最大。
如果限定每种物品只能选择 $0$ 个或 $1$ 个,则问题称为0-1背包问题;如果不限定每种物品的数量,则问题称为无界背包问题或完全背包问题。
可以用动态规划来解决背包问题。把物品的迭代放在外层,里层对体积或价值进行遍历。(空间压缩后)0-1背包对里层的体积或价值逆向遍历;完全背包对里层的体积或价值正向遍历。
⚪ 0-1背包问题
对于0-1背包,可以定义一个二维数组 $dp$ 存储最大价值,其中 $dp[i][j]$ 表示前 $i$ 件物品体积不超过 $j$ 的情况下能达到的最大价值。
在遍历到第 $i$ 件物品时,在当前背包总容量为 $j$ 的情况下,如果我们不将物品 $i$ 放入背包,那么 $dp[i][j]= dp[i-1][j]$,即前 $i$ 个物品的最大价值等于只取前 $i-1$ 个物品时的最大价值;如果我们将物品 $i$ 放入背包,假设第 $i$ 件物品体积为 $w_i$,价值为 $v_i$,那么我们得到 $dp[i][j] = dp[i-1][j-w_i] + v_i$。只需在遍历过程中对这两种情况取最大值即可,总时间复杂度和空间复杂度都为 $O(NW)$。
\[\begin{aligned} \text{状态定义:} & dp[i][j] \text{为前i件物品体积不超过j的情况下能达到的最大价值} \\ \text{转移方程:} & dp[i][j] = \begin{cases} \max(dp[i-1][j],dp[i-1][j-w_i]+v_i), & j \geq w_i \\ dp[i-1][j], & j < w_i \end{cases} \\ \text{边界条件:} & dp[0][0]=0 \\ \text{返回值:} & dp[N][W] \end{aligned}\]def knapsack(weights, values, N, W):
dp = [[0]*(W+1) for _ in range(N+1)]
for i in range(1, N+1):
w, v = weights[i-1], values[i-1]
for j in range(W+1):
if j >= w:
dp[i][j] = max(dp[i-1][j], dp[i-1][j-w]+v)
else:
dp[i][j] = dp[i-1][j]
return dp[N][W]
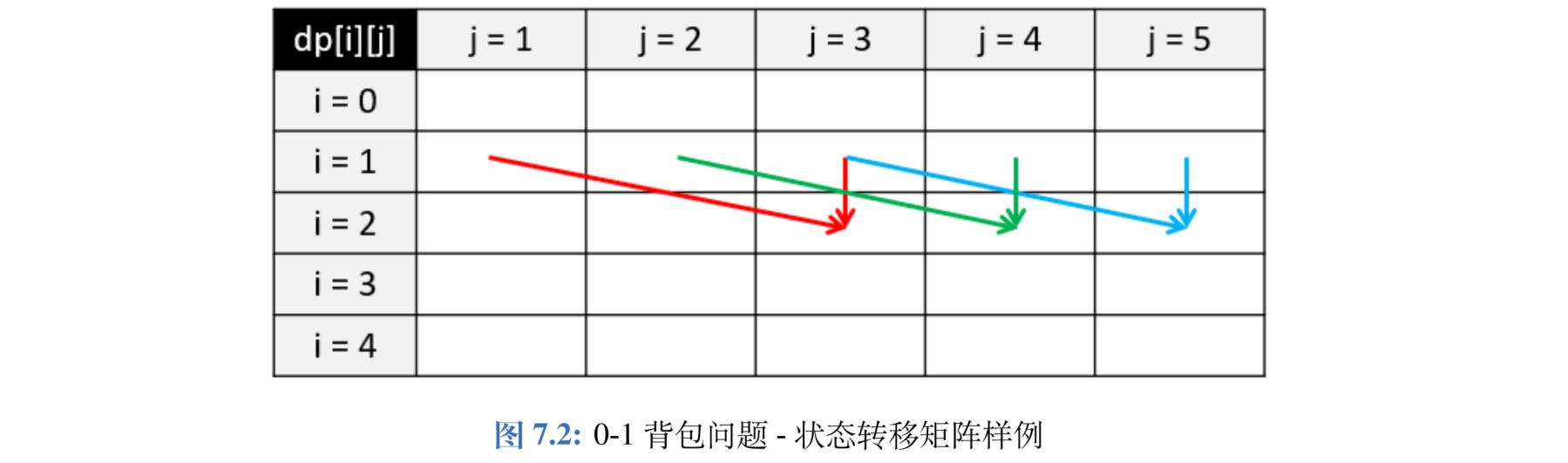
我们可以进一步对0-1背包进行空间优化,将空间复杂度降低为 $O(W)$。如图所示,假设我们目前考虑物品 $i = 2$,且其体积为 $w = 2$,价值为 $v = 3$;对于背包容量 $j$,我们可以得到 $dp[2][j]= \max(dp[1][j], dp[1][j-2] + 3)$。这里可以发现我们永远只依赖于上一排 $i = 1$ 的信息,之前算过的其他物品($i<1$)都不需要再使用。因此我们可以去掉 $dp$ 矩阵的第一个维度,在考虑物品 $i$ 时变成 $dp[j]= \max(dp[j], dp[j-w] + v)$。
这里要注意我们在遍历每一行的时候必须逆向遍历,这样才能够调用上一行物品 $i-1$ 时 $dp[j-w]$ 的值;若按照从左往右的顺序进行正向遍历,则 $dp[j-w]$ 的值在遍历到 $j$ 之前就已经被更新成物品 $i$ 的值了。
def knapsack(weights, values, N, W):
dp = [0]*(W+1)
for i in range(N):
w, v = weights[i], values[i]
for j in range(W, w-1, -1):
dp[j] = max(dp[j], dp[j-w]+v)
return dp[W]
| 题目 | 题干 | 解法 |
|---|---|---|
| 416. 分割等和子集 medium |
判断是否可以将一个只包含正整数的非空数组分割成两个元素和相等的子集。 | 状态定义:$dp[i][j]$为从数组的前$i$个元素中能否选出和为$j$的子集 转移方程:\(dp[i][j] = dp[i-1][j] \mid dp[i-1][j-alist[i]]\) 边界条件:\(dp[i][0]=True\) 返回值:\(dp[len(alist)][sum(alist)/2]\) 空间压缩:\(dp[j] = dp[j] \mid dp[j-alist[i]]\) |
| 474. 一和零 medium |
给定一个二进制字符串数组和两个整数m和n,返回数组的最大子集的长度,该子集中最多有m个0和n个1。 | 状态定义:$dp[i][j][k]$为从数组$strs[0:i]$中选出的最多有$j$个0和$k$个1的子集长度 转移方程:\(dp[i][j][k] = \max(dp[i-1][j][k],dp[i-1][j-strs[i].count('0')][k-strs[i].count('1')]+1)\) 边界条件:\(dp[0][0][0]=0\) 返回值:\(dp[len(strs)][m][n]\) 空间压缩:\(dp[j][k] = \max(dp[j][k],dp[j-strs[i].count('0')][k-strs[i].count('1')]+1)\) |
| 494. 目标和 medium |
给定一个整数数组,向数组中的每个整数前添加正或负号,求运算结果等于给定整数的不同表达式的数目。 | 解题思路:记$sum$为所有元素之和,$neg$为应取负号元素之和;则有 $(sum-neg)-neg=target$,整理得$neg=(sum-target)/2$;问题转化为求数组中所有和为$neg$的元素组合 状态定义:$dp[i][j]$为从数组$nums[0:i]$中选取元素之和等于$j$的方案数 转移方程:\(dp[i][j] = \begin{cases} dp[i-1][j]+dp[i-1][j-nums[i]], & j \geq nums[i] \\ dp[i-1][j], & j < nums[i] \end{cases}\) 边界条件:\(dp[0][0]=1\) 返回值:\(dp[n][neg]\) 空间压缩:\(dp[j] = dp[j]+dp[j-nums[i]]\) |
| 879. 盈利计划 hard |
给定工作数和成员数,以及每个工作会产生的利润和需求的成员数;计算至少产生给定利润数的工作组合数量。 | 状态定义:$dp[i][j][k]$为考虑前$i$个任务使用不超过$j$名员工能获得不小于$k$利润的计划数 转移方程:\(dp[i][j][k] = \begin{cases} dp[i-1][j][k], & j < w_i \\ dp[i-1][j][k]+dp[i-1][j-w_i][\max(0,k-v_i)], & j \geq w_i \end{cases}\) 边界条件:\(dp[i][j][0]=1\) 返回值:\(dp[tasks][n][minValue]\) 空间压缩:\(dp[j][k] = dp[j][k]+dp[j-w_i][\max(0,k-v_i)], j = n:w_i, k=minValue:0\) |
| 1049. 最后一块石头的重量 II medium |
用整数数组表示n块石头的重量。每次选出两块石头组合成重量为两者之差的绝对值的新石头,返回最后一块石头最小的可能重量。 | 解题思路:最后一块石头的重量可以表示为: \(\sum_{i=1}^n k_i \times stones_i,k_i \in \{-1,1\}\);记石头的总重量为$sum$,$ki=−1$的石头的重量之和为$neg$,则有\(\sum_{i=1}^n k_i \times stones_i = (sum-neg)-neg = sum-2\cdot neg\);要使最后一块石头的重量尽可能地小,问题转化为求在不超过$sum/2$的前提下尽可能大的$neg$。 状态定义:$dp[i][j]$表示前$i$个石头能否凑出重量$j$ 转移方程:\(dp[i][j] = \begin{cases} dp[i-1][j] \mid dp[i-1][j-stones[i]], & j \geq stones[i] \\ dp[i-1][j], & j < stones[i] \end{cases}\) 边界条件:\(dp[i][0]=True\) 返回值:\(sum-2\cdot \mathop{\max}_{dp[n][j]=True}j\) 空间压缩:\(dp[j] = dp[j] \mid dp[j-stones[i]],j=sum/2:stones[i]\) |
⚪ 完全背包问题
在完全背包问题中,一个物品可以拿多次。如图所示,假设我们遍历到物品 $i = 2$,且其体积为 $w = 2$,价值为 $v = 3$;对于背包容量 $j = 5$,最多只能装下 $2$ 个该物品。那么我们的状态转移方程就变成了 $dp[2][5] = max(dp[1][5], dp[1][3] + 3, dp[1][1] + 6)$。如果采用这种方法,假设背包容量无穷大而物体的体积无穷小,则比较次数也会趋近于无穷大,远超 $O(NW)$ 的时间复杂度。
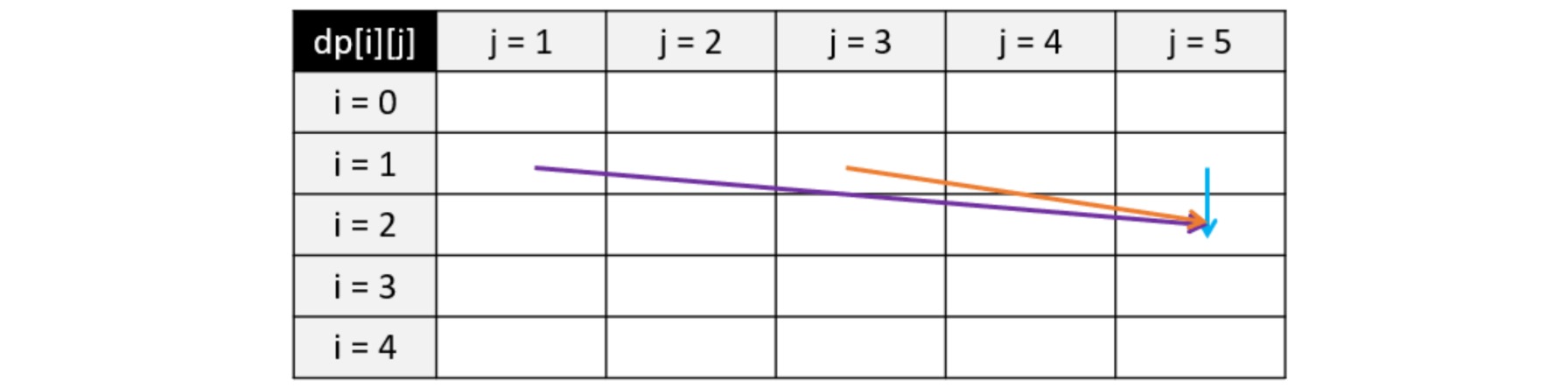
怎么解决这个问题呢?我们发现在 $dp[2][3]$ 的时候其实已经考虑了 $dp[1][3]$ 和 $dp[2][1]$ 的情况,而在 $dp[2][1]$ 时也已经考虑了 $dp[1][1]$ 的情况。因此,如图所示,对于拿多个物品的情况,我们只需考虑 $dp[2][3]$ 即可,即 $dp[2][5] = max(dp[1][5], dp[2][3] + 3)$。

这样,我们就得到了完全背包问题的状态转移方程:$dp[i][j] = \max(dp[i-1][j], dp[i][j-w_i] + v_i)$,其与 0-1 背包问题的差别仅仅是把状态转移方程中的第二个 $i-1$ 变成了 $i$。
\[\begin{aligned} \text{状态定义:} & dp[i][j] \text{为前i件物品体积不超过j的情况下能达到的最大价值} \\ \text{转移方程:} & dp[i][j] = \begin{cases} \max(dp[i-1][j],dp[i][j-w_i]+v_i), & j \geq w_i \\ dp[i-1][j], & j < w_i \end{cases} \\ \text{边界条件:} & dp[0][0]=0 \\ \text{返回值:} & dp[N][W] \end{aligned}\]def knapsack(weights, values, N, W):
dp = [[0]*(W+1) for _ in range(N+1)]
for i in range(1, N+1):
w, v = weights[i-1], values[i-1]
for j in range(W+1):
if j >= w:
dp[i][j] = max(dp[i-1][j], dp[i][j-w]+v)
else:
dp[i][j] = dp[i-1][j]
return dp[N][W]
同样的,我们也可以利用空间压缩将空间复杂度降低为 $O(W)$,去掉 $dp$ 矩阵的第一个维度,在考虑物品 $i$ 时变成 $dp[j]= \max(dp[j], dp[j-w] + v)$。这里要注意在遍历每一行的时候必须正向遍历,因为我们需要利用当前物品 $i$ 在第 $j-w$ 列的信息。
def knapsack(weights, values, N, W):
dp = [0]*(W+1)
for i in range(N):
w, v = weights[i], values[i]
for j in range(w, W+1):
dp[j] = max(dp[j], dp[j-w]+v)
return dp[W]
| 题目 | 题干 | 解法 |
|---|---|---|
| 39. 组合总和 medium |
给定一个无重复元素的整数数组和一个目标整数,找出数组中可以使数字和为目标数的所有不同组合,数组中的同一个数字可以无限制重复被选取。 | 状态定义:$dp[i][j]$为重复使用前$i$个数字凑成和为$j$的不同组合列表 转移方程:\(dp[i][j] = dp[i-1][j].extend(dp[i][j-nums[i]].append(nums[i]))\) 边界条件:\(dp[0][0]=[]\) 返回值:\(dp[n][target]\) 空间压缩:\(dp[j] = dp[j].extend(dp[j-nums[i]].append(nums[i]))\) |
| 322. 零钱兑换 medium |
给定一个整数数组表示不同面额的硬币,每种硬币的数量是无限的;以及一个整数表示总金额。计算可以凑成总金额所需的最少的硬币个数。 | 状态定义:$dp[i][j]$为重复使用前$i$个硬币凑成总金额$j$的最少硬币个数 转移方程:\(dp[i][j] = \min(dp[i-1][j],dp[i][j-coins[i]]+1)\) 边界条件:\(dp[0][0]=0,dp[0][1:]=amount+2\) 返回值:\(\begin{cases} dp[m][n], & dp[m][n]<amount+2 \\ -1, & \text{otherwise} \end{cases}\) 空间压缩:\(dp[j] = \min(dp[j],dp[j-coins[i]]+1)\) |
| 518. 零钱兑换 II medium |
给定一个整数数组表示不同面额的硬币,每种硬币的数量是无限的;以及一个整数表示总金额。计算可以凑成总金额的硬币组合数。 | 状态定义:$dp[i][j]$为重复使用前$i$个硬币凑成总金额$j$的组合数 转移方程:\(dp[i][j] = \begin{cases} dp[i-1][j]+dp[i][j-coins[i]], & j\geq coins[i] \\ dp[i-1][j], & j<coins[i] \end{cases}\) 边界条件:\(dp[i][0]=1\) 返回值:\(dp[m][n]\) 空间压缩:\(dp[j] = dp[j]+dp[j-coins[i]],j=coins[i]:n\) |
| 1449. 数位成本和为目标值的最大数字 medium |
给定使用数位’1’-‘9’的成本和一个目标数,返回总成本恰好为目标对应的最大整数。 | 状态定义:$dp[i][j]$为重复使用前$i$个数位凑成总成本$j$的最大数字 转移方程:\(dp[i][j] = \begin{cases} str\_max(dp[i-1][j], dp[i][j-coins[i]].max\_insert(i)), & j\geq cost[i] \\ dp[i-1][j], & j<cost[i] \end{cases}\) 边界条件:\(dp[i][0]='0'\) 返回值:\(dp[m][n]\) 空间压缩:\(dp[j] = str\_max(dp[j], dp[j-coins[i]].max\_insert(i))\) |
(6) 股票问题
股票交易类问题通常可以用动态规划来解决。对于稍微复杂一些的股票交易类问题,比如需要冷却时间或者交易费用,则可以用通过动态规划实现的状态机来解决。
状态机的思想在于列举出所有可能的「状态」,然后穷举更新这些「状态」。具体到每一天,看看总共有几种可能的「状态」,再找出每个「状态」对应的「选择」。我们要穷举所有「状态」,穷举的目的是根据对应的「选择」更新状态。
for 状态1 in 状态1的所有取值:
for 状态2 in 状态2的所有取值:
for ...
dp[状态1][状态2][...] = 择优(选择1,选择2...)
股票类型的通用题目形式为给定一支股票每天的价格$prices$,并限制最大交易次数为$K$,计算能够获得的最大利润。这个问题的「状态」有三个,第一个是天数,第二个是当前的交易次数,第三个是当前的持有状态(rest,用 1 表示持有,0 表示没有持有)。每天都有三种「选择」:买入(buy)、卖出(sell)、无操作(rest)。可以用三维数组存储该问题的三种状态:
dp[i][k][0 or 1]
0 <= i <= n, 0 <= k <= K
for 1 <= i <= n:
for 1 <= k <= K:
for s in {0, 1}:
dp[i][k][s] = max(buy, sell, rest)
股票问题的最终答案是$dp[n][K][0]$,即最后一天,最多进行 $K$ 次交易,最多获得多少利润。注意答案不应是$dp[n][K][1]$,因为最后手上还持有股票得到的利润一定小于手上的股票卖出得到的利润。
根据「状态」的定义可以画出状态转移图,对应一个有限状态机:
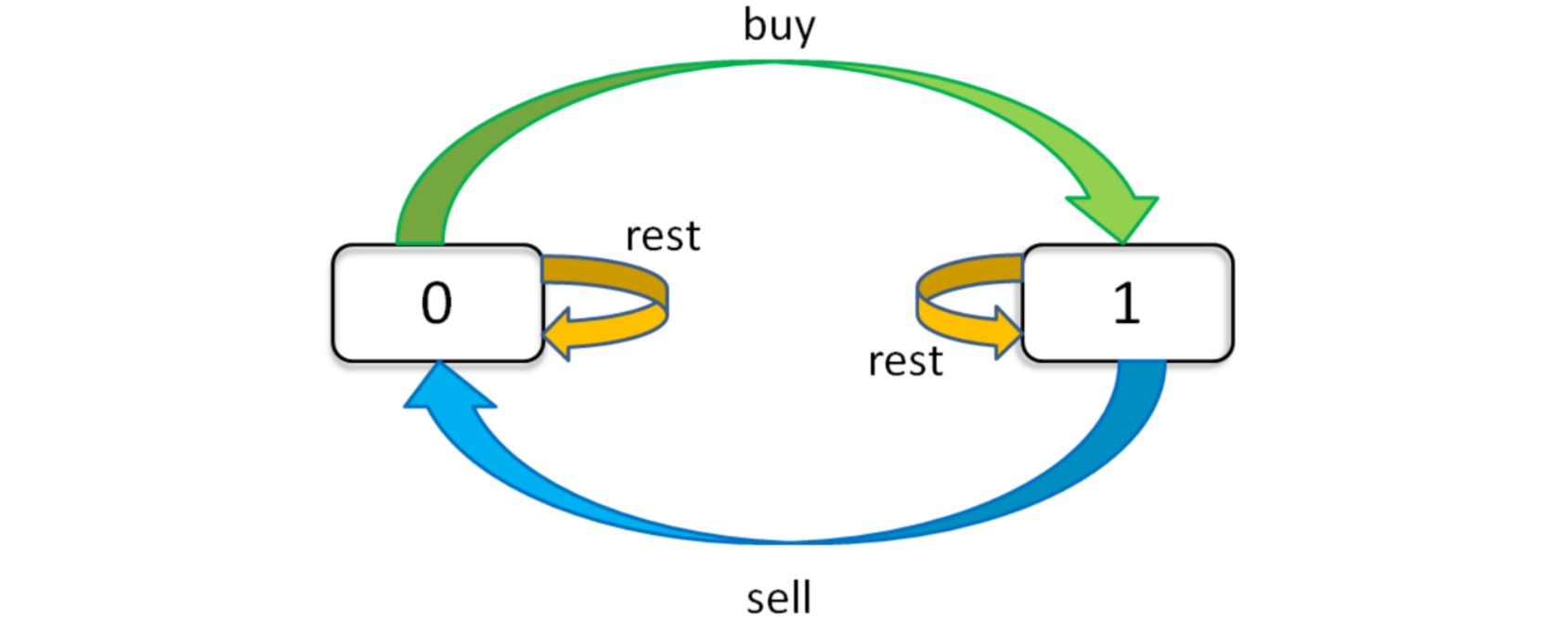
并进一步写出状态转移方程:
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i-1])
解释:今天我没有持有股票,有两种可能:
要么是我昨天就没有持有,然后今天选择 rest,所以我今天还是没有持有;
要么是我昨天持有股票,但是今天我 sell 了,所以我今天没有持有股票了。
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i-1])
解释:今天我持有着股票,有两种可能:
要么我昨天就持有着股票,然后今天选择 rest,所以我今天还持有着股票;
要么我昨天本没有持有,但今天我选择 buy,所以今天我就持有股票了。
还需要定义状态机的初始条件:
dp[0][k][0] = 0
解释:因为 i 是从 1 开始的,所以 i = 0 意味着还没有开始,这时候的利润当然是 0 。
dp[0][k][1] = -infinity
解释:还没开始的时候,是不可能持有股票的,用负无穷表示这种不可能。
dp[i][0][0] = 0
解释:因为 k 是从 1 开始的,所以 k = 0 意味着根本不允许交易,这时候利润当然是 0 。
dp[i][0][1] = -infinity
解释:不允许交易的情况下,是不可能持有股票的,用负无穷表示这种不可能。
| 题目 | 题干 | 状态机 |
|---|---|---|
| 121. 买卖股票的最佳时机 easy |
给定一支股票每天的价格,只能买卖一次,计算所能获取的最大利润。 | 初始状态:\(dp[0][0] = 0, \quad dp[0][1] = -1e9\) 转移方程:\(\begin{aligned} dp[i][0] &= \max(dp[i-1][0], dp[i-1][1]+prices[i-1]) \\ dp[i][1] &= \max(dp[i-1][1], -prices[i-1]) \end{aligned}\) 空间压缩:\(\begin{aligned} dp[0] &= \max(dp[0], dp[1]+prices[i-1]) \\ dp[1] &= \max(dp[1], -prices[i-1]) \end{aligned}\) |
| 122. 买卖股票的最佳时机 II medium |
给定一支股票每天的价格,不限制购买次数,计算所能获取的最大利润。 | 初始状态:\(dp[0][0] = 0, \quad dp[0][1] = -1e9\) 转移方程:\(\begin{aligned} dp[i][0] &= \max(dp[i-1][0], dp[i-1][1]+prices[i-1]) \\ dp[i][1] &= \max(dp[i-1][1], dp[i-1][0]-prices[i-1]) \end{aligned}\) 空间压缩:\(\begin{aligned} s0 &= \max(dp[0], dp[1]+prices[i-1]) \\ s1 &= \max(dp[1], dp[0]-prices[i-1]) \\ dp &= [s0, s1] \end{aligned}\) |
| 123. 买卖股票的最佳时机 III hard |
给定一支股票每天的价格,最多可以完成两笔交易,计算所能获取的最大利润。 | 初始状态:\(\begin{aligned} dp[0][k][0] &= dp[i][0][0] = 0 \\ dp[0][k][1] &= dp[i][0][1] = -1e9 \end{aligned}\) 转移方程:\(\begin{aligned} dp[i][k][0] &= \max(dp[i-1][k][0], dp[i-1][k][1]+prices[i-1]) \\ dp[i][k][1] &= \max(dp[i-1][k][1], dp[i-1][k-1][0]-prices[i-1]) \end{aligned}\) 空间压缩:\(\begin{aligned} dp[k][0] &= \max(dp[k][0], dp[k][1]+prices[i-1]) \\ dp[k][1] &= \max(dp[k][1], dp[k-1][0]-prices[i-1]) \end{aligned}\) $\quad$ (由于计算$dp[k]$用到之前的$dp[k-1]$,因此要倒序遍历$k=2,1$) |
| 188. 买卖股票的最佳时机 IV hard |
给定一支股票每天的价格,最多可以完成k笔交易,计算所能获取的最大利润。 | 初始状态:\(\begin{aligned} dp[0][k][0] &= dp[i][0][0] = 0 \\ dp[0][k][1] &= dp[i][0][1] = -1e9 \end{aligned}\) 转移方程:\(\begin{aligned} dp[i][k][0] &= \max(dp[i-1][k][0], dp[i-1][k][1]+prices[i-1]) \\ dp[i][k][1] &= \max(dp[i-1][k][1], dp[i-1][k-1][0]-prices[i-1]) \end{aligned}\) 空间压缩:\(\begin{aligned} dp[k][0] &= \max(dp[k][0], dp[k][1]+prices[i-1]) \\ dp[k][1] &= \max(dp[k][1], dp[k-1][0]-prices[i-1]) \end{aligned}\) $\quad$ (由于计算$dp[k]$用到之前的$dp[k-1]$,因此要倒序遍历$k$) |
| 309. 最佳买卖股票时机含冷冻期 medium |
给定一支股票每天的价格,不限制购买次数,计算所能获取的最大利润。卖出股票后无法在第二天买入股票 (即冷冻期为 1 天)。 | 状态定义:$0$表示未持股,无冷冻;$1$表示未持股,冷冻;$2$表示持股 初始状态:\(dp[0][0] = 0, \quad dp[0][1] = -1e9, \quad dp[0][2] = -1e9\) 转移方程:\(\begin{aligned} dp[i][0] &= \max(dp[i-1][0], dp[i-1][1]) \\ dp[i][1] &= dp[i-1][2]+prices[i-1] \\ dp[i][2] &= \max(dp[i-1][2], dp[i-1][0]-prices[i-1]) \end{aligned}\) 空间压缩:\(\begin{aligned} dp[i][0] &= \max(dp[i-1][0], dp[i-1][1]+prices[i-1]) \\ dp[i][1] &= \max(dp[i-1][1], dp[i-2][0]-prices[i-1]) \end{aligned}\) |
| 714. 买卖股票的最佳时机含手续费 medium |
给定一支股票每天的价格,不限制购买次数,计算所能获取的最大利润。每笔交易都需要付手续费。 | 初始状态:\(dp[0][0] = 0, \quad dp[0][1] = -1e9\) 转移方程:\(\begin{aligned} dp[i][0] &= \max(dp[i-1][0], dp[i-1][1]+prices[i-1])-fee \\ dp[i][1] &= \max(dp[i-1][1], dp[i-1][0]-prices[i-1]) \end{aligned}\) 空间压缩:\(\begin{aligned} s0 &= \max(dp[0], dp[1]+prices[i-1]-fee) \\ s1 &= \max(dp[1], dp[0]-prices[i-1]) \\ dp &= [s0, s1] \end{aligned}\) |
(6) 树形动态规划问题
树形动态规划是指在树上进行的动态规划。因为树固有的递归属性,所以树形动态规划一般都是递归进行的。
判断一个问题是否为树形动态规划问题,首先判断是否是一个树,然后是否符合动态规划要求,也就是去判断父节点和子节点是否存在阶段性的关联关系。通常树形DP的写法有两种:
- 根到叶子: 首先在根节点上进行计算,再将结果传递给子节点。这种动态规划在实际的问题中运用的不多。
- 叶子到根: 根的子节点传递有用的信息给根,然后从根得出最优解的过程。这类的习题比较多。
树形DP的伪代码如下:
def dfs(root):
# 递归处理root的每一个节点son
dfs(root.son)
# 根据转移方程动态更新
| 题目 | 题干 | 解法 |
|---|---|---|
| 337. 打家劫舍 III medium |
这个地方的所有房屋的排列类似于一棵二叉树。如果两个直接相连的房子在同一天晚上被打劫,房屋将自动报警。返回在不触动警报的情况下,小偷能够盗取的最高金额。 | 状态定义:$dp[node][0]$表示不打劫$node$节点能够盗取的最高金额 $\qquad dp[node][1]$表示打劫$node$节点能够盗取的最高金额 转移方程:\(\begin{cases}dp[node][0] &= \max(dp[node.left][0], dp[node.left][1])+\max(dp[node.right][0], dp[node.right][1]) \\ dp[node][1] &= node.val + dp[node.left][0] + dp[node.right][0] \end{cases}\) 边界条件:\(dp[leaf]=[0, 0]\) 返回值:\(\max(dp[root][0], dp[root][1])\) |
(6) 子集枚举问题
如果一个问题中状态的本征维度比较低(比如$n=15$,最多存在$2^{15}=32768$个状态),则可以考虑在构造状态转移方程时枚举所有状态。
在遍历状态时可以通过二进制的子集枚举实现。对于一个有 $k$ 个 $1$ 的二进制表示的正整数 $x$,其非空子集(至少包含一个$1$)有 $2^k - 1$ 个。此时枚举子集的时间复杂度为 $O(2^k)$。子集枚举可以通过位运算实现:
for s in range(1 << k):
# s表示当前时刻可以取到的所有状态的集合,取值为 [0, 2^k-1]
# 例①:枚举s的所有非空子集:
sub = s
while sub:
# 处理状态sub
sub = (sub - 1) & s
# 例②:
⚪ 分治法
分治问题由“分”(divide)和“治”(conquer)两部分组成,通过把原问题分为子问题,再将子问题进行处理合并,从而实现对原问题的求解。
可以使用数学表达式来表示分治过程。定义 $T(n)$ 表示处理一个长度为 $n$ 的数组的时间复杂度,则分治法的时间复杂度递推公式为 $T(n) = 2T(n/2) + O(n)$。其中 $2T(n/2)$ 表示我们分成了两个长度减半的子问题,$O(n)$ 则为合并两个长度为 $n/2$ 数组的时间复杂度。
可以利用主定理(Master theorem)求解最终的时间复杂度:考虑$T(n) = aT(n/b) + f(n)$,定义 $k=\log_b a$:
- 如果 $f(n)=O(n^p)$ 且 $p<k$,那么 $T(n)=O(n^k)$;
- 如果存在 $c\geq 0$ 满足 $f(n)=O(n^k \log^c n)$,那么 $T(n)=O(n^k \log^{c+1} n)$;
- 如果 $f(n)=O(n^p)$ 且 $p>k$,那么 $T(n)=O(f(n))$。
分治问题可以通过主定理求得时间复杂度。如上文定义的递推公式$T(n) = 2T(n/2) + O(n)$的时间复杂度为$O(n \log n)$。
以归并排序算法为例,分治法的一般写法如下:
def divide(alist):
if len(alist) <= 1:
return alist
num = len(alist)//2
left = divide(alist[0:num])
right = divide(alist[num:])
return conquer(left, right)
def conquer(left, right):
result = []
l, r = 0, 0
while l<len(left) and r<len(right):
if left[l] <= right[r]:
result.append(left[l])
l += 1
else:
result.append(right[r])
r += 1
result += left[l:] # 切片超界会返回空列表
result += right[r:]
return result
| 题目 | 题干 | 解法 |
|---|---|---|
| 23. 合并 K 个升序链表 hard |
给定一个链表数组,每个链表都已经按升序排列,将所有链表合并到一个升序链表中。 | \(\begin{aligned} \text{分:} & \text{将k个链表分成两组} \\ \text{治:} & \text{合并两个链表} \end{aligned}\) |
| 241. 为运算表达式设计优先级 medium |
给一个由数字和运算符(+,-,*)组成的字符串,按不同优先级组合数字和运算符,计算并返回所有可能组合的结果。 | \(\begin{aligned} \text{分:} & \text{按字符+,-,*拆分字符串} \\ \text{治:} & \text{按字符+,-,*合并结果} \end{aligned}\) |
| 932. 漂亮数组 medium |
构造由范围 [1, n] 的整数组成的一个排列,对于每个 0 <= i < j < n ,均不存在下标 k(i < k < j)使得 2 · nums[k] == nums[i] + nums[j]。 | \(\begin{aligned} \text{思路:} & 2 * nums[k] != nums[i] + nums[j] \text{ 左端为偶数} \\ & \text{不妨取右端为奇数:i<k为奇数,j>k为偶数} \\ & \text{注意到线性变换a*nums+b不改变不等式关系} \\ \text{分:} & \text{构造从1到(N + 1)/2的所有整数的漂亮数组} \\ & \text{构造从1到N/2的所有整数的漂亮数组} \\ \text{治:} & \text{把从1到(N + 1)/2的漂亮数组映射成$1$到$N$范围的所有奇数} \\ & \text{把从1到N/2的漂亮数组映射成$1$到$N$范围的所有偶数} \end{aligned}\) |
⚪ 位运算
位运算是算法题里比较特殊的一种类型,它们利用二进制位运算的特性进行一些奇妙的优化和计算。
Python实现整型与二进制之间的转换:
# 整型 -> 二进制
b = bin(n) # 返回一个整数n的以'0b'开始的二进制表示形式的字符串。
b = '{0:b}'.format(n) # 返回一个整数n的二进制表示形式的字符串。
# 二进制 -> 整型
n = int(b, 2) # 把二进制字符串转换为整型
常用的位运算符号包括:
"""
& 按位与 | 按位或 ^ 按位异或 ~ 按位取反
<< 按位左移:相当于乘以2,运算优先级较低
>> 按位右移:相当于整除2,运算优先级较低
"""
以下是一些常见的位运算特性,其中 0s 和 1s 分别表示只由 0 或 1 构成的二进制数字。
x ^ 0s = x x & 0s = 0 x | 0s = x
x ^ 1s = ~x x & 1s = x x | 1s = 1s
x ^ x = 0 x & x = x x | x = x
下面是一些位运算的技巧:
n & 1:可以取出 n 的最后一位。n & (n+1):可以判断 n 的二进制表示是否全为 1。n & (n-1):可以去除 n 的位级表示中为1的最低的那一位,例如对于二进制表示 11110100,减去 1 得到 11110011,这两个数按位与得到 11110000。n & (-n):可以得到 n 的位级表示中1的最低的那一位,例如对于二进制表示 11110100,取负得到 00001100(负数以补码的形式表示,最高位即符号位,剩下的位按位取反,末位加1),这两个数按位与得到 00000100。n.bit_count():统计n在二进制表示中位为$1$的数量
| 题目 | 题干 | 解法 |
|---|---|---|
| 136. 只出现一次的数字 easy |
给定一个整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。 | 将数组内所有的数字进行按位异或。出现两次的所有数字按位异或的结果是 0,0 与出现一次的数字异或可以得到这个数字本身。 n^n=0, n^0=n |
| 137. 只出现一次的数字 II medium |
给定一个整数数组,除某个元素仅出现一次外,其余每个元素都恰出现三次。找出那个只出现了一次的元素。 | 答案的第i个二进制位就是数组中所有元素的第i个二进制位之和除以3的余数。注意第31个二进制位(即最高位)是补码意义下的符号位,若为1则应进行操作ans-=(1<<31)。 |
| 190. 颠倒二进制位 easy |
颠倒给定的 32 位无符号整数的二进制位。 | 使用算术左移和右移,可以很轻易地实现二进制的翻转。 ans<<=1, ans+=n&1, n>>=1 |
| 231. 2 的幂 easy |
给定一个整数 n,判断该整数是否是 2 的幂次方。 | 如果一个数字n是2的整数次方,那么它的二进制一定是10…0的形式;考虑到n−1的二进制是01…1,这两个数求按位与的结果一定是0。 n>0 and n&(n-1)==0 |
| 260. 只出现一次的数字 III medium |
给定一个整数数组 ,其中恰好有两个元素只出现一次,其余所有元素均出现两次。找出只出现一次的那两个元素。 | 将数组内所有的数字进行按位异或得到这两个数按位异或的结果,使用位运算x&(-x)取出其二进制表示中最低位那个 1,并按照这一位是否为1把所有元素分成两类,对于任意一个在数组中只出现了一次的元素,即它们会被包含在不同类中。 |
| 268. 丢失的数字 easy |
给定一个包含 [0, n] 中 n 个数的数组,找出 [0, n] 这个范围内没有出现在数组中的那个数。 | 在数组后面添加从 0 到 n 的每个整数,把问题转换成“136. 只出现一次的数字”。 |
| 318. 最大单词长度乘积 medium |
给定一个字符串数组 ,找出数组中两个单词长度乘积的最大值,并且这两个单词不含有公共字母。 | 遍历字符串数组中的每一对单词,通过位运算操作判断两个单词是否有公共字母。 |
| 326. 3 的幂 easy |
给定一个整数,判断它是否是 3 的幂次方。 | 一个数乘以3相当于一个数左移(乘以2)再加这个数。n*3 == (n<<1) + n |
| 338. 比特位计数 easy |
给定一个整数 n,计算其二进制表示中 1 的个数。 | \(\begin{aligned} \text{状态定义:} & dp[i] \text{表示数字 i 的二进制含有 1 的个数} \\ \text{转移方程:} & dp[i] = \begin{cases} dp[i-1]+1,& \text{i 的最后一位为1} \\ dp[i>>1],& \text{i 的最后一位为0} \end{cases} \\ \text{边界条件:} & dp[0]=0 \\ \text{返回值:} & dp \end{aligned}\) |
| 342. 4的幂 easy |
给定一个整数 n,判断该整数是否是 4 的幂次方。 | 如果一个数字n是4的整数次方,那么它一定是2的整数次方,并且二进制表示中 1 的位置必须为奇数位;把 n 和二进制的 10101…101(即十进制下的 1431655765)做按位与。 n>0 and n&(-n)==n and n&int('10'*15+'1',2)!=0 |
| 461. 汉明距离 easy |
计算两个整数之间的汉明距离,两个整数之间的汉明距离指的是这两个数字对应二进制位不同的位置的数目。 | 对两个数进行按位异或操作,统计有多少个 1 即可。 bin(x^y).count('1') |
| 476. 数字的补数 easy |
给定一个整数,输出它的补数。对整数的二进制表示取反后,再转换为十进制表示,可以得到这个整数的补数。 | 构造全1掩码并与原数进行异或运算。 int('1'*(len(bin(num))-2), 2)^num |
| 693. 交替位二进制数 easy |
给定一个正整数,检查它的二进制表示是否总是 0、1 交替出现。 | 当且仅当输入 n 为交替位二进制数时,n^(n>>1) 的二进制表示全为 1,当且仅当 a 的二进制表示全为 1 时,a&(a+1)结果为 0。 |
| 1356. 根据数字二进制下 1 的数目排序 easy |
给定一个整数数组,将数组中的元素按照其二进制表示中数字1的数目升序排序。 | 使用bin_count()方法统计1的数目,然后对其索引进行排序。 |
⚪ 数学问题
(1)模拟求和
模拟求和问题通常会涉及到进位以及位数差的处理。
| 题目 | 题干 | 解法 |
|---|---|---|
| 2. 两数相加 medium |
给定两个按照逆序的方式存储数字的链表,表示两个非负的整数。返回一个表示两数之和的链表。 | 模拟求和过程,注意进位和位数差。 |
| 66. 加一 easy |
给定一个由整数组成的非空数组所表示的非负整数,在该数的基础上加一。 | 模拟加一运算,从后往前考虑进位细节。 |
| 67. 二进制求和 easy |
给定两个二进制字符串,以二进制字符串的形式返回它们的和。 | 从后往前逐位模拟二进制加法运算,考虑进位、位数差等细节。 |
| 415. 字符串相加 easy |
给定两个字符串形式的非负整数,计算它们的和并同样以字符串形式返回。 | 从后往前逐位模拟加法运算,考虑进位、位数差等细节。 |
| 445. 两数相加 II medium |
给定两个非空链表来代表两个非负整数。数字最高位位于链表开始位置。它们的每个节点只存储一位数字。将这两数相加会返回一个新的链表。 | 使用栈存储两个链表的数值,然后模拟求和过程,注意进位和位数差。 |
(2)数论
利用辗转相除法,我们可以很方便地求得两个数的最大公因数(greatest common divisor,gcd);将两个数相乘再除以最大公因数即可得到最小公倍数(least common multiple, lcm)。
def gcd(a, b):
return a if b == 0 else gcd(b, a%b)
def lcm(a, b):
return a * b / gcd(a, b)
| 题目 | 题干 | 解法 |
|---|---|---|
| 168. Excel表列名称 easy |
给定一个整数,返回它在 Excel 表中相对应的列名称(A->1,Z->26,AA->27)。 | 等价于26进制转换问题。注意取值从1开始,因此执行divmod()前应减去1(对齐到$[0,25]$)。 |
| 169. 多数元素 easy |
给定一个数组,返回其中的多数元素。多数元素是指在数组中出现次数大于数组长度的一半的元素。 | Boyer-Moore投票算法:第一个到来的士兵,直接插上自己阵营的旗帜占领这块高地;如果新来的士兵和前一个士兵是同一阵营,则集合起来占领高地;如果新来到的士兵不是同一阵营,则前方阵营派一个士兵和它同归于尽;当下一个士兵到来,发现前方阵营已经没有兵力,新士兵就成了领主。 |
| 172. 阶乘后的零 medium |
给定一个整数n,返回n的阶乘结果中尾随零的数量。 | n的阶乘尾零的数量即为其中因子10的个数,由于质因子 5 的个数不会大于质因子 2 的个数,因此统计 [1,n] 的每个数的质因子 5 的个数之和。 |
| 204. 计数质数 medium |
给定整数n,返回所有小于非负整数n的质数的数量。质数指的是指在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数。 | 埃拉托斯特尼筛法(Sieve of Eratosthenes,简称埃氏筛法):从 1 到 n 遍历,假设当前遍历到 m,则把所有小于 n 的、且是 m 的倍数的整数标为合数;遍历完成后,没有被标为合数的数字即为质数。 |
| 504. 七进制数 easy |
给定一个整数,将其转化为 7 进制,并以字符串形式输出。 | 进制转换类型的题目,通常是利用除法和取模运算divmod()来进行计算。 |
| 462. 最小操作次数使数组元素相等 II medium |
给定一个整数数组,返回使所有数组元素相等需要的最小操作数。在一次操作中,可以使数组中的一个元素加 1 或者减 1。 | 使所有数组元素相等的取值应为数组的中位数。 |
(3)几何
| 题目 | 题干 | 解法 |
|---|---|---|
| 149. 直线上最多的点数 hard |
给定一个数组,其中每个元素表示 X-Y 平面上的一个点。求最多有多少个点在同一条直线上。 | 对于每个点,对其它点建立字典,统计同一斜率的点一共有多少个,要考虑斜率不存在和重复坐标的情况。 |
| 223. 矩形面积 medium |
给定二维平面上两个由直线构成且边与坐标轴平行/垂直的矩形,计算并返回两个矩形覆盖的总面积。 | 总面积(并集)= 两个矩形面积之和 - 重叠区域面积(交集)。 |
| 836. 矩形重叠 easy |
与坐标轴平行的矩形以列表$[x_1, y_1, x_2, y_2]$的形式表示,其中$(x_1, y_1)$为左下角的坐标,$(x_2, y_2)$是右上角的坐标。给定两个矩形,判断它们是否重叠。如果相交的面积为正,则称两矩形重叠。 | 先求重叠部分的左下角坐标$(x_{bl},y_{bl})$与右上角坐标$(x_{tr},y_{tr})$: \(x_{bl} = \max(x_1^a,x_1^b), y_{bl} = \max(y_1^a,y_1^b) \\ x_{tr} = \min(x_2^a,x_2^b), y_{tr} = \min(y_2^a,y_2^b)\) 然后判断重叠部分是否为正。 |
| 1401. 圆和矩形是否有重叠 medium |
给定一个圆$(r, x_{Center}, y_{Center})$和一个与坐标轴平行的矩形的左下角与右上角坐标$(x_1, y_1, x_2, y_2)$,判断圆和矩形是否有重叠的部分(包括点落在边界上的情况)。 | 先求矩形中与圆心距离最近的点$(x_{\min},y_{\min})$: \(x_{\min} = \begin{cases} x_1, & x_{Center} < x_1 \\ x_2, & x_{Center} > x_2 \\ x_{Center}, & \text{otherwise} \end{cases} \\ y_{\min} = \begin{cases} y_1, & y_{Center} < y_1 \\ y_2, & y_{Center} > y_2 \\ y_{Center}, & \text{otherwise} \end{cases}\) 然后判断点$(x_{\min},y_{\min})$与圆心的距离是否超过半径。 |
(4)随机采样
# 从$[0, 1)$中随机采样一个浮点数数
p = random.random()
# 从$[1, n)$中随机采样一个整数
i = random.randrange(1, n, step=1)
# 随机打乱一个数组:
random.shuffle(alist)
| 题目 | 题干 | 解法 |
|---|---|---|
| 382. 链表随机节点 medium |
给定一个单链表,随机选择链表的一个节点,并返回相应的节点值。每个节点被选中的概率一样。 | 水库采样算法:在遍历到第 $m$ 个节点时,有 $1/m$ 的概率选择这个节点覆盖掉之前的节点选择。对于长度为 $n$ 的链表的第 $m$ 个节点,最后被采样的充要条件是它被选择,且之后的节点都没有被选择。这种情况发生的概率为 $\frac{1}{m}\times\frac{m}{m+1}\times\frac{m+1}{m+2}\times \cdots \times \frac{n-1}{n}=\frac{1}{n}$。因此每个点都有均等的概率被选择。 |
| 384. 打乱数组 medium |
给定一个整数数组,设计算法来打乱一个没有重复元素的数组。 | Fisher-Yates洗牌算法:通过随机交换位置来实现随机打乱。按$0\leq i <n$遍历数组,对于每次循环,在 $[i,n)$ 中随机抽取一个下标 $j$,将第 $i$ 个元素与第 $j$ 个元素交换。 |
| 398. 随机数索引 medium |
给定一个可能含有重复元素的整数数组,随机输出给定的目标数字的索引。如果存在多个有效的索引,则每个索引的返回概率应当相等。 | 使用哈希字典存储每个数字的所有索引,然后随机采样一个索引。 |
| 470. 用 Rand7() 实现 Rand10() medium |
给定方法 rand7 可生成 [1,7] 范围内的均匀随机整数,试写一个方法 rand10 生成 [1,10] 范围内的均匀随机整数。 | 古典概型:构造 2 次采样,分别有 2 种(如rand7 拒绝 7,相当于对 [1,6] 采样,把奇数和偶数作为 2 种结果)和 5 种结果(如rand7 拒绝 6,7,然后对 [1,5] 采样),组合起来便有 10 种概率相同的结果,把这些结果映射到 [1,10] 即可。 |
| 528. 按权重随机选择 medium |
给定一个正整数数组,其中每个元素代表该元素下标的权重;按权重随机地选出一个下标。 | 存储数组的前缀和,每当需要采样时,先随机产生一个数字,然后使用二分法查找其在前缀和中的位置,以模拟加权采样的过程。 |
(5)脑筋急转弯
| 题目 | 题干 | 解法 |
|---|---|---|
| 22. 括号生成 medium |
数字n代表生成括号的对数,设计一个函数生成所有可能的并且有效的括号组合。 | 考虑到在任意位置插入括号都可以等价于插入一个连续的’()’,因此递归地在n-1对括号中插入一对新的括号。 |
| 134. 加油站 medium |
在一条环路上有n个加油站,其中第i个加油站有汽油gas[i]升。有一辆油箱容量无限的的汽车,从第i个加油站开往第i+1个加油站需要消耗汽油cost[i]升。从其中的一个加油站出发,如果可以按顺序绕环路行驶一周,则返回出发时加油站的编号。 | 从每个加油站出发模拟整个环路。注意到若从加油站i出发最远可达加油站j,则从两个加油站之间的任意加油站z出发,最远也只可达加油站j;根据该结论,在遍历时可以跳过一些加油站。 |
| 292. Nim 游戏 easy |
桌子上有一堆石头。你们轮流进行自己的回合,你作为先手。每一回合,轮到的人拿掉1 - 3块石头。拿掉最后一块石头的人就是获胜者。 | 容易写出动态规划的转移方程\(dp[i] = \tilde{dp} [i-1]\text{ or }\tilde{dp}[i-2] \text{ or }\tilde{dp}[i-3]\),进一步发现状态按照TTTF循环,即只要石头不是$4$的倍数就能赢。 |
| 822. 翻转卡片游戏 medium |
有N张卡片,每张卡片的正面和背面都写着一个正数。可以先翻转任意张卡片,然后选择其中一张卡片。如果选中的那张卡片背面的数字与任意一张卡片的正面的数字都不同,那么这个数字是我们想要的数字。找到这些数中的最小值。 | 如果一张卡片正面和背面的数字相同,则该数字不满足条件;否则对于任意一面的数字,总可以翻转到背面,并把其余正面出现的该数字也翻转到背面。 |
| 870. 优势洗牌 medium |
给定两个大小相等的数组,返回数组1的任意排列,使其相对于数组2的优势最大化(满足数组1[i] > 数组2[i] 的索引 i 最大化)。 | 田忌赛马:用数组1的最小值匹配数组2的最小值;需对数组1以及数组2的下标按数值排序。 |
二、数据结构篇
数据结构可以用来实现各种算法,因此必须熟悉各种数据结构的特点。
⚪ 字符串
字符串是由字符组成的数组。由于字符串是程序里经常需要处理的数据类型,因此有很多针对字符串处理的题目。
有时需要进行字符的数值运算,可以通过ord()函数把它们转换成ASCII码后再计算:
ord('z') - ord('a') # 25
(1)字符串理解
字符串理解是指按要求处理给定的单个字符串。
寻找字符串中的回文子串通常采用中心扩展算法,枚举所有的「回文中心」(字符串的每个位置),并尝试「扩展」(向左向右延长),直到无法扩展为止(不再满足回文条件)。需要注意回文串长度有奇数和偶数两种情况,需要分开讨论。
n = len(s)
for i in range(n):
# 奇数情况
l, r = i-1, i+1
while l>=0 and r<n:
if s[l] == s[r]:
l -= 1
r += 1
else:
break
# s[l+1:r]是一个长度为r-l-1的回文子串
# 偶数情况
l, r = i-1, i
while l>=0 and r<n:
if s[l] == s[r]:
l -= 1
r += 1
else:
break
# s[l+1:r]是一个长度为r-l-1的回文子串
| 题目 | 题干 | 解法 |
|---|---|---|
| 3. 无重复字符的最长子串 medium |
给定一个字符串,找出其中不含有重复字符的最长子串的长度。 | 使用滑动窗口枚举不含重复字符的子串,使用哈希集合判断是否有重复的字符。 |
| 5. 最长回文子串 medium |
给定一个字符串,找出其中最长的回文子串。 | 计算以每个位置为回文中心的回文串的长度。 |
| 227. 基本计算器 II medium |
给定一个由整数和算符(加减乘除)组成的字符串表达式,实现一个基本计算器来计算并返回它的值。 | 由于乘除优先于加减计算,对于加减号后的数字,将其直接压入一个栈中;对于乘除号后的数字,可以直接与栈顶元素计算,并替换栈顶元素为计算后的结果。 |
| 409. 最长回文串 easy |
给定一个包含大写字母和小写字母的字符串,返回通过这些字母构造成的最长的回文串。 | 将每个字符使用偶数次,如果有剩余的字符,再取出一个作为回文中心。 |
| 647. 回文子串 medium |
给定一个字符串,统计这个字符串中回文子串的数目。回文字符串是正着读和倒过来读一样的字符串。 | 从字符串的每个位置开始,向左向右延长,判断存在多少以当前位置为中轴(分别考虑奇数和偶数长度)的回文子字符串。 |
| 696. 计数二进制子串 easy |
给定一个字符串,统计具有相同数量0和1的连续子字符串的数量,这些子字符串中的所有0和所有1都是成组连续的。 | 将字符串按照0和1的连续段分组,遍历所有相邻的数对,对应$u$个0和$v$个1,能组成的满足条件的子串数目为$\min(u,v)$。 |
| 722. 删除注释 medium |
给一个 C++ 程序,删除程序中的注释。字符串//表示行注释,表示//和其右侧的其余字符应该被忽略。字符串/* 表示一个块注释,它表示直到下一个(非重叠)出现的*/之间的所有字符都应该被忽略。 | 每个字符有两种情况,要么在一个注释内要么不在。遇到\(\text{`//'}\)直接忽略该行后面的部分;遇到\(\text{`/*'}\)将状态改为在注释块内,继续遍历后面第三个字符;遇到其他字符,记录该字符;在注释块内遇到\(\text{`*/'}\)将状态改为不在注释块内,继续遍历后面第三个字符。 |
| 833. 字符串中的查找与替换 medium |
对一个字符串执行k个替换操作。替换操作以三个长度均为k的并行数组给出:indices, sources, targets。要完成第 i 个替换操作:检查子字符串sources[i]是否出现在原字符串的索引indices[i]处。如果没有出现,什么也不做。如果出现,则用targets[i]替换该子字符串。 | 使用哈希存储索引-匹配子串和索引-替换子串,并模拟字符串中的替换过程。 |
| 1156. 单字符重复子串的最大长度 medium |
给定一个字符串,只能交换其中两个字符一次或者什么都不做,然后得到一些单字符重复的子串。返回其中最长的子串的长度。 | 计算以当前字符为开头的最长长度。$L_1$为当前重复子串长度,$L_2$为跳过一个字符后同一字符重复子串长度,若$L_1+L_2$小于该字符总数,则长度为$L_1+L_2+1$(把一个其他位置的字符替换到跳过的位置);否则长度为$L_1+L_2$(把一个第二个重复子串末尾替换到跳过的位置) |
| 1451. 重新排列句子中的单词 medium |
句子是一个用空格分隔单词的字符串。给定一个满足下述格式的句子: 句子的首字母大写;句子中的每个单词都用单个空格分隔。重新排列句子中的单词,使所有单词按其长度的升序排列。 | 通过chr()和ord()实现大小写转换,通过.split()和.join()实现字符串与数组的转换,通过.sort()重新排序。 |
(2)字符串比较
字符串比较是指按要求比较给定的两个或多个字符串。
| 题目 | 题干 | 解法 |
|---|---|---|
| 165. 比较版本号 medium |
给定两个版本号,版本号由一个或多个修订号组成,各修订号由一个’.’连接。每个修订号由多位数字组成,可能包含前导零。请按从左到右的顺序依次比较它们的修订号。 | 对两个字符串按’.’分割后依次比较整数值大小,需要考虑长度的对齐。 |
| 205. 同构字符串 easy |
给定两个字符串s和t,判断它们是否是同构的。如果s中的字符可以按某种映射关系(不同字符不能映射到同一个字符上,相同字符只能映射到同一个字符上,字符可以映射到自己本身)替换得到t,那么这两个字符串是同构的。 | 维护两张哈希字典,第一张哈希表以s中字符为键,映射至t的字符为值;第二张哈希表以t中字符为键,映射至s的字符为值。 |
| 242. 有效的字母异位词 easy |
给定两个字符串s和t,判断t是否是s的字母异位词。若s和t中每个字符出现的次数都相同,则称s和t互为字母异位词。 | 用哈希表或者数组统计两个数组中每个数字出现的频次,若频次相同,则说明它们包含的字符完全相同。 |
| 524. 通过删除字母匹配到字典里最长单词 medium |
给定一个字符串$s$和一个字符串数组,从数组中找出可以通过删除$s$中的某些字符得到的长度最长的字符串。 | 对字符串数组依据字符串长度的降序和字典序的升序进行排序,然后使用双指针模拟字符串匹配过程。 |
⚪ 基本数据结构
(1)数组 array
数组是最常用的数据结构之一,在python中体现为列表list。
| 题目 | 题干 | 解法 |
|---|---|---|
| 31. 下一个排列 medium |
整数数组的下一个排列是指其整数的下一个字典序更大的排列。给定一个整数数组,找出下一个排列。 | 先从后往前找出一个较小值$a_i$(满足$a_i < a_{i+1}$),再从$[i+1,n)$中找出一个尽可能小的较大值$a_j=\min_{a_k > a_i}a_k$,交换$a_i,a_j$使得数组字典序变大,并把$[i+1,n)$调整为递增使得变大的字典序尽可能小。 |
| 48. 旋转图像 medium |
把一个 n × n 的二维矩阵顺时针旋转 90 度,需要直接修改输入的二维矩阵。 | 解法①:每一次原地交换四个位置,对应索引的赋值关系: \(\begin{aligned} &(i,j) \to (j,n-i-1) \\ &(j,n-i-1) \to (n-i-1,n-j-1) \\ &(n-i-1,n-j-1) \to (n-j-1,i) \\ &(n-j-1,i) \to (i,j) \\ & i\in [0, n//2) , j\in [0, (n+1)//2) \end{aligned}\) 解法②:水平轴翻转+主对角线翻转(转置) \((i,j) \to (n-i-1,j) \to (j,n-i-1)\) |
| 53. 最大子数组和 medium |
找出一个整数数组中具有最大和的连续子数组,返回其最大和。 | 状态定义:$dp[i]$为以第$i$个元素为结尾的子数组的最大和 转移方程:\(dp[i] = \max(dp[i-1], 0) + alist[i]\) 边界条件:\(dp[1]=alist[0]\) 返回值:\(\max(dp)\) 空间压缩:使用长度为1的滚动数组 |
| 54. 螺旋矩阵 medium |
给定一个矩阵,按照顺时针螺旋顺序返回矩阵中的所有元素。 | 使用一个向量模拟顺序$(0,1)\to(1,0)\to(0,-1)\to(-1,0)$对矩阵进行螺旋遍历。 |
| 59. 螺旋矩阵 II medium |
给定一个正整数$n$,生成一个包含$1$到$n^2$所有元素,且元素按顺时针顺序螺旋排列的$n \times n$正方形矩阵。 | 使用一个向量模拟顺序对矩阵进行填充。 |
| 189. 轮转数组 medium |
给定一个整数数组,将数组中的元素向右轮转k个位置。 | 若想实现”—–>–>“到”–>—–>“,不妨先全局翻转实现”<–<—–“,再分别翻转两个子数组。 |
| 240. 搜索二维矩阵 II medium |
搜索二维矩阵中的一个目标值。该矩阵每行的元素从左到右升序排列,每列的元素从上到下升序排列。 | 从右上角开始查找,若当前值大于待搜索值,向左移动一位;若当前值小于待搜索值,向下移动一位。若坐标越界则说明待搜索值不存在于矩阵中。 |
| 287. 寻找重复数 medium |
给一个含 n+1 个整数的数组,其数字在 [1, n] 范围内,假设数组只有一个重复的整数,返回这个重复的数。 | 鸽笼原理:把出现的数字在原数组出现的位置设为负数。 |
| 448. 找到所有数组中消失的数字 easy |
给一个含 n 个整数的数组,找出所有在 [1, n] 范围内但没有出现在数组中的数字。 | 鸽笼原理:把重复出现的数字在原数组出现的位置设为负数,最后仍然为正数的位置即为没有出现过的数。 |
| 498. 对角线遍历 medium |
给定一个矩阵,以对角线遍历的顺序,用一个数组返回这个矩阵中的所有元素。 | 使用一个向量模拟顺序$(-1,1)\to(1,-1)$对矩阵进行对角线遍历。 |
| 566. 重塑矩阵 easy |
把一个 $m\times n$ 矩阵重塑为另一个大小不同($r \times c$)的新矩阵。 | 对于矩阵中第$x \in [0,mn)$个元素: \(mat2[x//c,x\%c] = mat1[x//n,x\%n]\) |
| 769. 最多能完成排序的块 medium |
给定一个在 [0, n - 1] 范围内的整数的排列。返回数组能分成的最多块数量,使得对每个块单独排序并连接起来后,结果和按升序排序后的原数组相同。 | 从左往右遍历,同时记录当前的最大值,每当当前最大值等于数组位置时,可以多一次分割。 |
| 918. 环形子数组的最大和 medium |
给定一个环形整数数组,返回非空子数组的最大可能和。环形数组意味着数组的末端将会与开头相连呈环状。 | 若最大和子数组是连续的,则问题等价为“53. 最大子数组和”。若最大和子数组不连续(左端+右端),则通过动态规划定义$dp[i]$为前$i$个元素中左端子数组的最大和,状态转移方程$dp[i] = \max(dp[i-1], sum(nums[0:i+1]))$,全局子数组和表示为$\max_j dp[j-1] + sum(nums[j:])$。 |
| 1253. 重构 2 行二进制矩阵 medium |
给定一个2行n列的二进制数组,第0行的元素之和为upper。第1行的元素之和为lower。第i列的元素之和为colsum[i]。利用upper,lower和colsum来重构这个矩阵。 | 贪心:$[1,1]^T$出现次数为$t=colsum.count(2)$,$[1,0]^T$出现次数为$upper-t$,$[0,1]^T$出现次数为$lower-t$。 |
| 1267. 统计参与通信的服务器 medium |
服务器的位置标识在整数矩阵网格中。如果两台服务器位于同一行或者同一列,认为它们之间可以进行通信。统计能够与至少一台其他服务器进行通信的服务器的数量。 | 第一次遍历累计每一行和每一列出现的服务器数量,第二次遍历检查该行或列是否出现至少两个服务器。 |
| 1375. 二进制字符串前缀一致的次数 medium |
给定范围 $[1, n]$ 中所有整数构成的一个排列,按排列顺序依次翻转全$0$二进制字符串的每一位。返回二进制字符串在翻转过程中前缀一致的次数。二进制字符串前缀一致需满足在区间 $[1, i]$ 内的所有位都是$1$,而其他位都是$0$。 | 解法同“769. 最多能完成排序的块”。 |
| 1921. 消灭怪物的最大数量 medium |
给定一个整数数组表示怪物与城市的初始距离,和一个整数数组表示每个怪物的速度。可以在每一分钟的开始时消灭一个怪物,返回可以消灭的怪物的最大数量。 | 计算每个怪物到达城市的时刻(向上取整)并排序,可以被消灭的怪物满足:第$i$个怪物到达城市的时间大于$i$。 |
| 2475. 数组中不等三元组的数目 easy |
给定一个正整数数组,统计数值互不相同的三元组的数目。 | 对数组进行排序后,以某一堆相同的数$[i,j)$作为三元组的中间元素,能产生三元组的数目为$i\times (j-i) \times (n-j)$ |
(2)栈和队列 Stack and Queue
栈是一种后入先出(last in first out, LIFO)的数据结构,常用于深度优先搜索、一些字符串匹配问题以及单调栈问题。队列是一种先入先出(first in first out, FIFO)的数据结构,常用于广度优先搜索。
栈和队列在python中都可以用列表list实现;为了实现$O(1)$的头部增删和尾部增删,默认基于双端队列collections.deque实现。
from collections import deque
stack = deque([])
stack.append()
stack.pop()
queue = deque([])
queue.append()
queue.popleft()
| 题目 | 题干 | 解法 |
|---|---|---|
| 20. 有效的括号 easy |
给定一个只包括 ‘(‘,’)’,’{‘,’}’,’[‘,’]’ 的字符串,判断字符串是否有效。 | 从左往右遍历:每当遇到左括号便放入栈内;遇到右括号则判断其和栈顶的括号是否是统一类型,是则从栈内取出左括号,否则说明字符串不合法。 |
| 32. 最长有效括号 hard |
给定一个只包括 ‘(‘,’)’的字符串,找出最长有效(格式正确且连续)括号子串的长度。 | 从左往右遍历:每当遇到左括号便把其下标入栈;遇到右括号时若栈内存在左括号,则出栈并更新当前有效括号长度(当前下标减去栈顶元素),否则把右括号的下标入栈。 |
| 155. 最小栈 medium |
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。 | 额外建立一个新栈,栈顶表示原栈里所有值的最小值。 |
| 225. 用队列实现栈 easy |
仅使用两个队列实现后入先出栈。栈应当支持一般栈支持的所有操作(push、pop、top、empty)。 | 使用列表模拟队列,在取值时通过一个额外队列翻转一次数组。 |
| 232. 用栈实现队列 easy |
仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty)。 | 使用列表模拟栈,在取值时通过一个额外栈翻转一次数组。 |
| 1190. 反转每对括号间的子串 medium |
给定一个字符串(仅含有小写英文字母和括号),按照从括号内到外的顺序,逐层反转每对匹配括号中的字符串。 | 通过栈匹配每对括号,并反转括号中间的子串。 |
(3)单调栈
单调栈通过维持栈内值的单调递增(递减)性,在整体 $O(n)$ 的时间内处理需要大小比较的问题。
单调栈经常被用于寻找数组中当前位置对应的下一个更大/小值,此时可以维护一个存储下标的单调递减/递增栈。以寻找更大值为例,维持一个存储下标的单调递减栈,每次有下标进栈时,会将对应数值更小的下标全部出栈,并更新这些下标对应的下一个更大值;同时,栈顶元素也记录了该下标对应的上一个更大值(或相等值):
stack = []
for i in range(n):
while stack and nums[stack[-1]] < nums[i]:
idx = stack.pop()
nextMaxVal[idx] = nums[i]
prevMaxVal[idx] = stack[-1]
stack.append(i)
| 题目 | 题干 | 解法 |
|---|---|---|
| 42. 接雨水 hard |
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 | 考察以每个数值作为底能接到的雨水数。使用单调递减栈寻找下一个更大值和上一个更大值,并累计雨水。 |
| 84. 柱状图中最大的矩形 hard |
给定 n 个非负整数表示柱状图中各个柱子的高度,求该柱状图中能够勾勒出来的矩形的最大面积。 | 考察以每个数值作为高度的最大矩形面积。使用单调递增栈寻找下一个更小值和上一个更小值;需要先在数组前后补零。 |
| 85. 最大矩形 hard |
给定一个仅包含0和1的二维二进制矩阵,找出只包含1的最大矩形,并返回其面积。 | 首先统计矩阵的每个元素及其左边连续1的数量,则对于统计矩阵的每一列可以看作一个柱状图,问题转换为求每个柱状图的最大面积,等价于“84. 柱状图中最大的矩形”。 |
| 496. 下一个更大元素 I easy |
给定一个数组,返回数组的一个子集中每个元素在原数组中的下一个更大元素。 | 使用单调递减栈寻找下一个更大值,并将对应关系存储为哈希表。 |
| 503. 下一个更大元素 II medium |
给定一个循环数组,返回数组中每个元素的下一个更大元素。 | 使用单调递减栈寻找下一个更大值;对于第一次遍历没有找到对应更大值的下标,再进行第二次遍历,此时只出栈。 |
| 739. 每日温度 medium |
给定一个整数数组表示每天的温度,返回一个数组,其中第i个元素是指对于第i天,下一个更高温度出现在几天后。 | 使用单调递减栈寻找下一个更大值,并更新出栈下标对应的等待天数。 |
(4)优先队列(堆)
优先队列 (priority queue) 是一种最大值(或最小值)先出的数据结构。它可以在$O(n \log n)$的时间排序数组,$O(1)$的时间获得最大值,$O(\log n)$的时间插入任意值或删除最大值。优先队列常用于维护数据结构并快速获取最大或最小值。
优先队列是通过堆(queue)这种数据结构实现的。python中的heapq库提供了优先队列的基本操作,相当于最小堆:
import heapq
queue = []
# 注意 Python 默认的优先队列是最小堆
heapq.heappush(queue, elem) # 添加元素
minVal = heapq.heappop(queue) # 弹出最小元素
queue.remove(elem) # 删除任意元素
heapq.heapify(queue) # 删除后要恢复堆的性质
| 题目 | 题干 | 解法 |
|---|---|---|
| 23. 合并 K 个升序链表 hard |
给定一个链表数组,每个链表都已经按升序排列,将所有链表合并到一个升序链表中。 | 使用最小堆维护当前每个链表没有被合并的元素的最前面一个,每次在这些元素里面选取最小的元素合并到答案中。 |
| 218. 天际线问题 hard |
城市的天际线是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。给出所有建筑物的位置和高度,请返回由这些建筑物形成的天际线。 | 存储建筑物的端点和高度,依次按照端点大小、左端点、较大高度排序。然后依次读取端点和高度:如果是左端点,说明存在一条往右延伸的可记录的边,将高度存入最大堆;如果是右端点,说明这条边结束了,将当前高度从最大堆中移除。取出最高高度,如果当前不与前一矩形“上边”延展而来的那些边重合,则可以被记录。 |
| 239. 滑动窗口最大值 hard |
给定一个整数数组,有一个滑动窗口从数组的最左侧移动到数组的最右侧,记录在每个位置的滑动窗口中的最大值。 | 每次向右移动窗口时,把新的元素及其索引放入最大堆中。然后不断地移除堆顶不在窗口范围内的元素,直到其确实出现在滑动窗口中。 |
| 264. 丑数 II medium |
给定一个整数n,找出第n个丑数,丑数是只包含质因数 2、3 和/或 5 的正整数。 | 维护一个最小堆,每次取出堆顶元素$x$,则$2x,3x,5x$也是丑数;为了避免重复元素,使用哈希集合去重。 |
| 373. 查找和最小的 K 对数字 medium |
给定两个以升序排列的整数数组,找到和最小的k个数对,数对中的元素分别来自两个数组。 | 维护一个最小堆,每次取出和最小的数对$(i,j)$,并把数对$(i+1,j)$和$(i,j+1)$加入堆;注意需要去重。 |
| 1439. 有序矩阵中的第 k 个最小数组和 hard |
给定一个矩阵,矩阵中的每一行都以非递减的顺序排列。从每一行中选出1个元素形成一个数组。返回所有可能数组中的第k个最小数组和。 | 题目“373. 查找和最小的 K 对数字”的扩展。维护一个最小堆,每次取出和最小的数组,并把其索引数组的每一项加1后加入堆;注意需要去重。 |
| 1499. 满足不等式的最大值 hard |
给定一个数和一个整数k。数组中每个元素[xi, yi]都表示二维平面上的点的坐标,并按照横坐标的值从小到大排序。找出yi + yj + |xi - xj|的最大值,且|xi - xj| <= k。 | 题干等价于求最大的xj+yj+(yi-xi), j>i;使用最大堆维护yi-xi,遍历二维坐标,对每个坐标[xj, yj]丢弃最大堆中|xi - xj| > k的点,通过堆顶元素计算局部最大目标。 |
| 1851. 包含每个查询的最小区间 hard |
给定一个区间数组和一个查询数组,第i个查询整数的答案是包含该整数的区间的最小长度。以数组形式返回对应查询的所有答案。 | 首先对两个数组进行排序(采用离线查询模式)。对每个查询,维护一个包含左端点不大于该数的区间的长度的最小堆;该查询的答案是堆顶包含该数的区间长度。 |
| 2208. 将数组和减半的最少操作次数 medium |
给定一个正整数数组。每一次操作可以从中选择任意一个数并将它减小到恰好一半。返回将数组和至少减少一半的最少操作数。 | 把数组维护成最大堆,每次取出最大元素并减小一半。 |
| 2679. 矩阵中的和 medium |
给定一个二维整数数组。执行以下操作直到矩阵变为空:矩阵中每一行选取最大的一个数,并删除它。在删除的所有数字中找到最大的一个数字,添加到分数中。返回最后的分数。 | 把数组每一行维护成最大堆,然后模拟元素取出过程。 |
(5)哈希表(字典和集合)
哈希表 (hash)又称散列表,使用 $O(n)$ 空间复杂度存储数据,通过哈希函数映射位置,从而实现近似 $O(1)$ 时间复杂度的插入、查找、删除等操作。
python提供了字典dict和集合set数据结构作为哈希表,可以用来统计频率,记录内容等等。有时需要为不存在的键设置默认值,也可以用collections.defaultdict实现。
from collections import defaultdict
dd = defaultdict(lambda: 0) # 设置value的默认值为0
| 题目 | 题干 | 解法 |
|---|---|---|
| 1. 两数之和 easy |
给定一个整数数组和一个整数目标值,在数组中找出和为目标值的两个整数。 | 用字典存储遍历过的值以及它们的位置,每次遍历到新的位置时,查找字典里是否存在满足求和条件的值。 |
| 49. 字母异位词分组 medium |
给定一个字符串数组,将字母异位词组合在一起。字母异位词是由重新排列源单词的所有字母得到的一个新单词。 | 用字典存储字母异位词,键可以通过单词排序或把单词编码为长度26的数组构造。 |
| 128. 最长连续序列 medium |
给定一个未排序的整数数组,找出数字连续的最长序列的长度。 | 用字典存储数组中的值,搜索每个连续序列的起点,并记录它们的最大连续长度。 |
| 217. 存在重复元素 easy |
给定一个整数数组,判断是否存在任一值在数组中出现至少两次。 | 使用集合去重。 |
| 594. 最长和谐子序列 easy |
和谐数组是指一个数组里元素的最大值和最小值之间的差别正好是 1 。给定一个整数数组,在所有可能的子序列中找到最长的和谐子序列的长度。 | 使用字典存储每个数出现的频数。 |
| 697. 数组的度 easy |
给定一个非空且只包含非负数的整数数组,数组的度的定义是指数组里任一元素出现频数的最大值。在数组中找到与数组拥有相同大小的度的最短连续子数组,返回其长度。 | 使用字典存储每个数出现的频数、首次出现位置和最后出现位置。寻找度最大的元素中最接近的起止位置。 |
⚪ 基于指针的数据结构
(1)链表
(单)链表是由节点和指针构成的数据结构,每个节点存有一个值,和一个指向下一个节点的指针。
不同于数组,链表并不能直接获取任意节点的值,必须要通过指针找到该节点后才能获取其值。同理,在未遍历到链表结尾时,我们也无法知道链表的长度,除非依赖其他数据结构储存长度。LeetCode 默认的链表表示方法如下。
# Definition for singly-linked list.
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
由于在进行链表操作时,尤其是删除节点时,经常会因为对当前节点进行操作而导致内存或指针出现问题。有两个小技巧可以解决这个问题:一是尽量处理当前节点的下一个节点而非当前节点本身,二是建立一个哑节点 (dummy node),使其指向当前链表的头节点,这样即使原链表所有节点全被删除,也会有一个 dummy 存在,返回 dummy.next 即可。
建立哑节点:
dummy = ListNode(0)
dummy.next = head
# 处理链表
return dummy.next
很多链表问题可以用递归来处理,比如递归提供了一种优雅的方式来反向遍历节点。
def reverse_node(head):
if not head:
return
reverse_node(head.next)
return head.val
值得一提的是,在许多语言中,递归堆栈帧的开销很大(如 Python),并且最大的运行时堆栈深度为 $1000$(可以增加,但是有可能导致底层解释程序内存出错)。为每个节点创建堆栈帧极大的限制了算法能够处理的最大链表大小。
| 题目 | 题干 | 解法 |
|---|---|---|
| 19. 删除链表的倒数第 N 个结点 medium |
给定一个链表,删除链表的倒数第n个结点。 | 先后指针:使用两个指针 first 和 second 同时对链表进行遍历,并且 first 比 second 超前 n 个节点。当 first 遍历到链表的末尾时,second 就恰好处于倒数第 n 个节点。 |
| 21. 合并两个有序链表 easy |
将两个升序链表合并为一个新的升序链表并返回。 | 解法①:迭代,使用一个哨兵节点存储当前较小的节点 解法②:递归,问题拆分成当前较小节点+合并下一个节点指向的链表和另一个链表,终止条件为至少有一个链表为空 |
| 24. 两两交换链表中的节点 medium |
给定一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。 | 解法①:迭代,使用两个指针分别存储前一个和后一个节点 \(\begin{aligned} pre &= dummy \\ pre.next &= head.next \\ next &= head.next.next \\ head.next.next &= head \\ pre &= head \\ head.next & = next \\ head &= head.next \end{aligned}\) 解法②:递归,问题拆分成前两个节点+第三个节点指向的链表,终止条件为空或者单节点 |
| 25. K 个一组翻转链表 hard |
给定链表的头节点,每k个节点一组进行翻转,返回修改后的链表。如果节点总数不是k的整数倍,请将最后剩余的节点保持原有顺序。 | 递归,问题拆分成翻转当前k个节点+递归地翻转后续节点。 |
| 83. 删除排序链表中的重复元素 easy |
给定一个已排序的链表的头节点,删除所有重复的元素,使每个元素只出现一次。 | 比较当前节点和下一个节点的数值:若相等则跳过下一个节点,否则指向下一个节点。 |
| 92. 反转链表 II medium |
给定单链表的头节点和两个整数$l,r$,反转从位置$l$到位置$r$的链表节点。 | 先定位到第$l$个节点,并反转后面的子链表的前$r-l+1$个节点。 |
| 148. 排序链表 medium |
给定链表的头节点,将其按升序排列并返回排序后的链表。 | 利用快慢指针找到链表中点后,可以对链表进行归并排序。 |
| 160. 相交链表 easy |
给定两个单链表的头节点,找出两个单链表相交的起始节点。 | 双指针:创建两个指针初始时分别指向两个链表的头节点,然后将两个指针依次遍历两个链表的每个节点,如果指针为空则指向另一个链表的头节点,最后两个指针会指向同一个节点或者都为空。 |
| 203. 移除链表元素 easy |
给定一个链表的头节点和一个整数,删除链表中所有满足值等于该整数的节点,并返回新的头节点。 | 处理当前节点的下一个节点,若需要删除则跳过该节点,否则移动指针。 |
| 206. 反转链表 easy |
给定单链表的头节点,反转链表并返回。 | 解法①:迭代,使用两个指针分别存储前一个和后一个节点 \(\begin{aligned} next &= head.next \\ head.next &= next.next \\ next.next &= dummy.next \\ dummy.next &= next \end{aligned}\) 解法②:递归,问题拆分成第一个节点+第二个节点指向的链表,终止条件为空或者单节点 |
| 234. 回文链表 easy |
给定一个单链表的头节点,判断该链表是否为回文链表。 | 解法①:先使用快慢指针找到链表中点,再把链表切成两半;然后把后半段翻转;最后比较两半是否相等。 解法②:递归,使用递归反向迭代节点,同时使用递归函数外的变量向前迭代,匹配两者的数值。 |
| 328. 奇偶链表 medium |
给定单链表的头节点,将所有索引为奇数的节点和索引为偶数的节点分别组合在一起,然后返回重新排序的列表。 | 将奇数节点和偶数节点分离成奇数链表和偶数链表,然后将偶数链表连接在奇数链表之后,合并后的链表即为结果链表。 |
| 708. 循环有序列表的插入 medium |
给定循环单调非递减列表中的一个点,向这个列表中插入一个新元素,使这个列表仍然是循环升序的。 | 考虑若干特殊情况:空链表、只有单个节点、所有节点数值相同。 |
(2)树
树是单链表的升级版,如无特别说明,本文主要讨论二叉树(binary tree),即每个节点最多有两个子节点;其与链表的主要差别就是多了一个子节点的指针。LeetCode 默认的树表示方法如下。
# Definition for a binary tree node.
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
⚪ 树的递归
树的递归是指首先处理以当前节点为根节点的树,再递归地处理左右子树;其写法与深度优先搜索的递归写法相同。
| 题目 | 题干 | 解法 |
|---|---|---|
| 101. 对称二叉树 easy |
给定一个二叉树的根节点,检查它是否轴对称。 | 递归:判断一个树是否对称等价于判断左右子树是否对称。(1)如果两个子树都为空指针,则它们相等或对称;(2)如果两个子树只有一个为空指针,则它们不相等或不对称;(3)如果两个子树根节点的值不相等,则它们不相等或不对称(4)根据相等或对称要求,进行递归处理。 |
| 104. 二叉树的最大深度 easy |
给定一个二叉树,找出其最大深度。二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。 | 深度搜索遍历二叉树时传递当前最大深度。 |
| 110. 平衡二叉树 easy |
给定一个二叉树,判断它是否是高度平衡的二叉树。一棵高度平衡二叉树定义为:一个二叉树每个节点的左右两个子树的高度差的绝对值不超过1。 | 解法①:自顶向下的递归(前序遍历),先判断以当前节点为根结点的二叉树是否平衡,再判断左子树和右子树是否平衡。 解法②:自底向上的递归(后序遍历),先递归地判断其左右子树是否平衡,再判断以当前节点为根的子树是否平衡。 |
| 112. 路径总和 easy |
给定一个二叉树和一个表示目标和的整数。判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。 | 传递根节点到当前节点的路径和,若当前节点为叶子节点,则进行判断。 |
| 124. 二叉树中的最大路径和 hard |
给定一个二叉树,找出其最大路径和。二叉树中的路径被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。 | 深度搜索遍历二叉树时传递以当前节点为起点的最大路径和f(node)=node.val+max(0,f(node.left),f(node.right)),并更新全局最大路径和ans=max(ans,f(node.left),f(node.right),f(node),f(node.left)+f(node.right)+node.val)。 |
| 226. 翻转二叉树 easy |
给定一个二叉树的根节点,翻转这棵二叉树,并返回其根节点。 | 递归地翻转左右子树,再交换两棵子树的位置。 |
| 236. 二叉树的最近公共祖先 medium |
给定一个二叉树,找到该树中两个指定节点的最近公共祖先。 | 最近公共祖先应满足:左右子树分别包含一个指定节点或根结点为其中一个节点。递归地判断左右子树是否包含指定节点。 |
| 257. 二叉树的所有路径 easy |
按任意顺序返回二叉树所有从根节点到叶子节点的路径。 | 使用深度优先搜索,遍历树的所有节点,传递当前路径。 |
| 404. 左叶子之和 easy |
给定一个二叉树的根节点,返回所有左叶子之和。 | 深度遍历二叉树时传递一个表示是否为左节点的布尔值。 |
| 437. 路径总和 III medium |
给定一个二叉树的根节点和一个整数,求该二叉树里节点值之和等于该整数的路径的数目。 | 解法①:前序遍历,先计算从当前节点出发的路径中满足条件的数量,再计算从左子树和右子树出发的路径树。 解法②:使用前缀和哈希记录由根结点到当前结点的路径上所有节点的和;对于当前节点,路径数目为当前节点值减去目标值对应的哈希值;退出当前节点时需要移除当前前缀和。 |
| 543. 二叉树的直径 easy |
给定一个二叉树,计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。 | 递归地计算左右子节点的最大深度。 |
| 572. 另一棵树的子树 easy |
给定两棵二叉树 root 和 subRoot,检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。 | 判断当前节点是否指向subRoot,然后递归地检查左右子节点。 |
| 617. 合并二叉树 easy |
给定两棵二叉树,将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则不为 null 的节点将直接作为新二叉树的节点。 | 合并当前节点,然后递归地合并左右子树。 |
| 865. 具有所有最深节点的最小子树 medium |
给定一个二叉树,每个节点的深度是该节点到根的最短距离。返回包含原始树中所有最深节点的最小子树 。 | 首先找到所有具有最大深度的叶节点集合,则问题转化为“236. 二叉树的最近公共祖先”。 |
| 979. 在二叉树中分配硬币 medium |
给定二叉树的根节点,树中的每个结点上都对应有硬币。可以选择两个相邻的结点,然后将一枚硬币从其中一个结点移动到另一个结点。返回使每个结点上只有一枚硬币所需的移动次数。 | 使用后序遍历的深度优先搜索返回每个结点应该向其父节点转移的硬币个数:为使左子树与右子树满足题意,左右子节点分别与该节点转移l和r个硬币,则该节点应该向其父节点转移l+r+node.val-1枚硬币。 |
| 1026. 节点与其祖先之间的最大差值 medium |
给定二叉树的根节点,找出存在于不同节点 A 和 B 之间的最大值 $abs(A.val-B.val)$,且 A 是 B 的祖先。 | 深度遍历二叉树时传递历史最大值与最小值。 |
| 1110. 删点成林 medium |
给定一个二叉树的根节点,树上每个节点都有一个不同的值,如果节点值在待删除数组中出现,就把该节点从树上删去,返回最后得到的森林(一些不相交的树构成的集合)。 | 对于每个待删除的节点,其左右子节点成为新的子树根节点候选,并将该节点与父节点的关系进行移除。 |
| 1367. 二叉树中的链表 medium |
给定一棵二叉树和一个链表。判断在二叉树中,是否存在一条一直向下的路径,且每个点的数值恰好一一对应链表中每个节点的值。 | 通过深度优先搜索判断以当前节点为头节点是否能够匹配链表,并递归地判断左右节点。 |
| 1448. 统计二叉树中好节点的数目 medium |
给定一棵二叉树,返回二叉树中好节点的数目。「好节点」定义为:从根到该节点所经过的节点中,没有任何节点的值大于该节点的值。 | 通过深度优先搜索判断当前节点的值是否不小于历史路径中节点的最大值。 |
| 剑指 Offer 26. 树的子结构 medium |
输入两棵二叉树A和B,判断B是不是A的子结构。 | 判断B的当前节点是否与A中的节点匹配,然后递归地检查左右子节点。 |
⚪ 树的前序遍历、中序遍历和后序遍历(深度优先搜索)
利用深度优先搜索遍历二叉树的方式有三种:前序遍历、中序遍历和后序遍历。它们对节点访问的顺序有一点不同,其它完全相同。
# 前序遍历先遍历根结点,再遍历左结点,最后遍历右节点
def preorder(root):
print(root.val)
preorder(root.left)
preorder(root.right)
# 对于任意一颗树而言,前序遍历的形式总是
# [ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] ]
# 中序遍历先遍历左节点,再遍历根结点,最后遍历右节点
def inorder(root):
inorder(root.left)
print(root.val)
inorder(root.right)
# 对于任意一颗树而言,中序遍历的形式总是
# [ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] ]
# 后序遍历先遍历左节点,再遍历右结点,最后遍历根节点
def postorder(root):
postorder(root.left)
postorder(root.right)
print(root.val)
# 对于任意一颗树而言,后序遍历的形式总是
# [ [左子树的中序遍历结果], [右子树的中序遍历结果], 根节点 ]
| 题目 | 题干 | 解法 |
|---|---|---|
| 94. 二叉树的中序遍历 easy |
给定一个二叉树的根节点,返回它节点值的中序遍历。递归算法很简单,你可以通过迭代算法完成吗? | 递归的本质是栈调用,可以通过栈来实现中序遍历。注意入栈的顺序先右再根后左,并优先读取没有子树可以入栈的节点。 |
| 105. 从前序与中序遍历序列构造二叉树 medium |
给定一个二叉树的前序遍历和中序遍历,构造二叉树并返回其根节点。 | 在前序遍历数组中从前往后依次取到根节点,对应的去中序数组中确定左子树和右子树的范围。 |
| 106. 从中序与后序遍历序列构造二叉树 medium |
给定一个二叉树的中序遍历和后序遍历,构造二叉树并返回其根节点。 | 在后序遍历数组中从后往前依次取到根节点,对应的去中序数组中确定左子树和右子树的范围。 |
| 114. 二叉树展开为链表 medium |
给定一个二叉树,将它展开为一个单链表,展开后的单链表应该与二叉树先序遍历顺序相同,并且不能创建新的节点。 | 首先存储二叉树前序遍历的节点列表,然后依次把列表的前一个节点指向下一个节点。 |
| 144. 二叉树的前序遍历 easy |
给定一个二叉树的根节点,返回它节点值的前序遍历。递归算法很简单,你可以通过迭代算法完成吗? | 递归的本质是栈调用,可以通过栈来实现前序遍历。注意入栈的顺序先右后左,保证左子树先遍历。 |
| 145. 二叉树的后序遍历 easy |
给定一个二叉树的根节点,返回它节点值的后序遍历。递归算法很简单,你可以通过迭代算法完成吗? | 递归的本质是栈调用,可以通过栈来实现后序遍历。注意入栈的顺序先根再右后左,并优先读取没有子树可以入栈的节点。 |
| 889. 根据前序和后序遍历构造二叉树 medium |
给定一个二叉树的前序遍历和后序遍历,构造二叉树并返回其根节点。 | 在前序遍历数组中从前往后依次取到根节点及左子节点,对应的去后序数组中确定左子树和右子树的范围。 |
⚪ 树的层次遍历(广度优先搜索)
可以使用广度优先搜索进行层次遍历。注意,不需要使用两个队列来分别存储当前层的节点和下一层的节点,因为在开始遍历一层的节点时,当前队列中的节点数就是当前层的节点数,只要控制遍历这么多节点数,就能保证这次遍历的都是当前层的节点。
from collections import deque
q = deque([root])
while q:
n = len(q)
# 处理该层的n个节点
for i in range(n):
node = q.popleft()
q.append(node.left)
q.append(node.right)
| 题目 | 题干 | 解法 |
|---|---|---|
| 101. 对称二叉树 easy |
给定一个二叉树的根节点,检查它是否轴对称。 | 迭代,引入一个队列,把根节点入队两次。每次提取两个结点并比较它们的值,然后将两个结点的左右子结点按相反的顺序插入队列中。当队列为空时,或者检测到树不对称时,该算法结束。 |
| 102. 二叉树的层序遍历 medium |
给定一个二叉树的根节点,返回其节点值的层序遍历。 | 使用广度优先搜索从左向右搜索,传递当前节点层数。 |
| 103. 二叉树的锯齿形层序遍历 medium |
给定一个二叉树的根节点,返回其节点值的锯齿形层序遍历。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。 | 使用广度优先搜索从左向右搜索,传递当前节点层数,交替地顺序或逆序存储每一层的节点值。 |
| 199. 二叉树的右视图 medium |
给定一个二叉树的根节点,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。 | 使用广度优先搜索从左向右搜索,存储每一层的最后一个节点值。 |
| 513. 找树左下角的值 medium |
给定一个二叉树的根节点,找出该二叉树的最底层最左边节点的值。 | 使用广度优先搜索从右向左搜索,访问到的最后一个元素即为所求。 |
| 637. 二叉树的层平均值 easy |
给定一个非空二叉树的根节点,以数组的形式返回每一层节点的平均值。 | 使用广度优先搜索累计每一层的平均值。 |
⚪ 二叉查找树
二叉查找树(Binary Search Tree, BST)又称为二叉搜索树,是一种特殊的二叉树:对于每个父节点,其左子节点的值小于等于父结点的值,其右子节点的值大于等于父结点的值。同时因为二叉查找树是有序的,对其中序遍历的结果即为排好序的数组。
因此对于一个二叉查找树,可以在 $O(n \log n)$ 的时间内查找一个值是否存在:从根节点开始,若当前节点的值大于查找值则向左下走,若当前节点的值小于查找值则向右下走。比如寻找二叉查找树中的最小元素对应的节点:
minNode = root
while minNode.left:
minNode = minNode.left
| 题目 | 题干 | 解法 |
|---|---|---|
| 96. 不同的二叉搜索树 medium |
给定一个整数n,求恰由n个节点组成且节点值从1到n互不相同的二叉搜索树有多少种。 | 解题思路:问题等价于求所有中序遍历为[1,…,n]的二叉树的数量;任选其中一个元素为根节点,则可以递归地构造左右子树。 状态定义:$dp[i]$为具有$i$个节点的二叉树的数量 转移方程:\(dp[i] = \sum_{1\leq k \leq i} dp[k-1]*dp[i-k]\) 边界条件:$dp[0]=1$ 返回值:$dp[n]$ |
| 98. 验证二叉搜索树 medium |
判断一个二叉树是否是一个有效的二叉搜索树。 | 判断中序遍历数组是否单调递增(可以通过栈模拟)。 |
| 99. 恢复二叉搜索树 medium |
给定二叉搜索树的根节点,该树中的恰好两个节点的值被错误地交换。请在不改变其结构的情况下恢复这棵树。 | 使用中序遍历二叉查找树,同时设置一个指针记录前一个遍历节点。如果当前节点大于前一个节点的值,说明需要调整次序。如果遍历整个序列过程中只出现了一次次序错误,则交换这两个相邻节点;否则交换两次次序错误的节点。 |
| 109. 有序链表转换二叉搜索树 medium |
给定一个单链表的头节点,其中的元素按升序排序,将其转换为高度平衡的二叉搜索树。 | 使用快慢指针搜索链表的中部(若为偶数长度则应取右节点),然后以中部节点为根节点,递归地构造左右子树。 |
| 235. 二叉搜索树的最近公共祖先 medium |
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。 | 最近公共祖先应满足:左右子树分别包含一个指定节点或根结点为其中一个节点。通过节点的数值关系判断最近公共祖先的位置。 |
| 449. 序列化和反序列化二叉搜索树 medium |
设计一个算法来序列化和反序列化二叉搜索树。 只需确保二叉搜索树可以序列化为字符串,并且可以将该字符串反序列化为最初的二叉搜索树。 | 存储前序遍历的结果,中序遍历可以通过前序遍历排序得到。通过前序和中序数组重构二叉搜索树。 |
| 450. 删除二叉搜索树中的节点 medium |
给定一个二叉搜索树的根节点和一个值,删除二叉搜索树中的该值对应的节点,并保证二叉搜索树的性质不变。 | 递归,分情况讨论: ① 当前节点的值大于目标值:递归左节点 ② 当前节点的值小于目标值:递归右节点 ③.I 当前节点的值等于目标值,且当前节点为叶节点:返回None ③.II 当前节点的值等于目标值,且当前节点不平衡:返回非空子树 ③.III 当前节点的值等于目标值,且当前节点平衡:将当前节点的后继节点(右子树中的最小节点)作为根节点,并从右子树中删除后继节点 |
| 530. 二叉搜索树的最小绝对差 easy |
给出一个二叉搜索树的根节点,返回树中任意两不同节点值之间的最小差值。 | 中序遍历,传递上一个节点的数值。 |
| 538. 把二叉搜索树转换为累加树 medium |
给出二叉搜索树的根节点,该树的节点值各不相同,将其转换为累加树,使每个节点的新值等于原树中大于或等于该节点值之和。 | 按照右→根→左的顺序遍历节点,传递当前累加值。 |
| 653. 两数之和 IV - 输入二叉搜索树 easy |
给定一个二叉搜索树和一个目标结果,判断二叉搜索树中是否存在两个元素的和等于给定的目标结果。 | 解法①:使用任意方法遍历节点,通过哈希集合存储已遍历的节点值。 解法②: 中序遍历把二叉树转化为有序数组,然后采用双指针搜索目标。 |
| 897. 递增顺序搜索树 easy |
给定二叉搜索树的根节点,按中序遍历将其重新排列为一棵递增顺序搜索树,使树中最左边的节点成为树的根节点,并且每个节点没有左子节点,只有一个右子节点。 | 中序遍历,使用哑节点记录根结点。 |
(3)图
图是树的升级版。图通常分为有向(directed)或无向(undirected),有循环(cyclic)或无循环(acyclic),所有节点相连(connected)或不相连(disconnected)。树即是一个相连的无向无环图,而另一种很常见的图是有向无环图(Directed Acyclic Graph,DAG)。
图通常有两种表示方法。假设图中一共有 $n$ 个节点、$m$ 条边。第一种表示方法是邻接矩阵(adjacency matrix):我们可以建立一个 $n× n$ 的矩阵 $G$,如果第 $i$ 个节点连向第 $j$ 个节点,则 $G[i][j]= 1$,反之为 $0$;如果图是无向的,则这个矩阵一定是对称矩阵,即 $G[i][j] = G[j][i]$。
第二种表示方法是邻接链表(adjacency list):我们可以建立一个大小为 $n$ 的数组,每个位置 $i$ 储存一个数组或者链表,表示第 $i$ 个节点连向的其它节点。
邻接矩阵空间开销比邻接链表大,但是邻接链表不支持快速查找 $i$ 和 $j$ 是否相连,因此两种表示方法可以根据题目需要适当选择。除此之外,我们也可以直接用一个 $m × 2$ 的矩阵储存所有的边。
# 构建无向图的邻接矩阵
graph = [[0]*n for _ in range(n)]
for a, b in edges:
graph[a][b] = 1
graph[b][a] = 1
# 构建无向图的邻接链表,适用于元素较多的场合
graph = [[] for _ in range(n)]
for a, b in edges:
graph[a].append(b)
graph[b].append(a)
| 题目 | 题干 | 解法 |
|---|---|---|
| 207. 课程表 medium |
总共有 n 门课需要选。给定一个数组,其中第i个元素[ai, bi]表示在选修课程 ai 前必须 先选修 bi。判断是否可能完成所有课程的学习。 | 解法同“210. 课程表 II”,使用队列实现拓扑排序。 |
| 210. 课程表 II medium |
总共有 n 门课需要选。给定一个数组,其中第i个元素[ai, bi]表示在选修课程 ai 前必须 先选修 bi。返回为了学完所有课程所安排的学习顺序。如果不可能完成所有课程,返回一个空数组。 | 拓扑排序(topological sort):有向无环图排序的算法。给定有向无环图中的$N$个节点,把它们排序成一个线性序列;若原图中节点 $i$ 指向节点 $j$,则排序结果中 $i$ 一定在 $j$ 之前。首先计算图中每一个节点的入度,并对入度为0的节点加入队列。然后只要队列非空,就进行以下操作:取出队列队首元素,同时将这个节点的每一个后续节点入度−1,若操作后的节点入度为0,则继续将该节点加入队列。 |
| 785. 判断二分图 medium |
存在一个无向图,判断该图是否为二分图。二分图定义:如果能将一个图的节点集合分割成两个独立的子集 A 和 B ,并使图中的每一条边的两个节点一个来自 A 集合,一个来自 B 集合,就将这个图称为二分图。 | 染色法:任选一个节点给它染成红色,随后将该节点直接相连的所有节点染成绿色;以此类推,直到无向图中的每个节点均被染色。如果染色过程中访问到一个已经染色的节点与将要给它染上的颜色不相同,则该无向图不是二分图。若无向图不一定保证连通,则需要进行多次遍历,直到每一个节点都被染色。 |
| 1462. 课程表 IV medium |
总共有 n 门课需要选。给定一个数组,其中第i个元素[ai, bi]表示在选修课程 ai 前必须 先选修 bi。给定一个数组,对于第 j 个查询,判断课程 uj 是否是课程 vj 的先决条件。 | 构造矩阵isPre[x][y]表示课程 x 是否是课程 y 的直接或间接先决条件。通过拓扑排序遍历课程,每次取出队列队首元素时,将这个节点及其所有前置条件节点设置为所有后续节点的前置条件节点。 |
| 1761. 一个图中连通三元组的最小度数 hard |
给定一个无向图,一个连通三元组指的是三个节点组成的集合且这三个点之间两两有边。连通三元组的度数是所有满足此条件的边的数目:一个顶点在这个三元组内,而另一个顶点不在这个三元组内。返回所有连通三元组中度数的最小值。 | 任意一个三元组$i,j,k$的度数计算为$degree[i]+degree[j]+degree[k]-6$;则可以遍历所有连通三元组计算最小度数。剪枝:对度数进行排序,则对每一个顶点$i$,其第一个构成的三元组是该顶点构成三元组中度数最小者。 |
| 2050. 并行课程 III hard |
总共有 n 门课需要选。给定一个数组,其中第i个元素[ai, bi]表示在选修课程 ai 前必须 先选修 bi;再给定一个整数数组,其中第i个元素表示完成第 i 门课程需要花费的月份数。可以同时上任意门课程,返回完成所有课程所需要的最少月份数。 | 使用拓扑排序获得课程的排序结果,对于每个入度为零的课程i,定义状态$dp[i]$为修完该课程需要的月份数,并构造状态转移方程$dp[i] = max_{j \in prev[i]} dp[j] + time[i]$,其中$prev[i]$是课程i的前置课程。 |
⚪ 其他数据结构
(1)前缀和与积分图
一维的前缀和(prefix sum),二维的积分图(integral image),都是把每个位置之前的一维线段或二维矩形预先存储,方便加速计算。
如果需要对前缀和或积分图的值做寻址,则要存在哈希表里;如果要对每个位置记录前缀和或积分图的值,则可以储存到一维或二维数组里,可以通过动态规划实现。
下面是构造一维前缀和的例子。需要注意前缀和索引$i$的含义是数组前$i$项的和,从前$0$个和到前$n$个和,则数组总的长度是$n+1$。
\[sums[i] = sums[i-1] + nums[i-1]\]# 写法①
sums = [0]
for num in nums:
sums.append(sums[-1] + num)
# 写法②
sums = list(accumulate(num))
下面是构造二维积分图的例子。
\[\begin{aligned} sums[i][j] = &sums[i-1][j] + sums[i][j-1] \\ & - sums[i-1][j-1] + nums[i-1][j-1] \end{aligned}\]sums = [[0]*(n+1) for _ in range(m+1)]
for i in range(1, m+1):
for j in range(1, n+1):
sums[i][j] = sums[i][j-1]+sums[i-1][j]-sums[i-1][j-1]+nums[i-1][j-1]

| 题目 | 题干 | 解法 |
|---|---|---|
| 238. 除自身以外数组的乘积 easy |
给定一个整数数组,返回一个新数组,其中第i个元素等于原数组中除该元素之外其余各元素的乘积。 | 把整数数组转化为前缀积与后缀积的形式。 |
| 303. 区域和检索 - 数组不可变 easy |
给定一个整数数组,计算索引left和right(包含left和right)之间的元素的和。 | 把整数数组转化为前缀和。 |
| 304. 二维区域和检索 - 矩阵不可变 medium |
给定一个二维矩阵,计算其子矩形范围内元素的总和。 | 把二维矩阵转化为积分图。 |
| 560. 和为 K 的子数组 medium |
给定一个整数数组和一个整数k,统计该数组中和为k的连续子数组的个数。 | 使用哈希表存储前缀和出现的次数。 |
| 1171. 从链表中删去总和值为零的连续节点 medium |
给定一个链表的头节点,反复删去链表中由总和值为0的连续节点组成的序列,直到不存在这样的序列为止。 | 若链表中出现前缀和相同的两个节点,则两个节点之间的序列总和为0。第一次遍历链表,使用哈希字典存储当前前缀和与当前节点,如果相同前缀和已经存在,直接覆盖掉原有节点;第二次遍历链表,如果存在与当前前缀和相同的后续节点,则跳过中间的节点。 |
| 1177. 构建回文串检测 medium |
给定一个小写字母字符串$s$,每次检测可以重新排列$s[l:r]$,并从中选择最多$k$项替换成任何小写字母。判断子串是否可以变成回文形式的字符串。 | 问题等价于统计子串中奇数数量字母的总数,回文串要求最多有(奇数长度:$1$;偶数长度:$0$)个奇数数量字母,且每一次替换能够减少$2$个奇数字母数。以前缀数组通过异或运算累计字母数量(奇数为$1$偶数为$0$)。 |
| 2559. 统计范围内的元音字符串数 medium |
给定一个字符串数组和一个二维整数数组,整数数组中的每个查询$(l_i,r_i)$会要求我们统计在字符串数组中下标在$l_i$到$r_i$范围内(包含这两个值)并且以元音开头和结尾的字符串的数目。返回一个整数数组,其中数组的第$i$个元素对应第$i$个查询的答案。 | 构造是否为元音开头和结尾(满足条件值为1,否则为0)的前缀和。 |
(2)并查集
并查集(union-find)是一种树型的数据结构,用于处理一些不相交集合(disjoint sets)的合并及查询问题。
假设存在 $n$ 个节点,我们先将所有节点的父亲标为自己;每次要连接节点 $i$ 和 $j$ 时,可以将 $i$ 的父亲标为 $j$;每次要查询两个节点是否相连时,可以查找 $i$ 和 $j$ 的祖先是否最终为同一个人。
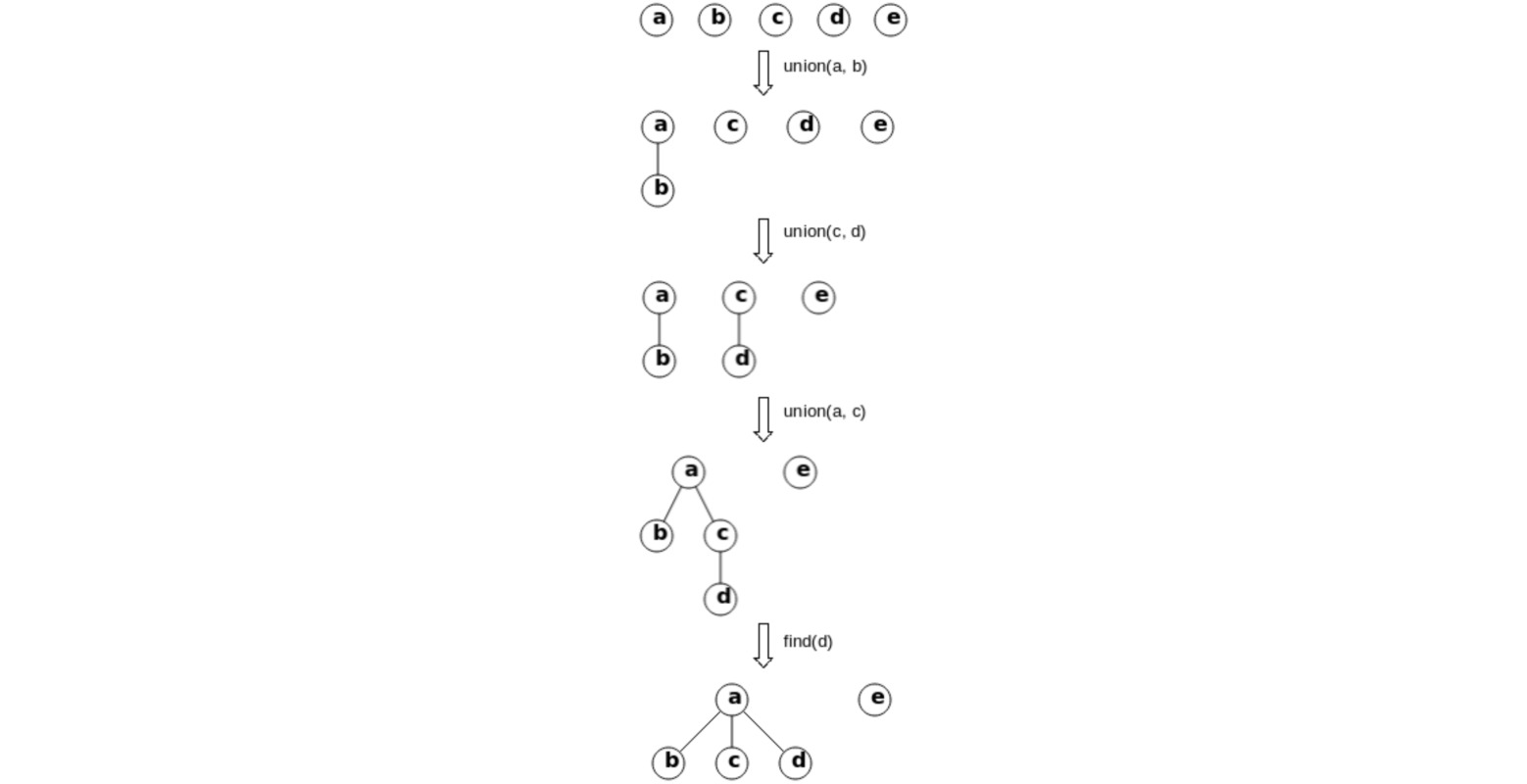
并查集维护一个数组parent,数组中维护的是元素的下标索引,这个下标索引指向该元素的父元素。并查集主要有三个功能:
- 寻找根节点:
find(u),也就是判断节点$u$的祖先节点是哪个节点; - 将两个节点接入到同一个集合:
union(u, v),将两个节点$u,v$连在同一个根节点上; - 判断两个节点是否在同一个集合:
same(u, v),就是判断两个节点是不是属于同一个根节点。
# 并查集初始化
parent = list(range(n))
# 并查集里寻根
def find(u):
return u if parent[u] == u else find(parent[u])
# 将 v->u 这条边加入并查集
def union(u, v):
u, v = find(u), find(v)
if u == v:
return
parent[v] = u
# 判断 u 和 v 是否属于同一个根
def same(u, v):
return find(u) == find(v) # 注意是find不是parent!!
为了加速查找,我们可以使用路径压缩和按秩合并来优化并查集:
- 按秩合并:秩定义为节点的最大深度。在执行
union(u, v)时,将秩大的根节点设置为合并后的根节点,避免了树的深度增加(避免后续的节点查询时间长)。 - 路径压缩:在执行
find(u)时,当在寻找一个节点的根节点root时,直接将该节点的所有长辈节点全部指向根节点root。后续寻找这些节点的根节点时可以节省很长一段搜索路径。
parent = list(range(n))
rank = [1]*n # 记录每个节点的秩
def find(u):
# 路径压缩
if u != parent[u]:
parent[u] = find(parent[u])
return parent[u]
def union(u, v):
u, v = find(u), find(v)
if u == v:
return
# 按秩合并
if rank[u] < rank[v]:
parent[u] = v
elif rank[u] > rank[v]:
parent[v] = u
else:
parent[v] = u
rank[u] += 1
并查集通常被用于判断节点的连通性问题。
| 题目 | 题干 | 解法 |
|---|---|---|
| 684. 冗余连接 medium |
给定往一棵 n 个节点 (节点值 1~n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间,且这条附加的边不属于树中已存在的边。找出一条可以删去的边,删除后可使得剩余部分是一个有着 n 个节点的树。 | 通过并查集寻找附加的边。遍历每一条边,边的两个节点如果不在同一个集合,就加入集合。如果边的两个节点出现在同一个集合里,说明两个节点已经连在一起了。 |
| 721. 账户合并 medium |
给定一个字符串列表,其中第一个元素是名称,其余元素表示该账户的邮箱地址。合并这些账户:如果两个账户都有一些共同的邮箱地址,则两个账户必定属于同一个人。 | 遍历每个账户下的邮箱,判断该邮箱是否在其他账户下出现。如果两个账户下出现了相同的邮箱,那么将两个账户的连通分量进行合并。最后遍历并查集中每个连通分量,将所有连通分量内部账户的邮箱全部合并。 |
| 839. 相似字符串组 hard |
如果两个字符串相等或其中一个字符串交换两个不同位置的字母后与另一个字符串相等,则称两个字符串相似。给定一个字符串列表,列表中的每个字符串都是其它所有字符串的一个字母异位词,求有多少个相似字符串组。 | 枚举给定序列中的任意一对字符串,检查其是否具有相似性,如果相似,那么就将这对字符串相连。 |
| 990. 等式方程的可满足性 medium |
给定一个由表示变量之间关系的字符串方程组成的数组,每个字符串方程采用两种不同的形式之一:”a==b” 或 “a!=b”。判断是否可以将整数分配给变量名,以便满足所有给定的方程。 | 首先遍历所有的等式,构造并查集。同一个等式中的两个变量属于同一个连通分量。然后遍历所有的不等式。同一个不等式中的两个变量不能属于同一个连通分量。 |
| 1061. 按字典序排列最小的等效字符串 medium |
给定长度相同的两组等价字符串,利用它们的等价信息,找出任意字符串的按字典序排列最小的等价字符串。 | 利用并查集维护任意字符的连通性,对于字符串中的每个字符,将其替换为连通的最小字符。 |
| 1202. 交换字符串中的元素 medium |
给定一个字符串,以及该字符串中的一些「索引对」数组,表示字符串中的两个索引。任意多次交换数组中任意一对索引处的字符。返回在经过若干次交换后可以变成的按字典序最小的字符串。 | 利用并查集维护任意两点的连通性,将同属一个连通块内的点提取出来,直接排序后放置回其在字符串中的原位置即可。 |
(3)设计数据结构
在设计复合类型的数据结构时,可以通过列表进行数据存储,从而加速连续选址或删除值;也可以通过哈希字典进行辅助记录或加速寻址。
| 题目 | 题干 | 解法 |
|---|---|---|
| 173. 二叉搜索树迭代器 medium |
实现一个二叉搜索树迭代器类,表示一个按中序遍历二叉搜索树的迭代器: | 使用中序遍历预先读取二叉树的每一个元素,最终存储为一个列表。 |
| 208. 实现 Trie (前缀树) medium |
前缀树是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。实现一个前缀树,包含功能:插入字符串,判断一个字符串或前缀是否存在。 | 建立哈希字典依次存储字符串中的字符,并标记字符串的结尾。 |
| 341. 扁平化嵌套列表迭代器 medium |
给定一个嵌套的整数列表。每个元素要么是一个整数,要么是一个列表;该列表的元素也可能是整数或者是其他列表。实现一个迭代器将其扁平化,使之能够遍历这个列表中的所有整数。 | 使用深度优先搜索依次读取嵌套的整数列表的每一个整数元素,最终存储为一个整数列表。 |
| 380. O(1) 时间插入、删除和获取随机元素 medium |
实现RandomizedSet类:以O(1)时间复杂度插入、移除元素,以及随机返回现有集合中的一项。 | 变长数组(可以在 O(1) 的时间内完成获取随机元素操作)中存储元素,哈希表(可以在 O(1) 的时间内完成插入和删除操作)中存储每个元素在变长数组中的下标。 |
| 432. 全 O(1) 的数据结构 hard |
设计一个用于存储字符串计数的数据结构,并能够返回计数最小和最大的字符串。 | 使用一个哈希字典存储“字符串:计数值”;使用一个TreeMap维护“计数值:字符串”。 |
| 707. 设计链表 medium |
使用单链表或者双链表,设计并实现自己的链表。 | 维护一个链表的长度变量,自定义链表节点构造链表。 |
| 1172. 餐盘栈 hard |
实现一个叫「餐盘」的类:把无限数量的栈排成一行,每个栈的的最大容量都相同。包含功能:将给出的正整数推入从左往右第一个没有满的栈;弹出从右往左第一个非空栈顶部的值;弹出给定编号的栈顶部的值。 | 使用数组模拟栈,使用有序列表维护未满栈和未空栈的编号。 |

