Support Vector Machine.

本文目录：

1. 线性支持向量机
2. 对偶支持向量机：降低算法复杂度
3. 核支持向量机：解决线性不可分(引入核方法)
4. 软间隔支持向量机：解决线性不可分(引入松弛变量)
5. 序列最小最优化(SMO)算法
6. 概率支持向量机
7. 最小二乘支持向量机

（注：为推导方便，若无特别说明以下讨论均在输出为$±1$的二分类任务上进行。）

1. 线性支持向量机

线性支持向量机(Linear SVM)也叫硬间隔支持向量机(Hard-margin SVM)。

(1)问题分析

假设数据集\(\{(x^{(1)},y^{(1)}),...,(x^{(N)},y^{(N)})\}\)是线性可分的，其中\(x \in \Bbb{R}^d\)，\(y \in \{-1,+1\}\)。

特征空间中的一个超平面可以表示为$w^Tx+b=0$，希望能找到一个分离超平面(separating hyperplane)对样本正确的分类：

这个条件记为：

$w$为超平面的法向量，决定超平面的方向；$b$是位移项，决定超平面与原点的距离。超平面仅仅区分样本是不够的，如果分离超平面距离某些样本点过近，当样本点受到噪声的扰动时，会使得分类结果出错，因此希望每一个样本点到该超平面得距离尽可能大：

定义超平面到所有样本点的距离为间隔(margin)，问题是找到间隔最大的超平面，下面解释如何求间隔。

(2)函数间隔与几何间隔

称上面定义的$y^{(i)}(w^Tx^{(i)}+b)$为样本点到超平面的函数间隔(functional margin)，可以定性地判断样本点到超平面的距离。

超平面$w^Tx+b=0$中的$w$是其法向量，证明如下：

任取超平面上两点$x’$、$x’’$，则满足$w^Tx’+b=0$、$w^Tx’‘+b=0$，两式做差得： $w^T(x’-x’’)=0$, 即向量$w$正交于超平面。

空间中任意一点$x$到该超平面\(w^Tx+b=0\)的距离$dis(x,w,b)$是该点到超平面上任意一点$x’$的连线(记连线与超平面法线的夹角为$\theta$)在法向量$w$方向上的投影：

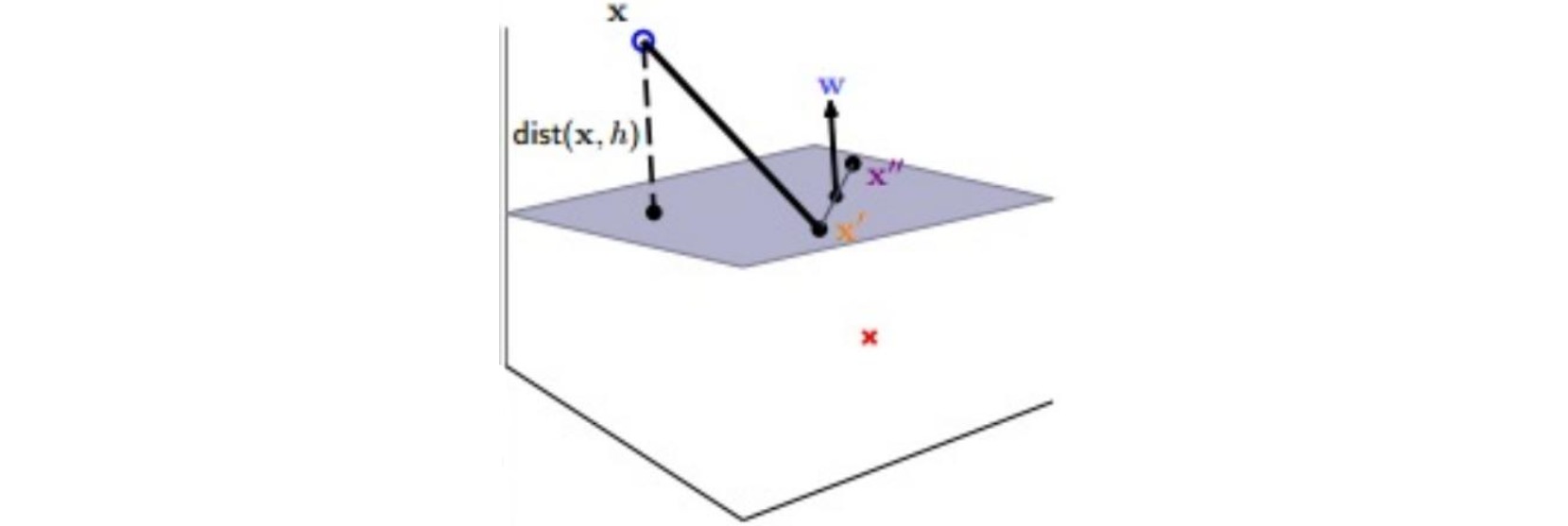
为了去掉绝对值运算，上式修改为：

定义超平面的几何间隔(geometric margin)为所有样本点到该超平面距离的最小值：

则线性支持向量机的问题列为：

(3)一些化简

注意到超平面$w^Tx+b=0$的系数$w$和$b$的数值可以放缩，不会影响该超平面(超平面仅由$w$和$b$的比值决定)，为简化计算，可通过选取合适的$w$和$b$使得样本点到该超平面的最新函数间隔为$1$：

则原约束可以修改为：

超平面的几何间隔为：

目标函数变为：

将目标函数转换为：

则线性支持向量机的问题转化为：

观察这个最优化问题，特点：

1. 目标函数是二次函数
2. 约束条件是变量的一次函数

该问题是一个凸二次规划(convex quadratic programming)问题，可以直接使用对应的工具包求解：

由该方法得到的超平面称为这些样本点的最大间隔分离超平面(large-margin separating hyperplane)，若样本集线性可分，则该超平面是存在且唯一。

(4)支持向量

线性支持向量机问题求解后，会有一些点$(x^{(i)},y^{(i)})$满足$y^{(i)}(w^Tx^{(i)}+b) = 1$，其余点$(x^{(j)},y^{(j)})$满足$y^{(j)}(w^Tx^{(j)}+b) > 1$,

采用反证法证明上述结论，即假设所有点均满足$y^{(i)}(w^Tx^{(i)}+b) > 1$，此时的$w$应满足$\mathop{\min} \frac{1}{2}w^Tw$， 对$w$和$b$同时缩小一点，仍然满足不等式，但打破了最小目标函数的条件，故假设不成立。

称满足$y^{(i)}(w^Tx^{(i)}+b) = 1$的样本点$(x^{(i)},y^{(i)})$为支持向量(support vector)，最大间隔分离超平面由这些支持向量唯一确定。

可以计算得到超平面的最大间隔为\(\frac{2}{\| w \|}\)。

2. 对偶支持向量机

在支持向量机问题中，数据集\(\{(x^{(1)},y^{(1)}),...,(x^{(N)},y^{(N)})\},x \in \Bbb{R}^d\)，即共有$N$个样本，其中每个样本的特征是$d$维的；

上一节得到的二次规划问题称为支持向量机的原问题(prime problem)，该优化问题有$d+1$个待求解的变量，有$N$个约束条件。

有时样本的特征维度远高于样本个数，即$d»N$，使得原问题求解较为复杂；当引入核方法之后，样本的特征维度将变成无限维，导致原问题是不可解的。因此引入对偶支持向量机(dual SVM)。

(1)拉格朗日函数

原二次规划问题是一个求解参数$w,b$的约束(constrained)问题，通过引入拉格朗日乘子 (Lagrange Multiplier) $\alpha$将其转化成对参数$w,b$的无约束(unconstrained)问题。

记拉格朗日函数(Lagrange function)：

则将原问题转化为：

这个优化问题没有显式地给出对参数$w,b$的约束，但仍与原问题等价，分析如下：

• 对于满足原约束条件$y^{(i)}(w^Tx^{(i)}+b) ≥ 1$的$w,b$，为使拉格朗日函数最大需$α_i=0$，此时目标函数退化为$\frac{1}{2}w^Tw$;
• 对于使$y^{(i)}(w^Tx^{(i)}+b) < 1$的$w,b$，$α_i$可取$∞$，此时目标函数为$∞$；
• 最终的优化问题从上述两种情况中取较小者，即第一种情况，恰好就是原二次规划的问题。

(2)拉格朗日对偶问题

由不等式：

上式左端恒大于等于右端，自然大于等于右端给定$α$的情况：

上式左端是引入拉格朗日函数的原问题，右端是其拉格朗日对偶问题(Lagrange dual problem)，具有弱对偶关系(weak duality)。

当优化问题是二次规划时，上式具有强对偶关系(strong duality)，即：

最终得到对偶支持向量机的优化问题：

(3)求解对偶问题

对偶问题是$w,b$的无约束问题，令其偏导数为零：

解得：

对拉格朗日函数进行化简：

对偶问题转化为只与$α$有关的形式：

该优化问题有$N$个待求解的变量，有$N+1$个约束条件。

这是一个二次规划问题，可以使用第$5$节介绍的序列最小最优化算法求解；也可以直接使用对应的工具包求解，注意其中的等式约束可以拆解成两个不等式约束：

(4)KKT条件

求解得到$α$后，可以用KKT条件得到$w,b$。

KKT条件(Karush-Kuhn-Tucker condition)是强对偶关系的等价条件，可用于求解优化问题；

对于对偶支持向量机问题，KKT条件包括：

• 原问题的约束条件：$y^{(i)}(w^Tx^{(i)}+b) ≥ 1, \quad i=1,2,…,N$
• 对偶问题的约束条件：$α_i≥0, \quad i=1,2,…,N$
• 拉格朗日函数的一阶导数为零：

• 互补松弛条件(complementary slackness)：

当得到$α$后，可直接得到$w$:

由互补松弛条件，任取一个$α_s≠0$，则$1-y^{(s)}(w^Tx^{(s)}+b) = 0$，解得：

称$α_i≠0$对应的样本点为支持向量(support vector)，支持向量机的模型参数仅由这些支持向量确定(若$α_i=0$则不会出现在$w$的计算中)。

则支持向量机的判别函数为：

3. 核支持向量机

对偶支持向量机把优化问题转化成$N$个待求解的变量、$N+1$个约束条件的问题，与样本的特征维度$d$无关。但是在求解问题时，需计算内积${(x^{(i)})}^Tx^{(j)}$，仍需要$O(d)$的运算复杂度。

与此同时，线性支持向量机要求数据集是线性可分的，根据核方法，对于线性不可分的数据集，通常引入一个特征变换$z = φ(x)$把原始输入空间映射为一个更高维度的特征空间，使得样本在这个特征空间内线性可分(如果原始空间为有限维，一定存在一个高维线性空间使得样本可分)，此时的问题变为：

问题的解：

则支持向量机的判别函数为：

当特征空间维度较高时(甚至是无穷维)，求解特征变换$φ(x)$以及特征变换的内积$φ(x)^Tφ(x’)$运算困难。因此引入核技巧(kernel trick)(参考核方法)。即在求解支持向量机问题中，不显式地计算特征变换$φ(x)$以及特征变换的内积$φ(x)^Tφ(x’)$，而是把计算特征变换$φ(x)$以及特征变换的内积$φ(x)^Tφ(x’)$转化为计算一个函数的值，这个函数称为核函数(kernel function)：

则核支持向量机(kernelized SVM)问题：

求解后可得最终的判别函数为：

4. 软间隔支持向量机

之前介绍的都是硬间隔(hard margin)支持向量机，在输入空间或特征空间中寻找一个最大间隔超平面。

对于线性不可分的数据，也可以适当放松条件，允许一些样本点不满足间隔条件甚至被错误分类，这种方法称为软间隔(soft margin)支持向量机。

定义松弛变量(slack variable,容忍度)对每个样本点到分离超平面的最小距离放松$ξ_i$，并使这些放松条件尽可能小：

超参数惩罚系数$C$权衡间隔大小和分类错误点的容忍程度。

• $C$越大，样本点到超平面的距离越大，分类错误的点数减少，最大间隔减小；
• $C$越小，样本点到超平面的距离限制减小，最大间隔增大，但可能分类错误的点数增加。

(1)对偶问题

软间隔支持向量机的优化问题也是二次规划问题，引入拉格朗日函数：

则对偶问题可写作：

令$\frac{\partial L(w,b,ξ,α,β)}{\partial ξ_i} = 0$，得：

把$β_i = C - α_i$代入对偶问题并化简得：

化简该对偶问题：

该优化问题有$N$个待求解的变量，有$2N+1$个约束条件；与硬间隔支持向量机问题相比，仅仅是多了对$α$的上界条件。

通过二次规划方法或SMO算法（见第$5$章）解得$α_i$后，利用KKT条件求解$w$和$b$：

由互补松弛条件：

• $α_i(1-ξ_i-y^{(i)}(w^Tx^{(i)}+b))=0$
• $-β_iξ_i = (C - α_i)ξ_i = 0$

任选一个满足$0<α_s<C$的支持向量$α_s$，使得：

(2)几何解释

根据$α_i$的取值不同，样本点可分为三类：

• $α_i=0$：此时$ξ_i = 0$，对应最大间隔超平面完全分类正确的样本点；
• $0<α_i<C$：此时$ξ_i = 0$，$y^{(i)}(w^Tx^{(i)}+b)=1$，对应恰好在间隔边界上的点，称为free support vector，对应图中正方形框的点；
• $α_i=C$：此时$ξ_i ≠ 0$，$y^{(i)}(w^Tx^{(i)}+b)=1-ξ_i$，对应放松了间隔条件的点，称为bounded support vector，对应图中三角形框的点，此时若$ξ_i < 1$则样本点分类正确，$ξ_i > 1$则样本点分类错误。

(3)超参数C的选择

通常用验证集选择超参数$C$。

对于$N$个样本采用留一交叉验证(leave-one-out cross validation)，其验证集误差满足以下不等式：

此时验证误差不超过样本集中支持向量所占的比例，证明如下：

• 若其中某个样本点是支持向量，将其划分出来作为验证集时，会使最终超平面改变，此时该点可能被错误分类，故误差$≤1$；
• 若其中某个样本点不是支持向量，将其划分出来作为验证集时，对最终超平面没有影响，此时该点仍会被分类正确，故误差$=0$。

故支持向量的个数一定程度上可以作为超参数选择的依据：

(4)合页损失(Hinge Loss)函数

软间隔支持向量机的优化问题：

分析约束条件，$ξ_i$描述的是样本点$(x^{(i)},y^{(i)})$到分离间隔$y(w^Tx+b)=1$的距离：

将上式表达为：

则软间隔支持向量机的优化问题等价于目标函数为合页损失函数(hinge loss)的优化问题：

其中正则化系数$λ=\frac{1}{2C}$。

由此可以看出，支持向量机的出发点“间隔最大化”具有一定的$L2$正则化的作用。

对于软间隔支持向量机，之所以采用对偶方法求解约束规划而不是求解hinge loss，主要原因如下：

1. 凸二次规划问题具有良好的解析性质，可以求得解析解；而上述无约束目标函数需要用梯度下降方法，且存在求最大值的操作，不利于微分；
2. 直接解上面的无约束目标函数无法直接使用核方法。

当标签为$±1$时，比较感知机、逻辑回归和支持向量机的损失函数：

• 感知机：0/1损失：\(E_{0/1}=[\text{sign}(wx)=y]=[\text{sign}(ywx)=1]\)
• 逻辑回归：以$2$为底的交叉熵：\(E_{\text{scaled-ce}}=\text{log}_2(1+\text{exp}(-ywx))=\frac{1}{ln2}E_{\text{ce}}\)
• 支持向量机：Hinge Loss：\(E_{\text{svm}}=[1-ywx]_+\)

经过换底后的交叉熵损失和支持向量机损失都是$0/1$损失的上界：

5. 序列最小最优化算法

序列最小最优化(sequential minimal optimization，SMO)算法是用来解支持向量机对偶问题的数值方法。

引入核函数的软间隔支持向量机的优化问题如下：

该优化问题需要求解$N$个参数$α_1,…,α_N$。

序列最小最优化算法的思想是，在循环中每次选择其中的两个参数$α_1,α_2$，固定其他参数进行优化(不能只选择一个参数$\alpha_1$优化，因为这样会由约束$\sum_{i=1}^{N} {α_iy^{(i)}} = 0$直接导出$\alpha_1$)，固定其余参数，用解析的方法解两个变量的二次规划问题。

注意到子问题中只有一个变量是自由变量，另外一个变量可以被表示为：

(1)两个变量的二次规划问题

当选择$α_1,α_2$作为变量时，子问题为：

其中记$K_{ij}=K(x^{(i)},x^{(j)})$。

记$g(x)$为当前时刻支持向量机的判别函数，

记当前时刻与真实标签的差值为$E(x^{(i)}) = g(x^{(i)})-y^{(i)}$；

若先求解变量$α_2$，将等式约束$α_1 = y^{(1)}(α_2y^{(2)}-\sum_{i=3}^{N} {α_iy^{(i)}})$代入目标函数后，对其求关于$α_2$的偏导数，令其为零，得：

考虑不等式约束$0≤α_1≤C,0≤α_2≤C$，需要限制$α_2^{new}$的更新范围：

当$y^{(1)} ≠ y^{(2)}$时:

当$y^{(1)} = y^{(2)}$时:

因此更新后的$α_2^{new}$：

由约束条件$y^{(1)}α_1^{old} + y^{(2)}α_2^{old} = y^{(1)}α_1^{new} + y^{(2)}α_2^{new}$得：

算法每一步迭代得到新的$α_1,α_2$后需要更新参数$b$:

若$0<α_1^{new}<C$，则：

若$0<α_2^{new}<C$，则：

取$b^{new}=\frac{b_1^{new}+b_2^{new}}{2}$。

(2)变量的选择

每次循环更新当前时刻与真实标签的差值：

• 外层循环选择第一个变量：选择误差$\mid E(x^{(i)}) \mid$最大的样本对应的$α_i$(违反KKT条件程度最大的变量)；
• 内层循环选择第二个变量：选择使$\mid E(x^{(i)})-E(x^{(j)}) \mid$最大的样本对应的$α_j$(选择使目标函数数值增长最快的变量，启发式地选择两变量使得所对应样本之间的间隔最大)。

6. 概率支持向量机

概率支持向量机(probabilistic SVM)是将支持向量机和逻辑回归结合起来的方法。既具有支持向量机问题解析的优良性，又具有逻辑回归中样本概率极大似然的思想。

该方法先求解核函数支持向量机问题，得到（未经过符号函数）的模型输出：

将该标量通过scaling参数$A$和shifting参数$B$后，喂入Logistic函数，得到预测概率：

该问题只有两个变量$A$和$B$。

概率支持向量机的熵损失函数（标签为$±1$）：

这是一个无约束的凸优化问题，可以使用梯度下降方法。

7. 最小二乘支持向量机

最小二乘支持向量机(least-squares SVM，LSSVM)就是将kernel ridge regression用于分类任务。

由引入核方法的岭回归对数据拟合，得到回归方程：

用该方程作为分类超平面，就得到最小二乘支持向量机模型。其中超平面是由回归的均方误差确定的，故称为“最小二乘”。

比较软间隔支持向量机和最小二乘支持向量机：

两者的分类边界是类似的，但前者的支持向量少（对应$α≠0$的样本），后者的支持向量多（对应$β≠0$的样本），计算量更大。