Logistic Regression.
本文目录:
- 逻辑回归模型
- Logistic函数
- 交叉熵损失
- 梯度下降法
- 核逻辑回归
1. 逻辑回归模型
逻辑回归(logistic regression)是一种二分类模型,其思想是通过引入一个函数将线性回归的输出限制在$[0,1]$之间。最理想的函数是单位阶跃(unit-step)函数(也称Heaviside函数),但是该函数不连续,因此选用Logistic函数$σ(\cdot)$近似替代。
若记每一个样本点$x = (1,x_1,x_2,…,x_d)^T \in \Bbb{R}^{d+1}$,模型权重参数$w = (w_0,w_1,w_2,…,w_d)^T \in \Bbb{R}^{d+1}$,则逻辑回归模型:
\[\hat{y} = σ(\sum_{j=0}^{d} {w_jx_j}) = σ(w^Tx)\]2. Logistic函数
Logistic函数又叫Sigmoid函数,其表达式、一阶导数和函数曲线如下:
\[\begin{aligned} σ(x)&= \frac{1}{1+e^{-x}} \\ σ'(x)&= σ(x)(1-σ(x)) \end{aligned}\]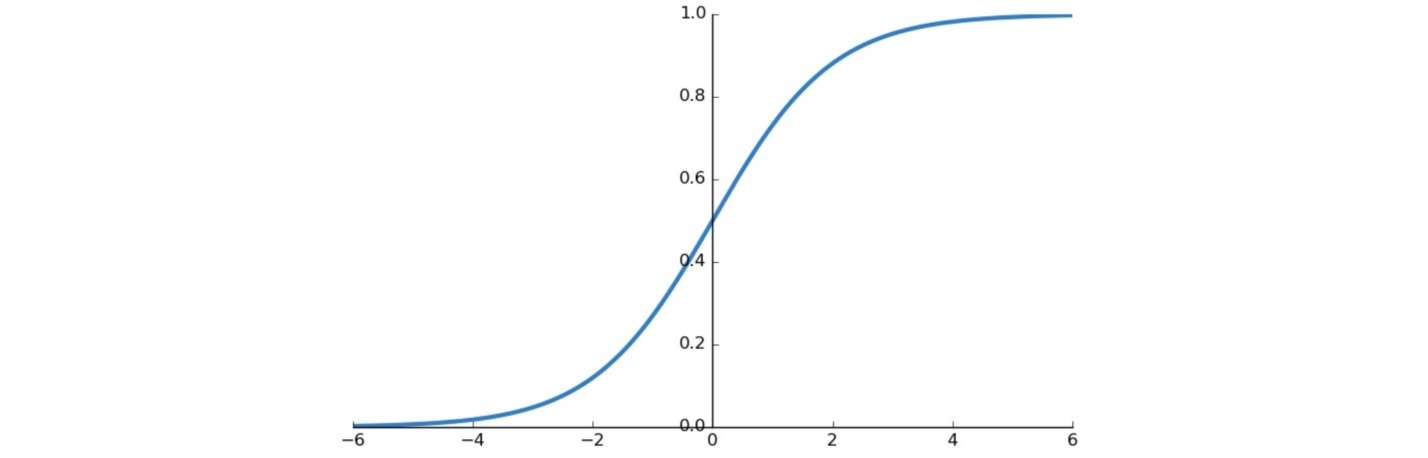
注意到引入Logistic函数后逻辑回归模型:
\[\hat{y} = σ(w^Tx) = \frac{1}{1+e^{-w^Tx}}\]输出$y=\frac{1}{1+e^{-w^Tx}}$表示类别为$1$的概率,$1-y=\frac{e^{-w^Tx}}{1+e^{-w^Tx}}$表示类别为$0$的概率。
$\frac{y}{1-y}$称为几率(odds),表明$输入x$的类别为$1$的相对可能性,对数几率(log odds, logit)可表示为:
\[\ln(\frac{y}{1-y}) = w^Tx\]上式表明逻辑回归是一种广义线性模型,实际上是在用线性回归模型的预测结果去逼近真实标签的对数几率,因此逻辑回归也称作对数几率回归。
3. 交叉熵损失
逻辑回归的损失函数为交叉熵损失(cross-entropy loss),可以由极大似然估计推导。
(1) 标签为0和1
把分类标签设置为\(y \in \{0,+1\}\)。
Logistic函数把输入压缩到$0$到$1$之间,可以看作对$y$预测的概率:
\[\begin{aligned} P(y=1 | x) &= σ(w^Tx) \\ P(y=0 | x) &= 1-σ(w^Tx) \end{aligned}\]上式表示预测结果服从Bernoulli分布,可以表达为:
\[P(y | x) = {σ(w^Tx)}^{y}{(1-σ(w^Tx))}^{1-y}\]若样本集\(X=\{x^{(1)},...,x^{(N)}\}\),标签集\(y=\{y^{(1)},...,y^{(N)}\}\),列出对数似然方程:
\[\begin{aligned}& \ln( \prod_{i=1}^{N} { {σ(w^T x^{(i)})}^{y^{(i)}} {(1-σ(w^T x^{(i)}))}^{1-y^{(i)}} } ) \\&= \sum_{i=1}^{N} { \ln( {σ(w^Tx^{(i)})}^{y^{(i)}} {(1-σ(w^Tx^{(i)}))}^{1-y^{(i)}} ) } \\& = \sum_{i=1}^{N} { y^{(i)} \ln(σ(w^Tx^{(i)})) + (1-y^{(i)}) \ln(1-σ(w^Tx^{(i)})) } \end{aligned}\]极大化似然概率等价于极小化以下损失函数:
\[L(w) = \sum_{i=1}^{N} {-y^{(i)}\ln(σ(w^Tx^{(i)})) - (1-y^{(i)})\ln(1-σ(w^Tx^{(i)}))}\]上式为具有熵的形式($-p\log p$),因此称为交叉熵损失(cross-entropy loss)。
若希望损失函数为零,则需:
\[\begin{cases} w^Tx → +∞, & y=1 \\ w^Tx → -∞, & y=0 \end{cases}\]此时要求数据集是线性可分的。
(2) 标签为±1
也可以把分类标签设置为\(y \in \{-1,+1\}\),从而与感知机、支持向量机等模型的书写方式相同。
由Logistic函数的性质:$1-σ(x)=σ(-x)$;输出概率为:
\[\begin{aligned} P(y=1 | x) &= σ(w^Tx) \\ P(y=-1 | x) &= 1-σ(w^Tx) = σ(-w^Tx) \end{aligned}\]或者统一写为:
\[P(y | x) = σ(yw^Tx)\]若样本集\(X=\{x^{(1)},...,x^{(N)}\}\),标签集\(y=\{y^{(1)},...,y^{(N)}\}\),列出对数似然方程:
\[\ln(\prod_{i=1}^{N} {σ(y^{(i)}w^Tx^{(i)})} = \sum_{i=1}^{N} {\ln(σ(y^{(i)}w^Tx^{(i)}))}\]似然概率极大化,等价于以下损失函数极小化:
\[\begin{aligned} L(w) &= \sum_{i=1}^{N} {-\ln(σ(y^{(i)}w^Tx^{(i)}))} \\&= \sum_{i=1}^{N} {\ln(1+\exp(-y^{(i)}w^Tx^{(i)}))} \end{aligned}\]上式也为交叉熵损失(cross-entropy loss)。
(3) 损失函数的比较
当标签为$±1$时,比较感知机、线性回归和逻辑回归的损失函数:
- 感知机:0/1损失:\(E_{0/1}=[\text{sign}(wx)=y]=[\text{sign}(ywx)=1]\)
- 线性回归:均方误差:\(E_{sqr}=(wx-y)^2=(ywx-1)^2\)
- 逻辑回归:交叉熵:\(E_{ce}=\ln(1+\exp(-ywx))\)
- 以$2$为底的交叉熵:\(E_{scaled-ce}=\log_2(1+\exp(-ywx))=\frac{1}{ln2}E_{ce}\)
经过换底后的交叉熵损失和平方损失都是$0/1$损失的上界:

比较可得,$0/1$损失整体更小,但优化困难(NP-hard);均方误差和交叉熵更大,但可以把问题转化成凸优化问题(存在解析解或梯度下降求解)。
4. 梯度下降法
逻辑回归的损失函数(交叉熵损失)无解析解,是一个无约束的优化问题,可以用梯度下降法求解。
以标签为$0$和$1$的交叉熵损失为例:
\[L(w) = \sum_{i=1}^{N} {-y^{(i)}\ln(σ(w^Tx^{(i)})) - (1-y^{(i)})\ln(1-σ(w^Tx^{(i)}))}\]求损失$L(w)$的梯度:
\[\begin{aligned} \nabla_w L(w) &= \nabla_w\sum_{i=1}^{N} {-y^{(i)}\ln(σ(w^Tx^{(i)})) - (1-y^{(i)})\ln(1-σ(w^Tx^{(i)}))} \\ &= \sum_{i=1}^{N} {-y^{(i)}\nabla_w\ln(σ(w^Tx^{(i)})) - (1-y^{(i)})\nabla_w\ln(1-σ(w^Tx^{(i)}))}\\ &= \sum_{i=1}^{N} {-y^{(i)}(1-σ(w^Tx^{(i)}))x^{(i)} + (1-y^{(i)})σ(w^Tx^{(i)})x^{(i)}} \\ &= \sum_{i=1}^{N} {-y^{(i)}(1-σ(w^Tx^{(i)}))x^{(i)} + (1-y^{(i)})σ(w^Tx^{(i)})x^{(i)}}\\ &= \sum_{i=1}^{N} {-(y^{(i)}-σ(w^Tx^{(i)}))x^{(i)}}\\ &= -X^{T}(Y-σ(w^TX)) \end{aligned}\]因此参数$w$的更新过程为:
\[w^{(t+1)} \leftarrow w^{(t)} +\eta X^{T}(Y-σ(w^TX))\]5. 核逻辑回归
将核方法引入逻辑回归,可以得到核逻辑回归(kernelized logistic regression),从而把线性模型转换成非线性模型。
使用$L2$正则化的逻辑回归的损失函数(标签为$0$和$1$)如下:
\[L(w) = \sum_{i=1}^{N} {-y^{(i)}\ln(σ(w^Tx^{(i)})) - (1-y^{(i)})\ln(1-σ(w^Tx^{(i)}))} + \frac{λ}{N}w^Tw\]由表示定理,权重最优解可以表示为:
\[w^* = \sum_{n=1}^{N} {β_nx^{(n)}}\]代入损失函数为:
\[L(β) = \sum_{i=1}^{N} {-y^{(i)}\ln(σ(\sum_{n=1}^{N} {β_n{x^{(n)}}^Tx^{(i)}})) - (1-y^{(i)})\ln(1-σ(\sum_{n=1}^{N} {β_n{x^{(n)}}^Tx^{(i)}}))} \\ + \frac{λ}{N}\sum_{i=1}^{N} {\sum_{j=1}^{N} {β_iβ_j{x^{(i)}}^Tx^{(j)}}}\]引入核函数\(K(x,x')={φ(x)}^Tφ(x')\)来代替样本的特征转换和内积运算,则核逻辑回归的损失函数为:
\[L(β) = \sum_{i=1}^{N} {-y^{(i)}\ln(σ(\sum_{n=1}^{N} {β_nK(x^{(n)},x^{(i)})})) - (1-y^{(i)})\ln(1-σ(\sum_{n=1}^{N} {β_nK(x^{(n)},x^{(i)})}))} \\ + \frac{λ}{N}\sum_{i=1}^{N} {\sum_{j=1}^{N} {β_iβ_jK(x^{(i)},x^{(j)})}}\]这是一个无约束的优化问题,可以用梯度下降法求解。


