Graph Neural Networks.

图神经网络 (Graph Neural Network, GNN)是用于处理图结构的神经网络，其核心思想是学习一个函数映射$f(\cdot)$，图中的节点$v_i$通过该映射可以聚合它自己的特征$x_i$与它的邻居特征$x_{j \in N(v_i)}$来生成节点$v_i$的新表示。

GNN可以分为两大类，基于空间（spatial-based）和基于谱（spectral-based）。

基于空间的GNN直接根据邻域聚合特征信息，把图粗化为高级子结构，可用于提取图的各级表示和执行下游任务。如NN4G, DCNN, DGC, MoNET, GraphSAGE, GAT, GIN。
基于谱的GNN把图网络通过傅里叶变换转换到谱域，引入滤波器处理图谱后通过逆变换还原到顶点域。如ChebNet, GCN, DropEdge。

本文目录：

Spatial-based GNN
Spectral-based GNN
Benchmarks

1. Spatial-based GNN

术语Terminology：

Aggregate: 用邻域的特征更新节点的隐状态
Readout: 把所有节点的特征集合起来代表整个图

方法:

NN4G (Neural Networks for Graph)
DCNN (Diffusion-Convolution Neural Network)
DGC (Diffusion Graph Convolution)
MoNET (Mixture Model Networks)
GraphSAGE
GAT (Graph Attention Networks)
GIN (Graph Isomorphism Network)

(1) NN4G (Neural Networks for Graph)

先对输入图的每个节点进行嵌入，得到初始隐状态：

（以节点$v3$为例）：$h_3^0 = \overline{w}_0x_3$

状态更新时，每个节点使用邻节点的状态和该节点的输入更新：

$Readout$时对每一层的隐状态的均值进行加权求和，得到输出：

(2) DCNN (Diffusion-Convolution Neural Network)

DCNN对第$l$个隐藏层的节点$v_l$，使用自身以及距离为$l+1$的节点状态进行更新。

如下图，在更新$h_3^1$时，使用$h_3^0$和距离为2的$h_1^0$进行更新：

$Readout$时把所有层的状态连接起来进行线性变换：

(3) DGC (Diffusion Graph Convolution)

DGC与DCNN的不同在于$Readout$时把所有层的状态相加：

(4) MoNET (Mixture Model Networks)

定义两节点$x$、$y$之间的“距离”$u$：

\[u(x,y) = (\frac{1}{\sqrt{deg(x)}},\frac{1}{\sqrt{deg(y)}})^T\]

其中$deg(x)$表示$x$的维度。

节点更新时采用对邻域节点加权求和的方法：

\[h_3^1 = w(\hat{u}_{3,0})×h_0^0 + w(\hat{u}_{3,2})×h_2^0 + w(\hat{u}_{3,4})×h_4^0\]

其中$w$是一个神经网络，$\hat{u}$是$u$的变换。

(5) GraphSAGE

GraphSAGE采用两个操作：Sample和aggregate。对于某节点，从其$k$邻域中采样节点，并根据采样的节点更新图信息。

(6) GAT (Graph Attention Networks)

用一个函数$f$实现注意力机制，用邻域节点的注意力分布加权更新参数：

(7) GIN (Graph Isomorphism Network)

节点的状态更新：

\[h_v^{(k)} = MLP^{(k)}((1+ε^{(k)})·h_v^{(k-1)} + \sum_{u \in \Bbb{N}(v)}^{} {h_u^{(k-1)}})\]

使用$MLP$代替了单层网络，$ε$是可学习参数，$\Bbb{N}$是邻节点集合。

该论文指出节点的状态更新应该用求和sum而不是均值mean或最大值max，因为均值或最大值可能会失效：

2. Spectral-based GNN

Spectral-based的思想是将图网络和卷积核通过傅里叶变换到谱域(spectral domain)，相乘后把结果通过傅里叶逆变换到顶点域(vertex domain)。

⚪ 谱图理论 Spectral Graph Theory

术语Terminology：

Graph:$G=(V,E)$,$N= \mid V \mid$，本文讨论无向图undirected graph。
Adjacency matrix(weight matrix):$A \in \Bbb{R}^{N×N}$表示节点间是否有连接，是对称矩阵。
Degree matrix:$D \in \Bbb{R}^{N×N}$表示节点的邻节点数量，是对角矩阵。
Signal on graph(vertices):$f:V → \Bbb{R}$,$f(i)$表示每个节点$i$的信号。
Graph Laplacian:$L=D-A$是对称的半正定矩阵。

谱分解Spectral Decomposition：$L=U \Lambda U^T$

对角矩阵$\Lambda = diag(λ_0,...,λ_{N-1}) \in \Bbb{R}^{N×N}$，$λ_i$表示频率frequency。
正交矩阵$U = [u_0,...,u_{N-1}] \in \Bbb{R}^{N×N}$，$u_i$表示基basis。

上述概念的例题：

$u_i$表示各节点中频率$λ_i$所占的权重；频率越大，相邻两节点之间的信号变化量越大：

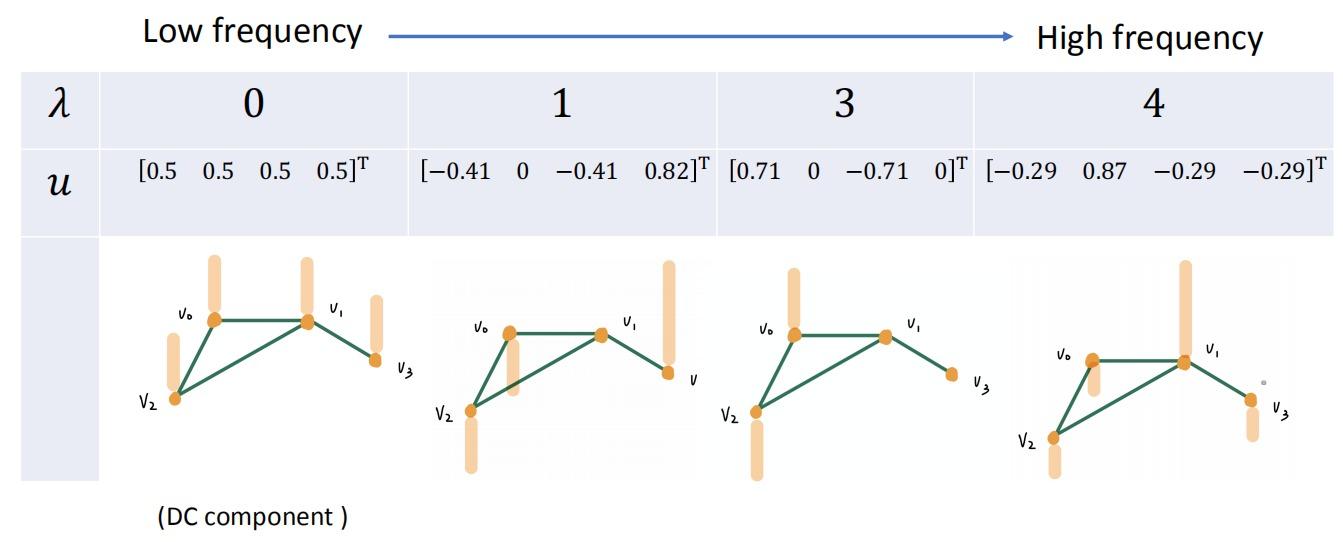
信号$x$的Graph Fourier Transform (GFT)：$\hat{x} = U^Tx$

信号$\hat{x}$的Inverse Graph Fourier Transform (IGFT)：$x = U\hat{x}$

⚪ 基于谱的GNN

将信号$x$通过$GFT$转换到$spectral$ $domain$：$\hat{x} = U^Tx$;
在$spectral$ $domain$设计滤波器$g_θ(\Lambda)$;
$vertex$ $domain$的卷积相当于$spectral$ $domain$的乘积：$\hat{y}=g_θ(\Lambda)\hat{x}$;
将信号$\hat{y}$通过$IGFT$转换到$vertex$ $domain$：$y = U\hat{y}$

计算：

\[y = U\hat{y} = Ug_θ(\Lambda)\hat{x} = Ug_θ(\Lambda)U^Tx = g_θ(U\Lambda U^T)x = g_θ(L)x\]

$g_θ(L)$可以是任何函数：

$g_θ(L)=log(I+L)=L-\frac{L^2}{2}+\frac{L^3}{3}...$
- 问题：学习复杂度$O(N)$
$g_θ(L)=cos(L)=I-\frac{L^2}{2!}+\frac{L^4}{4!}...$
- 问题：失去局部性

引理Lemma：如果一个图具有$N$个节点，则$L^N$不存在$0$元素，即使所有节点共享。

方法:

ChebNet
GCN(Graph Convolution Network)
DropEdge

(1) ChebNet

$g_θ(L)$使用$k$阶多项式函数函数：$g_θ(L) = \sum_{k=0}^{K} {θ_kL^k}$

由引理知上式是K-localized的，上式时间复杂度$O(N^2)$。

引入Chebyshev polynomial：

为使$λ \in [-1,1]$，做变换：$\overline{\Lambda}=\frac{2\Lambda}{λ_{max}}-I$

则$T_0(\overline{\Lambda})=I, \quad T_1(\overline{\Lambda})=\overline{\Lambda}, \quad T_k(\overline{\Lambda})=2\overline{\Lambda}T_{k-1}(\overline{\Lambda})-T_{k-2}(\overline{\Lambda})$

\[g_θ(\hat{L}) = \sum_{k=0}^{K} {θ'_kT_k(\hat{L})}\] \[y = g_θ(\hat{L})x = \sum_{k=0}^{K} {θ'_kT_k(\hat{L})}x\]

若记$\hat{x}_k = T_k(\hat{L})x$,则：

\[y = \sum_{k=0}^{K} {θ'_k\hat{x}_k} = [\hat{x}_0;...;\hat{x}_K][θ'_0;...;θ'_K]\]

上式时间复杂度$O(KE)$。

实际使用中，可以使用多个$g_θ$：