自注意力层的模仿初始化.
尽管Transformer在大规模预训练任务中表现出色,但它们很难在小规模数据集上进行训练。本文提出了一种针对Transformer模型的模仿初始化技术,通过模拟在预训练模型权重中观察到的结构和模式来初始化Transformer。
记自注意力层中的查询矩阵、键矩阵与值矩阵分别为$W_Q,W_K \in R^{d \times k},W_V \in R^{d \times d}$,多头映射矩阵为$W_{proj} \in R^{d \times d}$。其中注意力分布计算为:
\[A = softmax(\frac{1}{\sqrt{k}}XW_QW_K^TX^T) \in R^{n \times n}\]当采用多头自注意力时,每个头的输出为:
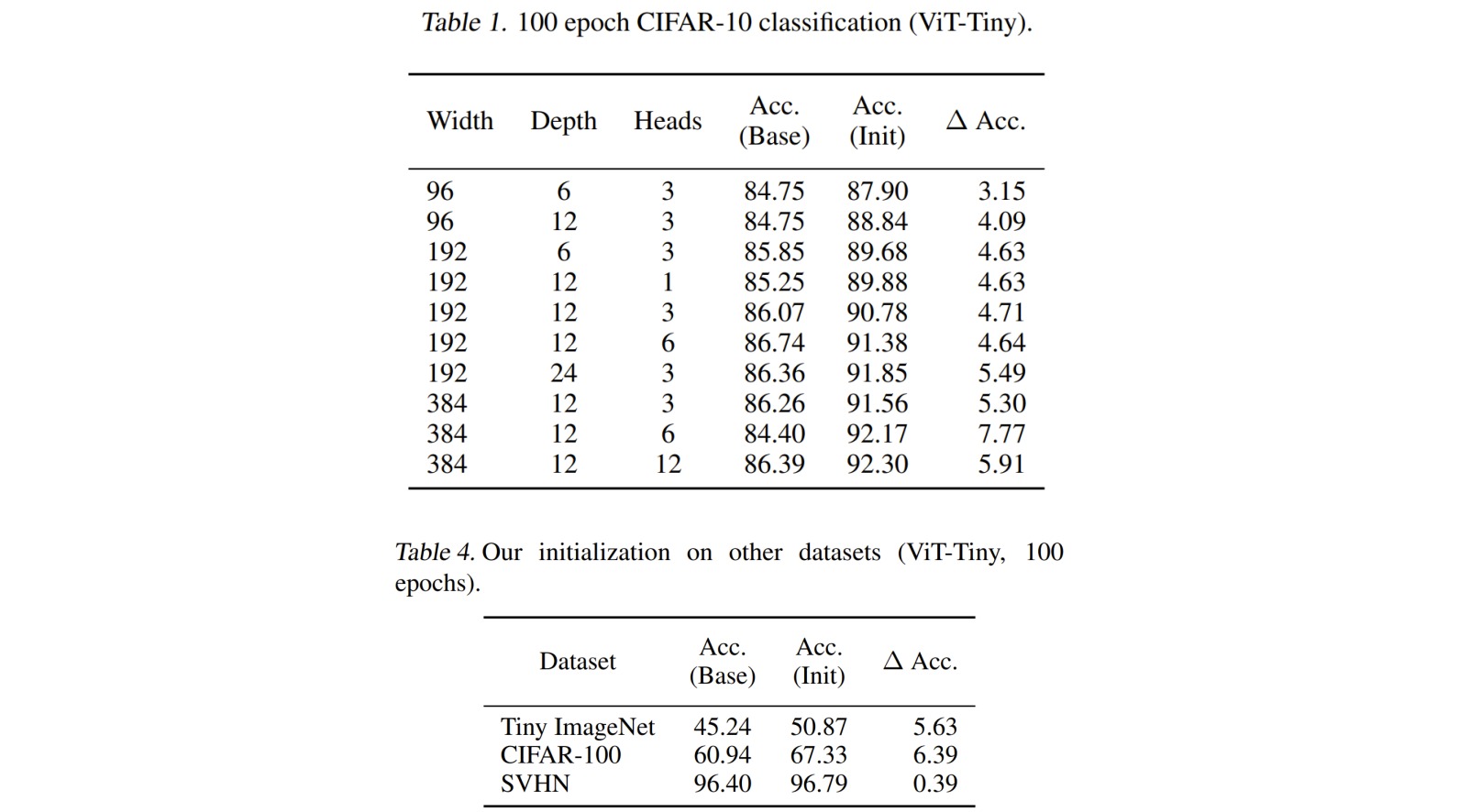
\[O^h = AXW_VW_{proj} \in R^{n \times d}\]对ImageNet上预训练的ViT-Tiny模型的注意力图进行可视化,发现$W_QW_K^T$的对角线在许多情况下是显著正的。类似地,$W_VW_{proj}$的乘积往往具有明显的负对角线。这表明$W_Q,W_K$可能是“相同”的低秩随机正规矩阵,因为这样的矩阵近似半正交。即对任意$Z \sim N(0, I/k)\in R^{d \times k}$,近似有$ZZ^T\approx I$。

根据上述观察的结论,可以针对$W_QW_K^T$以及$W_VW_{proj}$进行模仿初始化。把$W_QW_K^T$初始化为单位矩阵$I$,可以把两个矩阵设置为相同的随机正规矩阵:
\[W_Q=W_K\sim N(0, I/k)\]把$W_VW_{proj}$初始化为负单位矩阵$-I$,可以设置:
\[Z \sim N(0, I/d),W_V=Z,W_{proj}=-Z\]上述初始化设置的原理是从$N(0, I/k)$随机采样的任意两个向量都是正交且归一化的,即:
\[\begin{aligned} <x,y> &= \sum_{i=1}^kx_iy_i = k\times \frac{1}{k}\sum_{i=1}^kx_iy_i\\ &\approx k\times\mathbb{E}_{x\sim p(x),y\sim p(x)} \left[ xy \right] \\ &= k\times\mathbb{E}_{x\sim p(x)} \left[ x \right]\mathbb{E}_{y\sim p(x)} \left[ y \right]\\ &= 0 \\ ||x||^2 &= \sum_{i=1}^kx_i^2 = k\times \frac{1}{k}\sum_{i=1}^kx_i^2 \\ &\approx k\times\mathbb{E}_{x\sim p(x)} \left[ x^2 \right] \\ & = k\times (\mathbb{E}_{x\sim p(x)}^2 \left[ x \right]+\text{Var}_{x\sim p(x)} \left[ x \right])\\ &= k \times \frac{1}{k} = 1 \end{aligned}\]然而无论如何缩放随机正规矩阵,对角线上和对角线外噪声的大小之间的比率都保持不变。为了在对角线部分获得更多的灵活性,不妨初始化为:
\[\begin{aligned} W_QW_K^T \approx & \alpha_1Z_1+\beta_1 I\\ W_VW_{proj} \approx & \alpha_2Z_2-\beta_2 I \end{aligned}\]其中$Z_i \sim N(0, I/d),\alpha_i,\beta_i \in [0,1]$。为了恢复$W_V,W_{proj}$,采用奇异值分解:
\[\begin{aligned} &\alpha_2Z_2-\beta_2 I = U_2\Sigma_2V_2^T \\ &W_V=U_2\Sigma_2^{1/2},W_{proj}=\Sigma_2^{1/2}V_2^T \end{aligned}\]为了恢复低秩形式的$W_V,W_{proj}$,采用奇异值分解:
\[\begin{aligned} &\alpha_1Z_1+\beta_1 I = U_1\Sigma_1V_1^T \\ &W_Q=U_1[:,:k]\Sigma_1[:k,:k]^{1/2} \\ &W_K=V_1[:,:k]\Sigma_1[:k,:k]^{1/2} \end{aligned}\]根据超参数搜索,实验中设置$\alpha_1=\beta_1=0.7, \alpha_2=\beta_2=0.4$。

实验结果表明,所提初始化技术在提高小规模图像识别任务的性能方面特别有效。