DynOPool: 学习最优感受野的动态优化池化.
本文提出了一种简单有效的动态优化池化 (Dynamically Optimized Pooling operation, DynOPool),它通过学习每一层感受野的最佳大小和形状来调整特征映射的空间尺寸。深度神经网络中任何类型的空间尺寸调整模块都可以用DynOPool操作以最小的成本替换。此外,DynOPool通过引入一个限制计算成本的附加损失项来控制模型的复杂度。
1. 池化层的感受野
感受野的大小和形状决定了网络如何聚集本地信息,并对模型的整体性能产生显著影响。神经网络中的卷积和池化运算的核大小和步长都会影响感受野。然而现有方法产生的是具有固定大小和形状的感受野,不擅长捕捉以下信息:
- 不对称分布的信息:最佳感受野的形状会根据数据集中固有空间信息的不对称性而改变,在大多数情况下这种固有的不对称性是不可测量的。此外通过对输入图像的大小进行预处理调整也会导致信息不对称,比如图像的长宽比经常被调整以满足模型的输入规格。
- 密集分布或稀疏分布信息:卷积网络通过级联的方式聚合局部信息来学习图像的复杂表示,而局部信息的重要性取决于图像的属性。例如当一个图像被模糊化时,大多数有意义的微观模式(如物体的纹理)会被抹去,此时最好在早期网络层中扩展感受野以捕捉全局信息;如果一幅图像在局部细节中包含大量类特定的信息,则识别局部信息将会更加重要。
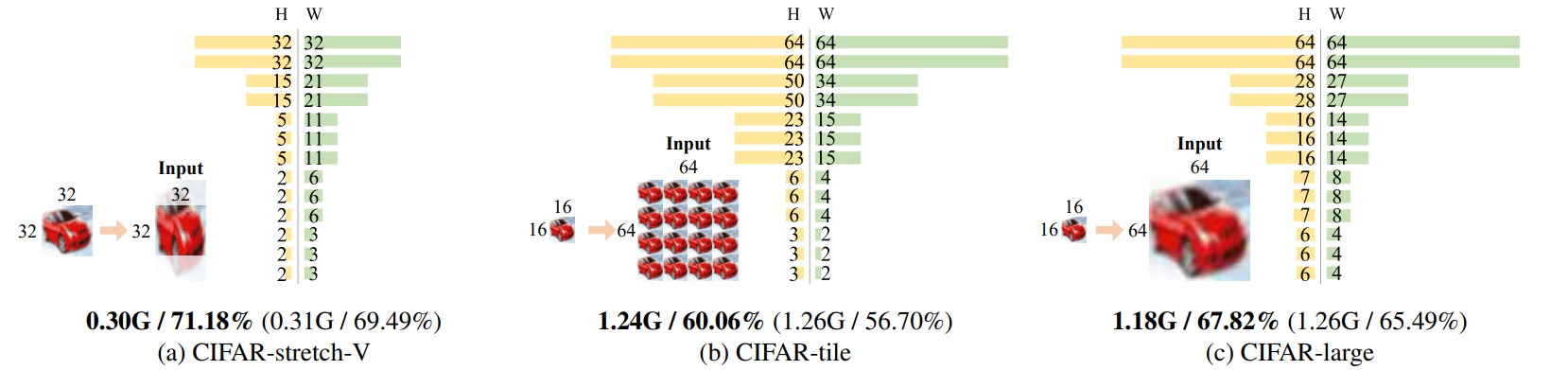
作者通过CIFAR-100构造了三个不同的合成数据集:(a) 随机裁剪经过垂直拉伸的图像;(b) 把缩小的图像平铺为4×4网格;(c) 直接放大缩小的图像。作者统计了经过本文所提方法生成的网络不同层中的最优感受野大小,发现感受野应具有不同的大小和形状以提取更具有价值的信息。
2. 动态优化池化
动态优化池化(DynOPool)是一个可学习的空间尺寸大小调整模块,可以替代标准的尺寸调整操作(比如最大池化层)。该模块在数据集上学习感受野的最佳比例因子,从而将网络的中间特征图调整为适当的大小和形状。

记输入特征的空间尺寸为$H_{in} \times W_{in}$,给定缩放因子$r=(r_h,r_w)$,DynOPool首先把特征图划分为$H_{out} \times W_{out}$个栅格,有
\[\begin{aligned} H_{out} &= \lfloor H_{in} \cdot r_h \rceil \\ W_{out} &= \lfloor W_{in} \cdot r_w \rceil \end{aligned}\]对于某个栅格中心$p=(p_h,p_w)$,构造四个查询点$q=(p_h ± \delta_h,p_w± \delta_w)$,四个查询点的像素值通过双线性插值获得。则该栅格的输出可以通过四个查询点的聚合函数构造,本文选择最大池化操作。
DynOPool通过参数$r=(r_h,r_w)$控制感受野的大小,通过参数$\delta=( \delta_h,\delta_w)$控制感受野的形状。这些参数都是从数据集中学习得到的。由于通过参数$r$构造输出特征可能出现非整数的空间尺寸,因此引入四舍五入运算\(\lfloor \cdot \rceil\),并通过梯度停止算子$sg(\cdot)$实现可微量化技巧:
\[\begin{aligned} H_{out} &= \lfloor H_{in} \cdot r_h \rceil +H_{in} \cdot r_h-sg(H_{in} \cdot r_h) \\ W_{out} &= \lfloor W_{in} \cdot r_w \rceil + W_{in} \cdot r_w - sg(W_{in} \cdot r_w) \end{aligned}\]参数$r$通常是比较小的数,为了减少优化困难,对其重参数化为$\alpha = [\alpha_h,\alpha_w]$:
\[[\alpha_h,\alpha_w] = [r_h^{-1},r_w^{-1}]\]则完整的前向传播与梯度更新过程为:

为了防止DynOPool学习到的特征分辨率过大,作者在损失函数中额外引入了约束第$t$轮训练中网络的特征图尺寸比例和GMACs(统计网络中的加乘操作数)的项:
\[\mathcal{L}_{GMACs} = \sum_{l=1}^N \frac{H_{out}^{t^{(l)}} \cdot W_{out}^{t^{(l)}}}{H_{out}^{0^(l)} \cdot W_{out}^{0^{(l)}}} \cdot GMACs[l]\]

