AlphaTensor:通过强化学习发现更快的矩阵乘法算法.
本文介绍了AlphaTensor,AlphaTensor建立在AlphaZero的基础上,用于为矩阵乘法等基本算法发现正确、高效的算法。
几个世纪以来,数学家们一直认为标准的矩阵乘法算法是效率最高的算法。但在1969年,德国数学家沃尔克·斯特拉森证明了确实存在更好的算法。通过研究$2\times 2$的矩阵,他发现了一种巧妙的方法,可以将矩阵的元素组合起来。与标准算法相比,Strassen的算法少用了一个标量乘法,从而产生更快的算法。


尽管如此,对于$3\times 3$及更大的矩阵,发现更快的直接计算的矩阵乘法算法仍然是相当困难的。为挑战这一问题,AlphaTensor把寻找矩阵乘法算法的问题转化为一个单人游戏。注意到矩阵乘法可以被写作一个通用的形式,即首先计算一系列两个矩阵元素线性组合的乘积$h_1,…,h_R$(对应$R$次乘法),则输出矩阵的每个元素都能表示为这些乘积的线性组合。并且所有线性组合的系数取值都为$(-1,0,1)$。

在这个游戏中,agent每次生成一次乘法的线性组合系数$u^r,v^r,w^r$,并根据这些系数累积输出结果,直至输出结果为矩阵乘法的正确结果。训练目标为尽可能减少乘法次数,并减少在指定硬件设备上的推理时间。

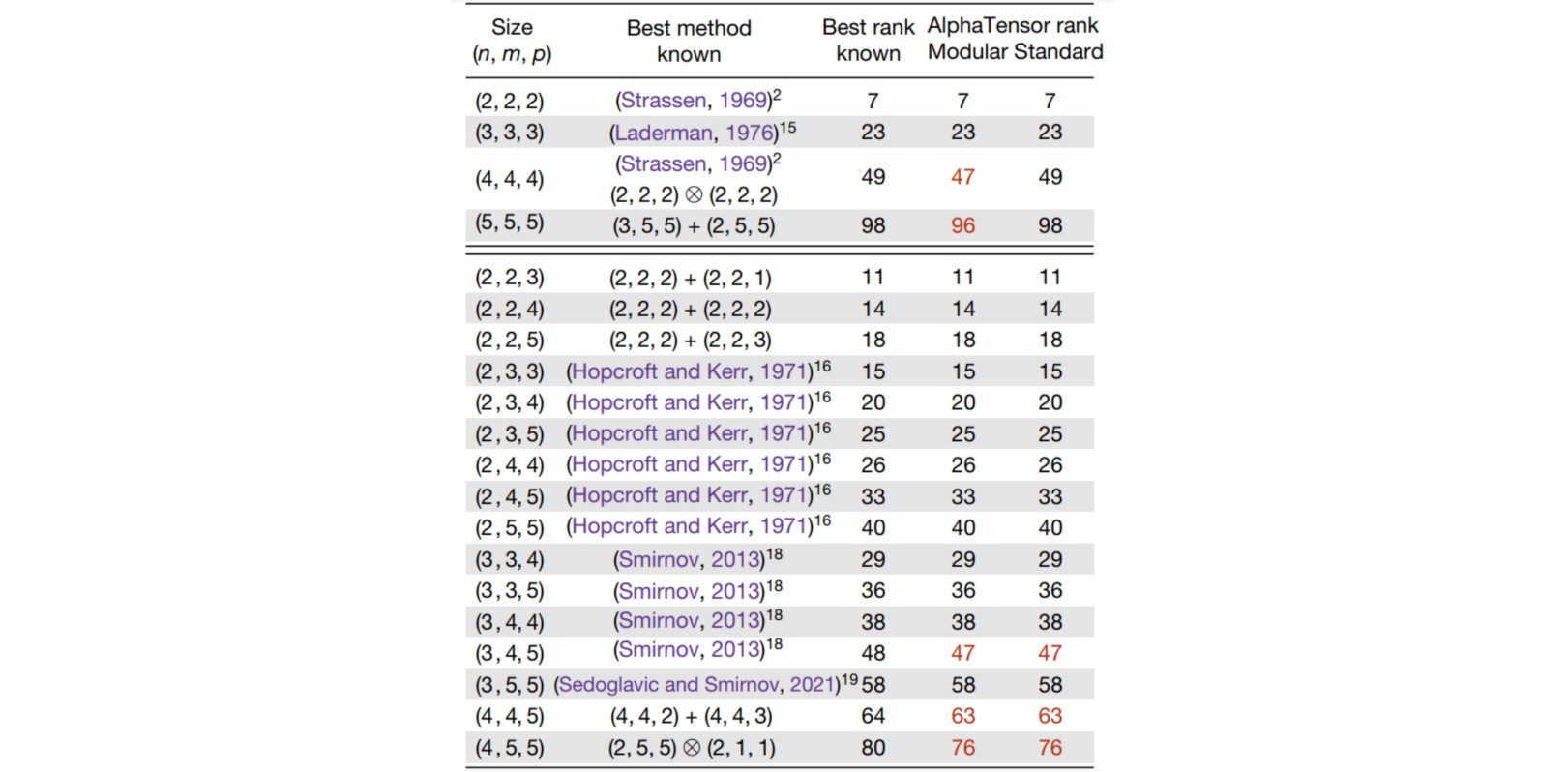
下图给出了对于$n\times m$矩阵与$m\times p$矩阵的矩阵乘法运算,迄今为止人类发现的最少乘法运算次数与AlphaTensor发现的结果比较。标红的结果表明,对于一些尺寸的矩阵乘法,AlphaTensor发现了具有更少乘法次数的矩阵运算步骤。比如$4\times 5$矩阵与$5\times 5$矩阵的标准乘法需要$100$次乘法运算,人类迄今为止发现的优化运算需要$80$次乘法,而AlphaTensor发现的算法只需要$76$次乘法。
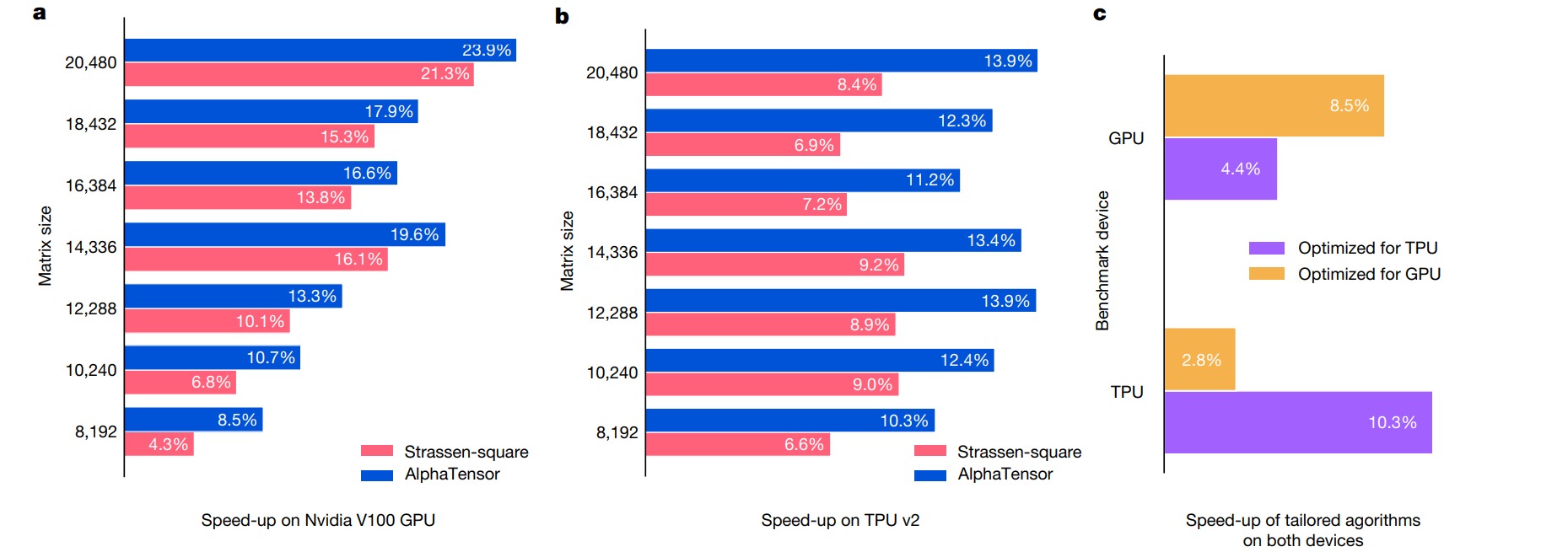
上述算法可以被自然地推广到分块矩阵乘法中,并可以递归地应用到每一个矩阵块乘法内,从而很大程度上减少大规模矩阵乘法算法所需的乘法次数。作者实测了把矩阵进行$4\times 4$分块后进行优化的乘法,结果表明AlphaTensor发现的算法确实能够提高乘法的推理速度。此外,由于训练过程考虑到实际硬件设备的速度,因此所发现的算法是与硬件相匹配的。