通过不变和扩散的实例特征实现无监督嵌入学习.
本文作者指出,相同的图像经过简单的数据增强后,特征具有不变性(Invariant),即分布在相似的特征空间中;对于不同的图像,其特征具有扩散性(Spreading),特征应尽可能地分开。

本文采用个体判别任务,对于一批样本进行数据增强,把样本$x$的增强样本\(\hat{x}\)视为正样本,其余所有样本视为负样本;对于正样本增加数据增强的特征不变性,对于负样本减小被当作其他样本的概率:
\[\mathcal{L}_{\text{InvaSpread}} = -\sum_i \log \frac{\exp(f_i^T\hat{f}_i/\tau)}{\sum_{k=1}^N\exp(f_k^T\hat{f}_i/\tau)}-\sum_i \sum_{j\neq i} \log(1- \frac{\exp(f_i^Tf_j/\tau)}{\sum_{k=1}^N\exp(f_k^Tf_j/\tau)})\]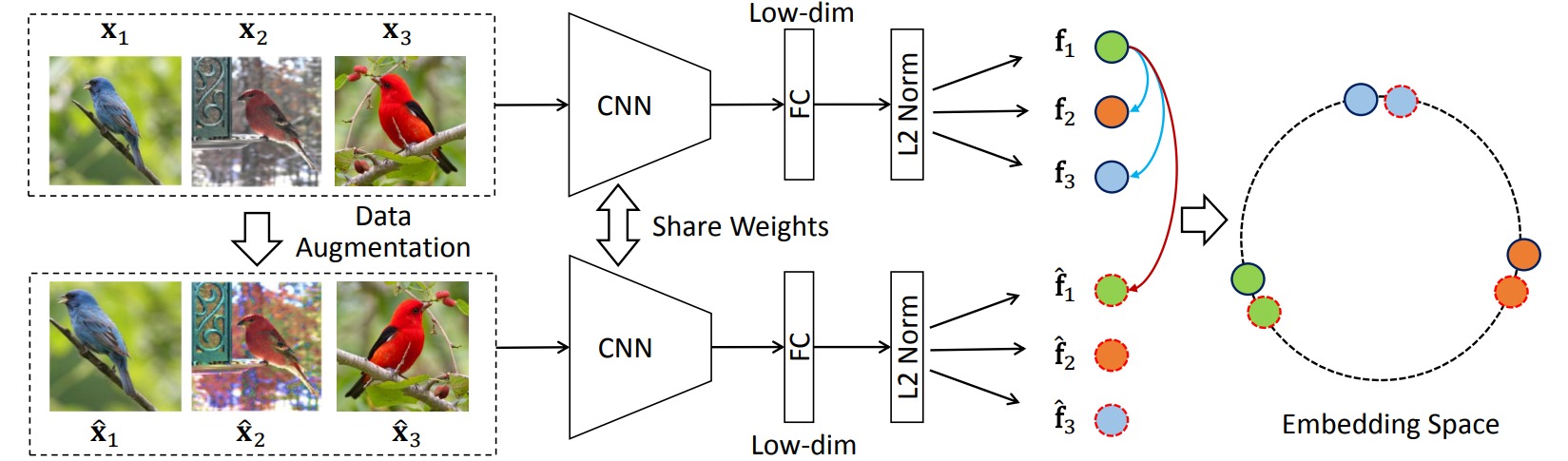
class BatchCriterion(nn.Module):
''' Compute the loss within each batch
'''
def __init__(self, T):
super(BatchCriterion, self).__init__()
self.T = T
def forward(self, x, x_hat)
batchSize = x.size(0)
#get positive innerproduct
pos = (x*x_hat).sum(1).div_(self.T).exp_() # [B, 1]
#get all innerproduct
all_prob = torch.mm(x,x_hat.t()).div_(self.T).exp_() # [B, B]
all_div = all_prob.sum(0).view(-1, 1) # [B, 1]
#positive probability
lnPmt = torch.div(pos, all_div) # [B, 1]
#positive loss
lnPmt.log_()
lnPmtsum = lnPmt.sum(0)
#get negative innerproduct
intra_prob = torch.mm(x,x.t()).div_(self.T).exp_() # [B, B]
#negative probability
Pon_div = intra_prob.sum(0).view(-1, 1) # [B, 1]
lnPon = torch.div(intra_prob, Pon_div) # [B, B]
lnPon = -lnPon.add(-1)
#remove the pos term
lnPon.log_()
mask = torch.ones_like(lnPon)-torch.eye(batchSize)
lnPon = lnPon * mask
#negative loss
lnPonsum = lnPon.sum()
loss = - (lnPmtsum + lnPonsum)/batchSize
return loss


