元伪标签.
- paper:Meta Pseudo Labels
自训练(self-training)是半监督学习中的常用方法,即首先通过有标签样本初始化训练一个教师网络,然后通过该网络预测无标签样本的伪标签,并选择其中置信度最高的一批样本按伪标签进行标注,通过扩增的数据集训练一个学生网络。通过迭代上述过程直至所有未标注样本都被指定一个伪标签。
元伪标签方法根据学生网络在标注数据集上的反馈表现持续地调整教师网络。教师网络和学生网络是并行训练的,教师网络旨在学习生成更好的伪标签,学生网络旨在通过伪标签进行学习。

记教师网络和学生网络的参数分别为$\theta_T,\theta_S$,则元伪标签在标注数据集上的损失定义为:
\[\mathop{\min}_{\theta_T} \mathcal{L}_s(\theta_S(\theta_T)) = \mathop{\min}_{\theta_T} \sum_{(x^l,y) \in \mathcal{X}} \text{CE}[y,f_{\theta_S(\theta_T)}(x^l)]\]其中学生网络参数$\theta_S$是教师网络参数$\theta_T$的函数:
\[\theta_S(\theta_T) = \mathop{\arg \min}_{\theta_S} \mathcal{L}_u(\theta_S,\theta_T) = \mathop{\arg \min}_{\theta_S} \sum_{x^u \in \mathcal{U}} \text{CE}[f_{\theta_T}(x),f_{\theta_S}(x)]\]上式直接求解比较困难,通过$\theta_S$的单步梯度更新代替\(\mathop{\arg \min}_{\theta_S}\)算符:
\[\theta_S(\theta_T) \approx \theta_S - \eta_S \cdot \nabla_{\theta_S} \mathcal{L}_u(\theta_S,\theta_T)\]则损失函数为:
\[\mathop{\min}_{\theta_T} \mathcal{L}_s(\theta_S(\theta_T)) \approx \mathop{\min}_{\theta_T} \mathcal{L}_s(\theta_S - \eta_S \cdot \nabla_{\theta_S} \mathcal{L}_u(\theta_S,\theta_T))\]当伪标签采用软标签形式,上述目标是可微的,两个网络可以通过梯度下降算法端到端地更新参数。
上述优化过程实际上是在迭代地训练两个模型:
- 更新学生网络:给定未标记数据\(x^u \in \mathcal{U}\),生成伪标签\(f_{\theta_T}(x^u)\),通过单步梯度下降更新学生网络参数$\theta_S$:$\theta_S’ = \theta_S - \eta_S \cdot \nabla_{\theta_S} \mathcal{L}_u(\theta_S,\theta_T)$
- 更新教师网络:给定已标记数据\((x^l,y) \in \mathcal{X}\),更新教师网络参数$\theta_T$:\(\theta_T' = \theta_T - \eta_T \cdot \nabla_{\theta_T} \mathcal{L}_s(\theta_S - \eta_S \cdot \nabla_{\theta_S} \mathcal{L}_u(\theta_S,\theta_T))\)
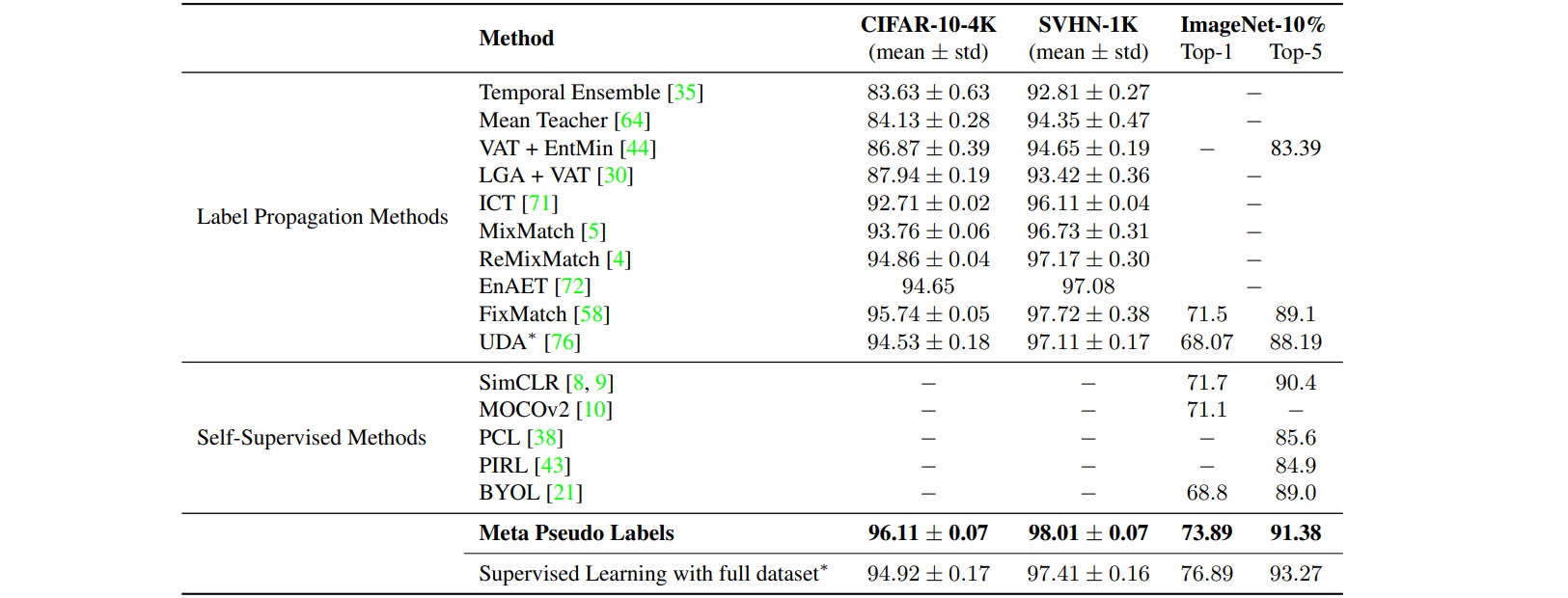
作者报告了不同方法在图像分类任务中的表现: