Self-Organizing Map.

自组织映射(self-organizing map, SOM)又称自组织特征映射、Kohonen网络，是一种竞争学习型的无监督神经网络。

SOM将高维数据映射到具有简单几何结构和相互关系的低维离散空间(通常是$2$维)中，映射过程能够维持输入数据在高维空间的拓扑结构；这是通过邻域函数(neighborhood function)的约束来实现的。

不同于一般神经网络的梯度更新，SOM使用竞争学习(competitive learning)策略，依靠神经元之间的相互竞争逐步优化网络。

本文目录：

构建SOM模型
SOM的训练过程
SOM的实现细节
SOM的实际应用

1. 构建SOM模型

SOM具有两层网络结构。输入层具有$n$个节点，对应输入样本的$n$个特征维度。输出层也叫竞争层，其节点分布通常具有较低的维度(常用$2$维)。图示给出了具有$X\times Y$个节点的竞争层。

从后面的学习过程可以看出，竞争层的每一个节点也用一个维度为$n$的特征向量表示。因此每一个节点可以看作是一个“聚类中心”，SOM的学习过程便是将每一个输入数据映射到竞争层上的一个节点上，并使得在输入空间中比较接近的输入数据映射到竞争层节点的几何位置也比较接近。

竞争层的节点数决定了SOM的规模，应具有足够多的节点数以保证模型的准确率与泛化能力。二维竞争层应具有的最少节点数量的经验公式：

\[X = Y = \lceil \sqrt{5\sqrt{n}} \rceil\]

x = math.ceil(np.sqrt(5 * np.sqrt(n)))

2. SOM的训练过程

SOM的权重存储了竞争层每个节点的特征，记为$W \in \Bbb{R}^{X\times Y \times n}$。

SOM的训练过程如下：

权重初始化：通过初始化函数init_weight将SOM竞争层的权重初始化为$W \in \Bbb{R}^{X\times Y \times n}$；
样本选择：训练过程类似于随机梯度下降，每次选择一个数据样本$x$进行学习；
距离计算：通过距离函数(通常是欧氏距离)计算样本$x$与竞争层每一个节点之间的距离；
竞争过程：选择与样本$x$距离最近的节点$(i,j)$，将其作为优胜节点(winner node)，也称最佳匹配单元(best matching unit)；
自组织过程：根据邻域半径sigma确定优胜邻域$\sigma$，并通过邻域函数neighborhood_function计算每个节点更新的幅度$g$(通常越靠近优胜节点，更新幅度越大)；
权重更新：通过学习率$\eta$更新优胜邻域内的节点权重：

\[W = W + \eta g \cdot (x-W)\]

def traim_SOM(X, Y, M, # 竞争层节点数 X×Y；特征维度 M
              N_epoch, data,
              learning_rate = 0.5, sigma = 0.5):
# 总训练迭代数 = 训练轮数×样本数量
N_iter = N_epoch * data.shape[0]
# 权重初始化
weights = init_weight(X, Y, M, data)

for n_epoch in range(N_epoch):
    # 打乱样本
    index = np.random.permutation(np.arange(data.shape[0]))
    for n_iter, id in enumerate(index):
        x = data[id]
        # 计算学习率
        t = data.shape[0]*n_epoch+n_iter
        eta = get_learning_rate(learning_rate, t, N_iter)
        # 计算优胜节点
        winner = get_winner_node(x, weights)
        # 计算邻域函数
        new_sigma = get_learning_rate(sigma, t, N_iter)
        g = neighborhood_function(X, Y, winner, new_sigma)
        g = eta * g
        # 权重更新
        weights = weights + np.expand_dims(g,-1)*(x-weights)

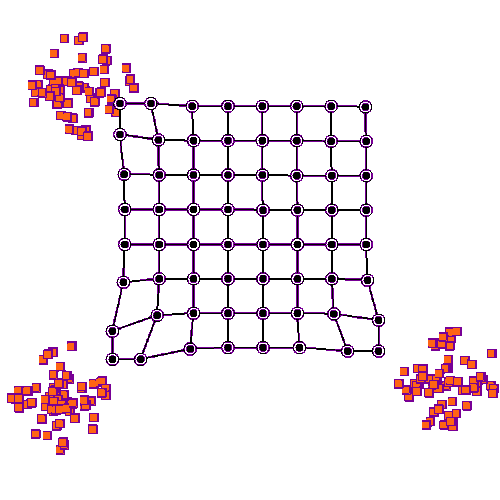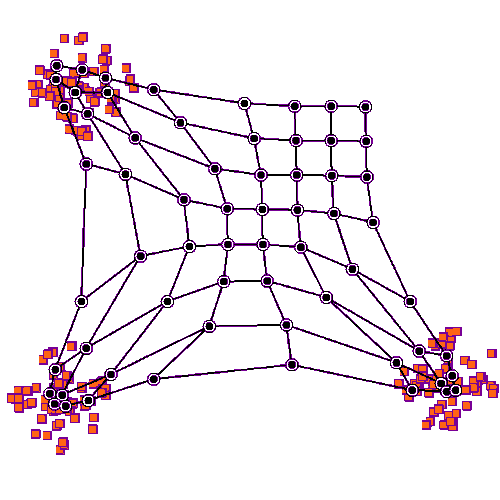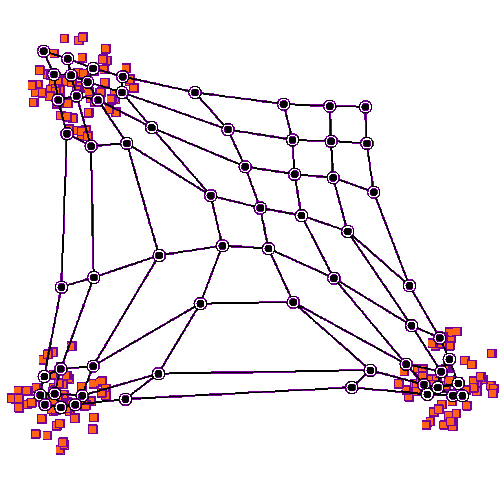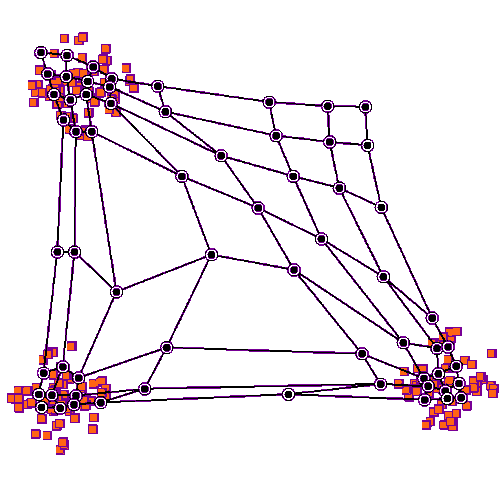
通过上述训练，优胜节点会逐渐靠近其对应的输入样本所在的空间位置，优胜节点拓扑结构的邻域节点也被类似的更新。

一种解释方法是把竞争层上的节点权重看作输入空间的指针，它们形成对训练样本分布的离散近似。更多节点指向的区域，训练样本分布更密集；而较少节点指向的区域，样本分布比较稀疏。

3. SOM的实现细节

(1) 权重初始化

SOM的权重初始化有三种不同的方法：

① 随机初始化 Random initialization

随机初始化是指把权重随机地初始化为一些较小的值，适用于对输入数据有很少或没有任何先验知识的情况。一般地，随机初始化后会对权重进行归一化。

def init_weight(X, Y, M, data):
    rng = np.random.RandomState(seed=42)
    weights = rng.rand(X,Y,M)*2-1
    weights /= np.linalg.norm(weight, axis=-1, keepdims=True)
    return weights

② 随机样本初始化 Initialization using initial samples

随机样本初始化是指随机选择$X \times Y$个样本赋值给SOM的权重。这种初始化方法使得初始时刻网络节点与输入数据的拓扑结构就具有一定的相似性。

③ 线性初始化 Linear initialization

线性初始化是指使用PCA对权重进行初始化。

具体地，计算出数据集的协方差矩阵的特征值和特征向量，选择最大的两个特征值对应的特征向量，将其作为基向量按照线性映射为新的向量。

假设两个特征向量分别为$(x_1,x_2,…,x_n)$和$(y_1,y_2,…,y_n)$，对区间$[-1,1]$等比例分别取$X$和$Y$个值，则可得到两个特征向量的$X\times Y$个线性组合，将其作为权重的初始化。

def init_weight(X, Y, M, data):
    weights = np.zeros([X,Y,M])
    values, vectors = np.linalg.eig(np.cov(np.transpose(data)))
    order = np.argsort(-values)
    for i, c1 in enumerate(np.linspace(-1,1,X)):
        for j, c2 in enumerate(np.linspace(-1,1,Y)):
            weights[i,j] = c1*vectors[order[0]]+c2*vectors[order[1]]
    return weights

如果数据集的整体分布近似数据集的第一主成分方向(数据集近似线性)，则可以采用线性初始化。对于非线性数据集，通常随机初始化是一个更好的选择。

(2) 计算优胜节点

优胜节点是指与样本特征相似度最高(距离最近)的竞争层节点。

在预处理输入样本时可以考虑进行标准化(均值为$0$，标准差为$1$)；这样有助于使每个特征对于计算相似度的贡献相同。

mu = np.mean(data,axis=0,keepdims=True)
std = np.std(data,axis=0,keepdims=True)
data = (data-mu)/std
x = data[id]

def get_winner_node(x, weights):
    dis = np.expand_dims(x,aixs=(0,1))-weights
    dis = np.linalg.norm(dis, axis=-1)
    index = np.where(dis==np.min(dis))
    return (index[0][0], index[1][0])

(3) 计算邻域函数

邻域函数用来确定优胜节点对其余所有节点的影响，以权重的形式体现。距离优胜节点越近的节点对应的权重越高，距离优胜节点越远的节点对应的权重越低。权重影响更新幅度，因此优胜邻域内的节点具有较大的更新程度。

常用的邻域函数包括：

① Gaussian

高斯函数是一个连续函数，因此通过高斯函数选定的邻域也是连续的。参数sigma控制高斯函数的形状，即有效邻域的范围。当sigma很小时，只有优胜节点处权重接近$1$，其余节点权重都接近$0$。当sigma很大时，所有节点都具有较大的更新幅度。

假设优胜节点为$(c_x,c_y)$，则任意节点$(i,j)$处的高斯邻域函数定义为：

\[g(i,j) = e^{-\frac{(c_x-i)^2}{2\sigma^2}}e^{-\frac{(c_y-j)^2}{2\sigma^2}}\]

def neighborhood_function(X, Y, winner, sigma):
    xx, yy = np.meshgrid(np.arange(X), np.arange(Y)) # xx,yy -> [Y,X]
    ax = np.exp(-np.power(xx-winner[0],2)/(2*sigma*sigma)) # ax -> [Y,X]
    ay = np.exp(-np.power(yy-winner[1],2)/(2*sigma*sigma)) # ay -> [Y,X]
    return (ax*ay).T

② Bubble

Bubble函数是一个矩形函数，表示在优胜邻域内的节点都赋予权重$1$，在邻域外的节点都赋予权重$0$。Bubble函数相当于硬阈值的高斯函数。

假设优胜节点为$(c_x,c_y)$，邻域半径为$\sigma$，则任意节点$(i,j)$处的高斯邻域函数定义为：

\[g(i,j) = \begin{cases} 1, & c_x-\sigma\leq i\leq c_x+\sigma \text{ and } c_y-\sigma\leq j\leq c_y+\sigma \\ 0, & \text{others} \end{cases}\]

此时邻域半径$\sigma$只有一些离散的取值有意义，比如取值范围$[1,2)$均表示取与优胜节点距离为$1$的节点。

def neighborhood_function(X, Y, winner, sigma):
    x, y = np.range(X), np.range(Y)
    ax = np.logical_and(x>winner[0]-sigma, x<winner[0]+sigma)
    ay = np.logical_and(y>winner[1]-sigma, y<winner[1]+sigma)
    return np.outer(ax, ay)

(4) 学习率和邻域半径的衰减

随着迭代次数的增大，学习率$\eta$应该逐步减少，以促进模型的收敛。邻域半径$\sigma$也应该逐渐减小，其目的是更精细地调整权重。

若记$T$为总迭代次数，$t$为当前迭代次数，则参数衰减公式表示为：

\[\eta = \frac{\eta_0}{1+\frac{t}{T/2}}, \quad \sigma = \frac{\sigma_0}{1+\frac{t}{T/2}}\]

def get_learning_rate(learning_rate, t, N_iter)
    return learning_rate/(1+t/(N_iter/2))

4. SOM的实际应用

在实践中，可以通过minisom库快速构造SOM模型。

# pip install minisom
import minisom

SOM模型定义如下：

som = minisom.MiniSom(X,Y,M,
                      sigma=sig,
                      learning_rate=learning_rate,
                      neighborhood_function='gaussian')

创建SOM模型时已经默认随机初始化网络权重。也可采用其他初始化方法：

som.random_weights_init(X_train)：随机样本初始化
som.pca_weights_init(X_train)：PCA初始化

SOM模型的训练语句如下：

som.train_batch(X_train, max_iter, verbose=False) # 逐个样本进行迭代
som.train_random(X_train, max_iter, verbose=False) # 随机选样本进行迭代

训练完成后，可以获取以下参数：

som.get_weights()：获取网络的权重。
som.activate(X)：获取样本$X$的节点激活图，数值越小的节点表示与样本相似度越高。
som.winner(X)：获取样本$X$的优胜节点。
som.quantization(X)：获取样本$X$的优胜节点对应的权重。

SOM模型是一类无监督的神经网络，也可以被用于聚类、降维和分类任务中。下面以minisom为例，说明SOM模型的一些应用。

(1) 可视化

使用SOM模型进行数据的聚类和降维可视化主要通过构造U-Matrix实现。

U-Matrix全称是unified distance matrix。U-Matrix是通过计算每个节点与其邻域(通常是$8$邻域)节点之间的权重距离得到的。在矩阵中较小的值表示该节点与其邻域节点在输入空间中比较接近；在矩阵中较大的值表示该节点与其邻域节点在输出空间中相离较远。 U-matrix可以看作输入空间中样本的概率密度在二维平面上的映射。

对于训练好的模型som，可视化其U-Matrix：

heatmap = som.distance_map()  # 生成U-Matrix
plt.imshow(heatmap, cmap='bone_r')
plt.colorbar()

图中颜色较深(数值较大)的点表示该节点与邻域节点之间的距离较大，可以看作聚类的分界线或者分类的边界。

(2) 分类

SOM模型虽然是无监督的神经网络，也可以引入标签信息。对于训练好的模型som，通过下式标注对应的标签：

winmap = som.labels_map(X_train,y_train)

上式不仅将训练集中的所有样本映射到对应的节点位置，并且给每个节点位置包含的样本的类别信息。通过简单的投票，可以为每个节点指定一个具体的类别。

对于一个新的样本，将它映射到某一个节点时，该样本的预测类别则是对应节点的类别。

results = som.classify(x_new, winmap)