统一神经网络的非局部模块.
捕获空间像素或时间帧之间的长距离时空依赖性在计算机视觉任务中起着至关重要的作用。卷积神经网络需要堆叠多个卷积扩大感受野以建立远程依赖,但是这样做会增加成本和过拟合的风险,而且堆叠卷积层不一定能有效增加感受野。
Nonlocal块通过创建一个包含每个成对位置之间关系的密集亲和矩阵,然后使用该矩阵作为注意力图通过加权均值聚合特征。但是该方法设计大量特征对,包含太多噪声。本文作者为Nonlocal块的模型设计提供了一个新的视角,将它们视为在全连接图上生成的一组图过滤器。
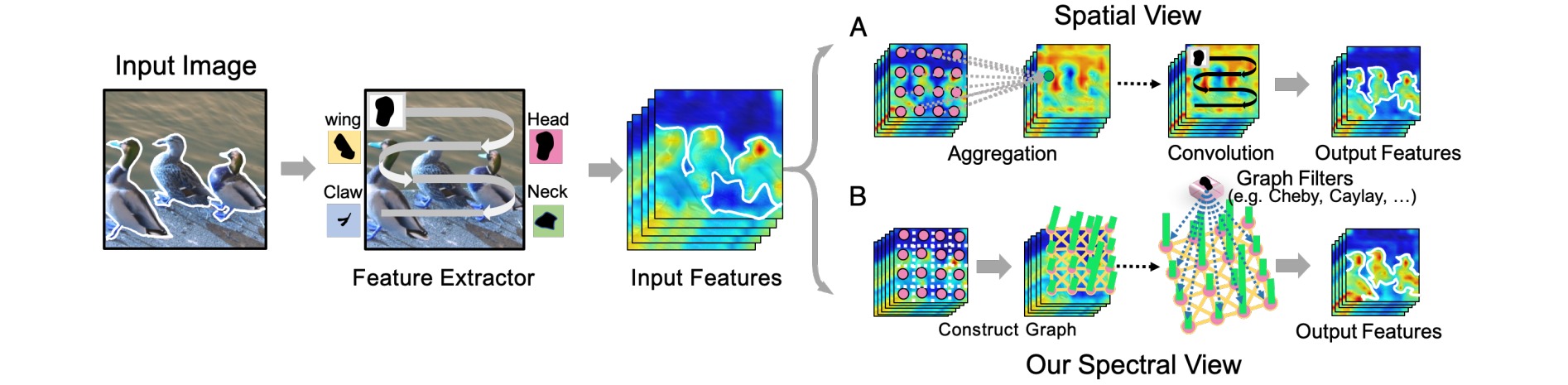
首先基于输入特征构建全连接图(包含不同位置的相似性),然后使用可学习的图滤波器过滤特征。在切比雪夫图滤波器的帮助下,在新视角下推导出了基于非局部块的统一公式,并进一步设计了谱非局部模块(spectral Nonlocal, SNL)。
Nonlocal块计算每个位置的特征与所有可能位置的特征之间的加权和:
\[F(X_{i,:})=\frac{ \sum_j f\left(x_{i,:}, x_{j,:}\right) g\left(x_{j,:}\right)}{\sum_j f\left(x_{i,:}, x_{j,:}\right) }\]其中$f(·)$是具有有限$F$范数的亲和核,$g(·)$是一个线性嵌入。在将NL块插入到网络结构中时,加入了一个权重矩阵$W$的线性变换和一个残差连接:
\[Y_{i,:} = X_{i,:}+F(X_{i,:})W\]写出上式的矩阵形式,并将参数矩阵$W$分解:
\[Y = X+F(X)W= X+AZW_{s1}W_{s2}\]其中亲和矩阵$A=D_M^{-1}M$,$M$由像素之间的成对相似性组成$M_{ij}=<X_{i,:},X_{j,:}>$,$D_M$是$M$的每个顶点的加权度。$Z=XW_Z$是特征图。不妨把$W_{s1}$看作一组图滤波器$g_{\theta}$,则可以在频域设计NL块:
\[Y = X+\mathcal{F}(A,Z,W_{s1})W_{s2} = X+\mathcal{F}(A,Z,g_{\theta})W_{s2}\]Nonlocal与在全连通图$G$的图域下通过一组图滤波器$g_θ$对信号$Z$进行滤波相同:
\[\mathcal{F}(A,Z,g_{\theta}) = [O_{z_1*\mathcal{G}g_{\theta}^1},\cdots,O_{z_i*\mathcal{G}g_{\theta}^i},\cdots,O_{z_C*\mathcal{G}g_{\theta}^C}]\]nonlocal通过卷积算子对特征进行过滤,而上式学习图滤波器以获取谱域下的特征。为证实图谱域的存在,要求图拉普拉斯$L$(滤波器)应该是对角化的,并且不包含复特征值和特征向量。因此亲和度矩阵 $A$ 应该是对称的。具体来说,通过将图谱滤波器设置为一组对角参数矩阵$\Omega^i$:
\[O_{z_i*\mathcal{G}g_{\theta}^i} = U\Omega^iU^Tz_i\]使用切比雪夫多项式将$Ω^i$中的参数化简为$K$($K$为多项式的阶数,且$K< <N$),假设输入输出都有一个通道数,用$K$阶切比雪夫多项式近似的图滤波器的参数矩阵被公式化为:
\[\begin{gathered} \mathcal{F}(\boldsymbol{A}, \boldsymbol{Z})=\sum_{k=0}^{K-1} \hat{\theta}_k T_k(\tilde{\boldsymbol{L}}) \boldsymbol{Z} \\ \text { s.t. } \quad T_k(\tilde{\boldsymbol{L}})=2 \tilde{\boldsymbol{L}} T_{k-1}(\tilde{\boldsymbol{L}})-T_{k-2}(\tilde{\boldsymbol{L}}) \\ \tilde{L}=2 L / \lambda_{\max }-I_n, T_0(\tilde{L})=I_n, T_1(\tilde{L})=\tilde{L} \end{gathered}\]注意亲和力矩阵 $A$ 受输入特征 $X$ 的影响,而不是使用固定的图结构。因此,当它们的所有图拉普拉斯算子都是归一化图拉普拉斯算子时,所有可能的亲和矩阵上的最大特征值存在一个上限,此时方程为:
\[\mathcal{F}(\boldsymbol{A}, \boldsymbol{Z})=\theta_0\boldsymbol{Z}+\theta_1\boldsymbol{A}\boldsymbol{Z}+ \sum_{k=2}^{K-1} \theta_k \boldsymbol{A}^k \boldsymbol{Z}\]将上式扩展到多个通道:
\[\mathcal{F}(\boldsymbol{A}, \boldsymbol{Z})=\boldsymbol{Z}W_1+\boldsymbol{A}\boldsymbol{Z}W_2+ \sum_{k=2}^{K-1} \boldsymbol{A}^k \boldsymbol{Z}W_{k+1}\]现有的Nonlocal结构都可以从频域角度进行分析:

除了统一现有的Nonlocal结构,提出的“频谱视图”还可以帮助设计具有理论保证的新的基于非局部的块。因为之前的Nonlocal不保证对称性,得出的不是近似的完整形式,因此作者使用对称亲和矩阵,进而设计了谱非局部模块(spectral Nonlocal, SNL)。
\[\boldsymbol{Y}=\boldsymbol{X}+\mathcal{F}_s(\boldsymbol{A}, \boldsymbol{Z})=\boldsymbol{X}+\boldsymbol{Z}W_1+\boldsymbol{A}\boldsymbol{Z}W_2 \\ \text{s.t. } \boldsymbol{A} = \boldsymbol{D}^{-1/2}_{\hat{M}}\hat{M}\boldsymbol{D}^{-1/2}_{\hat{M}},\hat{M}=(M+M^T)/2\]
输入特征图$X$首先被送入三个1×1卷积降低通道数,其中一个输出$Z$用作传递的特征映射,其他两个用来得出亲和矩阵$A$,然后使$A$对称并归一化,利用亲和矩阵$A$和转移的特征映射$Z$获得非局部块的输出。最后恢复通道数再相加。
class SNLUnit(nn.Module):
def __init__(self, inplanes, planes):
super(SNLUnit, self).__init__()
self.g = nn.Conv2d(inplanes, planes, kernel_size=1, stride=1, bias=False)
self.bn = nn.BatchNorm2d(inplanes)
self.w_1 = nn.Conv2d(planes, inplanes, kernel_size=1, stride=1, bias=False)
self.w_2 = nn.Conv2d(planes, inplanes, kernel_size=1, stride=1, bias=False)
def forward(self, x, att):
residual = x
g = self.g(x)
b, c, h, w = g.size()
g = g.view(b, c, -1).permute(0, 2, 1)
x_1 = g.permute(0, 2, 1).contiguous().view(b,c,h,w)
x_1 = self.w_1(x_1)
out = x_1
x_2 = torch.bmm(att, g)
x_2 = x_2.permute(0, 2, 1)
x_2 = x_2.contiguous()
x_2 = x_2.view(b, c, h, w)
x_2 = self.w_2(x_2)
out = out + x_2
out = self.bn(out)
out = torch.relu(out)
out = out + residual
return out


