t-distributed stochastic neighbor embedding。

• paper：Visualizing Data using t-SNE

t分布随机近邻嵌入(t-distributed stochastic neighbor embedding, t-SNE)是一种非线性降维算法，非常适用于高维数据降维到2维或者3维，进行可视化。

t-SNE在高维样本空间中为每个样本点构建一个概率分布，用于拟合样本点之间的相对位置关系；在降维后的低维空间中也为其对应的样本构建一个概率分布，用于拟合降维样本点之间的位置关系。把降维后的样本点看作可学习参数，通过梯度更新使得两个空间中对应的概率分布足够接近。

1. SNE算法

t-SNE算法是对随机近邻嵌入(stochastic neighbor embedding, SNE)算法的改进，因此首先介绍SNE算法。

SNE算法在样本空间中对每个样本点建立一个条件概率分布，对于任意样本点$x_i$，使用高斯分布建模与该样本的距离（通常用Euclidean距离）不同的其余样本点出现的概率：

若指定该样本点对应概率分布的方差 $\sigma_i^2$，则将样本点$x_j$与样本点$x_i$之间的位置关系建模为：

上式中分子用高斯分布衡量两个样本之间的相似性(距离)，分母对概率进行归一化。

对于降维后的低维空间，样本点$x_j$与$x_i$对应的降维样本点$y_j$与$y_i$也应有类似位置关系，采用固定方差的高斯分布建模：

问题转化为使得两个条件概率足够接近，通常使用KL散度衡量这两个分布的距离：

可以通过梯度下降算法对上式进行数值优化，从而获得满足条件的降维样本点。

2. t-SNE的改进

SNE算法存在一些缺陷，t-SNE算法对其进行了改进。 SNE算法的主要缺陷包括：

① 位置关系不对称

SNE算法中构造的样本点之间的位置关系如下：

注意到上述位置关系不是对称的，即$p_{j|i}≠p_{i|j}, q_{j|i}≠q_{i|j}$。

将条件概率修改为联合概率，可以得到对称的位置关系表达式：

在实际应用中计算联合概率比较复杂，因此采用下面的方法构造对称的位置关系：

② 数据分布不同步

在高维的样本空间中，样本之间的相对位置使用高斯分布建模。在低维的空间中，样本分布通常具有长尾(heavy-tailed)特性，因此低维空间中的概率分布改为使用t分布建模。

低维空间中的样本点$y_j$与$y_i$之间的位置关系按照t分布建模为：

通过t分布的修正，在高维空间中距离较近的两点映射到低维空间后距离会更近；在高维空间中距离较远的两点映射到低维空间后距离会更远。 t分布相对于高斯分布，对离群点(outlier)不敏感：

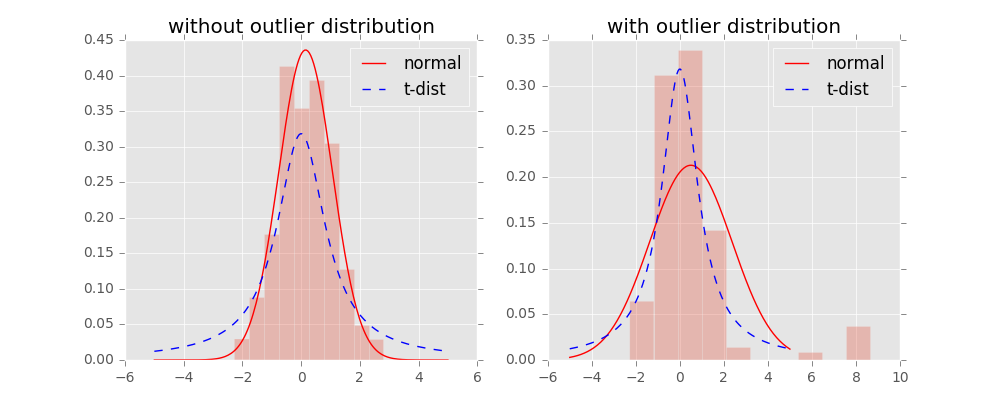
③ 方差$\sigma_i^2$的设置

在高维空间中，样本点$x_i$处构造的概率分布的方差$\sigma_i^2$相当于设置了软性的阈值，决定了其余样本点对该样本点的“有效性”。比如对于通常的高斯分布，可以认为距离分布在$3\sigma$区间内的样本点与中心样本点相似度较高，这些点在计算中起主要作用。

t-SNE在选择$\sigma_i^2$时采用了随机近邻(stochastic neighbor)的设置，即当样本点$x_i$附近的样本点较多时，采用较小的$\sigma_i^2$；当样本点$x_i$附近的样本点较少时，采用较大的$\sigma_i^2$。

具体地，每个样本$x_i$的方差$\sigma_i^2$是使用困惑度(perplexity)进行选择的。困惑度与概率分布的熵呈指数相关：

较低的困惑度意味着在匹配原分布并拟合每一个数据点到目标分布时只考虑最近的几个最近邻点，而较高的困惑度意味着拥有较大的全局观。

由于高维空间中的样本点$x_j$与样本点$x_i$是已知的，因此预先给定困惑度的值(常取5-50)，则可确定方差$\sigma_i^2$，查找过程可以采用二分法。

在实际中记$\beta_i=\frac{1}{2\sigma_i^2}$，通过指定困惑度寻找合适的$\beta_i$。

3. t-SNE的流程

由上述介绍，t-SNE的一般步骤如下：

1. 给定输入样本$X \in \Bbb{R}^{N \times d}$和降维维度$d’$;
2. 对于每个样本点$x_i$，计算其余样本点的条件概率$p_{j|i} = \frac{\exp( -|| x_i -x_j ||^2 /2σ_i^2 )}{\sum_{k≠i}^{} {\exp( -|| x_k -x_i ||^2 /2σ_i^2 )}}$；
3. 进一步计算联合概率$p_{ij} = p_{i|j}+p_{j|i},p_{ij} = \frac{p_{ij}}{\sum_{i}^{} \sum_{j}^{} p_{ij}}$；
4. 随机生成低维样本$Y \in \Bbb{R}^{N \times d’}$；
5. 计算低维样本的联合概率$q_{ij} = \frac{ (1 + || y_i-y_j ||^2)^{-1} }{\sum_{k≠l}^{} {(1 + || y_k-y_l ||^2 )^{-1} }}$；
6. 计算两个概率的KL散度$\sum_{i}^{} \sum_{j}^{} p_{ij} \log (\frac{p_{ij}}{q_{ij}})$；
7. 使用梯度法更新低维样本$Y$。

梯度更新公式如下：

t-SNE算法也存在一些缺陷。由于t-SNE倾向于保留数据中的局部特征，对于本征维数(intrinsic dimensionality)本身就很高的数据集，是不可能完整的映射到2或3维的空间； t-SNE主要用于可视化，没有显式的预估部分，很难用于其他目的（比如预处理）。

4. 代码实现

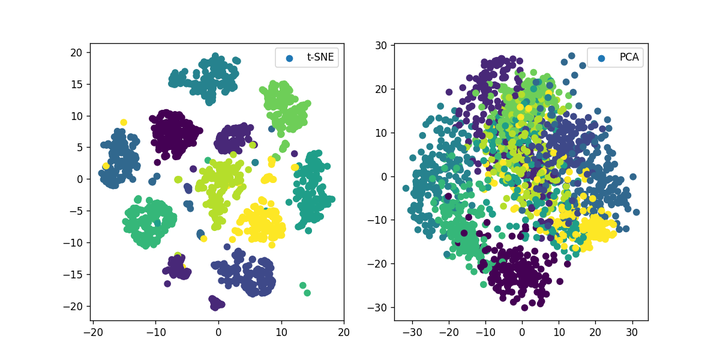
实例：使用PCA和t-SNE对手写数字数据集降维可视化

①导入相关的库：

from sklearn.datasets import load_digits
from sklearn.manifold import TSNE
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

②使用PCA和t-SNE降维：

digits = load_digits()
X_tsne = TSNE(n_components=2,random_state=33).fit_transform(digits.data)
X_pca = PCA(n_components=2).fit_transform(digits.data)

③可视化：

plt.figure(figsize=(10, 5))
plt.subplot(121)
plt.scatter(X_tsne[:, 0], X_tsne[:, 1], c=digits.target,label="t-SNE")
plt.legend()
plt.subplot(122)
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=digits.target,label="PCA")
plt.legend()
plt.show()