Multi Task Learning.

本文目录：

  1. 多任务学习的定义及特点
  2. 多任务学习的网络结构
  3. 多任务学习的损失函数

1. 多任务学习的定义及特点

多任务学习(multi-task learning, MTL)是指同时学习多个属于不同领域(domain)的任务，并通过特定任务的领域信息提高泛化能力。

MTL improves generalization by leveraging the domain-specific information contained in the training signals of related tasks.

多任务学习的特点如下：

通常MTL处理的任务应具有一定的关联性。若同时学习两个不相关甚至有冲突的任务，可能会损害模型的表现，这个现象称为negative transfer。

与标准的单任务学习相比，多任务学习的方法设计可以分别从网络结构与损失函数两个角度出发。

2. 多任务学习的网络结构

一个高效的多任务网络，应同时兼顾特征共享部分和任务特定部分，既需要学习任务之间的泛化表示(避免过拟合)，又需要学习每个任务独有的特征(避免欠拟合)。

根据模型在处理不同任务时网络参数的共享程度，MTL方法的网络结构可分为：

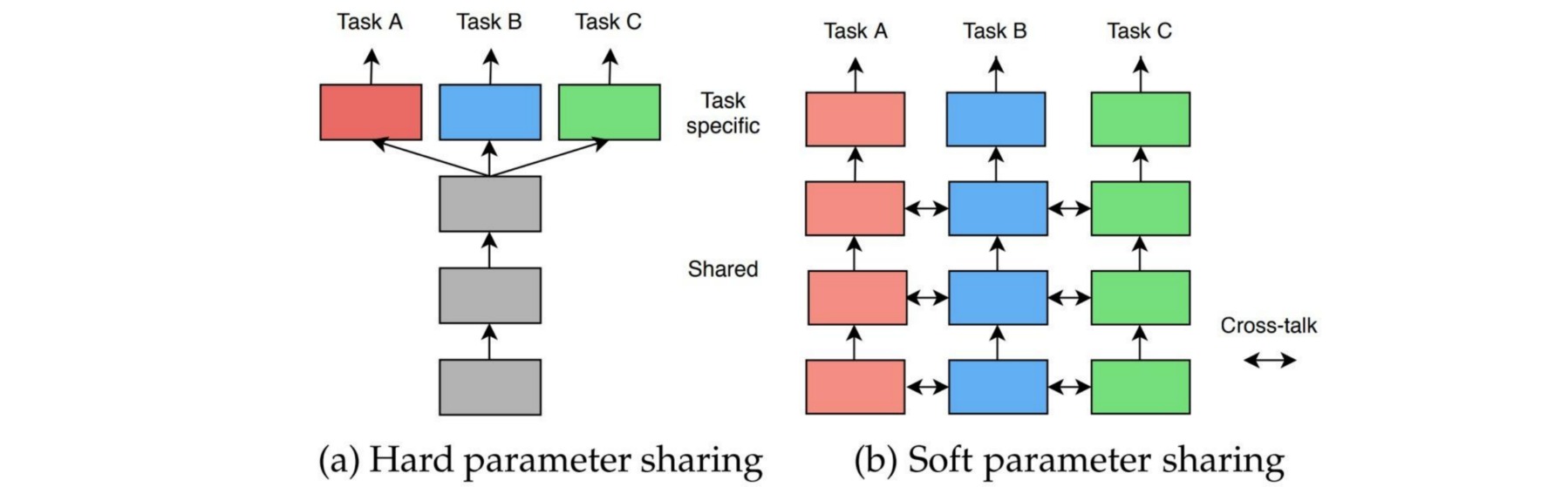
(1) 硬参数共享 Hard Parameter Sharing

Hard Parameter Sharing是指模型在处理不同任务时，其主体部分共享参数，针对不同任务使用不同的输出结构。这类方法通过在不同任务上学习共享的特征，降低模型在单个任务上过拟合的风险。

⚪ Multilinear Relationship Network：使用张量正态先验约束输出结构

⚪ Fully-adaptive Feature Sharing：通过全自适应特征共享逐层加宽网络

(2) 软参数共享 Soft Parameter Sharing

Soft Parameter Sharing是指针对每个任务使用具有独立参数的模型，对不同任务的模型参数进行额外的距离约束。这类方法通常能够在单个任务上实现更好的表现，但模型参数与任务数量呈倍数增长。

⚪ Cross-Stitch Network：使用线性组合构造特征图

⚪ Sluice Network：使用线性组合构造层次化特征图

⚪ Multi-Task Attention Network：使用注意力机制设置构造特征图

3. 多任务学习的损失函数

多任务学习将多个相关的任务共同训练，其总损失函数是每个任务的损失函数的加权求和式：\(\mathcal{L}_{total} = \sum_{k}^{} w_k\mathcal{L}_k\)。权重的选择应能够平衡每个任务的训练，使得各任务都获得有益的提升。

(1) 如何设置权重：帕累托最优

多任务学习的目的是寻找模型的最优参数$\theta^{*}$。若该参数任意变化都会导致某个任务$k$的损失函数\(\mathcal{L}_k\)增大，则称$\theta^{*}$为帕累托最优解(Pareto Optimality)。帕累托最优意味着每个任务的损失都比较小，不能通过牺牲某个任务来换取另一个任务的性能提升。

若参数的更新过程采用梯度下降法，则多任务学习的主要工作是寻找一个尽可能与每个任务的梯度\(\nabla_{\theta} \mathcal{L}_k\)都相反的方向作为更新方向，等价于构造向量$u$使得参数更新方向为$\Delta \theta = -\eta u$。构造最优化问题：

\[\forall k, \langle \nabla_{\theta} \mathcal{L}_k,u \rangle \geq 0 \Leftrightarrow \mathop{\min}_{k} \langle \nabla_{\theta} \mathcal{L}_k,u \rangle \geq 0 \Leftrightarrow \mathop{\max}_{u} \mathop{\min}_{k} \langle \nabla_{\theta} \mathcal{L}_k,u \rangle\]

若定义\(\Bbb{P}^K\)为所有$K$元离散分布的集合：

\[\Bbb{P}^K = \{ (w_1,w_2,\cdots,w_K) | w_1,w_2,\cdots,w_K\geq 0,\sum_{k} w_k = 1 \}\]

则优化目标等价于：

\[\mathop{\min}_{k} \langle \nabla_{\theta} \mathcal{L}_k,u \rangle = \mathop{\min}_{w \in \Bbb{P}^K} \langle \sum_k w_k\nabla_{\theta} \mathcal{L}_k,u \rangle = \mathop{\min}_{w \in \Bbb{P}^K} \langle \sum_k \nabla_{\theta} w_k\mathcal{L}_k,u \rangle\]

因此通过为损失函数\(\mathcal{L}_k\)设置合适的权重$w_k$，使得上述目标取得最小值，并进一步选择使得该最小值最大的向量$u$，便可以构造使目标逐渐接近帕累托最优的参数更新方向。

本节首先介绍一些权重的手动设置方法，并讨论它们的特点；下一节将介绍一些自动设置权重的方法。

⚪ 根据初始状态设置权重

在没有任何任务先验的情况下，总损失可以设置为所有任务损失的算术平均值，即$w_k=1/K$。然而每个任务的损失函数的数量级和物理量纲都不同，因此可以使用损失函数初始值的倒数进行无量纲化：

\[w_k = \frac{1}{\mathcal{L}_k^{(0)}}\]

该权重具有缩放不变性，即任务$k$的损失大小进行缩放后结果不会变化。

损失函数初始值既可以取前几次批量的损失平均估计，也可以基于任务假设得到理论值。比如假设模型的初始输出是零向量，则$C$分类任务的初始损失为$-\log \frac{1}{C}=\log C$；而回归任务的初始损失为$\Bbb{E}_y[||y-0||^2]=\Bbb{E}_y[||y||^2]$。

⚪ 根据先验状态设置权重

若能够预先获取数据集的标签信息，则可以根据其统计值构造损失函数的先验状态\(\mathcal{L}_k^{\text{prior}}\)，并用作权重：

\[w_k = \frac{1}{\mathcal{L}_k^{\text{prior}}}\]

先验状态可以代表当前任务的初始难度。比如$C$分类任务中统计每个类别的出现频率为$[p_1,\cdots,p_K]$，则先验状态\(\mathcal{L}_k^{\text{prior}}=-\sum_{k}^{K}p_k\log p_k\)；而回归任务的中统计所有样本标签的期望\(\mu = \Bbb{E}_y[y]\)，则先验状态\(\mathcal{L}_k^{\text{prior}}=\Bbb{E}_y[\|y-\mu\|^2]\)。

⚪ 根据实时状态设置权重

根据初始状态和先验状态设定的权重都是固定值，更合理的方案是根据训练过程中的实时状态动态地调整权重：

\[w_k^{(t)} = \frac{1}{sg(\mathcal{L}_k^{(t)})}\]

其中$sg(\cdot)$表示stop gradient，即在反向传播时不计算其梯度，在pytorch中可以通过.detach()方法实现。在该权重设置下，虽然每个任务的损失函数恒为$1$，但梯度不恒为$0$；对应的总损失函数梯度表示为：

\[\begin{aligned} \nabla_{\theta} \mathcal{L}_{total} &= \nabla_{\theta} \sum_k^K \frac{\mathcal{L}_k}{sg(\mathcal{L}_k^{(t)})} = \sum_k^K \nabla_{\theta} \frac{\mathcal{L}_k}{sg(\mathcal{L}_k^{(t)})} = \sum_k^K \frac{\nabla_{\theta} \mathcal{L}_k}{\mathcal{L}_k^{(t)}} \\ &= \sum_k^K \nabla_{\theta} \log \mathcal{L}_k = \nabla_{\theta} \log \prod_k^K \mathcal{L}_k = \nabla_{\theta} K\log \sqrt[K]{\prod_k^K \mathcal{L}_k} \end{aligned}\]

此时总损失函数等价于每个任务的损失函数的几何平均值。

⚪ 根据梯度状态设置权重

上述几种权重设置都具有缩放不变性；却不具有平移不变性，即任务$k$的损失加上一个常数后结果会发生变化。因此考虑采用损失函数梯度的模长来代替损失本身，以构造权重：

\[w_k^{(t)} = \frac{1}{sg(||\nabla_{\theta} \mathcal{L}_k^{(t)}||)}\]

该权重同时具有缩放与平移不变性。此时总损失函数的梯度表示为：

\[\nabla_{\theta} \mathcal{L}_{total} = \nabla_{\theta} \sum_k^K \frac{\mathcal{L}_k}{sg(||\nabla_{\theta} \mathcal{L}_k^{(t)}||)} = \sum_k^K \frac{\nabla_{\theta} \mathcal{L}_k}{sg(||\nabla_{\theta} \mathcal{L}_k^{(t)}||)}\]

因此该权重设置等价于将每个任务损失的梯度进行归一化后，再把梯度累加起来参与梯度更新。

(2) 权重的自动设置

多任务学习的损失函数形式为\(\mathcal{L}_{total} = \sum_{k}^{} w_k\mathcal{L}_k\)，对每个任务的损失进行权重分配。如何自动进行权重选择，避免网络过于关注某任务是十分重要的。下面介绍一些权重自动选择方法：

方法 权重 辅助参数
Uncertainty：根据同方差不确定度设置权重 \(\sum_{k=1}^{K}\frac{1}{2\sigma_k^2}\mathcal{L}_k(\theta)+\log \sigma_k\) -
Gradient Normalization：根据梯度量级和训练速度更新权重 \(w_k^{(t+1)} \gets w_k^{(t)}-\lambda \nabla_{w_k}\mathcal{L}_{\text{grad}}\) \(\begin{aligned} \mathcal{L}_{\text{grad}}(t;w_k^{(t)}) &= \sum_{k=1}^{K} | G_k^{(t)}-\overline{G}^{(t)} \times [r_k^{(t)}]^{\alpha} |_1 \\ G_k^{(t)} = || & \nabla_{\theta}w_k^{(t)}\mathcal{L}_k||_2 ,\overline{G}^{(t)} = \Bbb{E}_k[ G_k^{(t)}] \\ r_k^{(t)} &= \frac{\mathcal{L}_k^{(t)}/\mathcal{L}_k^{(0)}}{\Bbb{E}_k[\mathcal{L}_k^{(t)}/\mathcal{L}_k^{(0)}]} \end{aligned}\)
Dynamic Weight Average：根据损失相对下降率设置权重 \(w_k^{(t)} = \frac{K \exp(r_k^{(t-1)}/T)}{\sum_{i}^{}\exp(r_i^{(t-1)}/T)}\) \(r_k^{(t-1)}=\frac{\mathcal{L}_k^{(t-1)}}{\mathcal{L}_k^{(t-2)}}\)
Multi-Objective Optimization：通过Frank-Wolfe算法求帕累托最优解 \(w_k^{(t+1)} = (1-\gamma)w_k^{(t)}+\gamma e_{\tau}\) \(\begin{aligned} \tau &= \mathop{\arg \min}_k \langle \nabla_{\theta} \mathcal{L}_k,\sum_k w_k^{(t)}\mathcal{L}_k \rangle \\ \gamma &= \mathop{\arg \min}_{\gamma} \sum_k((1-\gamma)w_k^{(t)}+\gamma e_{\tau} )\mathcal{L}_k \end{aligned}\)
Dynamic Task Prioritization：根据动态任务优先级设置权重 \(w_k^{(t)} = -(1-\overline{\kappa}_k^{(t)})^{\gamma_t} \log(\overline{\kappa}_k^{(t)})\) \(\overline{\kappa}_k^{(t)} = \alpha * \kappa_k^{(t)} + (1-\alpha) * \overline{\kappa}_k^{(t-1)}\)
Loss-Balanced Task Weighting：根据损失变化设置权重 \(w_k^{(t)} = (\frac{\mathcal{L}_k^{(t)}}{\mathcal{L}_k^{(0)}})^{\alpha}\) -

⚪ 参考文献