使用卷积神经网络实现数值坐标回归.
在人体姿态估计任务中,常见的关键点坐标预测有两种:
- 采用全连接层直接回归坐标点。该类做法的优点是输出即为坐标点,训练和前向速度可以很快,且是端到端的全微分训练;缺点是缺乏空间泛化能力,丢失了特征图上面的空间信息,容易过拟合。
- 采用预测高斯热图方式,然后argmax找出峰值对应的索引即为坐标点。该类做法优点是精度通常较高;缺点是不是一个全微分的模型,并且由于其要求的输出特征图很大,训练和前向速度很慢,且内存消耗大。

本文设计了一个differentiable spatial to numerical transform(DSTN)模块来弥补两者不足,并且设计的模块是没有训练参数的,可以在低分辨率高斯图上预测,主要作用就是让梯度流可以从坐标点流到高斯热图上,而不增加额外参数和计算量。

假设CNN原图输入是$(h,w,3)$,输出是$(h/4,w/4,17)$表示$17$个关键点热图,用$Z$表示;DSNT作用在每一个通道上,输出是$(17,2)$表示$17$个关键点的$x,y$坐标。
首先对每一个通道输出的高斯热图进行归一化,作者选择不同的归一化手段,最终选择了softmax作为归一化函数。

定义两个矩阵$X$和$Y$,其宽高和输入DSNT的宽高一致,其具体数值计算为:
\[X_{i,j} = \frac{2j-(n+1)}{n},Y_{i,j} = \frac{2i-(m+1)}{m}\]这样可以将$X$和$Y$坐标值归一化到$(-1,1)$之间。最终的$x$坐标是$Z$和$X$矩阵进行$F$范数结果(逐元素点乘),$y$坐标是$Z$和$Y$矩阵进行$F$范数结果。
\[DSTN(\hat{Z}) = \left[ \langle \hat{Z},X\rangle_F, \langle\hat{Z},Y\rangle_F\right]\]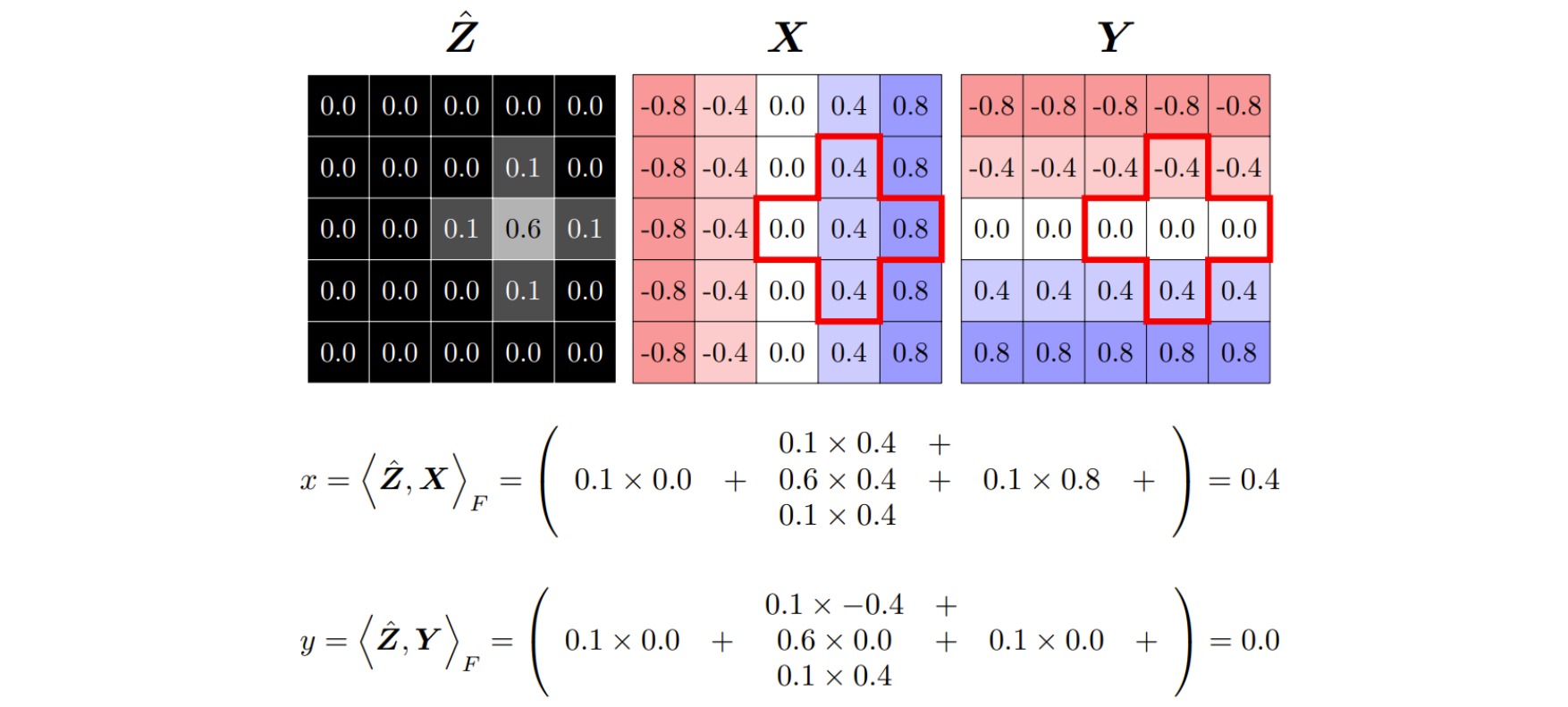
损失函数包括坐标点的平方误差损失和热图的正则损失:
\[\begin{aligned} &\mathcal{L}(\hat{Z}, p)=\mathcal{L}_{\text {euc }}(\operatorname{DSNT}(\hat{Z}), p)+\lambda \mathcal{L}_{\text {reg }}(\hat{Z})\\ \end{aligned}\]其中平方误差损失用于坐标点回归:
\[\begin{aligned} &\mathcal{L}_{\text {euc }}(\boldsymbol{\mu}, \boldsymbol{p})=\|\boldsymbol{p}-\boldsymbol{\mu}\|_2\\ \end{aligned}\]热图正则损失用于约束中间热图与高斯热图接近。既可以直接约束热图方差:
\[\begin{aligned} & \operatorname{Var}\left[c_x\right]=\mathbb{E}\left[\left(c_x-\mathbb{E}\left[c_x\right]\right)^2\right] =\left\langle\hat{Z},\left(\boldsymbol{X}-\mu_x\right) \odot\left(\boldsymbol{X}-\mu_x\right)\right\rangle_F \\ & \mathcal{L}_{\text {var }}(\hat{Z})=\left(\operatorname{Var}\left[\mathrm{c}_x\right]-\sigma_t^2\right)^2+\left(\operatorname{Var}\left[\mathrm{c}_y\right]-\sigma_t^2\right)^2 \\ \end{aligned}\]也可以约束两种分布的散度:
\[\begin{aligned} &\mathcal{L}_D(\hat{Z}, \boldsymbol{p})=D\left(p(\mathbf{c}) \| \mathcal{N}\left(\boldsymbol{p}, \sigma_t^2 \boldsymbol{I}_2\right)\right) \end{aligned}\]实验结果表明,使用JS分布正则的效果最好:



