用于人体姿态估计的堆叠沙漏网络.
本文提出了堆叠沙漏网络(Stacked Hourglass Network)用于人体姿态估计,该网络结构能够捕获并整合图像不同尺度的信息。堆叠沙漏网络是由若干个Hourglass模块堆叠而成,长得很像堆叠起来的沙漏:

Hourglass模块结构是对称的,包含重复的降采样(高分辨率到低分辨率,由最大池化实现)和上采样(低分辨率到高分辨率,由最近邻插值实现),此外还使用了残差连接保存不同分辨率下的空间信息。

与DeepPose采用级联回归器目的相似,Hourglass模块可以捕捉利用多个尺度上的信息,例如局部特征信息对于识别脸部、手部等特征十分重要,但人体最终的姿态估计也需要图像的全局特征信息。
直接对人体的$k$对关键点坐标进行回归比较困难,因此Hourglass将回归问题转换为预测$k$个关键点的热图heatmap,其中第$i$个热图表示第$i$个关键点的位置置信度分布,用于预测每个像素点是关键点的概率。Ground Truth热图构造为以实际关节点位置为中心的标准正态分布,采用均方误差损失。

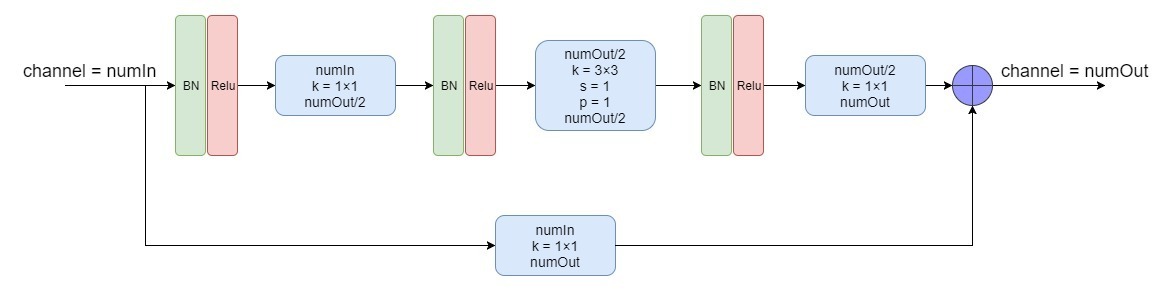
在Hourglass模块中,基本的卷积层是由如下残差模块定义的:
class BnReluConv(nn.Module):
def __init__(self, inChannels, outChannels, kernelSize = 1, stride = 1, padding = 0):
super(BnReluConv, self).__init__()
self.bn = nn.BatchNorm2d(inChannels)
self.conv = nn.Conv2d(inChannels, outChannels, kernelSize, stride, padding)
self.relu = nn.ReLU()
def forward(self, x):
x = self.bn(x)
x = self.relu(x)
x = self.conv(x)
return x
class ConvBlock(nn.Module):
def __init__(self, inChannels, outChannels):
super(ConvBlock, self).__init__()
self.cbr1 = BnReluConv(inChannels, outChannels//2 1, 1, 0)
self.cbr2 = BnReluConv(outChannels//2, outChannels//2, 3, 1, 1)
self.cbr3 = BnReluConv(outChannels//2, outChannels, 1, 1, 0)
def forward(self, x):
x = self.cbr1(x)
x = self.cbr2(x)
x = self.cbr3(x)
return x
class SkipLayer(nn.Module):
def __init__(self, inChannels, outChannels):
super(SkipLayer, self).__init__()
if (inChannels == outChannels):
self.conv = None
else:
self.conv = nn.Conv2d(inChannels, outChannels, 1)
def forward(self, x):
if self.conv is not None:
x = self.conv(x)
return x
class Residual(nn.Module):
def __init__(self, inChannels, outChannels):
super(Residual, self).__init__()
self.inChannels = inChannels
self.outChannels = outChannels
self.cb = ConvBlock(inChannels, outChannels)
self.skip = SkipLayer(inChannels, outChannels)
def forward(self, x):
out = self.cb(x)
out = out + self.skip(x)
return out
Hourglass模块由上述残差块递归地构成。定义一个阶数来表示递归的层数,一阶的Hourglass模块如下:

多阶的Hourglass模块是将上图虚线框中的块递归地替换为一阶Hourglass模块,作者在实验中使用的是4阶的HHourglass模块:

class Hourglass(nn.Module):
def __init__(self, nChannels = 256, numReductions = 4, nModules = 2, poolKernel = (2,2), poolStride = (2,2), upSampleKernel = 2):
super(Hourglass, self).__init__()
_skip = []
for _ in range(nModules):
_skip.append(Residual(nChannels, nChannels))
self.skip = nn.Sequential(*_skip)
self.mp = nn.MaxPool2d(poolKernel, poolStride)
_afterpool = []
for _ in range(nModules):
_afterpool.append(Residual(nChannels, nChannels))
self.afterpool = nn.Sequential(*_afterpool)
if (numReductions > 1):
self.hg = Hourglass(nChannels, numReductions-1, nModules, poolKernel, poolStride)
else:
_num1res = []
for _ in range(nModules):
_num1res.append(Residual(nChannels,nChannels))
self.num1res = nn.Sequential(*_num1res)
_lowres = []
for _ in range(nModules):
_lowres.append(Residual(nChannels,nChannels))
self.lowres = nn.Sequential(*_lowres)
self.up = nn.Upsample(scale_factor = upSampleKernel)
def forward(self, x):
out1 = x
out1 = self.skip(out1)
out2 = x
out2 = self.mp(out2)
out2 = self.afterpool(out2)
if self.numReductions > 1:
out2 = self.hg(out2)
else:
out2 = self.num1res(out2)
out2 = self.lowres(out2)
out2 = self.up(out2)
return out2 + out1
堆叠沙漏网络的整体结构是由若干个Hourglass模块堆叠而成,从而使得网络能够不断重复自底向上和自顶向下的过程。网络输入的图片分辨率为256×256,在hourglass模块中的最大分辨率为64×64,整个网络最开始要经过一个7×7的步长为2的卷积层,之后再经过一个残差块和最大池化层使得分辨率从256降到64。
作者在堆叠沙漏网络的每个Hourglass模块后引入了中间监督来对每一个Hourglass模块进行预测,即对中间层的heatmaps计算损失。通过引入中间监督,使得网络在早期就能进行预测,即整个网络的一部分也能够对图片有一个高层次的理解(中间监督设计在如下图所示位置)。

在整个网络中,作者共使用了8个hourglass模块,并且所有的模块都基于相同的ground truth添加了损失函数。

class StackedHourGlass(nn.Module):
def __init__(self, nChannels, nStack, nModules, numReductions, nJoints):
super(StackedHourGlass, self).__init__()
self.start = BnReluConv(3, 64, kernelSize = 7, stride = 2, padding = 3)
self.res1 = Residual(64, 128)
self.mp = nn.MaxPool2d(2, 2)
self.res2 = Residual(128, 128)
self.res3 = Residual(128, nChannels)
_hourglass, _Residual, _lin1, _chantojoints, _lin2, _jointstochan = [],[],[],[],[],[]
for _ in range(self.nStack):
_hourglass.append(Hourglass(nChannels, numReductions, nModules))
_ResidualModules = []
for _ in range(nModules):
_ResidualModules.append(Residual(nChannels, nChannels))
_ResidualModules = nn.Sequential(*_ResidualModules)
_Residual.append(_ResidualModules)
_lin1.append(BnReluConv(nChannels, nChannels))
_chantojoints.append(nn.Conv2d(nChannels, nJoints, 1))
_lin2.append(nn.Conv2d(nChannels, nChannels, 1))
_jointstochan.append(nn.Conv2d(nJoints, nChannels, 1))
self.hourglass = nn.ModuleList(_hourglass)
self.Residual = nn.ModuleList(_Residual)
self.lin1 = nn.ModuleList(_lin1)
self.chantojoints = nn.ModuleList(_chantojoints)
self.lin2 = nn.ModuleList(_lin2)
self.jointstochan = nn.ModuleList(_jointstochan)
def forward(self, x):
x = self.start(x)
x = self.res1(x)
x = self.mp(x)
x = self.res2(x)
x = self.res3(x)
out = []
for i in range(self.nStack):
x1 = self.hourglass[i](x)
x1 = self.Residual[i](x1)
x1 = self.lin1[i](x1)
out.append(self.chantojoints[i](x1))
x1 = self.lin2[i](x1)
x = x + x1 + self.jointstochan[i](out[i])
return (out)
作者对中间监督的位置进行消融实验,结果最好的是HG-Int,即在最终输出分辨率之前的两个最高分辨率上进行上采样后应用中间监督。

作者也对hourglass模块的堆叠个数进行消融实验:



