ON-LSTM:把树结构整合进循环神经网络.
本文作者设计了ON-LSTM,通过有序神经元(Ordered Neuron)把层级结构(树结构)整合到LSTM中,从而允许LSTM能自动学习到层级结构信息;不仅提高了语言模型的效果,还可以无监督地学习到句子的句法结构。
1. LSTM与层级结构
LSTM网络引入了输入门$i$ (input gate)、遗忘门$f$ (forget gate),和输出门$o$ (output gate);并把输入和隐状态整合为记忆状态$c$(cell state);根据遗忘门和输入门更新记忆状态后,根据输出门更新隐状态。
\[\begin{aligned} i_t &= \sigma(W_{i}x_t+U_{i}h_{t-1}+b_i) \\ f_t &= \sigma(W_{f}x_t+U_{f}h_{t-1}+b_f) \\ o_t &= \sigma(W_{o}x_t+U_{o}h_{t-1}+b_o) \\ \hat{c}_t &= \text{tanh}(W_{c}x_t+U_{c}h_{t-1}+b_c) \\ c_t &= f_t \odot c_{t-1} + i_t \odot \hat{c}_t \\ h_{t} &= o_t \odot \text{tanh}(c_t) \end{aligned}\]
LSTM的神经元是无序的,比如遗忘门$f_t$是一个向量,如果把LSTM运算过程中涉及到的所有向量的位置按照同一方式重新打乱,并相应地打乱权重的顺序,则输出结果只是原向量的重新排序,信息量不变。
一个自然语义句子通常能表示为一些层级结构,这些结构能够抽象为句法信息。层级越低代表语言中颗粒度越小的结构,而层级越高则代表颗粒度越粗的结构,比如在中文句子中,“字”可以认为是最低层级的结构,然后依次是词、词组、短语等。层级越高,颗粒度越粗,那么它在句子中的跨度就越大。
ON-LSTM希望能够模型在训练的过程中自然地学习到这种层级结构,实现过程是把记忆状态神经元$c_t$排序,用于表示一些特定的结构,从而用神经元的序信息表示层级结构。

2. ON-LSTM的更新过程
ON-LSTM在编码时能区分高低层级的信息;高层级的信息对应的编码区间保留更久,而低层级的信息在对应的区间更容易被遗忘。
假设ON-LSTM中的神经元$c_t$都排好序,$c_t$中索引值越小的元素表示越低层级的信息,而索引值越大的元素表示越高层级的信息。
ON-LSTM在每个时刻把输入和隐状态整合为记忆状态的方式与LSTM相同:
\[\begin{aligned} \hat{c}_t &= \text{tanh}(W_{c}x_t+U_{c}h_{t-1}+b_c) \end{aligned}\]每次在更新$c_t$之前,首先预测两个整数$d_f$和$d_i$,分别表示历史信息$h_{t−1}$和当前输入$x_t$的层级。
若$d_f<d_i$,表明当前输入$x_t$的层级要高于历史信息$h_{t−1}$的层级,因此把当前输入信息整合到$[d_f,d_i]$的层级中:
\[c_t = \begin{pmatrix} \hat{c}_{t,<d_f} \\ f_{t,[d_f,d_i]} \odot c_{t-1,[d_f,d_i]} + i_{t,[d_f,d_i]} \odot \hat{c}_{t,[d_f,d_i]} \\ c_{t-1,>d_i} \end{pmatrix}\]对于当前输入\(\hat{c}_t\),更容易影响低层信息,所以当前输入影响的范围是$[0,d_i]$;对于历史信息$c_{t−1}$,保留的是高层信息,所以影响的范围是$[d_f,d_{\max}]$;在重叠部分$[d_f,d_i]$,通过LSTM的形式更新记忆状态。
若$d_f>d_i$,表明当前输入$x_t$的层级和历史信息$h_{t−1}$的层级没有重叠,因此$(d_i,d_f)$区间保持初始状态(全零):
\[c_t = \begin{pmatrix} \hat{c}_{t,\leq d_i} \\ 0_{(d_i,d_f)} \\ c_{t-1,\geq d_f} \end{pmatrix}\]ON-LSTM将神经元排序之后,通过位置的前后来表示信息层级的高低,然后在更新神经元时,先分别预测历史的层级$d_f$和输入的层级$d_i$,通过这两个层级来对神经元实行分区间更新。
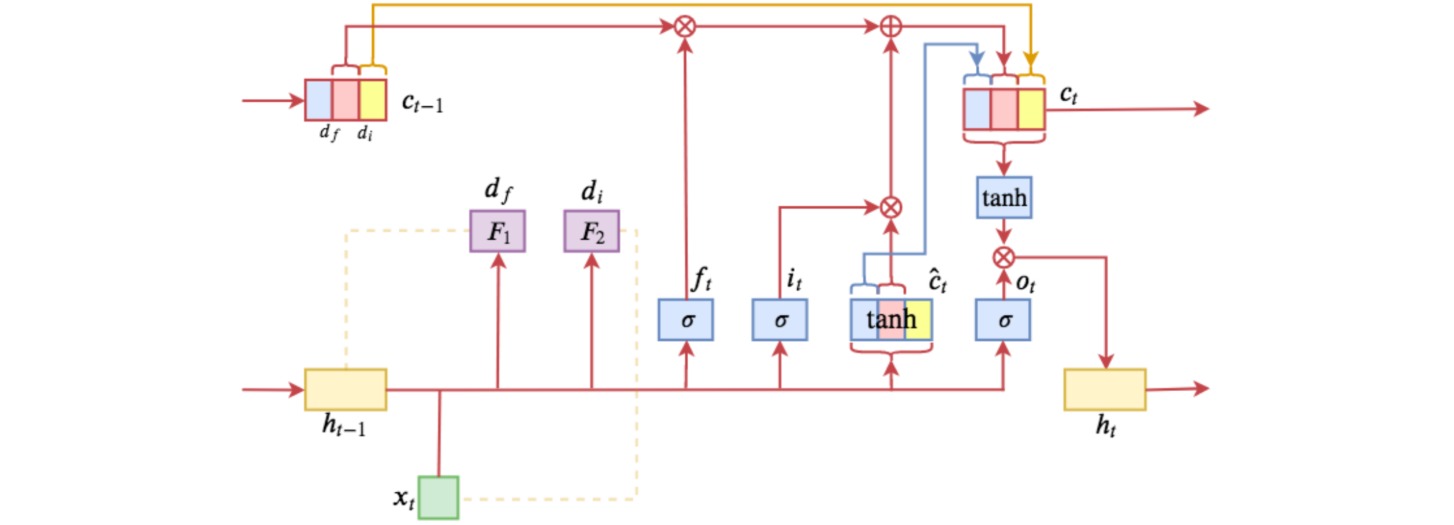
ON-LSTM的分区间更新如图所示。图中上方$c_{t-1}$为历史信息,黄色部分为历史信息层级;下方$\hat{c}_t$为当前输入,绿色部分为输入信息层级;中间$c_t$为当前整合的输出,黄色是直接复制的历史信息,绿色是直接复制的输入信息,紫色是按照LSTM方式融合的交集信息,白色是互不相关的全零状态。

基于这种更新方式,高层信息就可能保留相当长的距离(高层直接复制历史信息,导致历史信息可能不断被复制而不改变);而低层信息在每一步输入时都可能被更新(低层直接复制输入,而输入是不断改变的)。通过信息分级嵌入了层级结构:分组更新时更高的组信息传得更远(跨度更大),更低的组信息跨度更小,这些不同的跨度就形成了输入序列的层级结构。
引入记号$1_k$,表示第$k$位为$1$的one-hot向量,则可把$d_f<d_i$和$d_f>d_i$两种情况下的$c_t$更新公式合并。定义cumsum操作:
\[\text{cumsum}([x_1,x_2,\cdots x_n]) =[x_1,x_1+x_2,\cdots, x_1+x_2+\cdots +x_n]\]则定义\(\tilde{f}_t\)用于标记$c_{t-1}$中的历史信息层级,称为主遗忘门(master forget gate):
\[\tilde{f}_t = \text{cumsum}(1_{d_f})\]并定义\(\tilde{i}_t\)用于标记\(\hat{c}_t\)中的输入信息层级,称为主输入门(master input gate):
\[\tilde{i}_t = 1- \text{cumsum}(1_{d_i})\]两个层级的交集$w_t$计算为:
\[w_t = \tilde{f}_t \odot \tilde{i}_t\]则$c_t$更新公式统一写做:
\[c_t = w_t\odot (f_t \odot c_{t-1} + i_t \odot \hat{c}_t) + (\tilde{f}_t-w_t) \cdot c_{t-1} + (\tilde{i}_t-w_t) \cdot \hat{c}_t\]one-hot向量\(1_{d_f}\)和\(1_{d_i}\)的构造过程是不可导的,根据函数的光滑化结论,one-hot向量的光滑近似函数为softmax函数,则\(1_{d_f}\)和\(1_{d_i}\)构造为:
\[\begin{aligned} 1_{d_f} &≈ \text{softmax}(W_{\tilde{f}}x_t+U_{\tilde{f}}h_{t-1}+b_{\tilde{f}}) \\ 1_{d_i} &≈ \text{softmax}(W_{\tilde{i}}x_t+U_{\tilde{i}}h_{t-1}+b_{\tilde{i}}) \end{aligned}\]至此,ON-LSTM的完整更新过程为:
\[\begin{aligned} i_t &= \sigma(W_{i}x_t+U_{i}h_{t-1}+b_i) \\ f_t &= \sigma(W_{f}x_t+U_{f}h_{t-1}+b_f) \\ o_t &= \sigma(W_{o}x_t+U_{o}h_{t-1}+b_o) \\ \hat{c}_t &= \text{tanh}(W_{c}x_t+U_{c}h_{t-1}+b_c) \\ \tilde{f}_t &= \text{cumsum}(\text{softmax}(W_{\tilde{f}}x_t+U_{\tilde{f}}h_{t-1}+b_{\tilde{f}})) \\ \tilde{i}_t &= 1- \text{cumsum}(\text{softmax}(W_{\tilde{i}}x_t+U_{\tilde{i}}h_{t-1}+b_{\tilde{i}})) \\ w_t &= \tilde{f}_t \odot \tilde{i}_t \\ c_t &= w_t\odot (f_t \odot c_{t-1} + i_t \odot \hat{c}_t) + (\tilde{f}_t-w_t) \cdot c_{t-1} + (\tilde{i}_t-w_t) \cdot \hat{c}_t \\ h_{t} &= o_t \odot \text{tanh}(c_t) \end{aligned}\]
3. 实验分析
主遗忘门\(\tilde{f}_t\)和主输入门\(\tilde{i}_t\)分别代表$c_{t-1}$中的历史信息层级和\(\hat{c}_t\)中的输入信息层级,而序列的层级结构的总层级数一般不会太大,因此这两个向量的长度不应该太大。但是这两个向量需要与$f_t$等做逐元素点乘,而LSTM中神经元的特征维度通常比较大。为了解决这个矛盾,把隐层神经元数目$n$分解为$n=pq$,然后构造具有$p$个神经元的\(\tilde{f}_t,\tilde{i}_t\),再把其中的每个神经元重复$q$次。这样既减少了层级的总数,同时还减少了模型的参数量。
作者汇报了语言模型、句法评价、逻辑推理等任务上的性能表现:

ON-LSTM能够无监督地从训练好的模型(比如语言模型)中提取输入序列的层级树结构。提取的思路如下:
历史信息的层级向量\(1_{d_f}\)构造为:
\[\begin{aligned} 1_{d_f} &≈ \text{softmax}(W_{\tilde{f}}x_t+U_{\tilde{f}}h_{t-1}+b_{\tilde{f}}) \end{aligned}\]则$d_f$应为:
\[d_f = \mathop{\arg\max}_{k} 1_{d_f}[k]\]根据函数的光滑化结论,argmax的光滑近似函数为:
\[\begin{aligned} \mathop{\arg\max}_{k} 1_{d_f}[k] ≈& \sum_{k=1}^n k \times 1_{d_f}[k] \\ =& 1_{d_f}[1] + 2\times 1_{d_f}[2] + \cdots + n \times 1_{d_f}[n] \\ =& (n+1) \times (1_{d_f}[1]+1_{d_f}[2]+\cdots + 1_{d_f}[n]) \\ &- 1_{d_f}[1] - (1_{d_f}[1]+ 1_{d_f}[2]) - \cdots\\ & - (1_{d_f}[1]+1_{d_f}[2]+\cdots + 1_{d_f}[n]) \\ = &n+1-\sum_{k=1}^n \text{cumsum}(1_{d_f}[k]) \\ = &n+1-\sum_{k=1}^n \tilde{f}_t[k] \end{aligned}\]因此可以用以下序列表示输入序列的层级变化:
\[\{d_{f,t}\}_{t=1}^{\text{SequenceLength}} = \{(n+1-\sum_{k=1}^n \tilde{f}_t[k])\}_{t=1}^{\text{SequenceLength}}\]给定输入序列\(\{x_t\}\)和预训练的ON-LSTM,按上式输出对应的层级序列\(\{d_{f,t}\}\),则可使用贪心算法来析出层次结构:
找出层级序列中最大值所在的下标$k$,把输入序列分区为$[x_{t<k},[x_k,x_{t>k}]]$。然后对子序列$x_{t<k}$和$x_{t>k}$重复上述步骤,直到每个子序列长度为$1$。
层级序列的最高层级对应着此处包含的历史信息最少,与前面所有内容的联系最为薄弱,最有可能是一个新的子结构的开始。通过递归处理从而逐渐得到输入序列隐含的嵌套结构。
作者训练了一个三层ON-LSTM,然后使用中间层的$\tilde{f}_t$计算层级,跟标注的句法结构对比准确率比较高:



