SWA:通过随机权重平均寻找更宽的极小值.
深度神经网络通常是通过随机梯度下降算法SGD进行优化的。作者发现使用周期或恒定学习率,并沿着参数的优化轨迹平均多个中间点,能够提高模型的泛化能力,且几乎没有引入额外的计算成本。这种方法称为随机权重平均(stochastic weight averaging, SWA)。
有研究表明以恒定学习率运行SGD相当于在以损失最小值为中心的高斯分布中采样,对于高维空间则相当于在高维高斯分布的球体内采样。由于权重空间是非常高维的,因此大部分采样点集中在球面上;而通过对多次采样结果进行平均能够获得球体内部的解。

此外,训练损失和测试误差不是完全对齐的,这意味着训练集上的最优解不一定是测试集上的最优解。SGD寻找训练误差最小的解,并不一定能泛化到测试误差的小值;
1. 分析SGD轨迹
采用周期性学习率,假设学习率变化周期为$c$,每个周期中学习率从$\alpha_1$线性下降为$\alpha_2$。则第$i$次更新中的学习率为:
\[t(i) = \frac{1}{c} (\text{mod}(i-1,c)+1 ) \\ \alpha(i) = (1-t(i))\alpha_1 + t(i) \alpha_2\]下图展示了循环学习率的设置与相应的泛化误差变化:

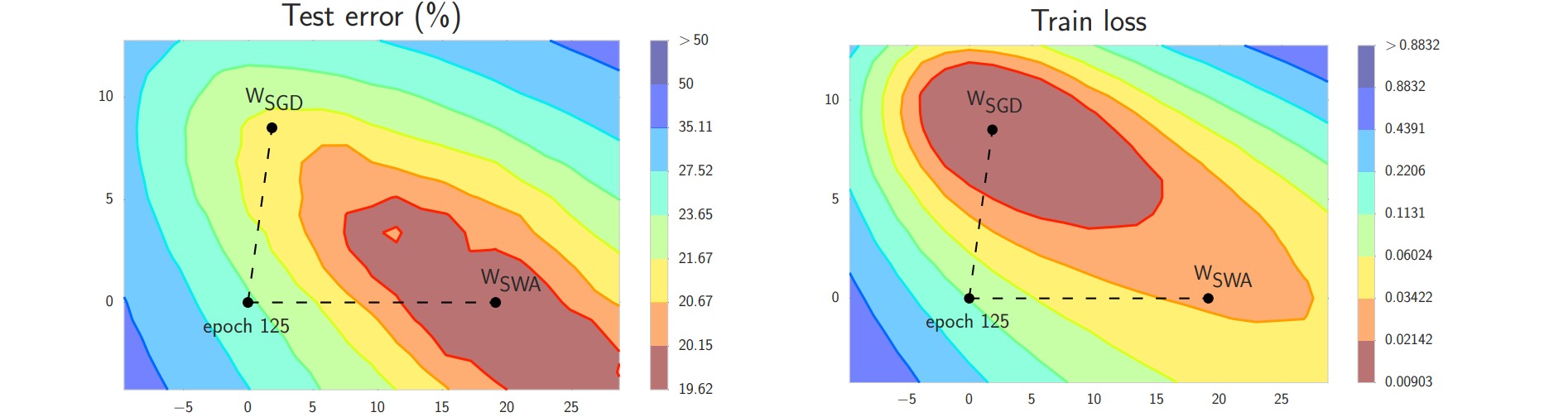
作者在CIFAR-100数据集上训练了ResNet-164模型,并绘制了优化轨迹的初始点、中间点与终点(图中十字点),其余点是这些点的仿射组合:

左边两图是使用周期性学习率的结果;右边两图是使用恒定学习率$t(i) = \alpha_1$的结果。结果表明周期性学习率在探索参数空间时更准确。从图中也能看出训练损失和测试误差没有完全对齐,通过平均优化轨迹能够获得泛化性能更好的点。
2. 随机权重平均 SWA
若学习率变化周期为$c$(对于恒定学习率$c=1$),当训练轮数$i$每完成一个周期时($\text{mod}(i,c)=0$),计算已累积的模型数量:
\[n_{\text{model}} = \frac{i}{c}\]并累积平均权重$w_{\text{SWA}}$:
\[w_{\text{SWA}} = \frac{n_{\text{model}} \cdot w_{\text{SWA}}+w_i}{n_{\text{model}}+1}\]平均权重$w_{\text{SWA}}$在训练时不会用于模型预测,因此也不会记录BatchNorm的激活统计量。因此如果网络存在BatchNorm,则应在训练结束后使用平均权重$w_{\text{SWA}}$对数据额外进行一次前向传播,从而计算每一层神经元的相关统计量。

3. 极小值的宽度
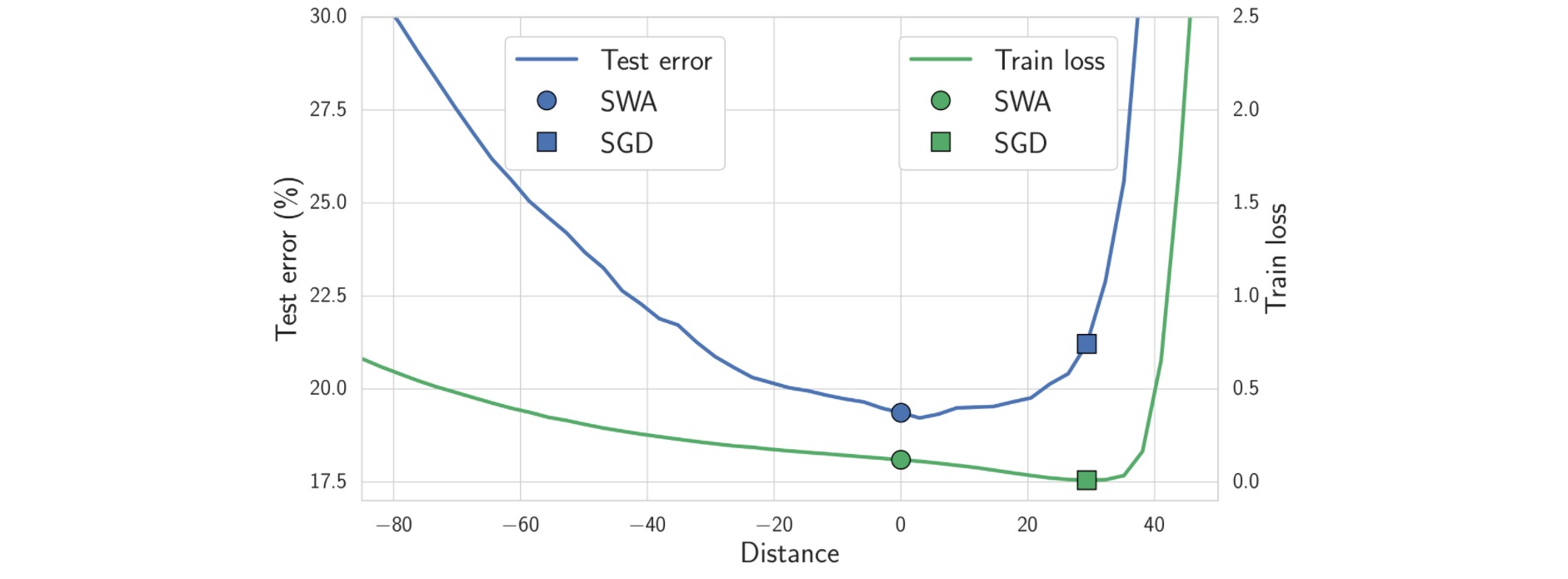
网络收敛到局部极小值有两种情况,平坦极小值和尖锐极小值。由于训练损失和测试误差不完全对齐,只有当收敛到较宽的平坦极小值时,才能在小扰动下仍然保持近似最优。

作者以极小值$w_{\text{SWA}}$和$w_{\text{SGD}}$为中心,沿不同距离采样了参数点,并计算这些参数点对应的训练损失和测试误差。结果表明随着采样距离的增加,SWA方法始终保持较低的误差,即收敛到更平坦的极小值。

4. 实验分析
作者给出了不同方法对应的实验结果:



