权重激励:卷积神经网络中的内部注意力机制.
权重激励(Weight Excitation)是一种在训练阶段判别卷积神经网络权重的重要性,并对重要权重赋予更多注意力的机制。
为探索权重的重要性,作者进行了权重影响的系统性分析(通过将权重置零)。作者研究了关于权重的两种特性:幅值和位置。幅值重要性体现在权重的每一个元素幅值;位置重要性体现在不同的权重通道。为更好说明两者的重要性,作者采用ImageNet数据集上预训练ResNet50进行相应数据分析。

1. Magnitude-based weight excitation
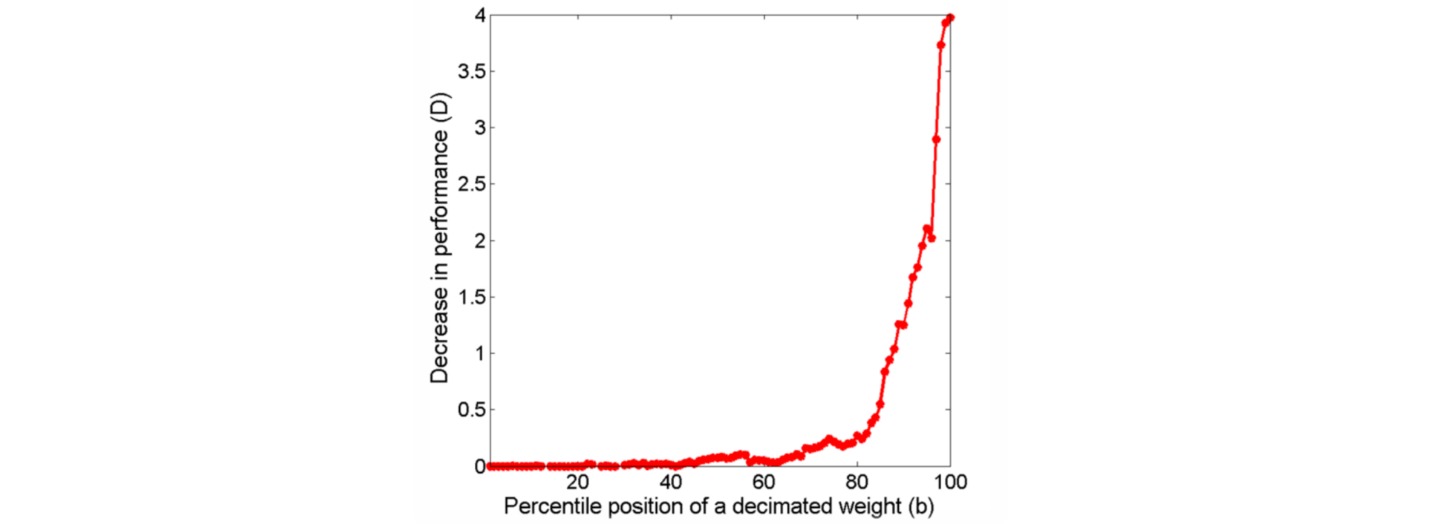
为探索权重幅值的重要性,通过如下流程进行了分析:对于每个卷积权重按照绝对值进行升序排序;将不同百分位的权重置零并记录模型性能下降情况。结果表明把更高百分位的权重(即权重幅值更大)置零导致的性能下降更严重,这也就说明了权重的重要性随幅值变大而变大。
为了调整权重幅值的重要性,设计了一种激活函数,以权重$w$为输入,并赋予其不同的重要性注意力:
\[w_{MWE} = M_A \times 0.5 \times \ln \frac{1+w/M_A}{1-w/M_A}\]其中$M_A=(1+\epsilon_A)\times M$,$M$是权重的最大幅值,$0 <\epsilon_A <0.2$是一个超参数。此时权重的梯度变为:
\[\nabla_w = M_A^2/(M_A^2-w^2)\times \nabla_{w_{MWE}}\]
2. Location-based weight excitation
为探索权重位置的重要性,选择$N_1$个输出通道;对每个所选择的输出通道,选择$N_2$个输入通道;将上述所选择的输入通道对应的权重置零并记录模型性能下降情况。结果表明浅层的下降波动更大,深层的下降波动较小,这也就意味着不同位置的权重重要性是不同的,且浅层的权重重要性差异更明显。

卷积权重的重要性会随位置而发生变化,因此对于维度为$c_{out} \times c_{in} \times k \times k$的权重,每个$k \times k$权重的重要性是可变的。直接生成$c_{out} \times c_{in}$大小的注意力图具有较大参数量,因此通过一个注意力子网络把$c_{in} \times k \times k$的权重作为输入生成$c_{in}$个重要性注意力值,相同的子网络同时处理多路权重进而得到$c_{out} \times c_{in}$大小的注意力图。


