Meta Learning.
元学习（Meta Learning）又叫学会学习（Learning to learn），旨在让机器学会如何去学习。
本文目录：
- 问题的提出
- Benchmarks
- MAML
- Reptile
1. 问题的提出
传统的机器学习问题是给定数据集$D_{train}$，人为选择一个函数$f$，训练该函数解决问题；
元学习是给定数据集$D_{train}$后，训练一个函数$F$，使得该函数$F$能够选择一个合适的函数$f$解决问题。
在元学习中，需要设置训练任务集（training tasks）和测试任务集（testing tasks），必要时还要设置验证任务集（valida tasks）。
对于每一个任务集中的任务，应包括support set（即训练集）和query set（即测试集）。
定义训练任务集一共有$N$个任务，每个任务使用$F$选择的函数$f$训练后，在测试集上的损失函数为$l^n$；则元学习的损失函数为：
\[L(F) = \sum_{n=1}^{N} {l^n}\]则元学习的目标函数为：
\[F^* = argmin_{F} L(F)\]元学习包括但不限于：
- 自动选择网络结构；
- 自动选择参数初始化的值；
- 自动选择参数更新方式。
本文介绍两种自动选择参数初始化的值的方法，MAML和Reptile。
2. Benchmarks
元学习常用的Benchmarks包括：
- Omniglot
Omniglot
- 主页：github
Omniglot数据集包含1623种符号，每种符号包含20个样本。
该数据集可以做few-shot 分类，具体地，实现N-ways K-shot 分类：
每个任务的设置：从数据集中随机采样N个符号的类，每个类包含K个样本。
3. MAML
MAML(Model-Agnostic Meta-Learning)是一种自动选择初始化网络参数的元学习方法，希望能够找到合适的初始化参数，使得不同任务通过该初始化参数进行学习都能收敛到不错的结果。由于选择的是网络参数的初始化值，要求不同任务使用的网络结构是相同的。
记网络的初始化参数为$Φ$，每一个任务从$Φ$开始训练，在support set上训练后的参数为$\hat{θ}$，在query set上的损失为$l(\hat{θ})$，则元学习的损失函数为：
\[L(Φ) = \sum_{n=1}^{N} {l^n(\hat{θ}^n)}\]可以使用梯度下降法更新参数$Φ$:
\[Φ = Φ - η▽_ΦL(Φ)\]该模型并不在意初始化参数为$Φ$在训练任务上最终的表现如何，而是用$Φ$训练出的参数$\hat{θ}$使网络表现如何：
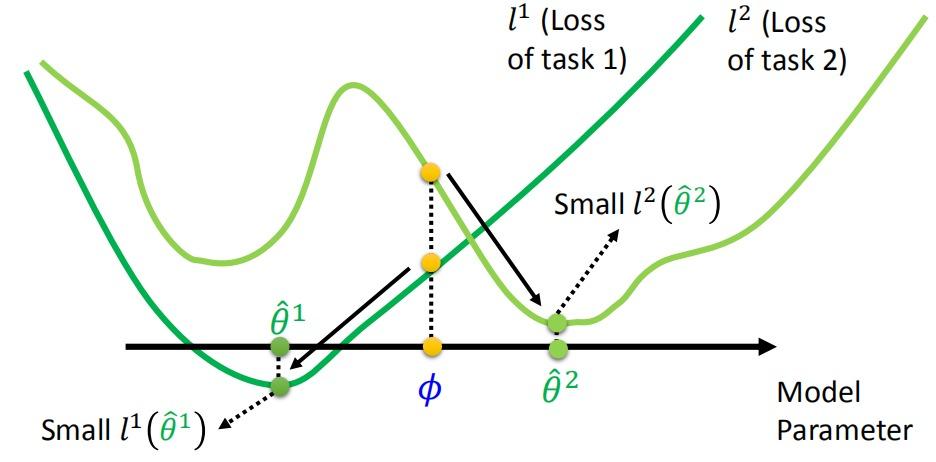
与模型预训练的区别
模型预训练（model pre-training）是一种经常应用在迁移学习中的方法，希望能够通过学习找到合适的参数在这些任务上都表现出较好的结果。
预训练定义的损失函数是：
\[L(Φ) = \sum_{n=1}^{N} {l^n(\hat{Φ})}\]模型预训练也使用梯度下降更新参数：
在任务$m$上更新得到参数$\hat{θ}^m$，于是将初始化参数更新为$Φ^1$（由于学习率不同，两组参数不相同）；在任务$n$上继续更新…直至训练结束。
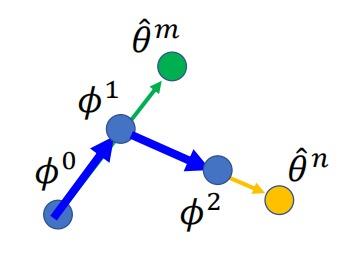
模型预训练寻找在所有训练任务上都表现较好的初始化参数$Φ$，但并不能保证该参数对其它任务训练会有帮助：
MAML的实际实现
\[L(Φ) = \sum_{n=1}^{N} {l^n(\hat{θ}^n)}\] \[Φ = Φ - η▽_ΦL(Φ)\]MAML在实现时，对于每个任务，仅进行一次梯度更新，即：
\[\hat{θ} = Φ - ε▽_Φl(Φ)\]计算梯度：
\[▽_ΦL(Φ) = ▽_Φ \sum_{n=1}^{N} {l^n(\hat{θ}^n)} = \sum_{n=1}^{N} {▽_Φl^n(\hat{θ}^n)}\]其中：
\[▽_Φl(\hat{θ}) = \begin{bmatrix} \frac{\partial l(\hat{θ})}{\partial Φ_1} \\ ... \\ \frac{\partial l(\hat{θ})}{\partial Φ_i} \\ ... \\ \end{bmatrix}\]由链式法则：
\[\frac{\partial l(\hat{θ})}{\partial Φ_i} = \sum_{j}^{} {\frac{\partial l(\hat{θ})}{\partial \hat{θ}_j} \frac{\partial \hat{θ}_j}{\partial Φ_i}}\]由\(\hat{θ}_j = Φ_j - ε\frac{\partial l(Φ)}{\partial Φ_j}\)可得：
\[\frac{\partial \hat{θ}_j}{\partial Φ_i} = \begin{cases} - ε\frac{\partial^2 l(Φ)}{\partial Φ_j \partial Φ_i}, & i≠j \\ 1-ε \frac{\partial^2 l(Φ)}{\partial Φ_j \partial Φ_i} , & i=j \end{cases}\]忽略二阶导数，得：
\[\frac{\partial \hat{θ}_j}{\partial Φ_i} ≈ \begin{cases} 0, & i≠j \\ 1, & i=j \end{cases}\]则得下列近似：
\[\frac{\partial l(\hat{θ})}{\partial Φ_i} = \sum_{j}^{} {\frac{\partial l(\hat{θ})}{\partial \hat{θ}_j} \frac{\partial \hat{θ}_j}{\partial Φ_i}} ≈ \frac{\partial l(\hat{θ})}{\partial \hat{θ}_i}\]可得近似梯度：
\[▽_Φl(\hat{θ}) = \begin{bmatrix} \frac{\partial l(\hat{θ})}{\partial Φ_1} \\ ... \\ \frac{\partial l(\hat{θ})}{\partial Φ_i} \\ ... \\ \end{bmatrix} ≈ \begin{bmatrix} \frac{\partial l(\hat{θ})}{\partial \hat{θ}_1} \\ ... \\ \frac{\partial l(\hat{θ})}{\partial \hat{θ}_i} \\ ... \\ \end{bmatrix} = ▽_{\hat{θ}}l(\hat{θ})\]即用每一个任务中$\hat{θ}$的梯度方向作为参数$Φ$的更新方向：
4. Raptile
Reptile在每个任务中进行多次梯度更新，并将参数的初始指向终止方向作为初始化参数的更新方向：
Reptile可近似的看作MAML和模型预训练的结合：
