Hopfield Neural Networks.
本文目录:
- Hopfield神经网络
- 能量函数
- 联想记忆
1. Hopfield神经网络
Hopfield神经网络(Hopfield Neural Network)是一种循环神经网络模型,是一种相互连接型的网络,也是一种单层反馈神经网络。
Hopfield网络中,每一个神经元都和除自己外的所有神经元相互连接,如下图所示:

本文主要关注离散型Hopfield网络,即每一个神经元的取值是离散的:\(\{0,1\}\)。
Hopfield网络中不同神经元之间连接权重是对称的,若记$w_{ij}$为神经元$i$和$j$之间的连接权重,则满足:
\[w_{ii} = 0\] \[w_{ij} = w_{ji}, \quad i ≠ j\]Hopfield网络的更新分为异步和同步两种方式:
- 异步(串行)更新是指每次更新一个神经元,神经元的更新顺序可以是随机或事先固定的;
- 同步(并行)更新是指一次更新所有的神经元,需要有一个时钟来进行同步。
假设Hopfield网络有$N$个神经元,第$i$个神经元的更新规则如下:
\[x_i^{(t+1)} = \begin{cases} 1, & \text {if $\sum_{n=1}^{N} {w_{in}x_n^{(t)}+b_i} ≥ 0$} \\ 0, & \text{otherwise} \end{cases}\]其中$w_{in}$为神经元$i$和$n$之间的连接权重,$b_i$为神经元$i$的偏置。
一种简单的连接权重学习方式是:
\[w_{ij} = \frac{1}{M} \sum_{m=1}^{M} {x_i^mx_j^m}\]其中$M$表示总共有$M$个数据。
这种学习规则和人脑的学习方式Hebbian法则类似:如果两个神经元经常同时激活,则它们之间的连接加强;如果两个神经元经常不同时激活,则连接消失。
2. 能量函数
Hopfield网络的能量函数$E$定义为:
\[E = -\frac{1}{2}\sum_{i,j}^{} {w_{ij}x_ix_j} - \sum_{i}^{} {b_ix_i}\]能量函数可以作为Hopfield网络训练的终止判断条件。
根据定义的更新规则,能量函数是非递增的。即随时间的不断增加而逐渐减小,直到网络达到稳定状态为止。
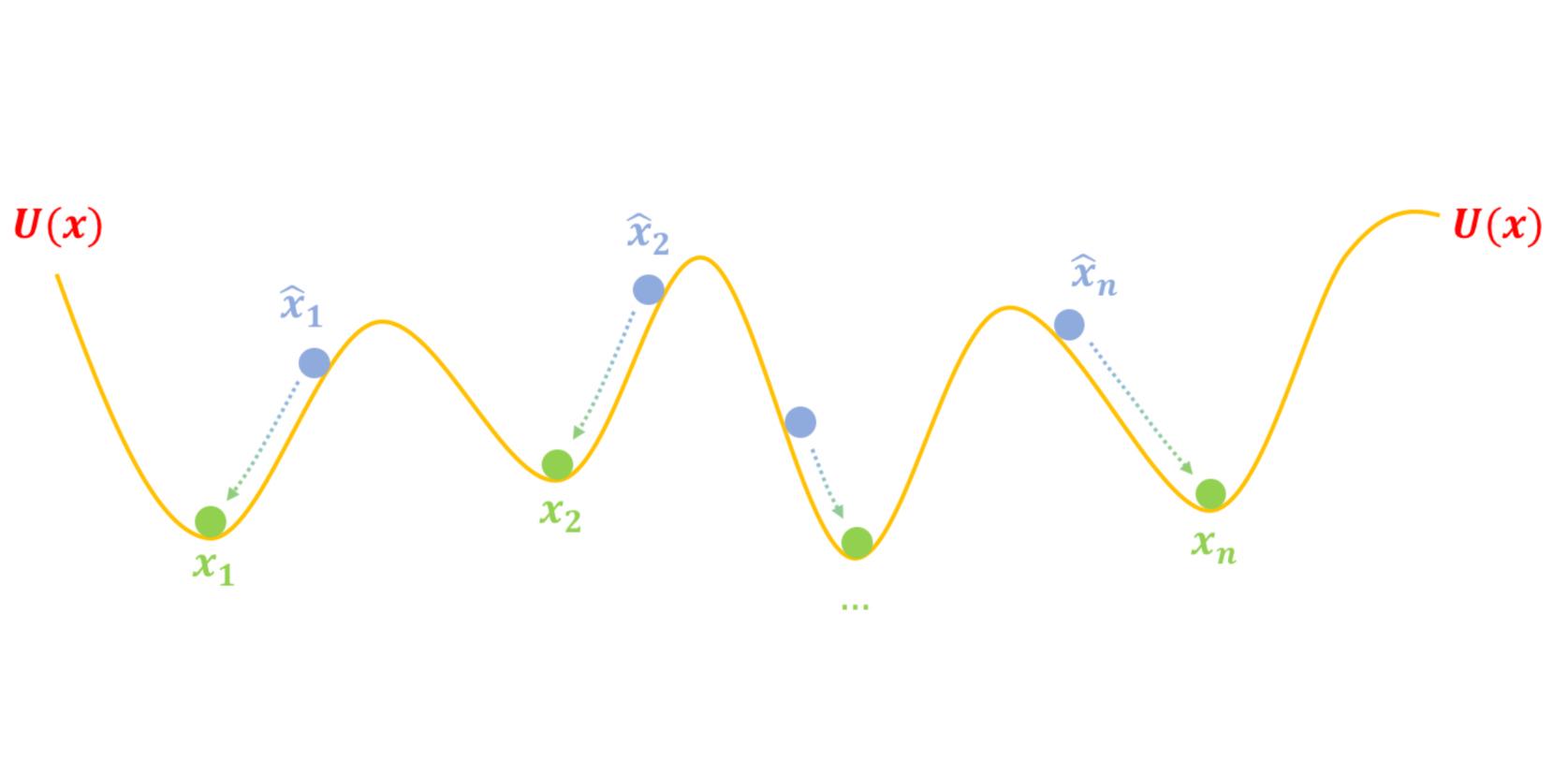
网络最终到达的稳定状态称为吸引点(Attractor)。吸引点是能量函数的一系列局部极小点。
下图给出了Hopfield网络的能量函数。红线为网络能量的演化方向,蓝点为吸引点。

3. 联想记忆
联想记忆(Associative Memory)是指当输入模式为某种状态时,输出端要给出与之相应的输出模式。可以通过神经网络的动态演化来进行联想。
- 自联想记忆:输入的模式和输出的模式在同一空间。可以作为自编码器。
- 异联想记忆:输入的模式和输出的模式不在同一空间。可以作为分类器。
Hopfield网络存在有限的吸引点,可以看作网络中存储的模式(Pattern)。将网络输入作为起始状态,随时间收敛到吸引点上的过程作为检索过程。
Hopfield网络中可以作为有效稳定点的状态数量就是其存储容量。对于具有$N$个神经元的Hopfield网络,其存储容量是$0.14N$。
通过改进学习算法,Hopfield网络的最大容量可以达到$O(N)$。
如果允许高阶(阶数为$𝐾$)连接,比如三个神经元连接关系,其稳定存储的最大容量为$O(N^{K-1})$。
当需要记忆的模式之间的较为相似、或者需要记忆的模式太多时,Hopfield神经网络就不能正确地辨别模式。这种相互干扰、不能准确记忆的情况称为串扰(crosstalk)。
解决串扰的方法:
- 模式正交化;
- 玻尔兹曼机。